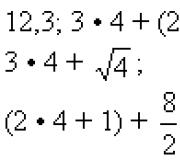Relativ feil online kalkulator. Relativ feil

3.1 Aritmetisk gjennomsnittsfeil. Som nevnt tidligere, kan målinger i utgangspunktet ikke være helt nøyaktige. Derfor, under målingen, oppstår problemet med å bestemme intervallet der den sanne verdien av den målte mengden er mest sannsynlig å bli funnet. Et slikt intervall er angitt som en absolutt målefeil.

Dersom vi antar at grove feil i målingene elimineres, og systematiske feil minimeres ved nøye justering av instrumentene og hele installasjonen og ikke er avgjørende, så vil måleresultatene i hovedsak kun inneholde tilfeldige feil, som er fortegnsvekslende verdier. Derfor, hvis flere gjentatte målinger av samme mengde utføres, er den mest sannsynlige verdien av den målte mengden dens aritmetiske gjennomsnitt:

Gjennomsnittlig absolutt feil kalles det aritmetiske gjennomsnittet av absolutte feilmoduler for individuelle målinger:

Den siste ulikheten skrives vanligvis som det endelige resultatet av målingen som følger:

(5)

hvor den absolutte feilen a cf skal beregnes (avrundes) til innenfor ett eller to signifikante tall. Den absolutte feilen viser hvilket tegn på tallet som inneholder unøyaktigheter, derfor i uttrykket for en vi la alle de riktige tallene og en tvilsom. Det vil si at gjennomsnittsverdien og gjennomsnittsfeilen til den målte verdien skal beregnes til samme siffer av samme siffer. For eksempel: g = (9,78 ± 0,24) m/s 2.

Relativ feil. Den absolutte feilen bestemmer intervallet for de mest sannsynlige verdiene av den målte verdien, men karakteriserer ikke graden av nøyaktighet av målingene. For eksempel avstanden mellom bosetninger, målt med en nøyaktighet på flere meter, kan tilskrives svært nøyaktige mål, mens målingen av tråddiameteren med en nøyaktighet på 1 mm, i de fleste tilfeller vil være et svært omtrentlig mål.

Graden av nøyaktighet av de utførte målingene er preget av den relative feilen.

Midten relativ feil eller ganske enkelt relativ målefeil er forholdet mellom den gjennomsnittlige absolutte målefeilen og gjennomsnittsverdien av den målte mengden:

Den relative feilen er en dimensjonsløs størrelse og uttrykkes vanligvis som en prosentandel.

3.2 Metodefeil eller instrumentell feil. Den aritmetiske middelverdien til den målte verdien er jo nærmere den sanne, jo flere målinger tas, mens den absolutte målefeilen med en økning i antallet tenderer til verdien som bestemmes av målemetoden og tekniske spesifikasjoner enheter som brukes.

Metodefeil eller instrumentfeilen kan beregnes fra en enkelt måling, med kjennskap til instrumentets nøyaktighetsklasse eller andre data teknisk pass instrument, som indikerer enten nøyaktighetsklassen til instrumentet, eller dets absolutte eller relative målefeil.

Nøyaktighetsklasse instrument uttrykker i prosent det nominelle relativ feil enhet, det vil si den relative målefeilen når den målte verdien er lik grenseverdien for denne enheten

Den absolutte feilen til enheten avhenger ikke av verdien av den målte mengden.

Relativ instrumentfeil (per definisjon):

(10)

hvorfra det kan sees at den relative instrumentelle feilen er den minste, den nærmere mening målt verdi til målegrensen for denne enheten. Derfor anbefales det å velge enheter slik at den målte verdien er 60-90 % av verdien som enheten er designet for. Når man arbeider med multi-limit instrumenter bør man også tilstrebe at avlesningen foretas i andre halvdel av skalaen.

Når du arbeider med enkle instrumenter (linjal, beger, etc.), hvis nøyaktighet og feilklasser ikke bestemmes av de tekniske egenskapene, tas den absolutte feilen for direkte målinger halv skaladeling av denne enheten. (Delingsprisen er verdien av den målte mengden når instrumentet leser i én divisjon).

Instrumentell feil ved indirekte målinger kan beregnes ved hjelp av tilnærmingsreglene. Beregningen av feilen ved indirekte målinger er basert på to forhold (forutsetninger):

1. Absolutte målefeil er alltid svært små sammenlignet med de målte verdiene. Derfor kan absolutte feil (i teorien) betraktes som infinitesimale økninger av målte mengder, og de kan erstattes av de tilsvarende differensialene.

2. Hvis en fysisk størrelse som bestemmes indirekte er en funksjon av en eller flere direkte målte størrelser, så er den absolutte feilen til funksjonen, på grunn av infinitesimale inkrementer, også en infinitesimal størrelse.

Under disse forutsetningene kan de absolutte og relative feilene beregnes ved å bruke velkjente uttrykk fra teorien om differensialregning av funksjoner til mange variabler:

	(11)
	(12)

De absolutte feilene ved direkte målinger kan ha pluss- eller minustegn, men hvilket er ukjent. Derfor, når man bestemmer feilene, vurderes det mest ugunstige tilfellet, når feilene ved direkte målinger av individuelle mengder har samme tegn, det vil si at den absolutte feilen har en maksimal verdi. Derfor, når du beregner inkrementene til funksjonen f(x 1 ,x 2 ,…,х n) i henhold til formlene (11) og (12), må partielle økninger legges til i absolutt verdi. Dermed bruker tilnærmingen Dх i ≈ dx i , og uttrykk (11) og (12), for infinitesimale inkrementer Ja kan skrives:

	(13)
	(14)

Her: en - indirekte målt fysisk mengde, det vil si bestemt av beregningsformelen, Ja er den absolutte feilen for målingen, x 1, x 2, ... x n; Dх 1, Dx 2 ,..., Dх n ,- henholdsvis fysiske mengder direkte målinger og deres absolutte feil.

Således: a) den absolutte feilen til den indirekte målemetoden er lik summen av modulene til produktene av partielle derivater av målefunksjonen og de tilsvarende absolutte feilene til direkte målinger; b) den relative feilen til den indirekte målemetoden er lik summen av modulene til differensialene fra logaritmen naturlig funksjon måling bestemt av beregningsformelen.

Uttrykk (13) og (14) gjør det mulig å beregne de absolutte og relative feilene fra en enkelt måling. Merk at for å redusere beregningene ved å bruke de angitte formlene, er det tilstrekkelig å beregne en av feilene (absolutt eller relativ), og beregne den andre ved å bruke et enkelt forhold mellom dem:

(15)

I praksis brukes formel (13) oftere, siden når man tar logaritmen til beregningsformelen, konverteres produktene av forskjellige mengder til de tilsvarende summene, og kraften og eksponentialfunksjonene konverteres til produkter, noe som i stor grad forenkler prosessen av differensiering.

For praktisk veiledning om beregning av usikkerheten til en indirekte målemetode kan følgende regel brukes:

For å beregne den relative feilen til den indirekte målemetoden, trenger du:

1. Bestem de absolutte feilene (instrumentelle eller gjennomsnittlige) for direkte målinger.

2. Ta logaritmen til den beregnede (fungerende) formelen.

3. Ved å ta verdiene til direkte målinger som uavhengige variabler, finn den totale differensialen fra det resulterende uttrykket.

4. Legg sammen alle partielle differensialer i absolutt verdi, og erstatt de variable differensialene i dem med de tilsvarende absolutte feilene for direkte målinger.

For eksempel beregnes tettheten til en sylindrisk kropp ved hjelp av formelen:

(16)

hvor m, D, h - målte mengder.

Vi får formelen for å beregne feilene.

1. Basert på utstyret som brukes, bestemmer vi de absolutte feilene ved måling av sylinderens masse, diameter og høyde (∆m, ∆D, ∆h henholdsvis).

2. Vi logaritmer uttrykk (16):

3. Differensiere:

4. Ved å erstatte differensialen til uavhengige variabler med absolutte feil og legge til modulene med partielle inkrementer, får vi:

5. Bruke numeriske verdier m, D, h, D, m, h, vi forventer E.

6. Beregn den absolutte feilen

hvor r beregnet ved formel (16).

Vi inviterer deg til å se selv at i tilfelle av en hul sylinder eller rør med en indre diameter D1 og utvendig diameter D2

Det er nødvendig å ty til beregningen av feilen i målemetoden (direkte eller indirekte) i tilfeller der flere målinger enten er umulige å utføre under samme forhold, eller de tar lang tid.

Hvis bestemmelsen av målefeilen er en grunnleggende oppgave, utføres vanligvis målinger gjentatte ganger og både den aritmetiske gjennomsnittsfeilen og metodefeilen (instrumentfeilen) beregnes. I det endelige resultatet, angi den største av dem.

Om nøyaktigheten av beregninger

Resultatfeilen bestemmes ikke bare av målingsunøyaktigheter, men også av beregningsunøyaktigheter. Beregninger må utføres slik at feilen deres er en størrelsesorden mindre enn feilen til måleresultatet. For å gjøre dette, husk reglene matematisk handling med nære tall.

Måleresultater er omtrentlige tall. I et omtrentlig tall må alle tall være riktige. Det siste riktige sifferet i et omtrentlig tall er et slikt siffer, feilen som ikke overstiger én enhet av sifferet. Alle sifre fra 1 til 9 og 0, hvis det er i midten eller på slutten av tallet, kalles signifikante. I tallet 2330 er det 4 signifikante sifre, og i tallet 6,1 × 10 2 - bare to, i tallet 0,0503 - tre, siden nullene til venstre for de fem er ubetydelige. Å skrive tallet 2,39 betyr at alle tegn opp til sekundet etter desimaltegnet er riktige, og å skrive 1,2800 betyr at det tredje og fjerde tegnet også er sant. I tallet 1.90 er det tre signifikante sifre, og dette betyr at vi ved måling tok hensyn til ikke bare enheter, men også tideler og hundredeler, og i tallet 1.9 - bare to signifikante sifre, og dette betyr at vi tok hensyn til heltall og tideler. og nøyaktigheten er dette tallet 10 ganger mindre.

Tallavrundingsregler

Ved avrunding er det kun de riktige tegnene igjen, resten forkastes.

1. Avrunding oppnås ved ganske enkelt å forkaste sifrene hvis det første av de forkastede sifrene er mindre enn 5.

2. Hvis det første av de forkastede sifrene er større enn 5, økes det siste sifferet med ett. Det siste sifferet økes også når det første av de forkastede sifrene er 5 etterfulgt av ett eller flere sifre som ikke er null.

For eksempel vil ulike avrundinger av tallet 35.856 være: 35.9; 36.

3. Hvis det forkastede sifferet er 5, og det ikke er noen signifikante sifre bak det, utføres avrunding til nærmeste partall, det vil si at det siste sifferet som skal lagres forblir uendret hvis det er partall og øker med én hvis det er merkelig.

For eksempel rundes 0,435 opp til 0,44; 0,365 rundes opp til 0,36.

Absolutte og relative feil

Vi må forholde oss til omtrentlige tall når vi beregner verdiene til noen funksjoner, eller når vi måler og behandler fysiske mengder oppnådd som et resultat av eksperimenter. I begge tilfeller må du være i stand til å skrive ned verdiene til omtrentlige tall og feilen deres.

Omtrentlig antall en kalles et tall som avviker litt fra det eksakte tallet MEN og erstatter sistnevnte i beregninger. Hvis det er kjent det en< А , deretter en kalles den omtrentlige verdien av tallet MEN av mangel; hvis a > a,- da i overkant. Hvis en en er den omtrentlige verdien av tallet MEN, så skriver de a ≈ A.

Under feil eller feil MEN omtrentlig antall en vanligvis forstått som forskjellen mellom det tilsvarende nøyaktige tallet MEN og gitt omtrentlige, dvs.

For å få det nøyaktige tallet MEN, må du legge til feilen til den omtrentlige verdien av tallet, dvs.

I mange tilfeller er tegnet på feilen ukjent. Da er det lurt å bruke den absolutte feilen til det omtrentlige tallet

Fra oppføringen ovenfor følger det at den absolutte feilen til det omtrentlige tallet en kalles modulen for differansen mellom det tilsvarende nøyaktige tallet MEN og dens omtrentlige verdi en, dvs.

Nøyaktig antall MEN oftest er det ukjent, så det er ikke mulig å finne en feil eller en absolutt feil. I dette tilfellet, i stedet for en ukjent teoretisk feil, er det nyttig å introdusere det øvre estimatet, den såkalte begrensende absolutte feilen.

Under den begrensende absolutte feilen til det omtrentlige tallet en ethvert tall forstås som ikke er mindre enn den absolutte feilen til dette tallet, dvs.

Hvis i den siste oppføringen i stedet for å bruke formelen (1.1), så kan vi skrive

(1.2)

Det følger at det nøyaktige antallet MEN inneholdt innenfor grensene

Derfor er forskjellen en tilnærming av tallet A ved mangelen, og - talltilnærming MEN i overkant. I dette tilfellet, for korthets skyld, bruker vi notasjonen

Det er klart at den begrensende absolutte feilen er definert tvetydig: hvis et visst tall er den begrensende absolutte feilen, så er et hvilket som helst større enn et positivt tall også den begrensende absolutte feilen. I praksis prøver de å velge det minste og enkleste mulige tallet, og tilfredsstiller ulikheten (1.2).

For eksempel, hvis vi som et resultat av målingen fikk lengden på segmentet l\u003d 210 cm ± 0,5 cm, så her den begrensende absolutte feilen = 0,5 cm, og den nøyaktige verdien l segmentet er innelukket innenfor grensene på 209,5 cm ≤l≤ 210,5 cm.

Den absolutte feilen er ikke tilstrekkelig til å karakterisere nøyaktigheten til en måling eller beregning. Så, for eksempel, hvis når du måler lengden på to stenger, oppnås resultatene l 1= 95,6 cm ± 0,1 cm og l 2= 8,3 ± 0,1 cm, så, til tross for sammenfallet av de begrensende absolutte feilene, er nøyaktigheten av den første målingen høyere enn den andre. Dette viser at for nøyaktigheten av målingene er det viktigere, ikke den absolutte, men den relative feilen, som avhenger av verdiene til de målte mengdene.

Relativ feil δ omtrentlig antall en er forholdet mellom den absolutte feilen til dette tallet og modulen til det tilsvarende nøyaktige tallet MEN, de.

På samme måte som den begrensende absolutte feilen, brukes definisjonen også for den begrensende relative feilen. Den begrensende relative feilen til dette omtrentlige tallet en ethvert tall kalles som ikke er mindre enn den relative feilen til dette tallet

de. hvor det følger

Altså, for den begrensende absolutte feilen til tallet en kan godtas

Siden i praksis A≈a, så i stedet for formel (1.3) bruker man ofte formelen

1.2 Desimalnotasjon av omtrentlige tall

Noe positivt desimaltall og kan representeres som en endelig eller uendelig brøk

hvor er desimalsifrene i tallet en( = 0,1,2,...,9), og det høyeste sifferet a m- antall sifre i heltallsdelen av tallet en, a n- antall sifre i posten for brøkdelen av nummeret en. For eksempel:

5214.73... = 5 10 3 + 2 10 2 + 1 10 1 + 4 10 0 +7 10 -1 + 3 10 -2 ... (1,5)

Hvert siffer på et bestemt sted i et tall en skrevet på formen (1.4) har sin egen vekt. Så tallet i utgangspunktet (dvs.) veier 10 m, på den andre - 10 m-1 osv.

I praksis bruker vi vanligvis ikke notasjonen i formen (1.4), men bruker den forkortede notasjonen av tall i form av en sekvens av koeffisienter med tilsvarende potenser av 10. dette tallet i potenser av 10.

I praksis må man hovedsakelig forholde seg til omtrentlige tall i form av endelige desimalbrøker. For en korrekt sammenligning av ulike beregningsmessige og eksperimentelle resultater, introduseres konseptet betydelig siffer i resultatrekorden. Alle lagret desimalverdier ( i = m,m- 1,…, m-n+ 1) annet enn null, og null hvis det er mellom signifikante sifre eller er en representant for et lagret desimalsted på slutten av tallet kalles signifikante sifre i det omtrentlige tallet en. I dette tilfellet er nullene knyttet til faktoren 10 n er ikke vesentlige.

Med posisjonsbetegnelsen til nummeret en i desimaltallsystemet må du noen ganger legge inn ekstra nuller på begynnelsen eller slutten av tallet. For eksempel,

en= 7 10 -3 + 0 10 -4 + 1 10 -5 + 0 10 -6 = 0,00 7010

b= 2 10 9 + 0 10 8 + 0 10 7 + 3 10 6 + 0 10 5 = 2003000000.

Slike nuller (understreket i eksemplene) regnes ikke som signifikante sifre.

Det signifikante sifferet til et omtrentlig tall er et hvilket som helst siffer i desimalrepresentasjonen som er forskjellig fra null.,samt null hvis den er inneholdt mellom signifikante sifre eller er en representant for en lagret desimal. Alle andre nuller som er en del av det omtrentlige tallet og kun tjener til å angi dets desimaler, regnes ikke som signifikante tall.

For eksempel, i tallet 0,002080, er de tre første nullene ikke signifikante sifre, siden de bare tjener til å etablere desimalplassene til andre sifre. De resterende to nullene er signifikante sifre, siden den første av dem er mellom de signifikante sifrene 2 og 8, og den andre indikerer at desimalplassen 10 -6 er lagret i det omtrentlige tallet. Hvis det siste sifferet i et gitt tall 0,002080 ikke er signifikant, bør dette tallet skrives som 0,00208. Fra dette synspunktet er tallene 0,002080 og 0,00208 ikke like, siden den første av dem inneholder fire signifikante sifre, og den andre bare tre.

I tillegg til begrepet en betydelig figur, begrepet riktig antall. Det skal bemerkes at dette konseptet finnes i to definisjoner - i smal og vid forstand.

Definisjon(i vid forstand) . De sier det n de første signifikante sifrene i tallet (teller fra venstre til høyre) er trofast i vid mening, hvis den absolutte feilen til dette tallet ikke overstiger én (vekt) n- varm utflod. (Forklaring: 1 10 1 - her er vekt 1 lik 10; 1 10 0 - her er vekt 1 lik 1; 1 10 -1 - her er vekt 1 lik 0,1; 1 10 -2 - her er vekt 1 lik til 0,01 og t.d.).

Definisjon(i snever forstand). De sier det n første signifikante sifre i et omtrentlig tall er korrekte hvis den absolutte feilen til dette tallet ikke overskrider halv enheter (vekt) n- varm utflod. (Forklaring: 1 10 1 - her er vekten av halv 1 5; 1 10 0 - her er vekten av halv 1 0,5; 1 10 -1 - 0,05 osv.).

For eksempel i et omtrentlig antall Ut fra den første definisjonen er de signifikante tallene 3,4 og 5 korrekte i vid forstand, og tallet 6 er tvilsomt. Basert på den andre definisjonen er de signifikante tallene 3 og 4 riktige i snever forstand, og tallene 5 og 6 er tvilsomme. Det er viktig å understreke at nøyaktigheten til et omtrentlig tall ikke avhenger av antall signifikante sifre, men av antallet riktige signifikante sifre.

Både i teoretisk resonnement og i praktiske applikasjoner definisjonen av riktig figur i snever forstand finner mer anvendelse.

Derfor, hvis for et omtrentlig tall a, erstatter tallet MEN, det er kjent at

(1.6)

deretter, per definisjon, den første n tall dette tallet er riktig.

For eksempel for det nøyaktige antallet MEN= 35,97 tall en= 36,00 er en tilnærming med tre gyldige sifre. Følgende resonnement fører til dette resultatet. Siden den absolutte feilen til vårt omtrentlige tall er 0,03, må det per definisjon tilfredsstille betingelsen

(1.7)

I vårt omtrentlige tall 36.00 er 3 det første signifikante sifferet (dvs. ), så m= 1. Derfor er det åpenbart at betingelse (1.7) vil være oppfylt for n = 3.

Vanligvis tatt når desimalnotasjon av et omtrentlig tall skriv kun riktige tall. Hvis det er kjent at dette omtrentlige tallet er skrevet riktig, kan den maksimale absolutte feilen bestemmes fra posten. Det er med korrekt registrering at den absolutte feilen ikke overstiger halvparten av det minst signifikante sifferet som følger det siste riktige sifferet (eller halvparten av enheten til det siste riktige sifferet, som er det samme)

For eksempel gitt omtrentlige tall skrevet riktig: a = 3,8; b= 0,0283; c = 4260. I henhold til definisjonen vil de begrensende absolutte feilene for disse tallene være: = 0,05; = 0,00005; = 0,5.

Fysiske mengder er preget av konseptet "feilnøyaktighet". Det er et ordtak som sier at ved å ta målinger kan man komme til kunnskap. Så det vil være mulig å finne ut hva som er høyden på huset eller lengden på gaten, som mange andre.

Introduksjon

La oss forstå betydningen av begrepet «måle verdien». Måleprosessen er å sammenligne den med homogene mengder, som tas som en enhet.

Liter brukes til å bestemme volum, gram brukes til å beregne masse. For å gjøre det lettere å gjøre beregninger, introduserte vi SI-systemet internasjonal klassifisering enheter.

For å måle lengden på myren i meter, masse - kilogram, volum - kubikkliter, tid - sekunder, hastighet - meter per sekund.

Ved beregning av fysiske mengder er det ikke alltid nødvendig å bruke tradisjonell måte, er det nok å bruke beregningen ved å bruke formelen. For eksempel, for å beregne indikatorer som gjennomsnittshastighet, må du dele den tilbakelagte avstanden med tiden du har brukt på veien. Slik beregnes gjennomsnittshastigheten.

Ved å bruke måleenheter som er ti, hundre, tusen ganger høyere enn indikatorene for de aksepterte måleenhetene, kalles de multipler.

Navnet på hvert prefiks tilsvarer multiplikatornummeret:

Deca.
Hecto.
Kilo.
Mega.
Giga.
Tera.

I fysisk vitenskap brukes en potens på 10 for å skrive slike faktorer, for eksempel er en million angitt som 10 6 .

I en enkel linjal har lengden en måleenhet - en centimeter. Den er 100 ganger mindre enn en meter. En 15 cm linjal er 0,15 m lang.

En linjal er den enkleste typen måleinstrument for å måle lengde. Mer komplekse enheter er representert av et termometer - slik at et hygrometer - for å bestemme fuktighet, et amperemeter - for å måle kraftnivået som en elektrisk strøm forplanter seg med.

Hvor nøyaktige vil målingene være?

Ta en linjal og en enkel blyant. Vår oppgave er å måle lengden på dette brevpapiret.

Først må du finne ut hva som er divisjonsprisen som er angitt på skalaen måleinstrument. På de to divisjonene, som er de nærmeste strekene på skalaen, skrives tall, for eksempel "1" og "2".

Det er nødvendig å beregne hvor mange divisjoner som er innelukket i intervallet til disse tallene. Teller du riktig får du "10". Trekk fra tallet som er større, tallet som vil være mindre, og del på tallet som utgjør divisjonene mellom sifrene:

(2-1)/10 = 0,1 (cm)

Så vi bestemmer at prisen som bestemmer inndelingen av skrivesaker er tallet 0,1 cm eller 1 mm. Det er tydelig vist hvordan prisindikatoren for deling bestemmes ved hjelp av et hvilket som helst måleapparat.

Ved å måle en blyant med en lengde som er litt mindre enn 10 cm, vil vi bruke kunnskapen vi har fått. Hvis det ikke var små inndelinger på linjalen, ville konklusjonen følge at objektet har en lengde på 10 cm.Denne omtrentlige verdien kalles målefeilen. Den indikerer nivået av unøyaktighet som kan tolereres i målingen.

Bestemme parametrene for lengden på en blyant med mer høy level nøyaktighet, en større divisjonsverdi oppnår en større målenøyaktighet, noe som gir en mindre feil.

I dette tilfellet kan absolutt nøyaktige målinger ikke gjøres. Og indikatorene bør ikke overstige størrelsen på divisjonsprisen.

Det er fastslått at dimensjonene til målefeilen er ½ av prisen, som er angitt på inndelingene til instrumentet som brukes til å bestemme dimensjonene.

Etter å ha målt blyanten ved 9,7 cm, bestemmer vi indikatorene på feilen. Dette er et gap på 9,65 - 9,85 cm.

Formelen som måler en slik feil er beregningen:

A = a ± D (a)

A - i form av en mengde for måling av prosesser;

a - verdien av måleresultatet;

D - betegnelsen på den absolutte feilen.

Når du trekker fra eller legger til verdier med en feil, vil resultatet bli er lik summen indikatorer på feilen, som er hver enkelt verdi.

Introduksjon til konseptet

Hvis vi vurderer avhengig av måten det uttrykkes på, kan vi skille mellom følgende varianter:

Absolutt.
Slektning.
Gitt.

Den absolutte målefeilen er angitt med stor bokstav "Delta". Dette konseptet er definert som forskjellen mellom de målte og faktiske verdiene for den fysiske mengden som måles.

Uttrykket for den absolutte målefeilen er enhetene for mengden som skal måles.

Ved måling av masse vil den uttrykkes for eksempel i kilo. Dette er ikke en standard for målenøyaktighet.

Hvordan beregne feilen for direkte målinger?

Det finnes måter å representere målefeil og beregne dem på. For å gjøre dette er det viktig å kunne bestemme den fysiske mengden med nødvendig nøyaktighet, å vite hva den absolutte målefeilen er, at ingen noen gang vil kunne finne den. Du kan bare beregne grenseverdien.

Selv om dette begrepet er betinget brukt, indikerer det nøyaktig grensedataene. Absolutte og relative målefeil er angitt med samme bokstaver, forskjellen er i stavemåten.

Ved måling av lengde vil den absolutte feilen måles i de enhetene hvor lengden er beregnet. Og den relative feilen beregnes uten dimensjoner, siden det er forholdet mellom den absolutte feilen og måleresultatet. Denne verdien uttrykkes ofte i prosent eller brøker.

Absolutte og relative målefeil har flere forskjellige måter beregninger avhengig av hvilke fysiske mengder.

Konseptet med direkte måling

Den absolutte og relative feilen for direkte målinger avhenger av enhetens nøyaktighetsklasse og evnen til å bestemme veiefeilen.

Før vi snakker om hvordan feilen beregnes, er det nødvendig å avklare definisjonene. En direkte måling er en måling der resultatet leses direkte fra instrumentvekten.

Når vi bruker termometer, linjal, voltmeter eller amperemeter, utfører vi alltid direkte målinger, siden vi bruker et apparat med en skala direkte.

Det er to faktorer som påvirker ytelsen:

Instrumentfeil.
Feilen i referansesystemet.

Den absolutte feilgrensen for direkte målinger vil være lik summen av feilen som enheten viser og feilen som oppstår under leseprosessen.

D = D (pr.) + D (fraværende)

Eksempel på medisinsk termometer

Nøyaktighetsverdier er angitt på selve instrumentet. En feil på 0,1 grader Celsius registreres på et medisinsk termometer. Lesefeilen er halvparten av divisjonsverdien.

D = C/2

Hvis divisjonsverdien er 0,1 grader, kan det gjøres beregninger for et medisinsk termometer:

D \u003d 0,1 o C + 0,1 o C / 2 \u003d 0,15 o C

På baksiden av skalaen til et annet termometer er det en teknisk spesifikasjon og det er indikert at for de riktige målingene er det nødvendig å senke termometeret med hele bakdelen. ikke spesifisert. Den eneste gjenværende feilen er tellefeilen.

Hvis delingsverdien på skalaen til dette termometeret er 2 o C, så kan du måle temperaturen med en nøyaktighet på 1 o C. Dette er grensene for den tillatte absolutte målefeilen og beregningen av den absolutte målefeilen.

Et spesielt system for beregning av nøyaktighet brukes i elektriske måleinstrumenter.

Nøyaktighet av elektriske måleinstrumenter

For å spesifisere nøyaktigheten til slike enheter, brukes en verdi kalt nøyaktighetsklassen. For betegnelsen brukes bokstaven "Gamma". For nøyaktig å bestemme de absolutte og relative målefeilene, må du vite nøyaktighetsklassen til enheten, som er angitt på skalaen.

Ta for eksempel et amperemeter. Skalaen indikerer nøyaktighetsklassen, som viser tallet 0,5. Den er egnet for målinger på likestrøm og vekselstrøm, refererer til enhetene til det elektromagnetiske systemet.

Dette er en ganske nøyaktig enhet. Hvis du sammenligner det med et skolevoltmeter, kan du se at det har en nøyaktighetsklasse på 4. Denne verdien må være kjent for videre beregninger.

Anvendelse av kunnskap

Dermed D c \u003d c (maks) X γ / 100

Denne formelen vil bli brukt for spesifikke eksempler. La oss bruke et voltmeter og finne feilen i å måle spenningen som batteriet gir.

La oss koble batteriet direkte til voltmeteret, etter å ha sjekket om pilen er på null. Når enheten ble tilkoblet, avviket pilen med 4,2 divisjoner. Denne tilstanden kan beskrives som følger:

Det kan sees at den maksimale verdien av U for denne varen er 6.
Nøyaktighetsklasse -(γ) = 4.
U(o) = 4,2 V.
C=0,2 V

Ved å bruke disse formeldataene beregnes de absolutte og relative målefeilene som følger:

D U \u003d DU (eks.) + C / 2

D U (pr.) \u003d U (maks.) X γ / 100

D U (pr.) \u003d 6 V X 4/100 \u003d 0,24 V

Dette er feilen til enheten.

Beregningen av den absolutte målefeilen i dette tilfellet vil bli utført som følger:

D U = 0,24 V + 0,1 V = 0,34 V

Ved å bruke den betraktede formelen kan du enkelt finne ut hvordan du beregner den absolutte målefeilen.

Det er en regel for avrundingsfeil. Det lar deg finne gjennomsnitt mellom grensen for absolutt feil og relativ feil.

Lære å bestemme veiefeilen

Dette er ett eksempel på direkte målinger. På et spesielt sted er veiing. Spakvekter har tross alt ikke vekt. La oss lære hvordan du bestemmer feilen i en slik prosess. Nøyaktigheten av massemåling påvirkes av nøyaktigheten til vektene og perfeksjonen til selve vekten.

Vi bruker en balansevekt med et sett med vekter som skal plasseres nøyaktig på høyre side av vekten. Ta en linjal for veiing.

Før du starter eksperimentet, må du balansere skalaene. Vi legger linjalen på venstre bolle.

Massen vil være lik summen av de installerte vektene. La oss bestemme målefeilen for denne mengden.

D m = D m (vekter) + D m (vekter)

Massemålefeilen består av to termer knyttet til vekter og vekter. For å finne ut hver av disse verdiene, på fabrikkene for produksjon av vekter og vekter, leveres produktene med spesielle dokumenter som lar deg beregne nøyaktigheten.

Påføring av tabeller

La oss bruke en standardtabell. Feilen på skalaen avhenger av hvor mye masse som legges på skalaen. Jo større den er, jo større er henholdsvis feilen.

Selv om du setter en veldig lett kropp, vil det være en feil. Dette er på grunn av friksjonsprosessen som oppstår i akslene.

Den andre tabellen viser til et sett med vekter. Det indikerer at hver av dem har sin egen massefeil. 10-grammet har en feil på 1 mg, så vel som 20-grammet. Vi beregner summen av feilene til hver av disse vektene, tatt fra tabellen.

Det er praktisk å skrive massen og massefeilen i to linjer, som er plassert under hverandre. Jo mindre vekt, desto mer nøyaktig er målingen.

Resultater

I løpet av det vurderte materialet ble det fastslått at det er umulig å fastslå den absolutte feilen. Du kan bare angi grenseindikatorene. For dette brukes formlene beskrevet ovenfor i beregningene. Dette materialet foreslått til studie på skolen for elever i 8.-9. Basert på den oppnådde kunnskapen er det mulig å løse problemer for å bestemme de absolutte og relative feilene.

I dette emnet vil jeg skrive noe som et kort jukseark om feil. Igjen, denne teksten er på ingen måte offisiell og det er uakseptabelt å referere til den. Jeg vil være takknemlig for korrigering av eventuelle feil og unøyaktigheter som kan være i denne teksten.
Hva er en feil?
Å registrere resultatet av et eksperiment av formen () betyr at hvis vi utfører mange identiske eksperimenter, vil resultatene i 70% ligge i intervallet, og i 30% vil de ikke gjøre det.
Eller, som er det samme, hvis vi gjentar eksperimentet, vil det nye resultatet falle innenfor konfidensintervallet med en sannsynlighet lik konfidenssannsynligheten.
Hvordan runde feilen og resultatet?
Feilen er avrundet til det første signifikante sifferet hvis det ikke er en enhet. Hvis én, så opptil to. Hvori Betydelig figur et hvilket som helst siffer i resultatet unntatt innledende nuller kalles.
Rund til eller eller men på ingen måte eller , siden det er 2 signifikante sifre - 2 og 0 etter toeren.
runde til eller
runde til eller eller
Resultatet er avrundet slik at det siste Betydelig figur Resultatet tilsvarte det siste signifikante tallet for feilen.
Eksempler riktig notasjon:
mm
Mm Vi beholder her i feil 2 signifikante siffer fordi det første signifikante sifferet i feilen er ett.
mm
Eksempler feil oppføring:
Mm. Her ekstra tegn i resultatet. mm ville være riktig.
mm. Her ekstra skilt både ved feil og som et resultat. mm ville være riktig.
I arbeidet mitt bruker jeg verdien gitt meg bare som et tall. For eksempel massen av vekter. Hva er hennes feil?

Hvis feilen ikke er eksplisitt angitt, kan du ta enheten i det siste sifferet. Det vil si at hvis m = 1,35 g skrives, bør 0,01 g tas som en feil.
Det er en funksjon av flere verdier. Hver av disse verdiene har sin egen feil. For å finne feilen til en funksjon, gjør følgende:
Symbolet står for den partielle deriverte av f med hensyn til x. Les mer om partielle derivater.
Anta at du målte samme verdi x flere (n) ganger. Har et sett med verdier. . Du må beregne spredningsfeilen, beregne instrumentell feil og legge dem sammen.
Poengene.
1. Beregn spredningsfeilen
Hvis alle verdiene samsvarer, har du ingen scatter. Ellers er det en spredningsfeil som må beregnes. Til å begynne med beregnes rotmiddelkvadratfeilen til gjennomsnittet:
Her betyr gjennomsnittet over alt.
Spredningsfeilen oppnås ved å multiplisere rms-feilen til gjennomsnittet med elevens koeffisient, som avhenger av konfidensnivået du velger og antall målinger n:
Elevkoeffisienter er hentet fra tabellen under. Konfidensnivået er tilfeldig valgt, antall målinger n vi vet også.
2. Vi tar for oss den instrumentelle feilen til gjennomsnittet
Hvis feilene til forskjellige punkter er forskjellige, i henhold til formelen
I dette tilfellet bør selvfølgelig all tillitssannsynlighet være den samme.
3. Legg sammen gjennomsnittet med en spredning
Feilene legger alltid opp som roten av kvadratene:
I dette tilfellet må du sørge for at tillitssannsynlighetene som de ble beregnet med og sammenfaller.

Hvordan bestemme den instrumentelle feilen til gjennomsnittet fra grafen? Vel, det vil si å bruke parede poengmetoden eller metoden minste kvadrater, finner vi feilen i spredningen av den gjennomsnittlige motstanden. Hvordan finne den instrumentelle feilen til den gjennomsnittlige motstanden?
Både i LSM og i metoden med parede poeng er det mulig å gi et strengt svar på dette spørsmålet. For MNC-forumet i Svetozarov er det ("Fundamentals ...", en seksjon om minste kvadraters metode), og for sammenkoblede punkter er det første du tenker på (på pannen, som de sier) å beregne instrumentell feil for hver skråning. Vel, til alle punkter...
Hvis du ikke vil lide, så er det i Labs en enkel måte å gjøre det på estimater den instrumentelle feilen til vinkelkoeffisienten, nemlig fra LSM følgende (for eksempel før arbeid 1 i laboratoriet "Elektriske måleinstrumenter ..." siste side Metode.anbefalinger).
Hvor er verdien av det maksimale avviket langs Y-aksen til et punkt med en feil fra den tegnede rette linjen, og nevneren er bredden av grafområdet vårt langs Y-aksen. Tilsvarende langs X-aksen.

På motstandsmagasinet står nøyaktighetsklassen: 0,05 / 4 * 10 ^-6? Hvordan finne feilen til enheten fra dette?
Dette betyr at den begrensende relative feilen til enheten (i prosent) har formen:
, hvor
- høyeste verdi lagre motstand, og - den nominelle verdien av den inkluderte motstanden.
Det er lett å se at det andre leddet er viktig når vi jobber med svært lave motstander.
Flere detaljer finner du alltid i enhetspasset. Passet finner du på Internett ved å skrive inn enhetens merke i Google.
Litteratur om feil
Mye mer informasjon om dette emnet finner du i den anbefalte boken for førsteårsstudenter:
V.V. Svetozarov "Elementær behandling av måleresultater"
Som tilleggslitteratur (for førsteårsstudenter tilleggslitteratur) kan vi anbefale:
V.V. Svetozarov "Grunnleggende for statistisk behandling av måleresultater"
Og for de som endelig vil forstå alt, bør du definitivt se her:
J. Taylor. "Introduksjon til teorien om feil"
Takk for at du fant og la ut disse fantastiske bøkene på nettstedet ditt.

Når man måler en hvilken som helst mengde, er det alltid noen avvik fra den sanne verdien, fra det faktum at intet instrument kan gi et nøyaktig resultat. For å bestemme toleranser av de innhentede dataene fra den eksakte verdien, brukes representasjonene av de relative og ubetingede feilene.

Du vil trenge

– resultater av målinger;
- kalkulator.

Instruksjon

1. Først av alt, ta flere målinger med et instrument med samme verdi for å kunne beregne den faktiske verdien. Jo større målingene er, desto mer nøyaktig blir resultatet. Si, vei et eple på en elektronisk vekt. Det er mulig at du fikk totaler på 0,106, 0,111, 0,098 kg.

2. Beregn nå den faktiske verdien av verdien (gyldig, fra det faktum at det er urealistisk å oppdage sannheten). For å gjøre dette legger du sammen resultatene og deler dem med antall målinger, det vil si finn det aritmetiske gjennomsnittet. I eksemplet vil den faktiske verdien være (0,106+0,111+0,098)/3=0,105.

3. For å beregne den ubetingede feilen for den første målingen, trekk den faktiske verdien fra totalen: 0,106-0,105=0,001. Beregn på samme måte de ubetingede feilene til de resterende målingene. Vær oppmerksom på at uansett om resultatet er minus eller pluss, er tegnet på feilen alltid positivt (det vil si at du tar modulen til verdien).

4. For å få den relative feilen til den første målingen, divider den ubetingede feilen med den faktiske verdien: 0,001/0,105=0,0095. Vær oppmerksom på at den relative feilen vanligvis måles som en prosentandel, multipliser derfor det resulterende tallet med 100 %: 0,0095x100 % \u003d 0,95 %. Vurder på samme måte de relative feilene til de gjenværende målingene.

5. Hvis den sanne verdien er bedre kjent, ta umiddelbart i bruk feilberegningen, unntatt søket etter det aritmetiske gjennomsnittet av måleresultatene. Trekk umiddelbart summen fra den sanne verdien, og du vil finne en ubetinget feil.

6. Deretter deler du den ubetingede feilen med den sanne verdien og multipliserer med 100% - dette vil være den relative feilen. La oss si at antallet elever er 197, men det ble rundet opp til 200. I dette tilfellet regner du ut avrundingsfeilen: 197-200=3, relativ feil: 3/197x100%=1,5%.

Feil er en verdi som bestemmer de tillatte avvikene til de mottatte dataene fra den eksakte verdien. Det er representasjoner av relative og ubetingede feil. Å finne dem er en av oppgavene til den matematiske gjennomgangen. I praksis er det imidlertid viktigere å beregne spredningsfeilen til en målt indikator. Fysiske instrumenter har sin egen mulige feil. Men ikke bare det må vurderes når du bestemmer indikatoren. For å beregne spredningsfeilen σ er det nødvendig å utføre flere målinger av denne mengden.

Du vil trenge

Apparat for måling av nødvendig verdi

Instruksjon

1. Mål verdien du trenger med et apparat eller annet måleverktøy. Gjenta målingene flere ganger. Jo større verdier som oppnås, desto høyere nøyaktighet er det å bestemme spredningsfeilen. Tradisjonelt tas det 6-10 målinger. Skriv ned det resulterende settet med verdier for den målte mengden.

2. Hvis alle oppnådde verdier er like, er spredningsfeilen derfor null. Hvis det er forskjellige verdier i serien, beregn spredningsfeilen. For å bestemme det, er det en spesiell formel.

3. I henhold til formelen, beregne først gjennomsnittsverdien<х>fra de mottatte verdiene. For å gjøre dette, legg til alle verdiene, og del summen deres med antall målinger n.

4. Bestem etter tur differansen mellom den totale verdien og gjennomsnittsverdien<х>. Skriv ned summen av de oppnådde forskjellene. Deretter kvadrat alle forskjellene. Finn summen av de gitte kvadratene. Lagre det endelige mottatte beløpet.

5. Regn ut uttrykket n(n-1), der n er antall målinger du tar. Del summen av summen fra forrige beregning med den resulterende verdien.

6. Ta kvadratroten av divisjonen. Dette vil være feilen i spredningen av σ, verdien du målte.

Når du utfører målinger, er det umulig å garantere nøyaktigheten deres, hver enhet gir en viss feil. For å finne ut nøyaktigheten av målinger eller nøyaktighetsklassen til enheten, er det nødvendig å bestemme den ubetingede og relative feil .

Du vil trenge

- flere resultater av målinger eller en annen prøve;
- kalkulator.

Instruksjon

1. Ta målinger minst 3-5 ganger for å kunne beregne den faktiske verdien av parameteren. Legg sammen resultatene og del dem på antall målinger, du får den virkelige verdien, som brukes i oppgaver i stedet for den sannferdige (det er urealistisk å bestemme det). La oss si at hvis målingene ga totalt 8, 9, 8, 7, 10, så vil den faktiske verdien være (8+9+8+7+10)/5=8,4.

2. Oppdag ubetinget feil hele målingen. For å gjøre dette, trekk den faktiske verdien fra måleresultatet, forsøm skiltene. Du vil få 5 ubetingede feil, en for hver måling. I eksemplet vil de være lik 8-8,4 \u003d 0,4, 9-8,4 \u003d 0,6, 8-8,4 \u003d 0,4, 7-8,4 \u003d 1,4, 10-8,4 =1,6 (resultatmoduler er tatt).

3. For å finne ut av slektningen feil av enhver dimensjon, del det ubetingede feil til den faktiske (sanne) verdien. Deretter multipliserer du resultatet med 100%, tradisjonelt måles denne verdien i prosent. I eksemplet oppdager du slektningen feil altså: ?1=0,4/8,4=0,048 (eller 4,8 %), ?2=0,6/8,4=0,071 (eller 7,1 %), ?3=0,4/ 8,4=0,048 (eller 4,8 %), ?4=1,4/8,4 =0,167 (eller 16,7 %), ?5=1,6/8,4=0,19 (eller 19 %).

4. I praksis, for en spesielt nøyaktig visning av feilen, brukes standardavviket. For å finne den, kvadrere alle ubetingede målefeil og legge dem sammen. Deretter deler du dette tallet med (N-1), hvor N er antall målinger. Ved å beregne roten til den resulterende summen, vil du få standardavviket som karakteriserer feil målinger.

5. For å oppdage den ultimate ubetingede feil, finn minimumstallet som er kjent for å være større enn det ubetingede feil eller lik det. I det betraktede eksemplet, velg primitivt den største verdien - 1,6. Det er også av og til nødvendig å finne den begrensende slektningen feil, finn deretter et tall som er større enn eller lik den relative feilen, i eksemplet er det 19 %.

En uatskillelig del av enhver måling er noen feil. Det representerer en god gjennomgang av undersøkelsens nøyaktighet. Etter presentasjonsformen kan den være ubetinget og relativ.

Du vil trenge

- kalkulator.

Instruksjon

1. Feil fysiske målinger delt inn i systematisk, tilfeldig og dristig. De første er forårsaket av faktorer som virker identisk når målinger gjentas mange ganger. De er kontinuerlige eller lovlig endrede. De kan være forårsaket av feil installasjon av enheten eller ufullkommenhet i den valgte målemetoden.

2. Den andre oppstår fra årsakenes kraft og årsaksløs disposisjon. Disse inkluderer feil avrunding ved telling av vitnesbyrd og makt miljø. Hvis slike feil er mye mindre enn delingene av skalaen til dette måleinstrumentet, er det hensiktsmessig å ta en halv divisjon som en ubetinget feil.

3. Savner eller våger feil representerer resultatet av sporing, en som er skarpt forskjellig fra alle de andre.

4. Betingelsesløs feil tilnærmet numerisk verdi er differansen mellom resultatet oppnådd under målingen og den sanne verdien av den målte mengden. En sann eller faktisk verdi gjenspeiler spesielt nøyaktig den fysiske mengden som studeres. Dette feil er det enkleste kvantitative mål på feil. Det kan beregnes ved å bruke følgende formel: ?X = Hisl - Hist. Det kan få positive og negative betydninger. For bedre forståelse, la oss se på et eksempel. Skolen har 1205 elever, når det rundes opp til 1200 ubetinget feil er lik: ? = 1200 - 1205 = 5.

5. Eksistere visse regler beregning av feilen til verdier. For det første ubetinget feil summen av 2 uavhengige verdier er lik summen av deres ubetingede feil: ?(X+Y) = ?X+?Y. En lignende tilnærming gjelder for forskjellen på 2 feil. Det er tillatt å bruke formelen: ?(X-Y) = ?X+?Y.

6. Endringen er en ubetinget feil, tatt med motsatt fortegn: ?p = -?. Den brukes til å eliminere systematiske feil.

målinger fysiske mengder er alltid ledsaget av det ene eller det andre feil. Den representerer avviket til måleresultatene fra den sanne verdien av den målte verdien.

Du vil trenge

-måleverktøy:
-kalkulator.

Instruksjon

1. Feil kan oppstå som et resultat av kraften til ulike faktorer. Blant dem er det tillatt å skille ut ufullkommenheten til midler eller målemetoder, unøyaktigheter i produksjonen, manglende oppfyllelse av spesielle forhold under undersøkelsen.

2. Det er flere klassifiseringer av feil. Ifølge presentasjonsformen kan de være ubetingede, relative og reduserte. De første er forskjellen mellom den beregnede og faktiske verdien av kvantumet. De er uttrykt i enheter av det målte fenomenet og er funnet ved formelen: x = hisl-hist. Sistnevnte bestemmes av forholdet mellom ubetingede feil og verdien av den sanne verdien av indikatoren.Beregningsformelen ser ut som:? = ?х/hist. Det måles i prosenter eller aksjer.

3. Den reduserte feilen til måleanordningen er funnet som et forhold?x til normaliseringsverdien xn. Avhengig av typen enhet, tas den enten lik målegrensen, eller referert til deres spesifikke område.

4. I henhold til opprinnelsesforholdene er det grunnleggende og tilleggs. Hvis målingene ble utført under typiske forhold, vises den første typen. Avvik på grunn av utdata av verdier utenfor de typiske grensene kommer i tillegg. For å evaluere det, etablerer dokumentasjonen vanligvis normer som verdien kan endres innenfor dersom målebetingelsene brytes.

5. Dessuten er feilene ved fysiske målinger delt inn i systematisk, tilfeldig og vågal. Førstnevnte er forårsaket av faktorer som virker ved gjentatte gjentakelser av målinger. Den andre oppstår fra årsakenes kraft og årsaksløs disposisjon. En glipp er resultatet av sporing, en som er drastisk forskjellig fra alle de andre.

6. Avhengig av arten av den målte mengden, ulike metoder feilmåling. Den første av disse er Kornfeld-metoden. Den er basert på beregningen av et konfidensintervall som strekker seg fra den minste til den største totalen. Feilen i dette tilfellet vil være halvparten av differansen mellom disse summene: ?x = (xmax-xmin)/2. En annen metode er beregning av rotmiddelkvadratfeilen.

Målinger kan utføres med ulik grad av nøyaktighet. Samtidig er selv presisjonsinstrumenter absolutt ikke nøyaktige. Ubetingede og relative feil kan være små, men i realiteten er de så å si uendret. Forskjellen mellom omtrentlig og eksakte verdier en viss verdi kalles ubetinget feil. I dette tilfellet kan avviket være både stort og lite.

Du vil trenge

– måledata;
- kalkulator.

Instruksjon

1. Før du beregner den ubetingede feilen, ta flere postulater som innledende data. Eliminer dristige feil. Godta at nødvendige korreksjoner allerede er beregnet og lagt til totalen. En slik korreksjon kan for eksempel være overføring av utgangspunktet for målinger.

2. Ta det som er kjent som startsted, og tilfeldige feil tas i betraktning. Dette innebærer at de er mindre systematiske, det vil si ubetingede og relative, karakteristiske for denne spesielle enheten.

3. Tilfeldige feil påvirker resultatet av selv høypresisjonsmålinger. Følgelig vil hvert resultat være mer eller mindre nær det ubetingede, men det vil alltid være avvik. Definer dette intervallet. Det kan uttrykkes med formelen (Xism-?X)?Chism? (Hizm+?X).

4. Bestem verdien nærmest den sanne verdien. Ved reelle målinger tas det aritmetiske gjennomsnittet, som kan finnes ved hjelp av formelen vist i figuren. Ta totalen som den sanne verdien. I mange tilfeller blir avlesningen av et referanseinstrument tatt som nøyaktig.

5. Når du kjenner den sanne verdien av målingen, kan du finne den absolutte feilen, som må vurderes i alle etterfølgende målinger. Oppdag x1 verdi - data en viss dimensjon. Bestem forskjellen X, trekke fra mer mindre. Ved bestemmelse av feilen tas det kun hensyn til modulen til denne forskjellen.

Merk!
Som vanlig er det i praksis umulig å utføre en ubetinget nøyaktig måling. Følgelig tas den marginale feilen som referanseverdi. Hun representerer høyeste verdi modul for ubetinget feil.

Nyttige råd
I utilitaristiske målinger blir verdien av den ubetingede feilen vanligvis antatt å være halvparten laveste pris inndeling. Når man arbeider med tall, tas den ubetingede feilen til å være halvparten av verdien av sifferet, som er i neste kategori etter de eksakte sifrene. For å bestemme nøyaktighetsklassen til enheten, er det viktigste forholdet mellom den ubetingede feilen og resultatet av målinger eller til lengden på skalaen.

Målefeil er assosiert med ufullkommenhet av instrumenter, verktøy, metodikk. Nøyaktigheten avhenger også av observasjon og eksperimentatorens tilstand. Feil deles inn i ubetinget, relativ og redusert.

Instruksjon

1. La en enkelt måling av verdien gi totalt x. Den sanne verdien er angitt med x0. Så det ubetingede feil?x=|x-x0|. Den estimerer den ubetingede målefeilen. Betingelsesløs feil består av 3 komponenter: tilfeldige feil, systematiske feil og glipp. Vanligvis, når man måler med et instrument, tas halve divisjonsverdien som en feil. For en millimeterlinjal vil dette være 0,5 mm.

2. Den sanne verdien av den målte verdien er i intervallet (x-?x; x+?x). Kort fortalt skrives dette som x0=x±?x. Det viktigste er å måle x og ?x i samme måleenheter og skrive tallene i samme format, for eksempel en heltallsdel og tre sifre etter desimaltegnet. Det viser seg, ubetinget feil gir grensene for intervallet der den sanne verdien ligger med en viss sannsynlighet.

3. Slektning feil uttrykker forholdet mellom ubetinget feil og den faktiske verdien av mengden: ?(x)=?x/x0. Dette er en dimensjonsløs mengde, den kan også skrives i prosent.

4. Målingene er enten direkte eller indirekte. Ved direkte målinger måles den ønskede verdien umiddelbart med et egnet instrument. La oss si at lengden på kroppen måles med en linjal, spenningen måles med et voltmeter. Ved indirekte målinger finner man verdien i henhold til formelen for forholdet mellom den og de målte verdiene.

5. Hvis resultatet er en forbindelse fra 3 lett målte størrelser med feil ?x1, ?x2, ?x3, så feil indirekte måling?F=?[(?x1 ?F/?x1)?+(?x2 ?F/?x2)?+(?x3 ?F/?x3)?]. Her?F/?x(i) er de partielle deriverte av funksjonen med hensyn til noen av de fritt målbare størrelsene.

Nyttige råd
Glipp er frekke målingsunøyaktigheter som oppstår når instrumentene ikke fungerer, forsøkslederens uoppmerksomhet og brudd på den eksperimentelle metodikken. For å redusere sannsynligheten for slike feil, vær forsiktig når du tar målinger og beskriv resultatet i detalj.

Resultatet av enhver måling er uunngåelig ledsaget av et avvik fra den sanne verdien. Det er mulig å beregne målefeilen ved hjelp av flere metoder, avhengig av typen, for eksempel statistiske metoder for å bestemme konfidensintervall, standardavvik, etc.

Instruksjon

1. Det er flere grunner til at det er det feil målinger. Dette er instrumentelle unøyaktigheter, ufullkommenhet i metodikken, samt feil forårsaket av uoppmerksomhet fra operatøren som tar målinger. I tillegg blir ofte den sanne verdien av en parameter tatt for å være dens faktiske verdi, noe som faktisk bare er spesielt mulig, basert på en gjennomgang av et statistisk utvalg av resultatene fra en serie eksperimenter.

2. En feil er et mål på avviket til en målt parameter fra dens sanne verdi. I henhold til Kornfeld-metoden bestemmes et konfidensintervall, et som garanterer en viss grad av sikkerhet. Samtidig finner man de såkalte konfidensgrensene, der verdien svinger, og feilen beregnes som en halv sum av disse verdiene:? = (xmax – xmin)/2.

3. Dette er et intervallanslag. feil, som er fornuftig å utføre med en liten mengde statistisk prøvetaking. Punktestimering består i å beregne den matematiske forventningen og standardavviket.

4. Forventet verdi er den integrerte summen av en serie produkter med 2 sporingsparametere. Dette er faktisk verdiene til den målte mengden og dens sannsynligheter på disse punktene: М = ?xi pi.

5. Den klassiske formelen for beregning av standardavviket antar beregningen av gjennomsnittsverdien av den analyserte sekvensen av verdier av den målte verdien, og vurderer også volumet til en serie utførte eksperimenter: = ?(?(xi – xav)?/(n – 1)).

6. Etter uttrykksmetoden skilles også ubetingede, relative og reduserte feil. Den ubetingede feilen uttrykkes i de samme enhetene som den målte verdien, og er lik differansen mellom dens beregnede og sanne verdi: x = x1 - x0.

7. Den relative målefeilen er relatert til den ubetingede, men den er mer effektiv. Den har ingen dimensjon, noen ganger er den uttrykt som en prosentandel. Dens verdi er lik forholdet mellom det ubetingede feil til den sanne eller beregnede verdien av den målte parameteren:?x = ?x/x0 eller?x = ?x/x1.

8. Den reduserte feilen uttrykkes som forholdet mellom den ubetingede feilen og en konvensjonelt akseptert verdi x, som er konstant for alle målinger og bestemmes av graderingen av instrumentskalaen. Hvis skalaen starter fra null (ensidig), er denne normaliseringsverdien lik dens øvre grense, og hvis den er tosidig, bredden på hvert av dens områder:? = ?x/xn.

Selvledelse ved diabetes anses som en viktig del av behandlingen. Et glukometer brukes til å måle blodsukkeret hjemme. Den mulige feilen for denne enheten er høyere enn for glykemiske laboratorieanalysatorer.

Måling av blodsukker er nødvendig for å evaluere effektiviteten av diabetesbehandling og for å justere dosen av legemidler. Det avhenger av den foreskrevne behandlingen hvor mange ganger i måneden du trenger å måle sukker. Noen ganger er det nødvendig med blodprøvetaking for gjennomgang gjentatte ganger i løpet av dagen, noen ganger ganske 1-2 ganger i uken. Selvkontroll er utelukkende nødvendig for gravide kvinner og pasienter med type 1 diabetes.

Tillatt feil for et glukometer i henhold til internasjonale standarder

Glukometeret regnes ikke som et presisjonsinstrument. Det er kun tilberedt for en omtrentlig bestemmelse av konsentrasjonen av sukker i blodet. Den mulige feilen til et glukometer i henhold til verdensstandarder er 20% med en glykemi på mer enn 4,2 mmol / l. For eksempel, hvis et sukkernivå på 5 mmol/l er fastsatt under selvkontroll, er den reelle verdien av konsentrasjonen i området fra 4 til 6 mmol/l. Den mulige feilen til et glukometer under standardforhold måles i prosent, og ikke i mmol / l. Jo høyere indikatorene er, desto større er feilen i ubetingede tall. Si at hvis blodsukkeret når ca. 10 mmol/l, så overstiger ikke feilen 2 mmol/l, og hvis sukkeret er ca. 20 mmol/l, så er forskjellen med totalen laboratoriemåling kan være opptil 4 mmol/l. I de fleste tilfeller overvurderer glukometeret glykemi.Standarder tillater at den oppgitte målefeilen overskrides i 5 % av tilfellene. Dette betyr at enhver tjuende undersøkelse kan forvrenge resultatene betydelig.

Tillatt feil for glukometer fra forskjellige selskaper

Glukometre er underlagt obligatorisk sertifisering. Dokumentene som følger med enheten viser vanligvis tallene for mulig målefeil. Hvis dette elementet ikke er i instruksjonene, tilsvarer feilen 20 %. Noen målerprodusenter legger spesiell vekt på målenøyaktighet. Det er enheter fra europeiske selskaper som har en mulig feil på mindre enn 20 %. Den beste indikatoren i dag er 10-15%.

Feilen til glukometeret under egenkontroll

Den tillatte målefeilen karakteriserer driften av enheten. Flere andre faktorer påvirker også nøyaktigheten av undersøkelsen. Unormalt forberedt hud, for liten eller for stor dråpe blod mottatt, uakseptabelt temperaturregime- alt dette kan føre til feil. Bare hvis alle reglene for selvkontroll blir overholdt, er det tillatt å stole på den erklærte mulige feilen i undersøkelsen. Reglene for egenkontroll med støtte fra et glukosemåler kan fås hos behandlende lege. Nøyaktigheten til glukosemåleren kan sjekkes i service Senter. Produsentens garantier inkluderer gratis konsultasjoner og feilsøking.