Kriterium für die lineare Abhängigkeit von Vektoren in rn. Drei Arten linearer Abhängigkeit

Voraussetzung lineare Abhängigkeit von n Funktionen.

Lassen Sie die Funktionen Ableitungen des Grenzwerts (n-1) haben.

Betrachten Sie die Determinante: (1)

W(x) wird üblicherweise als Wronski-Determinante für Funktionen bezeichnet.

Satz 1. Sind die Funktionen im Intervall (a,b) linear abhängig, so ist ihr Wronskian W(x) in diesem Intervall identisch gleich Null.

Nachweisen. Gemäß den Bedingungen des Satzes ist die Beziehung erfüllt

, (2) wobei nicht alle gleich Null sind. Lassen . Dann

(3). Wir differenzieren diese Identität n-1 Mal und

Einsetzen ihrer resultierenden Werte in die Wronsky-Determinante,

wir bekommen:

In der Wronski-Determinante ist die letzte Spalte eine Linearkombination der vorherigen n-1 Spalten und daher an allen Punkten des Intervalls (a,b) gleich Null.

Satz 2. Wenn die Funktionen y 1 ,..., y n linear unabhängige Lösungen der Gleichung L[y] = 0 sind, deren Koeffizienten alle im Intervall (a,b) stetig sind, dann ist der Wronski-Operator dieser Lösungen jeweils ungleich Null Punktintervall (a,b).

Nachweisen. Nehmen wir das Gegenteil an. Es gibt X 0, wobei W(X 0)=0. Erstellen wir ein System aus n Gleichungen

Offensichtlich hat System (5) eine Lösung ungleich Null. Sei (6).

Machen wir eine lineare Kombination der Lösungen y 1,..., y n.

Y(x) ist eine Lösung der Gleichung L[y] = 0. Darüber hinaus ist . Aufgrund des Eindeutigkeitssatzes darf die Lösung der Gleichung L[y] = 0 mit Null-Anfangsbedingungen nur Null sein, ᴛ.ᴇ. .

Wir erhalten die Identität, wenn nicht alle gleich Null sind, was bedeutet, dass y 1 ,..., y n linear abhängig sind, was den Bedingungen des Satzes widerspricht. Folglich gibt es keinen solchen Punkt, an dem W(X 0)=0 ist.

Basierend auf Satz 1 und Satz 2 kann die folgende Aussage formuliert werden. Damit n Lösungen der Gleichung L[y] = 0 im Intervall (a,b) linear unabhängig sind, ist es äußerst wichtig und ausreichend, dass ihr Wronski-Operator an keinem Punkt in diesem Intervall verschwindet.

Aus den bewährten Theoremen ergeben sich auch die folgenden offensichtlichen Eigenschaften des Wronski-Operators.

1. Wenn der Wronskian von n Lösungen der Gleichung L[y] = 0 an einem Punkt x = x 0 aus dem Intervall (a,b), in dem alle Koeffizienten p i (x) stetig sind, gleich Null ist, dann ist er gleich zu jedem Zeitpunkt ab Punkten dieses Intervalls auf Null.
2. Wenn der Wronski-Operator von n Lösungen der Gleichung L[y] = 0 an einem Punkt x = x0 aus dem Intervall (a,b) ungleich Null ist, dann ist er an allen Punkten dieses Intervalls ungleich Null.

Für die Linearität von n unabhängigen Lösungen der Gleichung L[y] = 0 im Intervall (a,b), in dem die Koeffizienten der Gleichung p i (x) stetig sind, ist es jedoch äußerst wichtig und ausreichend, dass ihr Wronskian an mindestens einem Punkt dieses Intervalls von Null verschieden sein.

Eine notwendige Bedingung für die lineare Abhängigkeit von n Funktionen. - Konzept und Typen. Klassifizierung und Merkmale der Kategorie „Notwendige Bedingung für die lineare Abhängigkeit von n Funktionen.“ 2017, 2018.

Bordausrüstung für den Ladungsumschlag Vortrag Nr. 6 Thema: Ladungsausrüstung 6.1. Bordausrüstung für den Frachtumschlag. 6.2. Frachtkräne. 6.3. Rampe. Überladung ist die Bewegung von Ladung auf oder von

2. Du weißt nicht, wo Sasha ist? 3. Wissen Sie nicht, wo sich die Bibliothek befindet?4. Du weißt nicht, wo Olya jetzt ist?, ..., 5. Du weißt nicht, wo Natasha jetzt ist?Guten Tag Mich... .- Bestimmung von Zmin und Xmin aus der Bedingung, dass keine Hinterschneidung vorliegtAbb.5.9. Über das Trimmen der Radzähne. Betrachten wir, wie der Scherkoeffizient x der Zahnstange mit der Anzahl der Zähne zusammenhängt, die von der Zahnstange am Rad geschnitten werden können. Lassen Sie die Schiene in Position 1 montieren (Abb. 5.9.). In diesem Fall schneidet die gerade Linie der Zahnstangenköpfe die N-N-Eingriffslinie in ... Definition 18.2 Funktionssystem F 5 f p

angerufen l i- neip o H

und in und mit und m. ungefähr th auf dem Intervall(A,

(3), wenn einige nicht trivial

Eine lineare Kombination dieser Funktionen ist in diesem Intervall identisch Null: Definition 18.3 Betrachten wir, wie der Scherkoeffizient x der Zahnstange mit der Anzahl der Zähne zusammenhängt, die von der Zahnstange am Rad geschnitten werden können. Lassen Sie die Schiene in Position 1 montieren (Abb. 5.9.). In diesem Fall schneidet die gerade Linie der Zahnstangenköpfe die N-N-Eingriffslinie in ... Vektorsystem Funktionssystem f 1, ...,

Es ist wichtig, den Zusammenhang dieser drei Konzepte (lineare Abhängigkeit von Funktionen, Vektoren und Vektorfunktionen) untereinander zu verstehen.

Wenn wir zunächst Formel (18.6) in erweiterter Form präsentieren (wobei wir uns daran erinnern, dass jede davon x g (1) ist ein Vektor)

dann erweist es sich als äquivalent zum System der Gleichheiten

bedeutet linear G-X-Sucht Komponenten im Sinne der ersten Definition (als Funktionen). Sie sagen, dass die lineare Abhängigkeit von Vektorfunktionen sie mit sich bringt Komponente für Komponente lineare Abhängigkeit.

Das Umgekehrte gilt im Allgemeinen nicht: Es reicht aus, das Beispiel eines Vektorfunktionspaars zu betrachten

Die ersten Komponenten dieser Vektorfunktionen fallen einfach zusammen, sind also linear abhängig. Die zweiten Komponenten sind also proportional. sind ebenfalls linear abhängig. Versuchen wir jedoch, ihre Linearkombination, die identisch gleich Null ist, aus der Beziehung zu konstruieren

Wir bekommen das System sofort

das eine einzigartige Lösung hat S - S-2 - 0. Somit sind unsere Vektorfunktionen linear unabhängig.

Was ist der Grund für diese seltsame Eigenschaft? Was ist der Trick, mit dem man aus offensichtlich abhängigen Funktionen linear unabhängige Vektorfunktionen konstruieren kann?

Es stellt sich heraus, dass der springende Punkt nicht so sehr in der linearen Abhängigkeit der Komponenten liegt, sondern im Verhältnis der Koeffizienten, das erforderlich ist, um Null zu erhalten. Im Falle einer linearen Abhängigkeit von Vektorfunktionen bedient derselbe Satz von Koeffizienten alle Komponenten unabhängig von ihrer Anzahl. Aber in dem Beispiel, das wir gegeben haben, erforderte eine Komponente einen Koeffizientenanteil und eine andere einen anderen. Der Trick ist also eigentlich einfach: Um aus einer „komponentenweisen“ linearen Abhängigkeit die gesamte lineare Abhängigkeit von Vektorfunktionen zu erhalten, ist es notwendig, dass alle Komponenten „im gleichen Verhältnis“ linear abhängig sind.

Kommen wir nun zur Untersuchung des Zusammenhangs zwischen der linearen Abhängigkeit von Vektorfunktionen und Vektoren. Hier ist die Tatsache fast offensichtlich, dass aus der linearen Abhängigkeit der Vektorfunktionen für jede feste Funktion folgt T* Vektor

wird linear abhängig sein.

Das Umgekehrte gilt im Allgemeinen nicht: aus der linearen Abhängigkeit der Vektoren für jeden T Die lineare Abhängigkeit von Vektorfunktionen folgt nicht. Am Beispiel zweier Vektorfunktionen lässt sich dies leicht erkennen

Bei t=1, t=2 und t=3 wir erhalten Paare von Vektoren

jeweils. Jedes Vektorpaar ist proportional (mit den Koeffizienten 1,2 bzw. 3). Das ist bei jedem Festnetz leicht zu verstehen T* Unser Vektorpaar ist proportional zum Koeffizienten T*.

Wenn wir versuchen, eine Linearkombination von Vektorfunktionen zu konstruieren, die identisch gleich Null ist, dann geben uns bereits die ersten Komponenten den Zusammenhang

was nur möglich ist, wenn MIT = MIT2 = 0. Somit erwiesen sich unsere Vektorfunktionen als linear unabhängig. Auch hier liegt die Erklärung für diesen Effekt darin, dass im Fall einer linearen Abhängigkeit von Vektorfunktionen derselbe Satz von Konstanten Cj alle Werte bedient T, und in unserem Beispiel für jeden Wert T ein bestimmtes Verhältnis zwischen den Koeffizienten war erforderlich.

Von uns vorgestellt lineare Operationen auf Vektoren ermöglichen die Erstellung verschiedener Ausdrücke für Vektorgrößen und transformieren Sie sie mithilfe der für diese Operationen festgelegten Eigenschaften.

Basierend auf einem gegebenen Satz von Vektoren a 1, ..., a n können Sie einen Ausdruck der Form erstellen

wobei a 1, ... und n beliebig sind reelle Zahlen. Dieser Ausdruck heißt lineare Kombination von Vektoren a 1, ..., a n. Die Zahlen α i, i = 1, n, repräsentieren Linearkombinationskoeffizienten. Man nennt auch eine Menge von Vektoren System von Vektoren.

Im Zusammenhang mit dem eingeführten Konzept einer Linearkombination von Vektoren stellt sich das Problem, eine Menge von Vektoren zu beschreiben, die als Linearkombination eines gegebenen Vektorsystems a 1, ..., a n geschrieben werden kann. Darüber hinaus stellen sich natürlich Fragen nach den Bedingungen, unter denen es eine Darstellung eines Vektors in Form einer Linearkombination gibt, und nach der Einzigartigkeit einer solchen Darstellung.

Definition 2.1. Es werden die Vektoren a 1, ... und n aufgerufen linear abhängig, wenn es einen Satz von Koeffizienten α 1 , ... , α n gibt, so dass

α 1 a 1 + ... + α n à n = 0 (2.2)

und mindestens einer dieser Koeffizienten ist ungleich Null. Wenn der angegebene Koeffizientensatz nicht existiert, werden die Vektoren aufgerufen linear unabhängig.

Wenn α 1 = ... = α n = 0, dann gilt offensichtlich α 1 a 1 + ... + α n a n = 0. Vor diesem Hintergrund können wir Folgendes sagen: Vektoren a 1, ... und n sind linear unabhängig, wenn aus Gleichung (2.2) folgt, dass alle Koeffizienten α 1 , ... , α n gleich Null sind.

Der folgende Satz erklärt, warum das neue Konzept den Begriff „Abhängigkeit“ (oder „Unabhängigkeit“) trägt, und liefert ein einfaches Kriterium für lineare Abhängigkeit.

Satz 2.1. Damit die Vektoren a 1, ... und n, n > 1 linear abhängig sind, ist es notwendig und ausreichend, dass einer von ihnen eine Linearkombination der anderen ist.

◄ Notwendigkeit. Nehmen wir an, dass die Vektoren a 1, ... und n linear abhängig sind. Gemäß Definition 2.1 der linearen Abhängigkeit gibt es in Gleichheit (2.2) auf der linken Seite mindestens einen Koeffizienten ungleich Null, zum Beispiel α 1. Wir lassen den ersten Term auf der linken Seite der Gleichheit und verschieben den Rest auf die rechte Seite, wobei wir wie üblich ihre Vorzeichen ändern. Wenn wir die resultierende Gleichheit durch α 1 dividieren, erhalten wir

a 1 =-α 2 /α 1 ⋅ a 2 - ... - α n /α 1 ⋅ a n

diese. Darstellung des Vektors a 1 als Linearkombination der übrigen Vektoren a 2, ..., a n.

Angemessenheit. Lassen Sie zum Beispiel den ersten Vektor a 1 als lineare Kombination der übrigen Vektoren darstellen: a 1 = β 2 a 2 + ... + β n a n. Wenn wir alle Terme von der rechten Seite nach links übertragen, erhalten wir a 1 - β 2 a 2 - ... - β n a n = 0, d.h. eine lineare Kombination von Vektoren a 1, ..., a n mit Koeffizienten α 1 = 1, α 2 = - β 2, ..., α n = - β n, gleich Nullvektor. In dieser Linearkombination sind nicht alle Koeffizienten Null. Nach Definition 2.1 sind die Vektoren a 1, ... und n linear abhängig.

Die Definition und das Kriterium der linearen Abhängigkeit werden so formuliert, dass sie das Vorhandensein von zwei oder mehr Vektoren implizieren. Wir können jedoch auch von einer linearen Abhängigkeit eines Vektors sprechen. Um diese Möglichkeit zu realisieren, müssen Sie statt „Vektoren sind linear abhängig“ sagen: „Das Vektorsystem ist linear abhängig.“ Es ist leicht zu erkennen, dass der Ausdruck „ein System aus einem Vektor ist linear abhängig“ bedeutet, dass dieser einzelne Vektor Null ist (in einer Linearkombination gibt es nur einen Koeffizienten und dieser sollte nicht gleich Null sein).

Das Konzept der linearen Abhängigkeit hat eine einfache geometrische Interpretation. Die folgenden drei Aussagen verdeutlichen diese Interpretation.

Satz 2.2. Zwei Vektoren sind genau dann linear abhängig, wenn sie kollinear.

◄ Wenn die Vektoren a und b linear abhängig sind, dann wird einer von ihnen, zum Beispiel a, durch den anderen ausgedrückt, d.h. a = λb für eine reelle Zahl λ. Gemäß Definition 1.7 funktioniert Vektoren pro Zahl, die Vektoren a und b sind kollinear.

Seien nun die Vektoren a und b kollinear. Wenn beide Null sind, ist es offensichtlich, dass sie linear abhängig sind, da jede lineare Kombination von ihnen gleich dem Nullvektor ist. Einer dieser Vektoren sei ungleich 0, zum Beispiel Vektor b. Bezeichnen wir mit λ das Verhältnis der Vektorlängen: λ = |a|/|b|. Kollineare Vektoren können sein unidirektional oder entgegengesetzt gerichtet. Im letzteren Fall ändern wir das Vorzeichen von λ. Wenn wir dann Definition 1.7 überprüfen, sind wir überzeugt, dass a = λb. Nach Satz 2.1 sind die Vektoren a und b linear abhängig.

Bemerkung 2.1. Im Fall zweier Vektoren lässt sich der bewährte Satz unter Berücksichtigung des Kriteriums der linearen Abhängigkeit wie folgt umformulieren: Zwei Vektoren sind genau dann kollinear, wenn einer von ihnen als Produkt des anderen durch eine Zahl dargestellt wird. Dies ist ein praktisches Kriterium für die Kollinearität zweier Vektoren.

Satz 2.3. Drei Vektoren sind genau dann linear abhängig, wenn sie koplanar.

◄ Wenn drei Vektoren a, b, c linear abhängig sind, dann ist nach Satz 2.1 einer von ihnen, zum Beispiel a, eine Linearkombination der anderen: a = βb + γc. Kombinieren wir die Ursprünge der Vektoren b und c am Punkt A. Dann haben die Vektoren βb, γс einen gemeinsamen Ursprung am Punkt A und entlang Nach der Parallelogrammregel beträgt ihre Summe diese. Vektor a wird ein Vektor mit Ursprung A und sein das Ende, der der Scheitelpunkt eines Parallelogramms ist, das aus Komponentenvektoren aufgebaut ist. Somit liegen alle Vektoren in derselben Ebene, also koplanar.

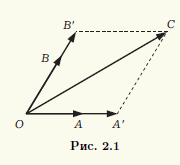
Die Vektoren a, b, c seien koplanar. Wenn einer dieser Vektoren Null ist, ist es offensichtlich, dass es sich um eine Linearkombination der anderen handelt. Es reicht aus, alle Koeffizienten der Linearkombination zu nehmen gleich Null. Daher können wir davon ausgehen, dass alle drei Vektoren nicht Null sind. Kompatibel begonnen diese Vektoren in gemeinsamer Punkt O. Ihre Enden seien die Punkte A, B bzw. C (Abb. 2.1). Durch Punkt C zeichnen wir Linien parallel zu Linien, die durch Punktepaare O, A und O, B verlaufen. Wenn wir die Schnittpunkte als A" und B" bezeichnen, erhalten wir ein Parallelogramm OA"CB", also OC" = OA" + OB". Der Vektor OA" und der Nicht-Null-Vektor a = OA sind kollinear, und daher kann der erste von ihnen durch Multiplikation des zweiten mit einer reellen Zahl α:OA" = αOA erhalten werden. Ebenso gilt OB" = βOB, β ∈ R. Als Ergebnis erhalten wir OC" = α OA. + βOB, d. h. Vektor c ist eine Linearkombination der Vektoren a und b. Nach Satz 2.1 sind die Vektoren a, b, c linear abhängig.

Satz 2.4. Alle vier Vektoren sind linear abhängig.

◄ Wir führen den Beweis nach dem gleichen Schema wie in Satz 2.3 durch. Betrachten Sie beliebige vier Vektoren a, b, c und d. Wenn einer der vier Vektoren Null ist oder es zwei kollineare Vektoren unter ihnen gibt oder drei der vier Vektoren koplanar sind, dann sind diese vier Vektoren linear abhängig. Wenn beispielsweise die Vektoren a und b kollinear sind, können wir ihre Linearkombination αa + βb = 0 mit Koeffizienten ungleich Null erstellen und dann die verbleibenden zwei Vektoren zu dieser Kombination hinzufügen, wobei wir Nullen als Koeffizienten verwenden. Wir erhalten eine lineare Kombination von vier Vektoren gleich 0, in denen es Koeffizienten ungleich Null gibt.

Daher können wir davon ausgehen, dass unter den ausgewählten vier Vektoren kein Vektor Null ist, keine zwei kollinear sind und keine drei koplanar sind. Wählen wir Punkt O als gemeinsamen Anfang. Dann sind die Enden der Vektoren a, b, c, d einige Punkte A, B, C, D (Abb. 2.2). Durch Punkt D zeichnen wir drei Ebenen parallel zu den Ebenen OBC, OCA, OAB und seien A“, B“, C“ die Schnittpunkte dieser Ebenen mit den Geraden OA, OB, OS. Wir erhalten a Parallelepiped OA" C "B" C" B"DA", und die Vektoren a, b, c liegen auf seinen Kanten, die vom Scheitelpunkt O ausgehen. Da das Viereck OC"DC" ein Parallelogramm ist, gilt OD = OC" + OC „Das Segment OC“ wiederum ist ein Parallelogramm OA“C“B“, also OC“ = OA“ + OB“ und OD = OA“ + OB“ + OC“.

Es bleibt zu beachten, dass die Vektorpaare OA ≠ 0 und OA" , OB ≠ 0 und OB" , OC ≠ 0 und OC" kollinear sind und es daher möglich ist, die Koeffizienten α, β, γ so auszuwählen OA" = αOA , OB" = βOB und OC" = γOC. Wir erhalten schließlich OD = αOA + βOB + γOC. Folglich wird der OD-Vektor durch die anderen drei Vektoren ausgedrückt, und alle vier Vektoren sind gemäß Satz 2.1 linear abhängig.

Eine notwendige und hinreichende Bedingung für die lineare Abhängigkeit von zwei

Vektoren ist ihre Kollinearität.

2. Punktprodukt- eine Operation an zwei Vektoren, deren Ergebnis ein Skalar (Zahl) ist, der nicht vom Koordinatensystem abhängt und die Längen der Faktorvektoren und den Winkel zwischen ihnen charakterisiert. Diese Operation entspricht einer Multiplikation Länge gegebener Vektor x auf Vorsprung einen anderen Vektor y zu einem gegebenen Vektor x. Diese Operation wird normalerweise in jedem Faktor als kommutativ und linear betrachtet.

Eigenschaften des Skalarprodukts:

3. Drei Vektoren (oder größere Zahl) heißen koplanar, wenn sie, auf einen gemeinsamen Ursprung reduziert, in derselben Ebene liegen.

Eine notwendige und hinreichende Bedingung für die lineare Abhängigkeit von drei Vektoren ist ihre Koplanarität. Alle vier Vektoren sind linear abhängig. Basis im Weltraum ist ein beliebiges geordnetes Tripel nichtkoplanarer Vektoren. Eine Basis im Raum ermöglicht die eindeutige Zuordnung jedes Vektors zu einem geordneten Zahlentripel – den Koeffizienten der Darstellung dieses Vektors in einer Linearkombination von Basisvektoren. Im Gegensatz dazu verknüpfen wir mit einer Basis einen Vektor mit jedem geordneten Zahlentripel, wenn wir eine lineare Kombination erstellen, die als orthogonale Basis bezeichnet wird orthonormal , wenn seine Vektoren gleich eins sind. Für eine Orthonormalbasis im Raum wird häufig die Notation verwendet. Satz: Bei einer Orthonormalbasis sind die Koordinaten der Vektoren die entsprechenden orthogonalen Projektionen dieses Vektors auf die Richtungen der Koordinatenvektoren. Tripel nichtkoplanarer Vektoren a, b, c angerufen Rechts, wenn der Beobachter von ihrem gemeinsamen Ursprung aus die Enden der Vektoren umgeht a, b, c in der angegebenen Reihenfolge scheint im Uhrzeigersinn zu erfolgen. Ansonsten a, b, c - noch drei übrig. Alle rechten (oder linken) Vektortripel werden aufgerufen gleichermaßen orientiert. Ein rechtwinkliges Koordinatensystem auf einer Ebene wird durch zwei zueinander senkrechte Koordinatenachsen gebildet OCHSE Und OY. Die Koordinatenachsen schneiden sich im Punkt O, der Ursprung genannt wird, wird auf jeder Achse die positive Richtung gewählt. IN rechtsseitig Koordinatensystem, die positive Richtung der Achsen wird so gewählt, dass wenn die Achse gerichtet ist OY hoch, Achse OCHSE schaute nach rechts.

Vier Ecken (I, II, III, IV), die durch die Koordinatenachsen gebildet werden X"X Und Y"Y, heißen Koordinatenwinkel oder Quadranten(siehe Abb. 1).

wenn die Vektoren und relativ zu einer orthonormalen Basis auf der Ebene Koordinaten bzw. haben, dann wird das Skalarprodukt dieser Vektoren durch die Formel berechnet

4. Kreuzprodukt zweier Vektoren a und b ist eine Operation auf ihnen, die nur in definiert ist dreidimensionaler Raum, dessen Ergebnis ist Vektor mit folgendem

Eigenschaften:

Die geometrische Bedeutung des Kreuzprodukts von Vektoren ist die Fläche eines aus den Vektoren aufgebauten Parallelogramms. Eine notwendige und hinreichende Bedingung für die Kollinearität eines Vektors ungleich Null und eines Vektors ist die Existenz einer Zahl, die die Gleichheit erfüllt.

Wenn zwei Vektoren und durch ihr Rechteck definiert sind Kartesische Koordinaten, oder genauer gesagt, werden auf einer vortonormierten Basis dargestellt

und das Koordinatensystem stimmt, dann sind es ihre Vektorprodukt sieht aus wie

Um sich diese Formel zu merken, ist es praktisch, die Determinante zu verwenden:

5. Gemischtes Produkt Vektoren – das Skalarprodukt eines Vektors und das Vektorprodukt von Vektoren und:

Manchmal heißt es dreifaches Skalarprodukt Vektoren, höchstwahrscheinlich aufgrund der Tatsache, dass das Ergebnis ein Skalar (genauer gesagt ein Pseudoskalar) ist.

Geometrische Bedeutung: Der Modul des gemischten Produkts ist numerisch gleich dem Volumen des durch die Vektoren gebildeten Parallelepipeds.

Wenn zwei Faktoren umgeordnet werden, ändert das gemischte Produkt das Vorzeichen in das Gegenteil:

Bei einer zyklischen (zirkulären) Umlagerung von Faktoren ändert sich das Mischprodukt nicht:

Das Mischprodukt ist in jedem Faktor linear.

Das gemischte Produkt ist genau dann Null, wenn die Vektoren koplanar sind.

1. Bedingung für Koplanarität von Vektoren: Drei Vektoren sind genau dann koplanar, wenn ihr gemischtes Produkt Null ist.

§ Ein Vektortripel, das ein Paar kollinearer Vektoren enthält, ist koplanar.

§ Gemischtes Produkt koplanarer Vektoren. Dies ist ein Kriterium für die Koplanarität dreier Vektoren.

§ Koplanare Vektoren sind linear abhängig. Dies ist auch ein Kriterium für Koplanarität.

§ Es gibt reelle Zahlen wie z für koplanar, außer in den Fällen von oder. Dies ist eine Neuformulierung der bisherigen Eigenschaft und zugleich ein Kriterium der Koplanarität.

§ Im dreidimensionalen Raum bilden 3 nichtkoplanare Vektoren eine Basis. Das heißt, jeder Vektor kann in der Form dargestellt werden: . Dann werden sie Koordinaten in dieser Basis sein.

Das gemischte Produkt im rechten kartesischen Koordinatensystem (auf Orthonormalbasis) ist gleich der Determinante der aus Vektoren und zusammengesetzten Matrix:

§ 6. Allgemeine (vollständige) Gleichung der Ebene

wobei und Konstanten sind und gleichzeitig ungleich Null sind; in Vektorform:

Dabei ist der Radiusvektor des Punktes, der Vektor steht senkrecht zur Ebene (Normalvektor). Richtungskosinus Vektor:

Wenn einer der Koeffizienten in einer Ebenengleichung Null ist, wird die Gleichung aufgerufen unvollständig. Wenn die Ebene durch den Koordinatenursprung verläuft, wenn (oder , ) die Ebene parallel zur Achse (bzw. oder ) ist. Wenn ( , oder ) die Ebene parallel zur Ebene (bzw. oder ) ist.

§ Gleichung einer Ebene in Segmenten:

wobei , , die von der Ebene auf den Achsen und abgeschnittenen Segmente sind.

§ Gleichung einer Ebene, die durch einen Punkt geht senkrecht zum Normalenvektor :

in Vektorform:

(gemischtes Produkt von Vektoren), sonst

§ Normale (normalisierte) Ebenengleichung

§ Der Winkel zwischen zwei Ebenen. Wenn die Gleichungen von P. in der Form (1) angegeben sind, dann

Wenn in Vektorform, dann

§ Flugzeuge sind parallel, Wenn

Oder (Vektorprodukt)

§ Ebenen sind senkrecht, Wenn

Oder . (Skalarprodukt)

7. Gleichung einer Ebene, die durch drei gegebene Punkte verläuft , nicht auf derselben Geraden liegen:

8. Der Abstand von einem Punkt zu einer Ebene ist der kleinste der Abstände zwischen diesem Punkt und den Punkten der Ebene. Es ist bekannt, dass der Abstand von einem Punkt zu einer Ebene gleich der Länge der Senkrechten ist, die von diesem Punkt zur Ebene gezogen wird.

§ Punktabweichung aus der durch die normalisierte Gleichung gegebenen Ebene

Wenn und der Koordinatenursprung zusammen liegen verschiedene Seiten Flugzeug, sonst . Der Abstand von einem Punkt zu einer Ebene beträgt

§ Der Abstand vom Punkt zur durch die Gleichung angegebenen Ebene wird nach folgender Formel berechnet:

9. Ein Haufen Flugzeuge- Gleichung eines beliebigen Diagramms, das durch die Schnittlinie zweier Ebenen verläuft

Dabei sind α und β beliebige Zahlen, die nicht gleichzeitig Null sind.

Damit die drei durch sie definierten Ebenen allgemeine Gleichungen A 1 x+B 1 y+C 1 z+D 1 =0, A 2 x+B 2 y+C 2 z+D 2 =0, A 3 x+B 3 y+C 3 z+D 3 =0 In Bezug auf die PDSCs, die zu einem Bündel gehören, ob richtig oder uneigentlich, ist es notwendig und ausreichend, dass der Rang der Matrix entweder gleich zwei oder eins ist.
Satz 2. Es seien zwei Ebenen π 1 und π 2 in Bezug auf das PDSC durch ihre allgemeinen Gleichungen gegeben: A 1 x+B 1 y+C 1 z+D 1 =0, A 2 x+B 2 y+C 2 z+D 2 = 0. Damit die Ebene π 3, die relativ zum PDSC durch ihre allgemeine Gleichung A 3 x+B 3 y+C 3 z+D 3 =0 definiert ist, zu dem durch die Ebenen π 1 und π 2 gebildeten Strahl gehört, ist sie ist notwendig und ausreichend linke Seite Die Gleichungen der Ebene π 3 wurden als lineare Kombination der linken Seiten der Gleichungen der Ebenen π 1 und π 2 dargestellt.

10.Vektorparametrische Gleichung einer Linie im Weltraum:

Wo ist der Radiusvektor eines festen Punkts? M 0, das auf einer Linie liegt, ist ein Vektor ungleich Null, der kollinear zu dieser Linie ist, und ist der Radiusvektor eines beliebigen Punktes auf der Linie.

Parametrische Gleichung einer Geraden im Weltraum:

M

Kanonische Gleichung der Geraden im Weltraum:

Wo sind die Koordinaten eines festen Punktes? M 0 liegt auf einer geraden Linie; - Koordinaten des Vektors kollinear zu dieser Linie.

Allgemeine Vektorgleichung einer Geraden im Weltraum:

Da eine Gerade der Schnittpunkt zweier verschiedener nichtparalleler Ebenen ist, die jeweils durch die allgemeinen Gleichungen definiert werden:

dann kann die Gleichung der Geraden durch das System dieser Gleichungen angegeben werden:

Der Winkel zwischen den Richtungsvektoren beträgt gleich Winkel zwischen geraden Linien. Der Winkel zwischen Vektoren wird mithilfe des Skalarprodukts ermittelt. cosA=(ab)/IaI*IbI

Der Winkel zwischen einer Geraden und einer Ebene wird durch die Formel ermittelt:

Bedingungen für die Parallelität zweier Geraden:

a) Wenn die Geraden durch die Gleichungen (4) mit einem Winkelkoeffizienten gegeben sind, dann ist die notwendige und hinreichende Bedingung für ihre Parallelität die Gleichheit ihrer Winkelkoeffizienten:

k 1 = k 2 . (8)

b) Für den Fall, dass die Geraden durch die Gleichungen in gegeben sind Gesamtansicht(6) ist eine notwendige und hinreichende Bedingung für ihre Parallelität, dass die Koeffizienten für die entsprechenden aktuellen Koordinaten in ihren Gleichungen proportional sind, d. h.

Bedingungen für die Rechtwinkligkeit zweier Geraden:

a) Für den Fall, dass die Geraden durch die Gleichungen (4) mit einem Winkelkoeffizienten gegeben sind, ist eine notwendige und hinreichende Bedingung für ihre Rechtwinkligkeit, dass sie Pisten sind im Betrag umgekehrt und im Vorzeichen entgegengesetzt, d. h.

b) Wenn die Geradengleichungen in der allgemeinen Form (6) vorliegen, dann besteht die Bedingung für ihre Rechtwinkligkeit (notwendig und ausreichend) darin, die Gleichheit zu erfüllen

A 1 A 2 + B 1 B 2 = 0. (12)

Die Gerade heißt senkrecht zur Ebene, wenn es senkrecht zu einer Geraden in dieser Ebene steht. Wenn eine Linie senkrecht zu jeder von zwei Schnittlinien einer Ebene steht, dann ist sie senkrecht zu dieser Ebene. Damit eine Linie und eine Ebene parallel sind, ist es notwendig und ausreichend, dass der Normalenvektor zur Ebene und der Richtungsvektor der Linie senkrecht zueinander stehen. Dazu ist es notwendig, dass ihr Skalarprodukt gleich Null ist.

Damit eine Gerade und eine Ebene senkrecht zueinander stehen, ist es notwendig und ausreichend, dass der Normalenvektor zur Ebene und der Richtungsvektor der Geraden kollinear sind. Diese Bedingung ist erfüllt, wenn das Vektorprodukt dieser Vektoren gleich Null war.

12. Im Raum der Abstand von einem Punkt zu einer bestimmten Linie parametrische Gleichung

kann als Mindestabstand von einem gegebenen Punkt zu einem beliebigen Punkt auf einer Linie ermittelt werden. Koeffizient T Dieser Punkt kann durch die Formel gefunden werden

Abstand zwischen sich kreuzenden Linien heißt die Länge ihrer gemeinsamen Senkrechten. Er entspricht dem Abstand zwischen parallelen Ebenen, die durch diese Linien verlaufen.

Def. System der Elemente x 1,…,x m linear. pr-va V heißt linear abhängig, wenn ∃ λ 1 ,…, λ m ∈ ℝ (|λ 1 |+…+| λ m | ≠ 0) mit λ 1 x 1 +…+ λ m x m = θ .

Def. Ein System von Elementen x 1 ,…,x m ∈ V heißt linear unabhängig, wenn die Gleichheit λ 1 x 1 +…+ λ m x m = θ ⟹λ 1 =…= λ m =0 gilt.

Def. Ein Element x ∈ V heißt eine lineare Kombination von Elementen x 1 ,…,x m ∈ V, wenn ∃ λ 1 ,…, λ m ∈ ℝ mit x= λ 1 x 1 +…+ λ m x m .

Satz (lineares Abhängigkeitskriterium): Ein Vektorsystem x 1 ,…,x m ∈ V ist genau dann linear abhängig, wenn mindestens ein Vektor des Systems durch die anderen linear ausgedrückt wird.

Dok. Notwendigkeit: Sei x 1 ,…,x m linear abhängig ⟹ ∃ λ 1 ,…, λ m ∈ ℝ (|λ 1 |+…+| λ m | ≠ 0), so dass λ 1 x 1 +…+ λ m -1 x m -1 + λ m x m = θ. Nehmen wir also an, dass λ m ≠ 0 ist

x m = (- ) x 1 +…+ (- ) x m -1.

Angemessenheit: Mindestens einer der Vektoren sei linear durch die übrigen Vektoren ausgedrückt: x m = λ 1 x 1 +…+ λ m -1 x m -1 (λ 1 ,…, λ m -1 ∈ ℝ) λ 1 x 1 + …+ λ m -1 x m -1 +(-1) x m =0 λ m =(-1) ≠ 0 ⟹ x 1 ,…,x m - linear unabhängig.

Ven. lineare Abhängigkeitsbedingung:

Wenn ein System ein Nullelement oder ein linear abhängiges Teilsystem enthält, dann ist es linear abhängig.

λ 1 x 1 +…+ λ m x m = 0 – linear abhängiges System

1) Sei x 1 = θ, dann gilt diese Gleichheit für λ 1 =1 und λ 1 =…= λ m =0.

2) Sei λ 1 x 1 +…+ λ m x m =0 – linear abhängiges Teilsystem ⟹|λ 1 |+…+| λ m | ≠ 0 . Dann erhalten wir für λ 1 =0 auch |λ 1 |+…+| λ m | ≠ 0 ⟹ λ 1 x 1 +…+ λ m x m =0 – linear abhängiges System.

Basis des linearen Raums. Koordinaten des Vektors in einer bestimmten Basis. Koordinaten der Summen von Vektoren und des Produkts aus einem Vektor und einer Zahl. Eine notwendige und hinreichende Bedingung für die lineare Abhängigkeit eines Vektorsystems.

Definition: Ein geordnetes System von Elementen e 1, ..., e n eines linearen Raums V heißt Basis dieses Raums, wenn:

A) e 1 ... e n sind linear unabhängig

B) ∀ x ∈ α 1 … α n mit x= α 1 e 1 +…+ α n e n

x= α 1 e 1 +…+ α n e n – Entwicklung des Elements x in der Basis e 1, …, e n

α 1 … α n ∈ ℝ – Koordinaten des Elements x in der Basis e 1, …, e n

Satz: Wenn eine Basis e 1, …, e n in einem linearen Raum V gegeben ist, dann ist ∀ x ∈ V die Koordinatenspalte x in der Basis e 1, …, e n eindeutig bestimmt (die Koordinaten sind eindeutig bestimmt)

Nachweisen: Sei x=α 1 e 1 +…+ α n e n und x=β 1 e 1 +…+β n e n

x= ⇔ = Θ, d.h. e 1, …, e n sind linear unabhängig, dann - =0 ∀ i=1, …, n ⇔ = ∀ i=1, …, n usw.

Satz: Sei e 1, …, e n die Basis des linearen Raums V; x, y sind beliebige Elemente des Raumes V, λ ∈ ℝ ist eine beliebige Zahl. Wenn x und y addiert werden, werden ihre Koordinaten addiert; wenn x mit λ multipliziert wird, werden auch die x-Koordinaten mit λ multipliziert.

Nachweisen: x= (e 1, …, e n) und y= (e 1, …, e n)

x+y= + = (e 1, …, e n)

λx= λ ) = (e 1, …, e n)

Lemma1: (notwendige und hinreichende Bedingung für die lineare Abhängigkeit eines Vektorsystems)

Sei e 1 …е n die Basis des Raumes V. Ein System von Elementen f 1 , …, f k ∈ V ist genau dann linear abhängig, wenn die Koordinatenspalten dieser Elemente in der Basis e 1, …, e n sind linear abhängig

Nachweisen: Erweitern wir f 1, …, f k gemäß der Basis e 1, …, e n

f m =(e 1, …, e n) m=1, …, k

λ 1 f 1 +…+λ k f k =(e 1, …, e n)[ λ 1 +…+ λ n ], also λ 1 f 1 +…+λ k f k = Θ ⇔

⇔ λ 1 +…+ λ n = was bewiesen werden musste.

13. Dimension des linearen Raums. Satz über den Zusammenhang zwischen Dimension und Basis.
Definition: Ein linearer Raum V heißt n-dimensionaler Raum, wenn es n linear unabhängige Elemente in V gibt und ein System aus n+1 beliebigen Elementen des Raums V linear abhängig ist. In diesem Fall heißt n die Dimension des linearen Raums V und wird mit dimV=n bezeichnet.

Ein linearer Raum heißt unendlichdimensional, wenn ∀N ∈ ℕ im Raum V ein linear unabhängiges System mit N Elementen existiert.

Satz: 1) Wenn V ein n-dimensionaler linearer Raum ist, dann bildet jedes geordnete System von n linear unabhängigen Elementen dieses Raums eine Basis. 2) Wenn es in einem linearen Raum V eine Basis gibt, die aus n Elementen besteht, dann ist die Dimension von V gleich n (dimV=n).

Nachweisen: 1) Sei dimV=n ⇒ in V ∃ n linear unabhängige Elemente e 1, …, e n. Wir werden beweisen, dass diese Elemente eine Basis bilden, das heißt, wir werden beweisen, dass ∀ x ∈ V in e 1, …, e n entwickelt werden kann. Fügen wir ihnen x hinzu: e 1, ..., e n, x – dieses System enthält n+1 Vektoren, was bedeutet, dass es linear abhängig ist. Da e 1, …, e n linear unabhängig ist, gilt nach Satz 2 X linear ausgedrückt durch e 1, …, e n d.h. ∃ ,…, so dass x= α 1 e 1 +…+ α n e n . Also ist e 1, …, e n die Basis des Raumes V. 2) Sei e ​​1, …, e n die Basis von V, also gibt es ∃ n linear unabhängige Elemente in V. Nehmen wir beliebige f 1 ,…,f n ,f n +1 ∈ V – n+1 Elemente. Zeigen wir ihre lineare Abhängigkeit. Lassen Sie uns sie nach ihrer Grundlage aufschlüsseln:

f m =(e 1, …,e n) = wobei m = 1,…,n Erstellen wir eine Matrix aus Koordinatenspalten: A= Die Matrix enthält n Zeilen ⇒ RgA≤n. Anzahl der Spalten n+1 > n ≥ RgA ⇒ Spalten der Matrix A (d. h. Spalten mit Koordinaten f 1 ,…,f n ,f n +1) sind linear abhängig. Aus Lemma 1 ⇒ ,…,f n ,f n +1 sind linear abhängig ⇒ dimV=n.

Folge: Wenn eine Basis n Elemente enthält, enthält jede andere Basis in diesem Raum n Elemente.

Satz 2: Wenn das Vektorsystem x 1 ,… ,x m -1 , x m linear abhängig ist und sein Teilsystem x 1 ,… ,x m -1 linear unabhängig ist, dann wird x m linear durch x 1 ,… ,x m -1 ausgedrückt

Nachweisen: Weil x 1 ,… ,x m -1 , x m ist linear abhängig, dann ∃ , …, , ,

, …, | , | so dass. Wenn , , …, | => x 1 ,… ,x m -1 – sind linear unabhängig, was nicht sein kann. Das bedeutet m = (- ) x 1 +…+ (- ) x m -1.