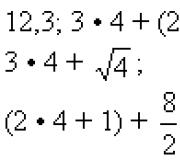Darstellung natürlicher Zahlen durch Punkte auf einem Zahlenstrahl. Zahlenmodul (Absolutwert der Zahl), Definitionen, Beispiele, Eigenschaften

Wir wissen bereits, dass die Menge der reellen Zahlen $R$ aus rationalen und irrationalen Zahlen besteht.

Rationale Zahlen können immer als Dezimalzahlen (endlich oder unendlich periodisch) dargestellt werden.

Irrationale Zahlen werden als unendliche, aber nicht wiederkehrende Dezimalzahlen geschrieben.

Die Menge der reellen Zahlen $R$ enthält auch die Elemente $-\infty $ und $+\infty $, für die die Ungleichungen $-\infty

Überlegen Sie, wie Sie reelle Zahlen darstellen können.

Gemeinsame Brüche

Gewöhnliche Brüche werden mit zwei natürlichen Zahlen und einem horizontalen Bruchstrich geschrieben. Der Bruchstrich ersetzt eigentlich das Divisionszeichen. Die Zahl unter dem Strich ist der Nenner (Teiler), die Zahl über dem Strich ist der Zähler (Teiler).

Definition

Ein Bruch heißt echt, wenn sein Zähler kleiner als sein Nenner ist. Umgekehrt heißt ein Bruch unecht, wenn sein Zähler größer oder gleich seinem Nenner ist.

Für gewöhnliche Brüche gibt es einfache, praktisch naheliegende Vergleichsregeln ($m$,$n$,$p$ sind natürliche Zahlen):

von zwei Brüchen mit gleichem Nenner ist der mit dem größeren Zähler größer, also $\frac(m)(p) >\frac(n)(p) $ für $m>n$;
von zwei Brüchen mit gleichem Zähler ist der mit dem kleineren Nenner größer, also $\frac(p)(m) >\frac(p)(n) $ für $ m
ein echter Bruch ist immer kleiner als eins; unechter Bruch ist immer größer als eins; ein Bruch, dessen Zähler gleich dem Nenner ist, ist gleich eins;
Jeder unechte Bruch ist größer als jeder echte Bruch.

Dezimal Zahlen

Die Schreibweise einer Dezimalzahl (Dezimalbruch) hat die Form: ganzzahliger Teil, Dezimalpunkt, Bruchteil. Die Dezimalschreibweise eines gewöhnlichen Bruchs erhält man, indem man den "Winkel" des Zählers durch den Nenner dividiert. Dies kann entweder zu einem endlichen Dezimalbruch oder einem unendlichen periodischen Dezimalbruch führen.

Definition

Die Nachkommastellen heißen Nachkommastellen. In diesem Fall wird die erste Ziffer nach dem Dezimalpunkt als Zehntelziffer bezeichnet, die zweite als Hundertstelziffer, die dritte als Tausendstelziffer usw.

Beispiel 1

Wir ermitteln den Wert der Dezimalzahl 3,74. Wir erhalten: $3,74=3+\frac(7)(10) +\frac(4)(100) $.

Die Dezimalzahl kann gerundet werden. In diesem Fall müssen Sie die Stelle angeben, auf die gerundet wird.

Die Rundungsregel lautet wie folgt:

alle Ziffern rechts von dieser Ziffer werden durch Nullen ersetzt (wenn diese Ziffern vor dem Komma stehen) oder verworfen (wenn diese Ziffern nach dem Komma stehen);
Wenn die erste Ziffer nach der angegebenen Ziffer kleiner als 5 ist, wird die Ziffer dieser Ziffer nicht geändert.
Wenn die erste Ziffer nach der angegebenen Ziffer 5 oder mehr ist, wird die Ziffer dieser Ziffer um eins erhöht.

Beispiel 2

Runden wir die Zahl 17302 auf das nächste Tausend: 17000.
Runden wir die Zahl 17378 auf die nächsten Hunderter: 17400.
Runden wir die Zahl 17378,45 auf Zehner: 17380.
Runden wir die Zahl 378,91434 auf das nächste Hundertstel: 378,91.
Runden wir die Zahl 378,91534 auf das nächste Hundertstel: 378,92.

Umwandlung einer Dezimalzahl in einen gewöhnlichen Bruch.

Fall 1

Eine Dezimalzahl ist eine abschließende Dezimalzahl.

Die Konvertierungsmethode wird im folgenden Beispiel gezeigt.

Beispiel 2

Wir haben: $3,74=3+\frac(7)(10) +\frac(4)(100) $.

Reduzieren Sie auf einen gemeinsamen Nenner und erhalten Sie:

Der Bruch kann gekürzt werden: $3,74=\frac(374)(100) =\frac(187)(50) $.

Fall 2

Eine Dezimalzahl ist eine unendlich wiederkehrende Dezimalzahl.

Das Transformationsverfahren beruht darauf, dass der periodische Teil eines periodischen Dezimalbruchs als Summe der Glieder einer unendlich fallenden geometrischen Folge betrachtet werden kann.

Beispiel 4

$0,\left(74\right)=\frac(74)(100) +\frac(74)(10000) +\frac(74)(1000000) +\ldots $. Das erste Glied der Progression ist $a=0.74$, der Nenner der Progression ist $q=0.01$.

Beispiel 5

$0.5\left(8\right)=\frac(5)(10) +\frac(8)(100) +\frac(8)(1000) +\frac(8)(10000) +\ldots $ . Das erste Glied der Progression ist $a=0.08$, der Nenner der Progression ist $q=0.1$.

Die Summe der Glieder einer unendlich fallenden geometrischen Folge wird durch die Formel $s=\frac(a)(1-q) $ berechnet, wobei $a$ das erste Glied und $q$ der Nenner der Folge $ ist \links (0

Beispiel 6

Konvertieren wir den unendlichen periodischen Dezimalbruch $0,\left(72\right)$ in einen regulären.

Das erste Glied der Progression ist $a=0.72$, der Nenner der Progression ist $q=0.01$. Wir erhalten: $s=\frac(a)(1-q) =\frac(0.72)(1-0.01) =\frac(0.72)(0.99) =\frac(72)( 99) =\frac(8). )(11) $. Also $0,\left(72\right)=\frac(8)(11) $.

Beispiel 7

Lassen Sie uns den unendlichen periodischen Dezimalbruch $0.5\left(3\right)$ in einen regulären Bruch umwandeln.

Das erste Glied der Progression ist $a=0.03$, der Nenner der Progression ist $q=0.1$. Wir erhalten: $s=\frac(a)(1-q) =\frac(0.03)(1-0.1) =\frac(0.03)(0.9) =\frac(3)( 90) =\frac(1). )(30)$.

Also $0,5\left(3\right)=\frac(5)(10) +\frac(1)(30) =\frac(5\cdot 3)(10\cdot 3) +\frac( 1)(30 ) =\frac(15)(30) +\frac(1)(30) =\frac(16)(30) =\frac(8)(15) $.

Reelle Zahlen lassen sich durch Punkte auf dem Zahlenstrahl darstellen.

In diesem Fall nennen wir die numerische Achse eine unendliche Linie, auf der der Ursprung (Punkt $O$), die positive Richtung (angezeigt durch einen Pfeil) und die Skalierung (zur Anzeige von Werten) ausgewählt werden.

Zwischen allen reellen Zahlen und allen Punkten der Zahlenachse besteht eine Eins-zu-Eins-Beziehung: Jeder Punkt entspricht einer einzelnen Zahl und umgekehrt entspricht jede Zahl einem einzelnen Punkt. Daher ist die Menge der reellen Zahlen ebenso stetig und unendlich wie der Zahlenstrahl stetig und unendlich ist.

Einige Teilmengen der Menge der reellen Zahlen werden numerische Intervalle genannt. Die Elemente eines numerischen Intervalls sind Zahlen $x\in R$, die eine bestimmte Ungleichung erfüllen. Seien $a\in R$, $b\in R$ und $a\le b$. In diesem Fall können die Arten von Lücken wie folgt sein:

Intervall $\left(a,\; b\right)$. Gleichzeitig $ a
Segment $\left$. Außerdem $a\le x\le b$.
Halbsegmente oder Halbintervalle $\left$. Gleichzeitig $ a \le x
Unendliche Spannen, zB $a

Von großer Bedeutung ist auch eine Art Intervall, die sogenannte Nachbarschaft eines Punktes. Die Umgebung eines gegebenen Punktes $x_(0) \in R$ ist ein beliebiges Intervall $\left(a,\; b\right)$, das diesen Punkt in sich enthält, also $a 0$ - 10. Radius.

Der absolute Wert der Zahl

Der Absolutwert (oder Modulus) einer reellen Zahl $x$ ist eine nicht negative reelle Zahl $\left|x\right|$, definiert durch die Formel: $\left|x\right|=\left\(\ begin(array)(c) (\; \; x\; \; (\rm on)\; \; x\ge 0) \\ (-x\; \; (\rm on)\; \; x

Geometrisch bedeutet $\left|x\right|$ den Abstand zwischen den Punkten $x$ und 0 auf der reellen Achse.

Eigenschaften von Absolutwerten:

aus der Definition folgt, dass $\left|x\right|\ge 0$, $\left|x\right|=\left|-x\right|$;
für den Betrag der Summe und für den Betrag der Differenz zweier Zahlen die Ungleichungen $\left|x+y\right|\le \left|x\right|+\left|y\right|$, $\ left|x-y\right|\le \left|x\right|+\left|y\right|$ und auch $\left|x+y\right|\ge \left|x\right|-\left|y \right|$,$\ left|x-y\right|\ge \left|x\right|-\left|y\right|$;
der Betrag des Produkts und der Betrag des Quotienten zweier Zahlen erfüllen die Gleichungen $\left|x\cdot y\right|=\left|x\right|\cdot \left|y\right|$ und $\left |\frac(x)( y) \right|=\frac(\left|x\right|)(\left|y\right|) $.

Ausgehend von der Definition des Betrages für eine beliebige Zahl $a>0$ kann man auch die Äquivalenz folgender Ungleichungspaare feststellen:

wenn $ \links|x\rechts|
if $\left|x\right|\le a$ then $-a\le x\le a$;
wenn $\left|x\right|>a$ dann entweder $xa$;
wenn $\left|x\right|\ge a$, dann entweder $x\le -a$ oder $x\ge a$.

Beispiel 8

Lösen Sie die Ungleichung $\left|2\cdot x+1\right|

Diese Ungleichung entspricht den Ungleichungen $-7

Von hier erhalten wir: $-8

Ein Zahlenstrahl, eine Zahlenachse, ist eine Linie, auf der reelle Zahlen dargestellt werden. Auf der geraden Linie wird der Ursprung gewählt - der Punkt O (Punkt O steht für 0) und der Punkt L, der die Einheit darstellt. Der Punkt L steht normalerweise rechts vom Punkt O. Die Strecke OL wird Einheitsstrecke genannt.

Die Punkte rechts vom Punkt O repräsentieren positive Zahlen. Punkte links vom Punkt. Oh, stellen Sie negative Zahlen dar. Wenn der Punkt X eine positive Zahl x darstellt, dann ist der Abstand OX = x. Wenn der Punkt X eine negative Zahl x darstellt, dann ist der Abstand OX = - x.

Die Zahl, die die Lage eines Punktes auf einer Geraden angibt, heißt Koordinate dieses Punktes.

Der in der Figur gezeigte Punkt V hat eine Koordinate von 2, und Punkt H hat eine Koordinate von –2,6.

Der Betrag einer reellen Zahl ist der Abstand vom Ursprung zum Punkt, der dieser Zahl entspricht. Bezeichne den Betrag der Zahl x, also: | x |. Offensichtlich | 0 | = 0.

Wenn die Zahl x größer als 0 ist, dann | x | = x, und wenn x kleiner als 0 ist, dann | x | = -x. Auf diesen Eigenschaften des Moduls basiert die Lösung vieler Gleichungen und Ungleichungen mit dem Modul.

Beispiel: Gleichung lösen | x-3 | = 1.

Lösung: Betrachten Sie zwei Fälle – den ersten Fall, wenn x -3 > 0, und den zweiten Fall, wenn x - 3 0 ist.

1. x - 3 > 0, x > 3.

In diesem Fall | x-3 | = x - 3.

Die Gleichung hat die Form x - 3 \u003d 1, x \u003d 4. 4\u003e 3 - erfüllen die erste Bedingung.

2. x -3 0, x 3.

In diesem Fall | x-3 | = - x + 3

Die Gleichung hat die Form x + 3 \u003d 1, x \u003d - 2. -2 3 - erfüllt die zweite Bedingung.

Antwort: x = 4, x = -2.

Numerische Ausdrücke.

Ein numerischer Ausdruck ist eine Sammlung von einer oder mehreren Zahlen und Funktionen, die durch arithmetische Operatoren und Klammern verbunden sind.
Beispiele für numerische Ausdrücke:

Der Wert eines numerischen Ausdrucks ist eine Zahl.
Operationen in numerischen Ausdrücken werden in der folgenden Reihenfolge ausgeführt:

1. Aktionen in Klammern.

2. Berechnung von Funktionen.

3. Potenzierung

4. Multiplikation und Division.

5. Addition und Subtraktion.

6. Operationen des gleichen Typs werden von links nach rechts ausgeführt.

Der Wert des ersten Ausdrucks ist also die Zahl selbst 12.3
Um den Wert des zweiten Ausdrucks zu berechnen, führen wir die Aktionen in der folgenden Reihenfolge aus:

1. Führen Sie die Aktionen in Klammern in der folgenden Reihenfolge aus - zuerst erhöhen wir 2 in die dritte Potenz und subtrahieren dann 11 von der resultierenden Zahl:

3 4 + (23 - 11) = 3 4 + (8 - 11) = 3 4 + (-3)

2. Multipliziere 3 mit 4:

3 4 + (-3) = 12 + (-3)

3. Führen Sie die Vorgänge nacheinander von links nach rechts aus:

12 + (-3) = 9.
Ein Ausdruck mit Variablen ist eine Sammlung von einer oder mehreren Zahlen, Variablen und Funktionen, die durch arithmetische Operatoren und Klammern verbunden sind. Die Werte von Ausdrücken mit Variablen hängen von den Werten der darin enthaltenen Variablen ab. Die Reihenfolge der Operationen ist hier die gleiche wie bei numerischen Ausdrücken. Manchmal ist es nützlich, Ausdrücke mit Variablen zu vereinfachen, indem verschiedene Aktionen ausgeführt werden - Klammern, Klammererweiterung, Gruppierung, Kürzung von Brüchen, Kürzung ähnlicher Brüche usw. Um Ausdrücke zu vereinfachen, werden häufig verschiedene Formeln verwendet, z. B. abgekürzte Multiplikationsformeln, Eigenschaften verschiedener Funktionen usw.

Algebraische Ausdrücke.

Ein algebraischer Ausdruck ist eine oder mehrere algebraische Größen (Zahlen und Buchstaben), die durch Zeichen algebraischer Operationen miteinander verbunden sind: Addition, Subtraktion, Multiplikation und Division sowie das Ziehen der Wurzel und das Erhöhen auf eine ganzzahlige Potenz (außerdem müssen die Wurzel und der Exponent unbedingt erforderlich sein ganze Zahlen sein) und Zeichen der Abfolge dieser Aktionen (normalerweise Klammern verschiedener Art). Die Anzahl der im algebraischen Ausdruck enthaltenen Werte muss endlich sein.

Ein Beispiel für einen algebraischen Ausdruck:

"Algebraischer Ausdruck" ist ein syntaktisches Konzept, dh etwas ist genau dann ein algebraischer Ausdruck, wenn es bestimmten grammatikalischen Regeln gehorcht (siehe Formale Grammatik). Wenn die Buchstaben in einem algebraischen Ausdruck als Variablen betrachtet werden, erhält der algebraische Ausdruck die Bedeutung einer algebraischen Funktion.

Nr. 1. Eigenschaften rationaler Zahlen.

 Ordentlichkeit . Für alle rationalen Zahlen gibt es eine Regel, die es Ihnen ermöglicht, zwischen ihnen eine und nur eine der drei eindeutig zu identifizieren Beziehungen: "", "" oder "". Diese Regel heißt Ordnungsregel und wird wie folgt formuliert: Zwei positive Zahlen sind durch dieselbe Beziehung verbunden wie zwei ganze Zahlen; zwei nicht positive Zahlen und sind durch die gleiche Beziehung miteinander verbunden wie zwei nicht negative Zahlen und; wenn plötzlich nicht negativ, sondern negativ, dann.

Summierung von Brüchen

 Additionsoperation . Summationsregel, was sie in Übereinstimmung mit einer rationalen Zahl bringt . In diesem Fall wird die Nummer selbst angerufen Summe Zahlen u wird bezeichnet, und der Prozess, eine solche Zahl zu finden, wird aufgerufen Summe. Die Summationsregel hat folgende Form: .

 Multiplikationsoperation . Für alle rationalen Zahlen und gibt es eine sogenannte Multiplikationsregel, was sie in Übereinstimmung mit einer rationalen Zahl bringt . In diesem Fall wird die Nummer selbst angerufen Arbeit Nummern ii wird bezeichnet, und der Prozess zum Auffinden einer solchen Nummer wird auch genannt Multiplikation. Die Multiplikationsregel lautet wie folgt: .

 Transitivität Ordnungsbeziehungen. Für jedes Tripel von rationalen Zahlen, und wenn immer weniger, dann weniger, und wenn gleich und gleich, dann gleich.

 Kommutativität Zusatz. Bei einem Wechsel der Stellen rationaler Terme ändert sich die Summe nicht.

 Assoziativität Zusatz. Die Reihenfolge, in der drei rationale Zahlen addiert werden, hat keinen Einfluss auf das Ergebnis.

 VerfügbarkeitNull . Es gibt eine rationale Zahl 0, die alle anderen rationalen Zahlen erhält, wenn sie summiert werden.

 Das Vorhandensein von Gegenzahlen. Jede rationale Zahl hat eine entgegengesetzte rationale Zahl, die summiert 0 ergibt.

 Kommutativität der Multiplikation. Indem die Plätze der rationalen Faktoren geändert werden, ändert sich das Produkt nicht.

 Assoziativität der Multiplikation. Die Reihenfolge, in der drei rationale Zahlen multipliziert werden, hat keinen Einfluss auf das Ergebnis.

 VerfügbarkeitEinheiten . Es gibt eine rationale Zahl 1, die bei Multiplikation jede andere rationale Zahl erhält.

 Verfügbarkeitreziproke Zahlen . Jede rationale Zahl ungleich Null hat eine inverse rationale Zahl, deren Multiplikation 1 ergibt.

 Distributivität Multiplikation in Bezug auf Addition. Die Multiplikationsoperation ist konsistent mit der Additionsoperation durch das Verteilungsgesetz:

 Zusammenhang der Ordnungsbeziehung mit der Additionsoperation. Dieselbe rationale Zahl kann zur linken und rechten Seite einer rationalen Ungleichung addiert werden.

 Zusammenhang der Ordnungsbeziehung mit der Operation der Multiplikation. Die linke und die rechte Seite einer rationalen Ungleichung können mit derselben positiven rationalen Zahl multipliziert werden.

 Axiom von Archimedes . Unabhängig von der rationalen Zahl können Sie so viele Einheiten nehmen, dass ihre Summe überschritten wird.

Nr. 2. Modul einer reellen Zahl.

Definition . Der Betrag einer nicht negativen reellen Zahl x ist die Zahl selbst: | x | = x; der Betrag einer negativen reellen Zahl x ist die entgegengesetzte Zahl: I x | = -x.

Kurz gesagt wird es so geschrieben:

2. Die geometrische Bedeutung des Moduls einer reellen Zahl

Kehren wir zur Menge R der reellen Zahlen und ihrer Geometrie zurück Modelle- Zahlenreihe. Wir markieren zwei Punkte a und b auf der Linie (zwei reelle Zahlen a und b) und bezeichnen mit (a, b) den Abstand zwischen den Punkten a und b (- der Buchstabe des griechischen Alphabets "ro"). Dieser Abstand ist gleich b - a, wenn b > a (Abb. 101), er ist gleich a - b, wenn a > b (Abb. 102), schließlich ist er Null, wenn a = b.

Alle drei Fälle werden durch eine Formel abgedeckt:

b) Gleichung | x + 3,2 | = 2 umschreiben in der Form | x - (- 3,2) | \u003d 2 und weiter (x, - 3,2) \u003d 2. Es gibt zwei Punkte auf der Koordinatenlinie, die vom Punkt - 3,2 in einem Abstand von 2 entfernt sind. Dies sind die Punkte - 5,2 und - 1,2 (Abb. . 104). Die Gleichung hat also zwei Wurzel: -5,2 und -1,2.

№4.SATZ VON REALEN ZAHLEN

Die Vereinigung der Menge der rationalen Zahlen mit der Menge der irrationalen Zahlen heißt Menge gültig (oder Material ) Zahlen . Die Menge der reellen Zahlen wird durch das Symbol bezeichnet R. Offensichtlich, .

Reelle Zahlen werden angezeigt numerische Achse Oh Punkte (Abb.). Dabei entspricht jede reelle Zahl einem bestimmten Punkt der Zahlenachse und jeder Punkt der Achse einer bestimmten reellen Zahl.

Daher können Sie anstelle der Wörter "reelle Zahl" "Punkt" sagen.

Nr. 5. Nummer Lücken.

Lückentyp	geometrische Bilder	Bezeichnung	Schreiben mit Ungleichungen
Intervall

Halbe Pause
Halbe Pause


offener Strahl
offener Strahl

Nr. 6. Numerische Funktion.

Lassen Sie sich eine Zahlenmenge geben, wenn jeder Zahl eine einzelne Zahl zugeordnet ist j, dann sagen wir das am Set D numerisch Funktion :

j = f (x),

Ein Haufen D namens Funktionsumfang und bezeichnet D (f (x)). Die Menge aller Elemente f (x), wo heißt Funktionsumfang und bezeichnet E (f (x)).

Anzahl x rufe oft an Funktionsargument oder eine unabhängige Variable und die Zahl j- abhängige Variable oder tatsächlich Funktion Variable x. Die dem Wert entsprechende Nummer wird angerufen Funktionswert an einem Punkt und bezeichnen oder

Zum Einstellen einer Funktion f, müssen Sie Folgendes angeben:

1) seinen Definitionsbereich D (f (x));

2) Geben Sie die Regel an f, wonach jedem Wert ein Wert zugeordnet ist j = f (x).

№7. Umkehrfunktion,

Umkehrfunktion

Wenn die Rollen von Argument und Funktion vertauscht sind, dann x wird eine Funktion von j. In diesem Fall spricht man von einer neuen aufgerufenen Funktion Umkehrfunktion. Angenommen, wir haben eine Funktion:

v = u 2 ,

wo u- Argument, a v- Funktion. Wenn wir ihre Rollen vertauschen, bekommen wir u als eine Funktion v :

Wenn wir das Argument in beiden Funktionen als bezeichnen x , und die Funktion durch j, dann haben wir zwei Funktionen:

jedes davon ist das Inverse des anderen.

BEISPIELE. Diese Funktionen sind zueinander invers:

1) Sünde x und arcsin x, denn wenn j= Sünde x, dann x= Arcsin j;

2) weil x und Arcco x, denn wenn j= cos x, dann x= Arkkos j;

3) braun x und Arctan x, denn wenn j= braun x, dann x= Arctan j;

4) e x und ln x, denn wenn j= e x, dann x=ln j.

Inverse trigonometrische Funktionen- mathematische Funktionen, die invers zu trigonometrischen Funktionen sind. Inverse trigonometrische Funktionen umfassen normalerweise sechs Funktionen:

Arkussinus(Symbol: arcsin)

Arkuskosinus(Symbol: arccos)

Bogentangente(Bezeichnung: arctg; in der ausländischen Literatur arctan)

Bogentangente(Bezeichnung: arcctg; in der ausländischen Literatur arccotan)

Bogensekant(Symbol: Bogensekunden)

Arkuskosekan(Bezeichnung: arccosec; in der ausländischen Literatur arccsc)

№8. Grundlegende elementare Funktionen. Elementare Funktionen

Es ist erwähnenswert, dass die inversen trigonometrischen Funktionen mehrwertig (unendlich signifikant) sind, wenn mit ihnen gearbeitet wird, werden die sogenannten Hauptwerte verwendet.

№9. Komplexe Zahlen

werden geschrieben als: ein+ Bi. Hier a und b – reale Nummern, a ich – imaginäre Einheit, d.h. ich 2 = –1. Anzahl a namens Abszisse, a b – Ordinate komplexe Zahl ein+ Bi. Zwei komplexe Zahlen ein+ Bi und a – Bi namens konjugieren komplexe Zahlen.

Reelle Zahlen können durch Punkte auf einer geraden Linie dargestellt werden, wie in der Abbildung gezeigt, wobei Punkt A die Zahl 4 und Punkt B -5 darstellt. Dieselben Zahlen können auch durch Segmente OA, OB dargestellt werden, wobei nicht nur ihre Länge, sondern auch ihre Richtung berücksichtigt werden.

Jeder Punkt M des Zahlenstrahls stellt eine reelle Zahl dar (rational, wenn das Segment OM mit einer Längeneinheit kommensurabel ist, und irrational, wenn es inkommensurabel ist). Auf dem Zahlenstrahl ist also kein Platz für komplexe Zahlen.

Aber komplexe Zahlen können auf der Zahlenebene dargestellt werden. Dazu wählen wir ein rechteckiges Koordinatensystem in der Ebene, mit gleichem Maßstab auf beiden Achsen.

Komplexe Zahl a + b ich dargestellt durch den Punkt M, in dem die Abszisse x gleich der Abszisse ist a komplexe Zahl, und die Ordinate von y ist gleich der Ordinate b komplexe Zahl.

In diesem Artikel werden wir im Detail analysieren der Absolutwert einer Zahl. Wir geben verschiedene Definitionen des Moduls einer Zahl, führen die Notation ein und geben grafische Illustrationen. In diesem Fall betrachten wir verschiedene Beispiele für das Finden des Moduls einer Zahl per Definition. Danach listen wir die Haupteigenschaften des Moduls auf und begründen sie. Am Ende des Artikels werden wir darüber sprechen, wie der Modul einer komplexen Zahl bestimmt und gefunden wird.

Seitennavigation.

Zahlenmodul - Definition, Notation und Beispiele

Zuerst stellen wir vor Modulbezeichnung. Das Modul der Zahl a wird als geschrieben, d. h. links und rechts der Zahl setzen wir vertikale Linien, die das Zeichen des Moduls bilden. Lassen Sie uns ein paar Beispiele geben. Beispielsweise kann modulo -7 geschrieben werden als ; Modul 4.125 wird geschrieben als und Modul wird geschrieben als .

Die folgende Definition des Moduls bezieht sich auf und daher auf und auf ganze Zahlen und auf rationale und irrationale Zahlen als Bestandteile der Menge reeller Zahlen. Wir werden über den Modul einer komplexen Zahl in sprechen.

Definition.

Modul von a ist entweder die Zahl a selbst, falls a eine positive Zahl ist, oder die Zahl −a, das Gegenteil der Zahl a, falls a eine negative Zahl ist, oder 0, falls a=0 .

Die stimmhafte Definition des Moduls einer Zahl wird oft in der folgenden Form geschrieben , bedeutet diese Notation, dass wenn a>0 , wenn a=0 und wenn a<0 .

Der Datensatz kann kompakter dargestellt werden . Diese Notation bedeutet, dass wenn (a größer oder gleich 0 ist) und wenn a<0 .

Es gibt auch einen Rekord . Hier sollte der Fall a = 0 separat erläutert werden. In diesem Fall haben wir , aber −0=0 , da Null als eine Zahl angesehen wird, die sich selbst entgegengesetzt ist.

Lassen Sie uns bringen Beispiele für die Ermittlung des Moduls einer Zahl mit vorgegebener Definition. Lassen Sie uns zum Beispiel Module mit den Nummern 15 und . Beginnen wir mit der Suche. Da die Zahl 15 positiv ist, ist ihr Modul per Definition gleich dieser Zahl selbst, also . Was ist der Modul einer Zahl? Da eine negative Zahl ist, ist ihr Modul gleich der Zahl, die der Zahl entgegengesetzt ist, dh der Zahl . Auf diese Weise, .

Zum Abschluss dieses Absatzes geben wir eine Schlussfolgerung, die in der Praxis sehr praktisch anzuwenden ist, wenn der Modul einer Zahl ermittelt wird. Aus der Definition des Moduls einer Zahl folgt das Der Modul einer Zahl ist gleich der Zahl unter dem Vorzeichen des Moduls, unabhängig von ihrem Vorzeichen, und aus den oben diskutierten Beispielen ist dies sehr deutlich ersichtlich. Die stimmhafte Aussage erklärt, warum der Modul einer Zahl auch genannt wird der Absolutwert der Zahl. Der Betrag einer Zahl und der Betrag einer Zahl sind also ein und dasselbe.

Modul einer Zahl als Abstand

Geometrisch kann der Modul einer Zahl interpretiert werden als Distanz. Lassen Sie uns bringen Bestimmung des Moduls einer Zahl in Bezug auf die Entfernung.

Definition.

Modul von a ist der Abstand vom Ursprung auf der Koordinatenlinie zu dem Punkt, der der Zahl a entspricht.

Diese Definition stimmt mit der im ersten Absatz gegebenen Definition des Moduls einer Zahl überein. Lassen Sie uns diesen Punkt erklären. Der Abstand vom Ursprung zum Punkt, der einer positiven Zahl entspricht, ist gleich dieser Zahl. Null entspricht dem Ursprung, also ist der Abstand vom Ursprung zum Punkt mit der Koordinate 0 gleich Null (kein einzelnes Segment und kein Segment, das einen Bruchteil des Einheitssegments ausmacht, muss verschoben werden, um von Punkt O zu dem Punkt zu gelangen mit Koordinate 0). Die Entfernung vom Ursprung zu einem Punkt mit negativer Koordinate ist gleich der Zahl gegenüber der Koordinate des gegebenen Punktes, da sie gleich der Entfernung vom Ursprung zu dem Punkt ist, dessen Koordinate die entgegengesetzte Zahl ist.

Beispielsweise ist der Modul der Zahl 9 gleich 9, da der Abstand vom Ursprung zum Punkt mit der Koordinate 9 gleich neun ist. Nehmen wir ein anderes Beispiel. Der Punkt mit der Koordinate −3,25 hat einen Abstand von 3,25 vom Punkt O, also .

Die klingende Definition des Betrags einer Zahl ist ein Sonderfall der Definition des Betrags der Differenz zweier Zahlen.

Definition.

Differenzmodul zweier Zahlen a und b ist gleich dem Abstand zwischen den Punkten der Koordinatenlinie mit den Koordinaten a und b .

Das heißt, wenn Punkte auf der Koordinatenlinie A(a) und B(b) gegeben sind, dann ist der Abstand von Punkt A zu Punkt B gleich dem Betrag der Differenz zwischen den Zahlen a und b. Wenn wir den Punkt O (Referenzpunkt) als Punkt B nehmen, erhalten wir die Definition des Moduls der Zahl, die am Anfang dieses Absatzes angegeben ist.

Bestimmen des Moduls einer Zahl durch die arithmetische Quadratwurzel

Manchmal gefunden Bestimmung des Moduls durch die arithmetische Quadratwurzel.

Lassen Sie uns zum Beispiel die Module der Zahlen −30 und basierend auf dieser Definition berechnen. Wir haben . In ähnlicher Weise berechnen wir den Modul von zwei Dritteln: .

Die Definition des Moduls einer Zahl in Bezug auf die arithmetische Quadratwurzel stimmt auch mit der Definition im ersten Absatz dieses Artikels überein. Zeigen wir es. Sei a eine positive Zahl und sei −a negativ. Dann und , wenn a=0 , dann .

Moduleigenschaften

Das Modul hat eine Reihe charakteristischer Ergebnisse - Moduleigenschaften. Jetzt geben wir die wichtigsten und am häufigsten verwendeten davon an. Zur Begründung dieser Eigenschaften stützen wir uns auf die Definition des Betrags einer Zahl über die Entfernung.

Beginnen wir mit der offensichtlichsten Moduleigenschaft − Modul einer Zahl kann keine negative Zahl sein. In wörtlicher Form hat diese Eigenschaft die Form für eine beliebige Zahl a . Diese Eigenschaft ist sehr einfach zu begründen: Der Betrag einer Zahl ist der Abstand, und der Abstand kann nicht als negative Zahl ausgedrückt werden.

Kommen wir zur nächsten Eigenschaft des Moduls. Der Modul einer Zahl ist genau dann gleich Null, wenn diese Zahl Null ist. Der Nullmodul ist per Definition Null. Null entspricht dem Ursprung, kein anderer Punkt auf der Koordinatenlinie entspricht Null, da jede reelle Zahl einem einzigen Punkt auf der Koordinatenlinie zugeordnet ist. Aus dem gleichen Grund entspricht jede andere Zahl als Null einem anderen Punkt als dem Ursprung. Und der Abstand vom Ursprung zu jedem anderen Punkt als dem Punkt O ist nicht gleich Null, da der Abstand zwischen zwei Punkten genau dann gleich Null ist, wenn diese Punkte zusammenfallen. Die obige Argumentation beweist, dass nur der Modul von Null gleich Null ist.

Weitergehen. Entgegengesetzte Zahlen haben gleiche Module, d. h. für jede Zahl a . Tatsächlich haben zwei Punkte auf der Koordinatenlinie, deren Koordinaten entgegengesetzte Zahlen sind, den gleichen Abstand vom Ursprung, was bedeutet, dass die Module entgegengesetzter Zahlen gleich sind.

Die nächste Moduleigenschaft ist: Der Modul des Produkts zweier Zahlen ist gleich dem Produkt der Module dieser Zahlen, also, . Per Definition ist der Betrag des Produkts der Zahlen a und b entweder a b if , oder −(a b) if . Aus den Regeln der Multiplikation reeller Zahlen folgt, dass das Produkt der Module der Zahlen a und b entweder gleich a b , , oder −(a b) ist, falls , was die betrachtete Eigenschaft beweist.

Der Modul des Quotienten der Division von a durch b ist gleich dem Quotienten der Division des Moduls von a durch den Modul von b, also, . Lassen Sie uns diese Eigenschaft des Moduls begründen. Da der Quotient gleich dem Produkt ist, gilt . Aufgrund der vorherigen Eigenschaft haben wir . Es bleibt nur noch die Gleichheit zu verwenden, die aufgrund der Definition des Betrags der Zahl gilt.

Die folgende Moduleigenschaft wird als Ungleichung geschrieben: , a , b und c sind beliebige reelle Zahlen. Die geschriebene Ungleichheit ist nichts anderes als Dreiecksungleichung. Um dies zu verdeutlichen, nehmen wir die Punkte A(a) , B(b) , C(c) auf der Koordinatenlinie und betrachten das entartete Dreieck ABC, dessen Eckpunkte auf derselben Linie liegen. Per Definition ist der Betrag der Differenz gleich der Länge des Segments AB, - der Länge des Segments AC und - der Länge des Segments CB. Da die Länge einer Seite eines Dreiecks die Summe der Längen der beiden anderen Seiten nicht überschreitet, ist die Ungleichung , also gilt auch die Ungleichung.

Die soeben bewiesene Ungleichung ist viel häufiger in der Form . Die geschriebene Ungleichung wird üblicherweise als eigenständige Eigenschaft des Moduls betrachtet mit der Formulierung: „ Der Betrag der Summe zweier Zahlen übersteigt nicht die Summe der Beträge dieser Zahlen". Aber die Ungleichung folgt direkt aus der Ungleichung , wenn wir −b anstelle von b einsetzen und c=0 nehmen.

Komplexer Zahlenmodul

Geben wir Bestimmung des Moduls einer komplexen Zahl. Lassen Sie sich geben komplexe Zahl, geschrieben in algebraischer Form , wobei x und y einige reelle Zahlen sind, die jeweils den reellen und imaginären Teil einer gegebenen komplexen Zahl z darstellen, und eine imaginäre Einheit ist.

Definition.

Der Modul einer komplexen Zahl z=x+i y heißt die arithmetische Quadratwurzel der Summe der Quadrate der Real- und Imaginärteile einer gegebenen komplexen Zahl.

Der Modul einer komplexen Zahl z wird als bezeichnet, dann kann die klingende Definition des Moduls einer komplexen Zahl geschrieben werden als .

Mit dieser Definition können Sie den Modul jeder komplexen Zahl in algebraischer Notation berechnen. Lassen Sie uns zum Beispiel den Modul einer komplexen Zahl berechnen. In diesem Beispiel ist der Realteil der komplexen Zahl , und der Imaginärteil minus vier. Dann haben wir nach der Definition des Moduls einer komplexen Zahl .

Die geometrische Interpretation des Moduls einer komplexen Zahl kann analog zur geometrischen Interpretation des Moduls einer reellen Zahl in Bezug auf die Entfernung angegeben werden.

Definition.

Komplexer Zahlenmodul z ist der Abstand vom Anfang der komplexen Ebene bis zu dem Punkt, der der Zahl z in dieser Ebene entspricht.

Nach dem Satz des Pythagoras wird die Entfernung vom Punkt O zum Punkt mit den Koordinaten (x, y) als gefunden, also , wobei . Daher stimmt die letzte Definition des Moduls einer komplexen Zahl mit der ersten überein.

Mit dieser Definition können Sie auch sofort angeben, was der Modul einer komplexen Zahl z ist, wenn sie in trigonometrischer Form geschrieben wird als oder in Exponentialform. Hier . Zum Beispiel der Modul einer komplexen Zahl ist 5 und der Modul der komplexen Zahl ist .

Es ist auch ersichtlich, dass das Produkt einer komplexen Zahl und ihrer komplexen Konjugierten die Summe der Quadrate des Real- und Imaginärteils ergibt. Wirklich, . Die resultierende Gleichheit erlaubt uns, eine weitere Definition des Moduls einer komplexen Zahl zu geben.

Definition.

Komplexer Zahlenmodul z ist die arithmetische Quadratwurzel des Produkts dieser Zahl und ihrer komplexen Konjugierten, also .

Abschließend halten wir fest, dass alle im entsprechenden Unterkapitel formulierten Eigenschaften des Moduls auch für komplexe Zahlen gelten.

Referenzliste.

Wilenkin N.Ja. usw. Mathematik. Klasse 6: Lehrbuch für Bildungseinrichtungen.
Makarychev Yu.N., Mindyuk N.G., Neshkov K.I., Suvorova S.B. Algebra: Lehrbuch für 8 Zellen. Bildungsinstitutionen.
Lunts G.L., Elsgolts L.E. Funktionen einer komplexen Variablen: ein Lehrbuch für Universitäten.
Priwalow I. I. Einführung in die Theorie der Funktionen einer komplexen Variablen.

Wir wissen bereits, dass die Menge der reellen Zahlen $R$ aus rationalen und irrationalen Zahlen besteht.

Rationale Zahlen können immer als Dezimalzahlen (endlich oder unendlich periodisch) dargestellt werden.

Irrationale Zahlen werden als unendliche, aber nicht wiederkehrende Dezimalzahlen geschrieben.

Die Menge der reellen Zahlen $R$ enthält auch die Elemente $-\infty $ und $+\infty $, für die die Ungleichungen $-\infty

Überlegen Sie, wie Sie reelle Zahlen darstellen können.

Gemeinsame Brüche

Definition

Ein Bruch heißt echt, wenn sein Zähler kleiner als sein Nenner ist. Umgekehrt heißt ein Bruch unecht, wenn sein Zähler größer oder gleich seinem Nenner ist.

Für gewöhnliche Brüche gibt es einfache, praktisch naheliegende Vergleichsregeln ($m$,$n$,$p$ sind natürliche Zahlen):

von zwei Brüchen mit gleichem Nenner ist der mit dem größeren Zähler größer, also $\frac(m)(p) >\frac(n)(p) $ für $m>n$;
von zwei Brüchen mit gleichem Zähler ist der mit dem kleineren Nenner größer, also $\frac(p)(m) >\frac(p)(n) $ für $ m
ein echter Bruch ist immer kleiner als eins; unechter Bruch ist immer größer als eins; ein Bruch, dessen Zähler gleich dem Nenner ist, ist gleich eins;
Jeder unechte Bruch ist größer als jeder echte Bruch.

Dezimal Zahlen

Definition

Beispiel 1

Wir ermitteln den Wert der Dezimalzahl 3,74. Wir erhalten: $3,74=3+\frac(7)(10) +\frac(4)(100) $.

Die Dezimalzahl kann gerundet werden. In diesem Fall müssen Sie die Stelle angeben, auf die gerundet wird.

Die Rundungsregel lautet wie folgt:

alle Ziffern rechts von dieser Ziffer werden durch Nullen ersetzt (wenn diese Ziffern vor dem Komma stehen) oder verworfen (wenn diese Ziffern nach dem Komma stehen);
Wenn die erste Ziffer nach der angegebenen Ziffer kleiner als 5 ist, wird die Ziffer dieser Ziffer nicht geändert.
Wenn die erste Ziffer nach der angegebenen Ziffer 5 oder mehr ist, wird die Ziffer dieser Ziffer um eins erhöht.

Beispiel 2

Runden wir die Zahl 17302 auf das nächste Tausend: 17000.
Runden wir die Zahl 17378 auf die nächsten Hunderter: 17400.
Runden wir die Zahl 17378,45 auf Zehner: 17380.
Runden wir die Zahl 378,91434 auf das nächste Hundertstel: 378,91.
Runden wir die Zahl 378,91534 auf das nächste Hundertstel: 378,92.

Umwandlung einer Dezimalzahl in einen gewöhnlichen Bruch.

Fall 1

Eine Dezimalzahl ist eine abschließende Dezimalzahl.

Die Konvertierungsmethode wird im folgenden Beispiel gezeigt.

Beispiel 2

Wir haben: $3,74=3+\frac(7)(10) +\frac(4)(100) $.

Reduzieren Sie auf einen gemeinsamen Nenner und erhalten Sie:

Der Bruch kann gekürzt werden: $3,74=\frac(374)(100) =\frac(187)(50) $.

Fall 2

Eine Dezimalzahl ist eine unendlich wiederkehrende Dezimalzahl.

Das Transformationsverfahren beruht darauf, dass der periodische Teil eines periodischen Dezimalbruchs als Summe der Glieder einer unendlich fallenden geometrischen Folge betrachtet werden kann.

Beispiel 4

$0,\left(74\right)=\frac(74)(100) +\frac(74)(10000) +\frac(74)(1000000) +\ldots $. Das erste Glied der Progression ist $a=0.74$, der Nenner der Progression ist $q=0.01$.

Beispiel 5

$0.5\left(8\right)=\frac(5)(10) +\frac(8)(100) +\frac(8)(1000) +\frac(8)(10000) +\ldots $ . Das erste Glied der Progression ist $a=0.08$, der Nenner der Progression ist $q=0.1$.

Die Summe der Glieder einer unendlich fallenden geometrischen Folge wird durch die Formel $s=\frac(a)(1-q) $ berechnet, wobei $a$ das erste Glied und $q$ der Nenner der Folge $ ist \links (0

Beispiel 6

Konvertieren wir den unendlichen periodischen Dezimalbruch $0,\left(72\right)$ in einen regulären.

Beispiel 7

Lassen Sie uns den unendlichen periodischen Dezimalbruch $0.5\left(3\right)$ in einen regulären Bruch umwandeln.

Das erste Glied der Progression ist $a=0.03$, der Nenner der Progression ist $q=0.1$. Wir erhalten: $s=\frac(a)(1-q) =\frac(0.03)(1-0.1) =\frac(0.03)(0.9) =\frac(3)( 90) =\frac(1). )(30)$.

Also $0,5\left(3\right)=\frac(5)(10) +\frac(1)(30) =\frac(5\cdot 3)(10\cdot 3) +\frac( 1)(30 ) =\frac(15)(30) +\frac(1)(30) =\frac(16)(30) =\frac(8)(15) $.

Reelle Zahlen lassen sich durch Punkte auf dem Zahlenstrahl darstellen.

Intervall $\left(a,\; b\right)$. Gleichzeitig $ a
Segment $\left$. Außerdem $a\le x\le b$.
Halbsegmente oder Halbintervalle $\left$. Gleichzeitig $ a \le x
Unendliche Spannen, zB $a

Der absolute Wert der Zahl

Geometrisch bedeutet $\left|x\right|$ den Abstand zwischen den Punkten $x$ und 0 auf der reellen Achse.

Eigenschaften von Absolutwerten:

aus der Definition folgt, dass $\left|x\right|\ge 0$, $\left|x\right|=\left|-x\right|$;
für den Betrag der Summe und für den Betrag der Differenz zweier Zahlen die Ungleichungen $\left|x+y\right|\le \left|x\right|+\left|y\right|$, $\ left|x-y\right|\le \left|x\right|+\left|y\right|$ und auch $\left|x+y\right|\ge \left|x\right|-\left|y \right|$,$\ left|x-y\right|\ge \left|x\right|-\left|y\right|$;
der Betrag des Produkts und der Betrag des Quotienten zweier Zahlen erfüllen die Gleichungen $\left|x\cdot y\right|=\left|x\right|\cdot \left|y\right|$ und $\left |\frac(x)( y) \right|=\frac(\left|x\right|)(\left|y\right|) $.

Ausgehend von der Definition des Betrages für eine beliebige Zahl $a>0$ kann man auch die Äquivalenz folgender Ungleichungspaare feststellen:

wenn $ \links|x\rechts|
if $\left|x\right|\le a$ then $-a\le x\le a$;
wenn $\left|x\right|>a$ dann entweder $xa$;
wenn $\left|x\right|\ge a$, dann entweder $x\le -a$ oder $x\ge a$.

Beispiel 8

Lösen Sie die Ungleichung $\left|2\cdot x+1\right|

Diese Ungleichung entspricht den Ungleichungen $-7

Von hier erhalten wir: $-8