Równanie parametryczne prostej na płaszczyźnie. Równania parametryczne Równanie prostej w postaci parametrycznej w przestrzeni

Koniecznie przeczytaj ten akapit! Oczywiście równania parametryczne nie są alfą i omegą geometrii przestrzennej, ale działającą mrówką wielu problemów. Co więcej, tego typu równania są często stosowane nieoczekiwanie i powiedziałbym elegancko.

Jeżeli znany jest punkt należący do prostej i wektor kierunkowy tej prostej, to równania parametryczne tej prostej są podane przez układ:

O samej koncepcji równań parametrycznych mówiłem na lekcjach Równanie prostej na płaszczyźnie oraz Pochodna funkcji zdefiniowanej parametrycznie.

Wszystko jest prostsze niż parzona rzepa, więc musisz urozmaicić zadanie:

Przykład 7

Decyzja: Linie są podane równaniami kanonicznymi iw pierwszym etapie należy znaleźć jakiś punkt należący do prostej i jej wektor kierunkowy.

a) Usuń punkt i wektor kierunkowy z równań: . Możesz wybrać inny punkt (jak to zrobić opisano powyżej), ale lepiej wybrać najbardziej oczywisty. Nawiasem mówiąc, aby uniknąć błędów, zawsze podmieniaj jego współrzędne w równaniach.

Skomponujmy równania parametryczne tej prostej:

Wygoda równań parametrycznych polega na tym, że za ich pomocą bardzo łatwo jest znaleźć inne punkty prostej. Na przykład znajdźmy punkt, którego współrzędne odpowiadają, powiedzmy, wartości parametru :

Zatem:

b) Rozważ równania kanoniczne . Wybór punktu jest tutaj prosty, ale podstępny: (uważaj, aby nie pomylić współrzędnych!!!). Jak wyciągnąć wektor prowadzący? Możesz spekulować, do czego ta linia jest równoległa, lub możesz użyć prostej formalnej sztuczki: proporcja to „y” i „Z”, więc zapisujemy wektor kierunku i wstawiamy zero w pozostałej przestrzeni: .

Układamy równania parametryczne prostej:

c) Przepiszmy równania w postaci , czyli „Z” może być dowolna. A jeśli tak, to niech na przykład . Zatem punkt należy do tej linii. Aby znaleźć wektor kierunkowy, posługujemy się następującą techniką formalną: w początkowych równaniach są „x” i „y”, a w wektorze kierunkowym w tych miejscach piszemy zera: . W pozostałe miejsce stawiamy jednostka: . Zamiast jedynki zrobi to dowolna liczba z wyjątkiem zera.

Piszemy równania parametryczne prostej:

Na trening:

Przykład 8

Napisz równania parametryczne dla następujących linii:

Rozwiązania i odpowiedzi na koniec lekcji. Twoje odpowiedzi mogą nieznacznie różnić się od moich, faktem jest, że równania parametryczne można zapisać na więcej niż jeden sposób. Ważne jest, aby twój i mój wektor kierunkowy były współliniowe i aby twój punkt "pasował" do moich równań (lub odwrotnie, mój punkt do twoich równań).

Jak inaczej można zdefiniować linię prostą w przestrzeni? Chciałbym wymyślić coś z wektorem normalnym. Jednak liczba nie zadziała, w przypadku linii przestrzennej wektory normalne mogą wyglądać w zupełnie innych kierunkach.

Inna metoda została już wspomniana w lekcji Równanie płaszczyzny i na początku tego artykułu.

KĄT MIĘDZY PŁASZCZAMI

Rozważmy dwie płaszczyzny α 1 i α 2 podane odpowiednio przez równania:

Pod narożnik między dwiema płaszczyznami mamy na myśli jeden z dwuściennych kątów utworzonych przez te płaszczyzny. Jest oczywiste, że kąt między wektorami normalnymi a płaszczyznami α 1 i α 2 jest równy jednemu ze wskazanych sąsiednich kątów dwuściennych lub . Więc . Ponieważ oraz , następnie

Przykład. Określ kąt między płaszczyznami x+2tak-3z+4=0 i 2 x+3tak+z+8=0.

Warunek równoległości dwóch płaszczyzn.

Dwie płaszczyzny α 1 i α 2 są równoległe wtedy i tylko wtedy, gdy ich wektory normalne i są równoległe, a zatem .

Tak więc dwie płaszczyzny są równoległe do siebie wtedy i tylko wtedy, gdy współczynniki w odpowiednich współrzędnych są proporcjonalne:

lub

Warunek prostopadłości płaszczyzn.

Jasne jest, że dwie płaszczyzny są prostopadłe wtedy i tylko wtedy, gdy ich wektory normalne są prostopadłe, a zatem lub .

Zatem, .

Przykłady.

BEZPOŚREDNIO W KOSMOSIE.

RÓWNANIE WEKTOROWE BEZPOŚREDNIE.

RÓWNANIA PARAMETRYCZNE DIRECT

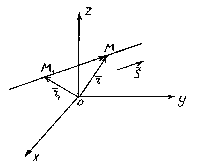
Położenie linii prostej w przestrzeni jest całkowicie określane przez określenie dowolnego z jej punktów stałych M 1 i wektor równoległy do tej linii.

Wektor równoległy do linii prostej nazywa się prowadzenie wektor tej linii.

Więc niech prosta ja przechodzi przez punkt M 1 (x 1 , tak 1 , z 1) leżące na linii prostej równoległej do wektora .

Rozważ dowolny punkt M(x,y,z) na linii prostej. Na rysunku widać, że .

Wektory i są współliniowe, więc jest taka liczba t, co , gdzie jest mnożnik t może przyjmować dowolną wartość liczbową w zależności od położenia punktu M na linii prostej. Czynnik t nazywa się parametrem. Oznaczanie promieniowych wektorów punktów M 1 i M odpowiednio przez i otrzymujemy . To równanie nazywa się wektor równanie linii prostej. Pokazuje, że każda wartość parametru t odpowiada wektorowi promienia pewnego punktu M leżąc na linii prostej.

Piszemy to równanie w postaci współrzędnych. Zauważ, że , i stąd

Powstałe równania nazywają się parametryczny równania linii prostych.

Podczas zmiany parametru t zmiana współrzędnych x, tak oraz z i kropka M porusza się w linii prostej.

RÓWNANIA KANONICZNE BEZPOŚREDNIE

Zostawiać M 1 (x 1 , tak 1 , z 1) - punkt leżący na linii prostej ja, oraz jest jego wektorem kierunkowym. Ponownie weź dowolny punkt na linii prostej M(x,y,z) i rozważmy wektor .

Jasne jest, że wektory i są współliniowe, więc ich współrzędne muszą być proporcjonalne, stąd

– kanoniczny równania linii prostych.

Uwaga 1. Zauważ, że równania kanoniczne prostej można uzyskać z równań parametrycznych, eliminując parametr t. Rzeczywiście, z równań parametrycznych, które otrzymujemy lub .

Przykład. Napisz równanie linii prostej w sposób parametryczny.

Oznaczać , W związku z tym x = 2 + 3t, tak = –1 + 2t, z = 1 –t.

Uwaga 2. Niech linia będzie prostopadła do jednej z osi współrzędnych, na przykład oś Wół. Wtedy wektor kierunkowy prostej jest prostopadły Wół, W związku z tym, m=0. W konsekwencji równania parametryczne prostej przyjmują postać

Eliminacja parametru z równań t otrzymujemy równania prostej w postaci

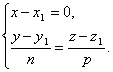
Jednak i w tym przypadku zgadzamy się formalnie zapisać równania kanoniczne prostej w postaci . Tak więc, jeśli mianownik jednej z ułamków wynosi zero, oznacza to, że linia jest prostopadła do odpowiedniej osi współrzędnych.

Podobnie, równania kanoniczne odpowiada linii prostej prostopadłej do osi Wół oraz Oy lub oś równoległa Oz.

Przykłady.

RÓWNANIA OGÓLNE LINIA PROSTA JAKO LINIA PRZECIĘCIA DWÓCH PŁASZCZYZN

Przez każdą prostą w przestrzeni przechodzi nieskończona liczba płaszczyzn. Dowolne dwa z nich, przecinające się, definiują go w przestrzeni. Dlatego równania dowolnych dwóch takich płaszczyzn, rozpatrywane razem, są równaniami tej linii.

Ogólnie rzecz biorąc, dowolne dwie nierównoległe płaszczyzny podane przez równania ogólne

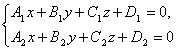
określić ich linię przecięcia. Te równania nazywają się równania ogólne prosty.

Przykłady.

Skonstruuj linię prostą podaną przez równania

Aby skonstruować prostą wystarczy znaleźć dowolne dwa jej punkty. Najłatwiej jest wybrać punkty przecięcia linii z płaszczyznami współrzędnych. Na przykład punkt przecięcia z płaszczyzną xOy otrzymujemy z równań prostej, zakładając: z= 0:

Rozwiązując ten system, znajdujemy punkt M 1 (1;2;0).

Podobnie, zakładając tak= 0, otrzymujemy punkt przecięcia prostej z płaszczyzną xOz:

Z ogólnych równań prostej można przejść do jej równań kanonicznych lub parametrycznych. Aby to zrobić, musisz znaleźć jakiś punkt M 1 na linii i wektor kierunkowy linii.

Współrzędne punktu M 1 otrzymujemy z tego układu równań, nadając jednej ze współrzędnych dowolną wartość. Aby znaleźć wektor kierunku, zauważ, że ten wektor musi być prostopadły do obu wektorów normalnych oraz . Dlatego dla wektora kierunkowego prostej ja możesz wziąć iloczyn krzyżowy wektorów normalnych:

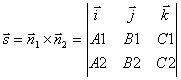Przykład. Podaj ogólne równania linii prostej do formy kanonicznej.

Znajdź punkt na linii prostej. W tym celu wybieramy dowolnie jedną ze współrzędnych, np. tak= 0 i rozwiąż układ równań:

Wektory normalne płaszczyzn definiujących linię mają współrzędne Dlatego wektor kierunku będzie prosty

. Stąd, ja: .

KĄT MIĘDZY PRAWAMI

narożnik pomiędzy liniami prostymi w przestrzeni nazwiemy dowolny z sąsiednich kątów utworzonych przez dwie proste linie poprowadzone przez dowolny punkt równoległy do danych.

Niech dwie linie proste zostaną podane w przestrzeni:

Oczywiście kąt φ między liniami można przyjąć jako kąt między ich wektorami kierunkowymi i . Ponieważ , to zgodnie ze wzorem na cosinus kąta między wektorami otrzymujemy

Jednym z podpunktów tematu „Równanie prostej na płaszczyźnie” jest zagadnienie zestawienia równań parametrycznych prostej na płaszczyźnie w prostokątnym układzie współrzędnych. W poniższym artykule omówiono zasadę kompilacji takich równań dla pewnych znanych danych. Pokażmy, jak przejść od równań parametrycznych do równań o innej postaci; Przeanalizujmy rozwiązanie typowych problemów.

Konkretną linię można zdefiniować, określając punkt należący do tej linii i wektor kierunku dla linii.

Załóżmy, że mamy prostokątny układ współrzędnych O x y . A także podana jest prosta a, wskazująca leżący na niej punkt M 1 (x 1, y 1) oraz wektor kierunkowy danej prostej a → = (a x , a y) . Podajemy opis danej linii za pomocą równań.

Używamy dowolnego punktu M (x, y) i otrzymujemy wektor M 1 M →; obliczyć jego współrzędne ze współrzędnych punktu początkowego i końcowego: M 1 M → = (x - x 1 , y - y 1 ). Opiszmy wynik: prosta jest wyznaczona przez zbiór punktów M (x, y), przechodzi przez punkt M 1 (x 1, y 1) i ma wektor kierunkowy a → = (a x , a y) . Podany zbiór definiuje linię prostą tylko wtedy, gdy wektory M 1 M → = (x - x 1 , y - y 1) i a → = (a x , a y) są współliniowe.

Istnieje warunek konieczny i wystarczający na kolinearność wektorów, który w tym przypadku dla wektorów M 1 M → = (x - x 1 , y - y 1) oraz a → = (a x , a y) można zapisać jako równanie:

M 1 M → = λ · a → , gdzie λ jest pewną liczbą rzeczywistą.

Definicja 1

Równanie M 1 M → = λ · a → nazywa się wektorowo-parametrycznym równaniem prostej.

W postaci współrzędnych wygląda to tak:

M 1 M → = λ a → ⇔ x - x 1 = λ a x y - y 1 = λ a y ⇔ x = x 1 + a x λ y = y 1 + a y λ

Równania wynikowego układu x = x 1 + a x · λ y = y 1 + a y · λ nazywane są równaniami parametrycznymi prostej na płaszczyźnie w prostokątnym układzie współrzędnych. Istota nazwy jest następująca: współrzędne wszystkich punktów prostej można wyznaczyć za pomocą równań parametrycznych na płaszczyźnie postaci x = x 1 + a x λ y = y 1 + a y λ przy iteracji po wszystkich wartościach rzeczywistych parametru λ

Zgodnie z powyższym równania parametryczne linii prostej na płaszczyźnie x \u003d x 1 + a x λ y \u003d y 1 + a y λ określają linię prostą podaną w prostokątnym układzie współrzędnych, przechodzącą przez punkt M 1 (x 1, y 1) i ma wektor przewodni a → = (a x , a y) . Jeśli więc podano współrzędne pewnego punktu prostej i współrzędne jego wektora kierunkowego, to można od razu zapisać równania parametryczne danej prostej.

Przykład 1

Konieczne jest ułożenie równań parametrycznych prostej na płaszczyźnie w układzie współrzędnych prostokątnych, jeżeli podano należący do niej punkt M 1 (2, 3) i jego wektor kierunkowy a → = (3 , 1) .

Decyzja

Na podstawie danych początkowych otrzymujemy: x 1 \u003d 2, y 1 \u003d 3, a x \u003d 3, a y \u003d 1. Równania parametryczne będą wyglądać następująco:

x = x 1 + a x λ y = y 1 + a y λ ⇔ x = 2 + 3 λ y = 3 + 1 λ ⇔ x = 2 + 3 λ y = 3 + λ

Zilustrujmy jasno:

Odpowiedź: x = 2 + 3 λ y = 3 + λ

Należy zauważyć: jeśli wektor a → = (a x , a y) służy jako wektor kierunkowy prostej a, a należą do niej punkty M 1 (x 1, y 1) i M 2 (x 2, y 2), to można go wyznaczyć za pomocą równań parametrycznych postaci : x = x 1 + a x λ y = y 1 + a y λ , a także ta opcja: x = x 2 + a x λ y = y 2 + a y λ .

Na przykład otrzymujemy wektor kierujący linii prostej a → \u003d (2, - 1), a także punkty M 1 (1, - 2) i M 2 (3, - 3) należące do tej linii. Następnie linię prostą wyznacza się za pomocą równań parametrycznych: x = 1 + 2 · λ y = - 2 - λ lub x = 3 + 2 · λ y = - 3 - λ .

Należy również zwrócić uwagę na następujący fakt: jeśli a → = (a x , a y) jest wektorem kierunkowym prostej a , to każdy z wektorów będzie również jej wektorem kierunkowym μ a → = (μ a x , μ a y) , gdzie μ ϵ R , μ ≠ 0 .

Zatem linię prostą a na płaszczyźnie w prostokątnym układzie współrzędnych można zdefiniować równaniami parametrycznymi: x = x 1 + μ a x λ y = y 1 + μ a y λ dla dowolnej wartości μ różnej od zera.

Załóżmy, że linia a jest określona równaniami parametrycznymi x = 3 + 2 λ y = - 2 - 5 λ . Następnie a → = (2 , - 5) - wektor kierunkowy tej linii. A także każdy z wektorów μ · a → = (μ · 2 , μ · - 5) = 2 μ , - 5 μ , μ ∈ R , μ ≠ 0 stanie się wektorem kierunkowym dla danej linii prostej. Dla jasności rozważmy konkretny wektor - 2 · a → = (- 4 , 10) , odpowiada on wartości μ = - 2 . W tym przypadku daną linię prostą można również wyznaczyć za pomocą równań parametrycznych x = 3 - 4 · λ y = - 2 + 10 · λ .

Przejście od równań parametrycznych prostej na płaszczyźnie do innych równań danej prostej i odwrotnie

W rozwiązywaniu niektórych problemów zastosowanie równań parametrycznych nie jest opcją najbardziej optymalną, wówczas konieczne staje się przełożenie równań parametrycznych prostej na równania prostej innego typu. Zobaczmy, jak to zrobić.

Równania parametryczne prostej x = x 1 + a x · λ y = y 1 + a y · λ będą odpowiadały równaniu kanonicznemu prostej na płaszczyźnie x - x 1 a x = y - y 1 a y .

Rozwiązujemy każde z równań parametrycznych względem parametru λ, przyrównujemy prawe części otrzymanych równości i otrzymujemy równanie kanoniczne danej prostej:

x = x 1 + a x λ y = y 1 + a y λ ⇔ λ = x - x 1 a x λ = y - y 1 a y ⇔ x - x 1 a x = y - y 1 a y

W takim przypadku nie powinno być krępujące, jeśli x lub ay będą równe zero.

Przykład 2

Należy przeprowadzić przejście od równań parametrycznych prostej x = 3 y = - 2 - 4 · λ do równania kanonicznego.

Decyzja

Zapisane równania parametryczne zapisujemy w postaci: x = 3 + 0 λ y = - 2 - 4 λ

Parametr λ wyrażamy w każdym z równań: x = 3 + 0 λ y = - 2 - 4 λ ⇔ λ = x - 3 0 λ = y + 2 - 4

Przyrównujemy właściwe części układu równań i otrzymujemy wymagane równanie kanoniczne prostej w płaszczyźnie:

x - 3 0 = y + 2 - 4

Odpowiedź: x - 3 0 = y + 2 - 4

W przypadku, gdy konieczne jest spisanie równania prostej postaci A x + B y + C = 0 , a dane są równania parametryczne prostej na płaszczyźnie należy najpierw wykonać przejście do równania kanonicznego, a następnie do ogólnego równania prostej. Zapiszmy całą sekwencję działań:

x = x 1 + a x λ y = y 1 + a y λ ⇔ λ = x - x 1 a x λ = y - y 1 a y ⇔ x - x 1 a x = y - y 1 a y ⇔ ⇔ a y (x - x 1) = a x (y - y 1) ⇔ A x + B y + C = 0

Przykład 3

Należy spisać ogólne równanie prostej, jeśli podano równania parametryczne, które ją definiują: x = - 1 + 2 λ y = - 3 λ

Decyzja

Najpierw przejdźmy do równania kanonicznego:

x = - 1 + 2 λ y = - 3 λ ⇔ λ = x + 1 2 λ = y - 3 ⇔ x + 1 2 = y - 3

Wynikowa proporcja jest identyczna z równością - 3 · (x + 1) = 2 · y. Otwórzmy nawiasy i uzyskajmy ogólne równanie prostej: - 3 x + 1 = 2 y ⇔ 3 x + 2 y + 3 = 0 .

Odpowiedź: 3x + 2 lata + 3 = 0

Kierując się powyższą logiką działań, w celu uzyskania równania prostej ze spadkiem, równania prostej w odcinkach lub równania normalnego prostej, konieczne jest uzyskanie ogólnego równania prostej , a następnie przeprowadzić dalsze przejście.

Rozważmy teraz działanie odwrotne: zapisanie równań parametrycznych prostej dla innej podanej postaci równań tej prostej.

Najłatwiejsze przejście: od równania kanonicznego do parametrycznego. Niech zostanie podane równanie kanoniczne postaci: x - x 1 a x = y - y 1 a y . Przyjmujemy każdą z relacji tej równości równą parametrowi λ:

x - x 1 a x = y - y 1 a y = λ ⇔ λ = x - x 1 a x λ = y - y 1 a y

Rozwiążmy otrzymane równania dla zmiennych x i y:

x = x 1 + a x λ y = y 1 + a y λ

Przykład 4

Równania parametryczne prostej należy spisać, jeśli znane jest równanie kanoniczne prostej na płaszczyźnie: x - 2 5 = y - 2 2

Decyzja

Zrównajmy części znanego równania z parametrem λ: x - 2 5 = y - 2 2 = λ . Z otrzymanej równości otrzymujemy równania parametryczne prostej: x - 2 5 = y - 2 2 = λ ⇔ λ = x - 2 5 λ = y - 2 5 ⇔ x = 2 + 5 λ y = 2 + 2 λ

Odpowiedź: x = 2 + 5 λ y = 2 + 2 λ

Gdy konieczne jest przejście do równań parametrycznych z danego ogólnego równania prostej, równania prostej ze spadkiem lub równania prostej w odcinkach, konieczne jest doprowadzenie pierwotnego równania do kanoniczny, a następnie przejść do równań parametrycznych.

Przykład 5

Konieczne jest spisanie równań parametrycznych prostej ze znanym ogólnym równaniem tej prostej: 4 x - 3 y - 3 = 0 .

Decyzja

Przekształcamy podane równanie ogólne w równanie postaci kanonicznej:

4 x - 3 r - 3 = 0 ⇔ 4 x = 3 r + 3 ⇔ ⇔ 4 x = 3 r + 1 3 ⇔ x 3 = r + 1 3 4

Przyrównujemy obie części równości do parametru λ i otrzymujemy wymagane równania parametryczne prostej:

x 3 = y + 1 3 4 = λ ⇔ x 3 = λ y + 1 3 4 = λ ⇔ x = 3 λ y = - 1 3 + 4 λ

Odpowiedź: x = 3 λ y = - 1 3 + 4 λ

Przykłady i problemy z równaniami parametrycznymi prostej na płaszczyźnie

Rozważmy najczęstsze typy problemów, wykorzystując równania parametryczne prostej na płaszczyźnie w prostokątnym układzie współrzędnych.

W zadaniach pierwszego typu podaje się współrzędne punktów, niezależnie od tego, czy należą one do linii prostej opisanej równaniami parametrycznymi.

Rozwiązanie takich problemów opiera się na następującym fakcie: liczby (x, y) określone na podstawie równań parametrycznych x \u003d x 1 + a x λ y \u003d y 1 + a y λ dla pewnej wartości rzeczywistej λ są współrzędnymi a punkt należący do prostej, którą opisują te równania parametryczne.

Przykład 6

Niezbędne jest wyznaczenie współrzędnych punktu leżącego na linii prostej określonej równaniami parametrycznymi x = 2 - 1 6 · λ y = - 1 + 2 · λ dla λ = 3 .

Decyzja

Podstawiamy znaną wartość λ = 3 do podanych równań parametrycznych i obliczamy żądane współrzędne: x = 2 - 1 6 3 y = - 1 + 2 3 ⇔ x = 1 1 2 y = 5

Odpowiedź: 1 1 2 , 5

Możliwy jest również następujący problem: niech jakiś punkt M 0 (x 0, y 0) będzie podany na płaszczyźnie w prostokątnym układzie współrzędnych i należy określić, czy ten punkt należy do prostej opisanej równaniami parametrycznymi x = x 1 + a x λ y = y 1 + a y λ .

Aby rozwiązać taki problem, konieczne jest podstawienie współrzędnych danego punktu do znanych równań parametrycznych prostej. Jeżeli zostanie stwierdzone, że taka wartość parametru λ = λ 0 jest możliwa, w której oba równania parametryczne są prawdziwe, to dany punkt należy do danej prostej.

Przykład 7

Podano punkty M 0 (4, - 2) i N 0 (- 2, 1). Należy określić, czy należą one do linii prostej określonej równaniami parametrycznymi x = 2 · λ y = - 1 - 1 2 · λ .

Decyzja

Podstawiamy współrzędne punktu M 0 (4, - 2) do podanych równań parametrycznych:

4 = 2 λ - 2 = - 1 - 1 2 λ ⇔ λ = 2 λ = 2 ⇔ λ = 2

Wnioskujemy, że punkt M 0 należy do danej prostej, ponieważ odpowiada wartości λ = 2 .

2 = 2 λ 1 = - 1 - 1 2 λ ⇔ λ = - 1 λ = - 4

Jest oczywiste, że nie ma takiego parametru λ, któremu odpowiadałby punkt N 0. Innymi słowy, dana prosta nie przechodzi przez punkt N 0 (- 2 , 1 ).

Odpowiedź: punkt M 0 należy do danej linii; punkt N 0 nie należy do danej prostej.

W problemach drugiego typu wymagane jest układanie równań parametrycznych prostej na płaszczyźnie w prostokątnym układzie współrzędnych. Najprostszy przykład takiego problemu (ze znanymi współrzędnymi punktu prostej i wektorem kierunkowym) omówiono powyżej. Spójrzmy teraz na przykłady, w których najpierw musisz znaleźć współrzędne wektora kierunkowego, a następnie zapisać równania parametryczne.

Przykład 8

Podano punkt M 1 1 2 , 2 3 . Konieczne jest skomponowanie równań parametrycznych linii prostej przechodzącej przez ten punkt i równoległej linii prostej x 2 \u003d y - 3 - 1.

Decyzja

W zależności od stanu problemu linia prosta, której równanie musimy wyprzedzić, jest równoległa do linii prostej x 2 \u003d y - 3 - 1. Wówczas jako wektor kierunkowy prostej przechodzącej przez dany punkt można wykorzystać wektor kierunkowy prostej x 2 = y - 3 - 1, który zapisujemy w postaci: a → = (2, - 1) . Teraz znane są wszystkie niezbędne dane, aby skomponować pożądane równania parametryczne:

x = x 1 + a x λ y = y 1 + a y λ ⇔ x = 1 2 + 2 λ y = 2 3 + (- 1) λ ⇔ x = 1 2 + x λ y = 2 3 - λ

Odpowiedź: x = 1 2 + x λ y = 2 3 - λ .

Przykład 9

Podano punkt M 1 (0, - 7). Konieczne jest napisanie równań parametrycznych prostej przechodzącej przez ten punkt prostopadle do prostej 3 x – 2 y – 5 = 0 .

Decyzja

Jako wektor kierunkowy prostej, z której równanie musi się składać, można przyjąć wektor normalny prostej 3 x - 2 y - 5 = 0 . Jego współrzędne to (3 , - 2 ). Piszemy wymagane równania parametryczne prostej:

x = x 1 + a x λ y = y 1 + a y λ ⇔ x = 0 + 3 λ y = - 7 + (- 2) λ ⇔ x = 3 λ y = - 7 - 2 λ

Odpowiedź: x = 3 λ y = - 7 - 2 λ

W problemach trzeciego typu wymagane jest przejście od równań parametrycznych danej prostej do innych typów równań, które ją określają. Rozważaliśmy rozwiązanie takich przykładów powyżej, podamy jeszcze jeden.

Przykład 10

Dana linia prosta na płaszczyźnie w prostokątnym układzie współrzędnych, określona równaniami parametrycznymi x = 1 - 3 4 · λ y = - 1 + λ . Konieczne jest znalezienie współrzędnych jakiegoś wektora normalnego tej prostej.

Decyzja

Aby określić pożądane współrzędne wektora normalnego, dokonamy przejścia z równań parametrycznych do równania ogólnego:

x = 1 - 3 4 λ y = - 1 + λ ⇔ λ = x - 1 - 3 4 λ = y + 1 1 ⇔ x - 1 - 3 4 = y + 1 1 ⇔ ⇔ 1 x - 1 = - 3 4 y + 1 ⇔ x + 3 4 y - 1 4 = 0

Współczynniki zmiennych x i y dają nam wymagane współrzędne wektora normalnego. Zatem wektor normalny prostej x = 1 - 3 4 · λ y = - 1 + λ ma współrzędne 1 , 3 4 .

Odpowiedź: 1 , 3 4 .

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter

Równania parametryczne prostej otrzymuje się elementarnie z równania kanonicznego tej prostej, które ma postać . Jako parametr przyjmijmy wartość, przez którą można pomnożyć lewą i prawą część równania kanonicznego.

Ponieważ jeden z mianowników jest z konieczności różny od zera, a odpowiadający mu licznik może przyjmować dowolne wartości, zakres parametru to cała oś liczb rzeczywistych: .

Otrzymamy lub wreszcie

Równania (1) to pożądane równania parametryczne linii prostej. Te równania umożliwiają interpretację mechaniczną. Jeżeli przyjmiemy, że parametrem jest czas mierzony od pewnego momentu początkowego, to równania parametryczne określają prawo ruchu punktu materialnego po linii prostej ze stałą prędkością (ruch taki występuje na zasadzie bezwładności).

Przykład 1 Ułóż na płaszczyźnie równania parametryczne prostej przechodzącej przez punkt i mającej wektor kierunkowy.

Decyzja. Podstawiamy dane punktu i wektora kierunku w (1) i otrzymujemy:

Często w zadaniach wymagane jest przekształcenie równań parametrycznych prostej na inne typy równań, a z równań innych typów uzyskanie równań parametrycznych prostej. Spójrzmy na kilka takich przykładów. Aby przekształcić równania parametryczne linii prostej na ogólne równanie prostej najpierw należy je sprowadzić do postaci kanonicznej, a następnie z równania kanonicznego, aby otrzymać ogólne równanie prostej

Przykład 2 Napisz równanie linii prostej

ogólnie.

Decyzja. Najpierw wprowadzamy równania parametryczne prostej do równania kanonicznego:

Dalsze przekształcenia sprowadzają równanie do postaci ogólnej:

Nieco trudniej jest przekształcić równanie ogólne w równania parametryczne linii prostej, ale dla tego działania można również opracować przejrzysty algorytm. Najpierw możemy przekształcić równanie ogólne na równanie nachylenia i znajdź z niego współrzędne jakiegoś punktu należącego do prostej, nadając jednej ze współrzędnych dowolną wartość. Znając współrzędne punktu i wektor kierunkowy (z ogólnego równania), można zapisać równania parametryczne prostej.

Przykład 3 Napisz równanie prostej w postaci równań parametrycznych.

Decyzja. Wprowadzamy ogólne równanie prostej do równania o nachyleniu:

Znajdujemy współrzędne jakiegoś punktu należącego do prostej. Nadaj jednej ze współrzędnych punktu dowolną wartość

Z równania prostej ze spadkiem otrzymujemy kolejną współrzędną punktu:

W ten sposób znamy wektor punktu i kierunku . Podstawiamy ich dane do (1) i otrzymujemy żądane równania parametryczne prostej:

Przykład 4 Znajdź nachylenie prostej podanej przez równania parametryczne

Decyzja. Równania parametryczne prostej należy najpierw przekształcić w równanie kanoniczne, następnie w równanie ogólne, a na końcu w równanie nachylenia.

Zatem nachylenie danej linii prostej:

Przykład 5 Ułóż równania parametryczne linii prostej przechodzącej przez punkt i linię prostopadłą

Przyrównanie w równaniach kanonicznych prostej każdej z ułamków do jakiegoś parametru t:

Otrzymujemy równania wyrażające aktualne współrzędne każdego punktu prostej poprzez parametr t.

zatem równania parametryczne prostej mają postać:

Równania prostej przechodzącej przez dwa zadane punkty.

Niech dwa punkty M 1 (x1,y1,z1) i M 2 (x2,y2,z2). Równania prostej przechodzącej przez dwa dane punkty otrzymuje się w taki sam sposób, jak podobne równanie na płaszczyźnie. Dlatego od razu podajemy formę tego równania.

Linia prosta na przecięciu dwóch płaszczyzn. Ogólne równanie prostej w przestrzeni.

Jeśli weźmiemy pod uwagę dwie nierównoległe płaszczyzny, to ich przecięcie będzie linią prostą.

Jeśli wektory normalne i niewspółliniowe.

Poniżej, rozważając przykłady, pokażemy sposób przekształcenia takich równań prostych w równania kanoniczne.

5.4 Kąt między dwiema liniami prostymi. Warunek równoległości i prostopadłości dwóch prostych.

Kąt między dwiema liniami prostymi w przestrzeni to dowolny z kątów utworzonych przez dwie linie proste poprowadzone przez dowolny punkt równoległy do danych.

Niech dwie linie będą podane przez ich równania kanoniczne.

Jako kąt między dwiema liniami prostymi przyjmiemy kąt między wektorami kierunku.

oraz

Warunek prostopadłości dwóch prostych sprowadza się do warunku prostopadłości ich wektorów kierunkowych i , czyli do równości do zera iloczynu skalarnego: lub w postaci współrzędnych: .

Warunek równoległości dwóch prostych sprowadza się do warunku równoległości ich wektorów kierunkowych i

5.5 Wzajemne ułożenie linii prostej i płaszczyzny.

Niech będą podane równania prostej:

i samoloty. Kąt między linią a płaszczyzną będzie dowolnym z dwóch sąsiednich kątów utworzonych przez linię i jej rzut na płaszczyznę (rysunek 5.5).

Rysunek 5.5

Jeśli linia jest prostopadła do płaszczyzny, wektor kierunkowy linii i wektor normalny do płaszczyzny są współliniowe. Zatem warunek prostopadłości linii prostej i płaszczyzny sprowadza się do warunku wektorów współliniowych

W przypadku równoległości prostej i płaszczyzny ich wektory wskazane powyżej są wzajemnie prostopadłe. Dlatego warunek równoległości prostej i płaszczyzny sprowadza się do warunku prostopadłości wektorów; tych. ich iloczyn skalarny wynosi zero lub w postaci współrzędnych: .

Poniżej przykłady rozwiązywania problemów związanych z tematem Rozdziału 5.

Przykład 1:

Napisz równanie dla płaszczyzny przechodzącej przez punkt A (1,2,4) prostopadle do prostej podanej równaniem:

Decyzja:

Korzystamy z równania płaszczyzny przechodzącej przez dany punkt prostopadle do danego wektora.

A(x-x 0)+B(y-y 0)+C(z-z 0)=0

Jako punkt przyjmujemy punkt A (1,2,4), przez który samolot przechodzi przez warunek.

Znając równania kanoniczne prostej, znamy wektor równoległy do prostej.

Ze względu na to, że pod warunkiem, że linia jest prostopadła do pożądanej płaszczyzny, wektor kierunku można przyjąć jako wektor normalny płaszczyzny.

W ten sposób otrzymujemy równanie płaszczyzny w postaci:

2(x-1)+1(y-2)+4(z-4)=0

2x+y+4z-16=0

2x+y+4z-20=0

Przykład 2:

Znajdź w samolocie 4x-7y+5z-20=0 punkt P, dla którego OP tworzy równe kąty z osiami współrzędnych.

Decyzja:

Zróbmy schematyczny rysunek. (Rysunek 5.6)

Rysunek 5.6

Pusty punkt Р ma współrzędne. Ponieważ wektor tworzy te same kąty z osiami współrzędnych, cosinusy kierunku tego wektora są sobie równe

Znajdźmy rzuty wektora:

wtedy można łatwo znaleźć cosinusy kierunku tego wektora.

Z równości cosinusów kierunku wynika równość:

x p \u003d y p \u003d z p

ponieważ punkt P leży na płaszczyźnie, zastąpienie współrzędnych tego punktu równaniem płaszczyzny zamienia go w tożsamość.

4x p -7x p +5x p -20=0

2x p \u003d 20

x p \u003d 10

Odpowiednio: y r=10; z p=10.

Zatem żądany punkt P ma współrzędne P (10; 10; 10)

Przykład 3:

Biorąc pod uwagę dwa punkty A (2, -1, -2) i B (8, -7,5). Znajdź równanie płaszczyzny przechodzącej przez punkt B, prostopadłej do odcinka AB.

Decyzja:

Aby rozwiązać problem, użyjemy równania płaszczyzny przechodzącej przez dany punkt prostopadle do danego wektora.

A(x-x 0)+B(y-y 0)+C(z-z 0)=0

Jako punkt używamy punktu B (8, -7,5), a jako wektora prostopadłego do płaszczyzny wektora. Znajdźmy rzuty wektora:

wtedy otrzymujemy równanie płaszczyzny w postaci:

6(x-8)-6(y+7)+7(z-5)=0

6x-48-6y-42+7z-35=0

6x-6y+7z-35=0

6x-6y+7z-125=0

Przykład 4:

Znajdź równanie płaszczyzny równoległej do osi OY i przechodzącej przez punkty K(1,-5,1) i M(3,2,-2).

Decyzja:

Ponieważ płaszczyzna jest równoległa do osi OY, użyjemy niepełnego równania płaszczyzny.

Topór+Cz+D=0

Ze względu na to, że punkty K i M leżą na płaszczyźnie, otrzymujemy dwa warunki.

Wyraźmy z tych warunków współczynniki A i C w postaci D.

Znalezione współczynniki podstawiamy do niepełnego równania płaszczyzny:

ponieważ , wtedy zmniejszamy D:

Przykład 5:

Znajdź równanie płaszczyzny przechodzącej przez trzy punkty M(7,6,7), K(5,10,5), R(-1,8,9)

Decyzja:

Wykorzystajmy równanie płaszczyzny przechodzącej przez 3 podane punkty.

podstawiając współrzędne punktów M, K, R jako pierwszy, drugi i trzeci otrzymujemy:

rozwiń wyznacznik wzdłuż pierwszej linii.

Przykład 6:

Znajdź równanie płaszczyzny przechodzącej przez punkty M 1 (8, -3,1); M 2 (4,7,2) i prostopadłe do płaszczyzny 3x+5y-7z-21=0

Decyzja:

Zróbmy schematyczny rysunek (rysunek 5.7)

Rysunek 5.7

Oznaczamy daną płaszczyznę P 2 i pożądaną płaszczyznę P 2. . Z równania danej płaszczyzny Р 1 wyznaczamy rzuty wektora prostopadłego do płaszczyzny Р 1.

Wektor można przesunąć do płaszczyzny P 2 za pomocą przesunięcia równoległego, ponieważ zgodnie z warunkiem zadania płaszczyzna P 2 jest prostopadła do płaszczyzny P 1, co oznacza, że wektor jest równoległy do płaszczyzny P 2.

Znajdźmy rzuty wektora leżącego na płaszczyźnie Р 2:

teraz mamy dwa wektory leżące w płaszczyźnie R 2 . Oczywiście wektor równy iloczynowi wektorowemu wektorów i będzie prostopadły do płaszczyzny P 2, ponieważ jest prostopadły, a zatem jego wektor normalny do płaszczyzny P 2.

Wektory i są podane przez ich rzuty, dlatego:

Następnie korzystamy z równania płaszczyzny przechodzącej przez dany punkt prostopadły do wektora. Jako punkt możesz wziąć dowolny z punktów M 1 lub M 2, na przykład M 1 (8, -3.1); Jako wektor normalny do płaszczyzny Р 2 przyjmujemy .

74(x-8)+25(y+3)+50(z-1)=0

3(x-8)+(y-3)+2(z-1)=0

3x-24+y+3+27-2=0

3x+y+2z-23=0

Przykład 7:

Linia prosta jest zdefiniowana przez przecięcie dwóch płaszczyzn. Znajdź kanoniczne równania linii.

Decyzja:

Mamy równanie w postaci:

Musisz znaleźć punkt x 0, y 0, z 0), przez którą przechodzi linia prosta i wektor kierunkowy.

Jedną ze współrzędnych wybieramy arbitralnie. Na przykład, z=1, to otrzymujemy układ dwóch równań z dwiema niewiadomymi:

W ten sposób znaleźliśmy punkt leżący na pożądanej linii (2,0,1).

Jako wektor kierunkowy żądanej linii prostej przyjmujemy iloczyn poprzeczny wektorów i , które są wektorami normalnymi, ponieważ , co oznacza równolegle do żądanej linii.

Zatem wektor kierunkowy prostej ma rzuty . Korzystając z równania prostej przechodzącej przez dany punkt równolegle do danego wektora:

Tak więc pożądane równanie kanoniczne ma postać:

Przykład 8:

Znajdź współrzędne punktu przecięcia prostej i samolot 2x+3lat+3z-8=0

Decyzja:

Zapiszmy dane równanie prostej w postaci parametrycznej.

x=3t-2; y=-t+2; z=2t-1

każdy punkt prostej odpowiada pojedynczej wartości parametru t. Aby znaleźć parametr t odpowiadające punktowi przecięcia prostej i płaszczyzny, podstawiamy wyrażenie do równania płaszczyzny x, y, z poprzez parametr t.

2(3t-2)+(-t+2)+3(2t-1)-8=0

6t-4-3t+6+6t-3-8=0

t=1

następnie współrzędne żądanego punktu

żądany punkt przecięcia ma współrzędne (1;1;1).

Przykład 9:

Znajdź równanie płaszczyzny przechodzącej przez linie równoległe.

Zróbmy schematyczny rysunek (rysunek 5.9)

Rysunek 5.9

Z podanych równań prostych wyznaczamy rzuty wektorów kierujących tych prostych. Znajdujemy rzuty wektora leżącego na płaszczyźnie P i bierzemy punkty oraz z równań kanonicznych prostych M 1 (1, -1,2) i M 2 (0,1, -2).