Criterium voor lineaire afhankelijkheid van vectoren in rn. Drie soorten lineaire afhankelijkheid:

Noodzakelijke voorwaarde voor lineaire afhankelijkheid van n functies.

Laat de functies , hebben afgeleiden van de limiet (n-1).

Overweeg de determinant: (1)

W(x) wordt gewoonlijk de Wronsky-determinant voor functies genoemd.

Stelling 1. Als de functies lineair afhankelijk zijn in het interval (a,b), dan is hun Wronskian W(x) in dit interval identiek gelijk aan nul.

Een bewijs. Door de voorwaarde van de stelling, de relatie

, (2) waarbij niet alle gelijk zijn aan nul. Laten . Dan

(3). Onderscheid deze identiteit n-1 keer en,

substitueren in plaats van hun verkregen waarden in de Vronsky-determinant,

we krijgen:

In de Vronsky-determinant is de laatste kolom een ​​lineaire combinatie van de voorgaande n-1 kolommen en is daarom op alle punten van het interval (a, b) gelijk aan nul.

Stelling 2. Als de functies y 1 ,..., y n lineair onafhankelijke oplossingen zijn van de vergelijking L[y] = 0, waarvan alle coëfficiënten continu zijn in het interval (a,b), dan is de Wronskian van deze oplossingen verschillend van nul op elk puntinterval (a,b).

Een bewijs. Laten we het tegenovergestelde aannemen. Er is X 0 , waarbij W(X 0)=0. We stellen een stelsel van n vergelijkingen samen

Het is duidelijk dat systeem (5) een oplossing heeft die niet nul is. Laat (6).

Laten we een lineaire combinatie van oplossingen y 1 ,..., y n samenstellen.

Y(x) is een oplossing van de vergelijking L[y] = 0. Bovendien, . Op grond van de uniciteitsstelling mag de oplossing van de vergelijking L[y] = 0 met nul beginvoorwaarden slechts nul zijn, ᴛ.ᴇ. .

We krijgen een identiteit waarbij niet alles gelijk is aan nul, wat betekent dat y 1 ,..., y n lineair afhankelijk zijn, wat in tegenspraak is met de voorwaarde van de stelling. Daarom is er geen punt waar W(X 0)=0.

Op basis van Stelling 1 en Stelling 2 kunnen we de volgende stelling formuleren. Om ervoor te zorgen dat n oplossingen van de vergelijking L[y] = 0 lineair onafhankelijk zijn in het interval (a,b), is het uiterst belangrijk en voldoende dat hun Wronskian op geen enkel punt van dit interval verdwijnt.

De volgende voor de hand liggende eigenschappen van het Wronskiaan volgen ook uit de bewezen stellingen.

1. Als de Wronskian van n oplossingen van de vergelijking L[y] = 0 gelijk is aan nul op één punt x = x 0 uit het interval (a, b), waarin alle coëfficiënten p i (x) continu zijn, dan is het gelijk aan nul op alle ex-punten van dit interval.
2. Als de Wronskian van n oplossingen van de vergelijking L[y] = 0 niet-nul is op één punt x = x 0 van het interval (a, b), dan is het niet-nul op alle punten van dit interval.

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, voor de lineariteit van n onafhankelijke oplossingen van de vergelijking L[y] = 0 in het interval (a,b), waarin de coëfficiënten van de vergelijking p i (x) continu zijn, is het uiterst belangrijk en voldoende dat hun Wronskian zelfs in één punt van dit interval van nul verschillen.

Noodzakelijke voorwaarde voor lineaire afhankelijkheid van n functies. - concept en typen. Classificatie en kenmerken van de categorie "Een noodzakelijke voorwaarde voor de lineaire afhankelijkheid van n functies." 2017, 2018.

Scheepsbehandelingsuitrusting (vrachtuitrusting aan boord) Lezing nr. 6 Thema: Ladinguitrusting (vrachtuitrusting) 6.1. Scheepsafhandelingsapparatuur (uitrusting voor vrachtafhandeling aan boord). 6.2. Lading kranen. 6.3. helling. Overbelading is het verplaatsen van goederen van of naar een voertuig. Veel... .

Definitie 18.2 Functie systeemf, ..., f pgenaamdikik-neek o h a in en c en m. o d in de opening(a, (3) als sommige niet-triviaal 5 de lineaire combinatie van deze functies is gelijk aan nul op dit interval identiek:

Definitie 18.3 vector systeem f1 , ..., x n wordt lineair genoemd in a en c en m o d als een niet-triviale, lineaire combinatie van deze vectoren gelijk is aan de kogelvector:

L Om verwarring te voorkomen, zullen we het nummer van de vectorcomponent (vectorfunctie) aanduiden met de onderste index, en het nummer van de vector zelf (als er meerdere van dergelijke vectoren zijn) met de bovenste.

"We herinneren je eraan dat een lineaire combinatie niet-triviaal wordt genoemd als niet alle coëfficiënten erin nul zijn.

Definitie 18.4 Het stelsel van vectorfuncties x 1 ^),..., x n (t) heet lineair h en in en met en mijn ongeveer th op het interval,(a, /3) als een niet-triviale lineaire combinatie van deze vectorfuncties identiek gelijk is aan de nulvector op dit interval:

Het is belangrijk om de samenhang van deze drie concepten (lineaire afhankelijkheid van functies, vectoren en vectorfuncties) met elkaar te begrijpen.

Allereerst, als we formule (18.6) in uitgebreide vorm presenteren (onthoud dat elk van xg (1) is een vector)

dan is het gelijk aan het systeem van gelijkheden

wat betekent lineaire afhankelijkheid van de rde componenten in de zin van de eerste definitie (als functies). Er wordt gezegd dat de lineaire afhankelijkheid van vectorfuncties impliceert dat hun component voor component lineaire afhankelijkheid.

Het omgekeerde is over het algemeen niet waar: het volstaat om het voorbeeld van een paar vectorfuncties te beschouwen

De eerste componenten van deze vectorfuncties vallen eenvoudig samen, wat betekent dat ze lineair afhankelijk zijn. De tweede componenten zijn proportioneel, dus. zijn ook lineair afhankelijk. Als we echter proberen hun lineaire combinatie gelijk aan nul identiek te construeren, dan uit de relatie

krijg het systeem onmiddellijk

die de enige oplossing heeft C - C-2 - 0. Onze vectorfuncties zijn dus lineair onafhankelijk.

Wat is de reden voor zo'n vreemde eigenschap? Wat is de truc waarmee je lineair onafhankelijke vectorfuncties kunt bouwen van bewust afhankelijke functies?

Het blijkt dat het hele punt niet zozeer zit in de lineaire afhankelijkheid van de componenten, maar in de verhouding van coëfficiënten die nodig is om nul te verkrijgen. In het geval van een lineaire afhankelijkheid van vectorfuncties, bedient dezelfde set coëfficiënten alle componenten, ongeacht het aantal. Maar in ons voorbeeld was voor de ene component een deel van de coëfficiënten vereist en voor de andere een andere. De truc is dus heel eenvoudig: om een ​​lineaire afhankelijkheid van de gehele vectorfuncties te verkrijgen uit een "component-voor-component" lineaire afhankelijkheid, is het noodzakelijk dat alle componenten lineair afhankelijk zijn "in dezelfde verhouding".

Laten we ons nu richten op de studie van de relatie tussen de lineaire afhankelijkheid van vectorfuncties en vectoren. Hier is het bijna duidelijk dat de lineaire afhankelijkheid van de vectorfuncties impliceert dat voor elke vaste t* vector

lineair afhankelijk zal zijn.

Het omgekeerde geldt in het algemeen niet: van de lineaire afhankelijkheid van de vectoren voor elk t volgt geen lineaire afhankelijkheid van vectorfuncties. Dit is gemakkelijk te zien in het voorbeeld van twee vectorfuncties

Bij t=1, t=2 en t=3 we krijgen paren vectoren

respectievelijk. Elk paar vectoren is proportioneel (met respectievelijk coëfficiënten 1,2 en 3). Het is gemakkelijk te zien dat voor elke vaste t* ons paar vectoren zal evenredig zijn met de coëfficiënt t*.

Als we een lineaire combinatie van vectorfuncties proberen te construeren die identiek gelijk is aan nul, dan geven de eerste componenten ons al de relatie

wat alleen mogelijk is als VAN = VAN2 = 0. Onze vectorfuncties bleken dus lineair onafhankelijk te zijn. Nogmaals, de verklaring voor dit effect is dat in het geval van een lineaire afhankelijkheid van vectorfuncties, dezelfde set constanten Cj alle waarden bedient t, en in ons voorbeeld voor elke waarde t vereist zijn eigen verhouding tussen de coëfficiënten.

Door ons geïntroduceerd lineaire bewerkingen op vectoren het mogelijk maken om verschillende uitdrukkingen te creëren voor vector hoeveelheden en transformeer ze met behulp van de eigenschappen die voor deze bewerkingen zijn ingesteld.

Op basis van een gegeven set vectoren a 1 , ... en n , kun je een uitdrukking van de vorm samenstellen

waarbij a 1 , ... en n willekeurige reële getallen zijn. Deze uitdrukking heet lineaire combinatie van vectoren een 1 , ..., een n . Getallen α i , ik = 1, n , are lineaire combinatiecoëfficiënten. De verzameling vectoren wordt ook wel vector systeem.

In verband met het geïntroduceerde concept van een lineaire combinatie van vectoren, rijst het probleem van het beschrijven van de verzameling vectoren die kan worden geschreven als een lineaire combinatie van een gegeven systeem van vectoren a 1 , ..., a n . Daarnaast zijn vragen over de voorwaarden waaronder er een representatie is van een vector in de vorm van een lineaire combinatie, en over de uniciteit van zo'n representatie, vanzelfsprekend.

Definitie 2.1. Vectoren a 1 , ... en n heten lineair afhankelijk, als er zo'n verzameling coëfficiënten is α 1 , ... , α n dat

α 1 een 1 + ... + α n een n = 0 (2.2)

en ten minste één van deze coëfficiënten is niet nul. Als de gespecificeerde set coëfficiënten niet bestaat, worden de vectoren genoemd lineair onafhankelijk.

Als α 1 = ... = α n = 0, dan is natuurlijk α 1 a 1 + ... + α n a n = 0. Met dit in gedachten kunnen we dit zeggen: vectoren a 1 , ..., en n zijn lineair onafhankelijk als uit gelijkheid (2.2) volgt dat alle coëfficiënten α 1 , ... , α n gelijk zijn aan nul.

De volgende stelling legt uit waarom het nieuwe concept de term "afhankelijkheid" (of "onafhankelijkheid") wordt genoemd, en geeft een eenvoudig criterium voor lineaire afhankelijkheid.

Stelling 2.1. Om ervoor te zorgen dat de vectoren a 1 , ... en n , n > 1, lineair afhankelijk zijn, is het noodzakelijk en voldoende dat een van hen een lineaire combinatie van de andere is.

◄ Noodzaak. Neem aan dat de vectoren a 1 , ... en n lineair afhankelijk zijn. Volgens definitie 2.1 van lineaire afhankelijkheid is er in gelijkheid (2.2) ten minste één coëfficiënt die niet nul is aan de linkerkant, bijvoorbeeld α 1 . We laten de eerste term aan de linkerkant van de gelijkheid, we verplaatsen de rest naar de rechterkant en veranderen hun tekens zoals gewoonlijk. Als we de resulterende gelijkheid delen door α 1 , krijgen we

een 1 =-α 2 /α 1 ⋅ een 2 - ... - α n / α 1 ⋅ een n

die. weergave van de vector a 1 als een lineaire combinatie van de overige vectoren a 2 , ... en n .

geschiktheid. Laat bijvoorbeeld de eerste vector a 1 worden weergegeven als een lineaire combinatie van de overige vectoren: a 1 = β 2 a 2 + ... + β n a n . Als we alle termen van de rechterkant naar de linkerkant overbrengen, krijgen we a 1 - β 2 a 2 - ... - β n a n = 0, d.w.z. lineaire combinatie van vectoren a 1 , ..., en n met coëfficiënten α 1 = 1, α 2 = - β 2 , ..., α n = - β n , gelijk aan nulvector. In deze lineaire combinatie zijn niet alle coëfficiënten gelijk aan nul. Volgens definitie 2.1 zijn de vectoren a 1 , ... en n lineair afhankelijk.

De definitie en het criterium van lineaire afhankelijkheid zijn zo geformuleerd dat ze de aanwezigheid van twee of meer vectoren impliceren. Men kan echter ook spreken van een lineaire afhankelijkheid van één vector. Om deze mogelijkheid te realiseren, moeten we in plaats van "vectoren zijn lineair afhankelijk" zeggen "het systeem van vectoren is lineair afhankelijk". Het is gemakkelijk in te zien dat de uitdrukking "een systeem van één vector lineair afhankelijk is" betekent dat deze enkele vector nul is (er is slechts één coëfficiënt in een lineaire combinatie en deze mag niet gelijk zijn aan nul).

Het concept van lineaire afhankelijkheid heeft een eenvoudige geometrische interpretatie. Deze interpretatie wordt verduidelijkt door de volgende drie uitspraken.

Stelling 2.2. Twee vectoren zijn lineair afhankelijk dan en slechts dan als ze collineair.

◄ Als de vectoren a en b lineair afhankelijk zijn, dan wordt de ene, bijvoorbeeld a, uitgedrukt door de andere, d.w.z. a = λb voor een reëel getal λ. Volgens definitie 1.7 werken vectoren door een getal, de vectoren a en b zijn collineair.

Laat nu de vectoren a en b collineair zijn. Als ze allebei nul zijn, is het duidelijk dat ze lineair afhankelijk zijn, aangezien elke lineaire combinatie ervan gelijk is aan de nulvector. Laat een van deze vectoren niet gelijk zijn aan 0, bijvoorbeeld de vector b. Geef met λ de verhouding van de lengtes van de vectoren aan: λ = |а|/|b|. Collineaire vectoren kunnen zijn unidirectioneel of tegengestelde richtingen. In het laatste geval veranderen we het teken van λ. Als we dan Definitie 1.7 controleren, zien we dat a = λb. Volgens Stelling 2.1 zijn de vectoren a en b lineair afhankelijk.

Opmerking 2.1. In het geval van twee vectoren, rekening houdend met het criterium van lineaire afhankelijkheid, kan de bewezen stelling als volgt worden geherformuleerd: twee vectoren zijn collineair als en slechts als een van hen wordt weergegeven als het product van de andere door een getal. Dit is een handig criterium voor de collineariteit van twee vectoren.

Stelling 2.3. Drie vectoren zijn lineair afhankelijk dan en slechts dan als ze coplanair.

◄ Als drie vectoren a, b, c lineair afhankelijk zijn, dan is volgens Stelling 2.1 een daarvan, bijvoorbeeld a, een lineaire combinatie van de andere: a = βb + γc. Laten we de oorsprong van vectoren b en c combineren in punt A. Dan zullen de vectoren βb, γc een gemeenschappelijke oorsprong hebben in punt A en parallellogram regel hun som, die. vector a, zal een vector zijn met het begin A en einde, wat het hoekpunt is van een parallellogram dat is gebouwd op summandvectoren. Alle vectoren liggen dus in hetzelfde vlak, dat wil zeggen dat ze coplanair zijn.

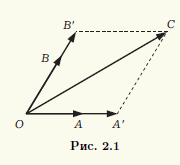
Laat de vectoren a, b, c coplanair zijn. Als een van deze vectoren nul is, ligt het voor de hand dat het een lineaire combinatie van de andere is. Het volstaat om alle coëfficiënten van de lineaire combinatie gelijk aan nul te nemen. Daarom kunnen we aannemen dat alle drie vectoren niet nul zijn. Compatibel begin deze vectoren op een gemeenschappelijk punt O. Laten hun uiteinden respectievelijk de punten A, B, C zijn (Fig. 2.1). Trek lijnen door punt C evenwijdig aan lijnen die door paren punten O, A en O, B gaan. Door de snijpunten aan te duiden met A" en B", krijgen we een parallellogram OA"CB", dus OC" = OA" + OB " . Vector OA" en de niet-nul vector a= OA zijn collineair, en daarom kan de eerste worden verkregen door het tweede te vermenigvuldigen met een reëel getal α:OA" = αOA. Evenzo, OB" = βOB , β ∈ R. Als resultaat krijgen we dat OC" = α OA + βOB , d.w.z. de vector c is een lineaire combinatie van de vectoren a en b. Volgens Stelling 2.1 zijn de vectoren a, b, c lineair afhankelijk.

Stelling 2.4. Elke vier vectoren zijn lineair afhankelijk.

◄ Het bewijs volgt hetzelfde schema als in Stelling 2.3. Beschouw willekeurige vier vectoren a, b, c en d. Als een van de vier vectoren nul is, of als er twee collineaire vectoren zijn, of als drie van de vier vectoren coplanair zijn, dan zijn deze vier vectoren lineair afhankelijk. Als vectoren a en b bijvoorbeeld collineair zijn, kunnen we hun lineaire combinatie αa + βb = 0 samenstellen met coëfficiënten die niet gelijk zijn aan nul, en dan de resterende twee vectoren bij deze combinatie optellen, waarbij we nullen als coëfficiënten nemen. We krijgen een lineaire combinatie van vier vectoren gelijk aan 0, waarin er coëfficiënten zijn die niet nul zijn.

We kunnen dus aannemen dat er onder de vier gekozen vectoren geen nul-en zijn, geen twee collineair en geen drie coplanair. We kiezen als gemeenschappelijk begin punt O. Dan zullen de uiteinden van de vectoren a, b, c, d enkele punten A, B, C, D zijn (Fig. 2.2). Door punt D trekken we drie vlakken evenwijdig aan de vlakken ОВС, OCA, OAB, en laten A", B", С" de snijpunten zijn van deze vlakken met respectievelijk de lijnen OA, OB, OS. We krijgen een parallellepipedum OA"C"B"C" B"DA", en de vectoren a, b, c liggen op de randen die uit het hoekpunt O komen. Aangezien de vierhoek OC"DC" een parallellogram is, dan is OD = OC" + OC " . Op zijn beurt is het segment OS" een diagonaal parallellogram OA"C"B", dus OC" = OA" + OB" en OD = OA" + OB" + OC" .

Er moet nog worden opgemerkt dat de vectorparen OA ≠ 0 en OA" , OB ≠ 0 en OB" , OC ≠ 0 en OC" collineair zijn, en daarom kunnen we de coëfficiënten α, β, γ kiezen zodat OA" = αOA , OB" = βOB en OC" = γOC . Ten slotte krijgen we OD = αOA + βOB + γOC . Bijgevolg wordt de vector OD uitgedrukt in termen van de resterende drie vectoren, en alle vier vectoren, volgens Stelling 2.1, zijn lineair afhankelijk.

Een noodzakelijke en voldoende voorwaarde voor de lineaire afhankelijkheid van twee

vectoren is hun collineariteit.

2. Scalair product- een bewerking op twee vectoren, waarvan het resultaat een scalair (getal) is dat niet afhankelijk is van het coördinatensysteem en de lengtes van de vermenigvuldigingsvectoren en de hoek daartussen karakteriseert. Deze bewerking komt overeen met de vermenigvuldiging lengte gegeven vector x op projectie een andere vector y naar de gegeven vector x. Deze bewerking wordt meestal gezien als commutatief en lineair in elke factor.

Eigenschappen van het puntproduct:

3. Drie vectoren (of meer) heten coplanair als ze, teruggebracht tot een gemeenschappelijke oorsprong, in hetzelfde vlak liggen.

Een noodzakelijke en voldoende voorwaarde voor de lineaire afhankelijkheid van drie vectoren is hun coplanariteit.Elke vier vectoren zijn lineair afhankelijk. basis in de ruimte elke geordende triple van niet-coplanaire vectoren wordt genoemd. Een basis in de ruimte maakt het mogelijk om ondubbelzinnig met elke vector een geordend drievoud van getallen te associëren - de coëfficiënten van de representatie van deze vector in een lineaire combinatie van vectoren van de basis. Integendeel, met behulp van een basis zullen we een vector associëren met elk geordend triplet van getallen als we een lineaire combinatie maken.Een orthogonale basis heet orthonormaal , als de vectoren gelijk zijn aan één in lengte. Voor een orthonormale basis in de ruimte wordt vaak de notatie gebruikt. Stelling: In een orthonormale basis zijn de coördinaten van vectoren de corresponderende orthogonale projecties van deze vector op de richtingen van de coördinaatvectoren. Een triple van niet-coplanaire vectoren a, b, c genaamd Rechtsaf, als de waarnemer van hun gemeenschappelijke oorsprong de uiteinden van de vectoren omzeilt a, b, c in die volgorde lijkt het met de klok mee te gaan. Anders a, b, c - links triple. Alle rechter (of linker) triples van vectoren heten gelijk georiënteerd. Een rechthoekig coördinatenstelsel op een vlak wordt gevormd door twee onderling loodrechte coördinaatassen OS en OY. De coördinaatassen snijden elkaar in een punt O, die de oorsprong wordt genoemd, heeft elke as een positieve richting. BIJ rechter hand coördinatensysteem, wordt de positieve richting van de assen zo gekozen dat met de richting van de as OY omhoog, as OS keek naar rechts.

Vier hoeken (I, II, III, IV) gevormd door de coördinaatassen X"X en ja"ja, worden coördinaathoeken genoemd of kwadranten(zie afb. 1).

als de vectoren en met betrekking tot een orthonormale basis op het vlak respectievelijk coördinaten hebben en, dan wordt het scalaire product van deze vectoren berekend met de formule

4. Vectorproduct van twee vectoren a en b is een bewerking op hen, alleen gedefinieerd in de driedimensionale ruimte, waarvan het resultaat is vector met het volgende

eigendommen:

De geometrische betekenis van het uitwendige product van vectoren is het gebied van een parallellogram gebouwd op vectoren. Een noodzakelijke en voldoende voorwaarde voor de collineariteit van een vector die niet nul is en een vector is het bestaan ​​van een getal dat aan de gelijkheid voldoet.

Als twee vectoren en worden gedefinieerd door hun rechthoekige Cartesiaanse coördinaten, of nauwkeuriger, worden ze weergegeven in een vorthonormalized basis

en het coördinatensysteem klopt, dan heeft hun vectorproduct de vorm

Om deze formule te onthouden, is het handig om de determinant te gebruiken:

5. Gemengd product vectoren - het scalaire product van een vector en het uitwendige product van vectoren en:

Soms heet het drievoudig scalair product vectoren, blijkbaar vanwege het feit dat het resultaat een scalair is (meer precies, een pseudoscalair).

Geometrische zin: De module van het gemengde product is numeriek gelijk aan het volume van het parallellepipedum gevormd door de vectoren.

Wanneer twee factoren worden verwisseld, verandert het gemengde product van teken in het tegenovergestelde:

Bij een cyclische (cirkelvormige) permutatie van factoren verandert het gemengde product niet:

Het gemengde product is lineair in elke factor.

Het gemengde product is nul als en slechts als de vectoren coplanair zijn.

1. Compplanariteitsvoorwaarde voor vectoren: drie vectoren zijn coplanair als en slechts als hun gemengde product nul is.

§ Een drietal vectoren dat een paar collineaire vectoren bevat, is coplanair.

§ Gemengd product van coplanaire vectoren. Dit is een criterium voor de coplanariteit van drie vectoren.

§ Coplanaire vectoren zijn lineair afhankelijk. Dit is ook een criterium voor coplanariteit.

§ Er zijn reële getallen zodat voor coplanair , behalve voor of . Dit is een herformulering van de vorige eigenschap en is ook een criterium voor coplanariteit.

§ In een 3-dimensionale ruimte vormen 3 niet-coplanaire vectoren een basis. Dat wil zeggen, elke vector kan worden weergegeven als: . Dan zullen de coördinaten in de gegeven basis zijn.

Het gemengde product in het rechter Cartesiaanse coördinatenstelsel (in de orthonormale basis) is gelijk aan de determinant van de matrix bestaande uit de vectoren en :

§6. Algemene vergelijking (compleet) van het vlak

waarbij en bovendien constanten zijn en niet tegelijkertijd gelijk zijn aan nul; in vectorvorm:

waar is de straalvector van het punt , de vector staat loodrecht op het vlak (normale vector). Richting cosinus vector:

Als een van de coëfficiënten in de vlakke vergelijking nul is, wordt de vergelijking genoemd incompleet. Wanneer het vlak door de oorsprong van coördinaten gaat, wanneer (of , ) P. evenwijdig is aan de as (respectievelijk of ). Voor ( , of ) is het vlak evenwijdig aan het vlak (respectievelijk of ).

§ Vergelijking van een vlak in segmenten:

waar , , zijn de segmenten afgesneden door het vlak op de assen en .

§ Vergelijking van een vlak dat door een punt gaat loodrecht op de normaalvector :

in vectorvorm:

(gemengd product van vectoren), anders

§ Normale (genormaliseerde) vlakvergelijking

§ Hoek tussen twee vlakken. Als de P.-vergelijkingen worden gegeven in de vorm (1), dan

Indien in vectorvorm, dan

§ Vliegtuigen zijn parallel, als

Of (vectorproduct)

§ Vliegtuigen staan ​​loodrecht, als

Of . (Scalair product)

7. Vergelijking van een vlak dat door drie gegeven punten gaat , niet op dezelfde lijn liggen:

8. De afstand van een punt tot een vlak is de kleinste van de afstanden tussen dit punt en de punten van het vlak. Het is bekend dat de afstand van een punt tot een vlak gelijk is aan de lengte van de loodlijn die van dit punt naar het vlak valt.

§ Punt afwijking: uit het vlak gegeven door de genormaliseerde vergelijking

Als en de oorsprong aan weerszijden van het vlak liggen, anders . De afstand van een punt tot een vlak is

§ De afstand van het punt tot het vlak gegeven door de vergelijking wordt berekend met de formule:

9. Vliegtuig bundel- de vergelijking van elke P. die door de snijlijn van twee vlakken gaat

waarbij α en β alle getallen zijn die niet tegelijkertijd gelijk zijn aan nul.

Om de drie vlakken gedefinieerd door hun algemene vergelijkingen A 1 x+B 1 y+C 1 z+D 1 =0, A 2 x+B 2 y+C 2 z+D 2 =0, A 3 x+B 3 y+C 3 z+D 3 =0 met betrekking tot PDSC behoorde tot één straal, goed of ongepast, het is noodzakelijk en voldoende dat de rangorde van de matrix gelijk is aan twee of één.
Stelling 2. Laat twee vlakken π 1 en π 2 gegeven worden met betrekking tot PDSC door hun algemene vergelijkingen: A 1 x+B 1 y+C 1 z+D 1 =0, A 2 x+B 2 y+C 2 z +D2 = 0. Om ervoor te zorgen dat het π 3 vlak, gegeven ten opzichte van de PDSC door zijn algemene vergelijking A 3 x+B 3 y+C 3 z+D 3 =0, behoort tot de straal gevormd door de π 1 en π 2 vlakken, moet het is noodzakelijk en voldoende dat de linkerkant van de vergelijking van het vlak π 3 werd weergegeven als een lineaire combinatie van de linker delen van de vergelijkingen van de vlakken π 1 en π 2 .

10.Vectorparametrische vergelijking van een rechte lijn in de ruimte:

waar is de straalvector van een vast punt M 0 liggend op een rechte lijn is een vector die niet nul is collineair aan deze rechte lijn, is de straalvector van een willekeurig punt op de rechte lijn.

Parametrische vergelijking van een rechte lijn in de ruimte:

M

Canonieke vergelijking van een rechte lijn in de ruimte:

waar zijn de coördinaten van een vast punt? M 0 liggend op een rechte lijn; - coördinaten van een vector collineair aan deze lijn.

Algemene vectorvergelijking van een rechte lijn in de ruimte:

Aangezien de lijn het snijpunt is van twee verschillende niet-parallelle vlakken, respectievelijk gegeven door de algemene vergelijkingen:

dan kan de vergelijking van een rechte lijn worden gegeven door een stelsel van deze vergelijkingen:

De hoek tussen de richtingsvectoren en zal gelijk zijn aan de hoek tussen de lijnen. De hoek tussen vectoren wordt gevonden met behulp van het scalaire product. cosA=(ab)/IaI*IbI

De hoek tussen een rechte lijn en een vlak wordt gevonden met de formule:

Voorwaarden voor parallellisme van twee lijnen:

a) Als de lijnen worden gegeven door vergelijkingen (4) met een helling, dan is de noodzakelijke en voldoende voorwaarde voor hun parallellisme de gelijkheid van hun hellingen:

k 1 = k 2 . (8)

b) Voor het geval dat de lijnen worden gegeven door vergelijkingen in algemene vorm (6), is de noodzakelijke en voldoende voorwaarde voor hun parallellisme dat de coëfficiënten op de corresponderende stroomcoördinaten in hun vergelijkingen proportioneel zijn, d.w.z.

Voorwaarden voor loodrechtheid van twee lijnen:

a) In het geval dat de lijnen worden gegeven door vergelijkingen (4) met een helling, is de noodzakelijke en voldoende voorwaarde voor hun loodrechtheid dat hun hellingen wederkerig zijn in grootte en tegengesteld in teken, d.w.z.

b) Als de vergelijkingen van rechte lijnen in algemene vorm (6) worden gegeven, dan is de voorwaarde voor hun loodrechtheid (noodzakelijk en voldoende) om aan de gelijkheid te voldoen

EEN 1 EEN 2 + B 1 B 2 = 0. (12)

Een lijn heet loodrecht op een vlak als ze loodrecht staat op een lijn in dat vlak. Als een lijn loodrecht staat op elk van de twee snijdende lijnen van een vlak, dan staat ze loodrecht op dat vlak. Om een ​​lijn en een vlak evenwijdig te laten zijn, is het noodzakelijk en voldoende dat de normaalvector op het vlak en de richtingsvector van de lijn loodrecht staan. Hiervoor is het noodzakelijk dat hun scalair product gelijk is aan nul.

Om een ​​lijn en een vlak loodrecht te laten zijn, is het noodzakelijk en voldoende dat de normaalvector op het vlak en de richtingsvector van de lijn collineair zijn. Aan deze voorwaarde is voldaan als het uitwendige product van deze vectoren gelijk was aan nul.

12. In de ruimte, de afstand van een punt tot een rechte lijn gegeven door een parametervergelijking

kan worden gevonden als de minimale afstand van een bepaald punt tot een willekeurig punt op een rechte lijn. Coëfficiënt t dit punt kan worden gevonden door de formule

Afstand tussen snijdende lijnen is de lengte van hun gemeenschappelijke loodlijn. Het is gelijk aan de afstand tussen evenwijdige vlakken die door deze lijnen gaan.

zeker Systeem van elementen x 1 ,…,x m lin. productie V heet lineair afhankelijk als ∃ λ 1 ,…, λ m ∈ ℝ (|λ 1 |+…+| λ m | ≠ 0) zodat λ 1 x 1 +…+ λ m x m = θ .

zeker Een stelsel van elementen x 1 ,…,x m ∈ V heet lineair onafhankelijk als uit de gelijkheid λ 1 x 1 +…+ λ m x m = θ ⟹λ 1 =…= λ m =0.

zeker Een element x ∈ V heet een lineaire combinatie van elementen x 1 ,…,x m ∈ V als ∃ λ 1 ,…, λ m ∈ ℝ zodanig dat x= λ 1 x 1 +…+ λ m x m .

Stelling (criterium van lineaire afhankelijkheid): Een stelsel van vectoren x 1 ,…,x m ∈ V is lineair afhankelijk dan en slechts dan als ten minste één vector van het stelsel lineair wordt uitgedrukt in termen van de andere.

dok. Nodig hebben: Zij x 1 ,…,x m lineair afhankelijk ⟹ ∃ λ 1 ,…, λ m ∈ ℝ (|λ 1 |+…+| λ m | ≠ 0) zodat λ 1 x 1 +…+ λ m -1 x m -1 + m x m = . Stel λ m ≠ 0, dan

x m \u003d (-) x 1 + ... + (-) x m -1.

geschiktheid: Laat minstens één van de vectoren lineair uitgedrukt worden in termen van de rest van de vectoren: x m = λ 1 x 1 +…+ λ m -1 x m -1 (λ 1 ,…, λ m -1 ∈ ℝ) λ 1 x 1 +…+ λ m -1 x m -1 +(-1) x m =0 λ m =(-1) ≠ 0 ⟹ x 1 ,…,x m - zijn lineair onafhankelijk.

Ven. lineaire afhankelijkheidsvoorwaarde:

Als het systeem een ​​nul-element of een lineair afhankelijk subsysteem bevat, dan is het lineair afhankelijk.

λ 1 x 1 +…+ λ m x m = 0 – lineair afhankelijk systeem

1) Zij x 1 = θ, dan geldt deze gelijkheid voor λ 1 =1 en λ 1 =…= λ m =0.

2) Zij λ 1 x 1 +…+ λ m x m =0 een lineair afhankelijk subsysteem ⟹|λ 1 |+…+| m | 0 . Dan krijgen we voor λ 1 =0 ook |λ 1 |+…+| m | ≠ 0 ⟹ λ 1 x 1 +…+ λ m x m =0 is een lineair afhankelijk systeem.

Basis van een lineaire ruimte. Vectorcoördinaten in de gegeven basis. De coördinaten van de som van vectoren en het product van een vector door een getal. Noodzakelijke en voldoende voorwaarde voor lineaire afhankelijkheid van een stelsel van vectoren.

Definitie: Een geordend systeem van elementen e 1, ..., e n van een lineaire ruimte V heet een basis van deze ruimte als:

A) e 1 ... e n zijn lineair onafhankelijk

B) ∀ x ∈ α 1 … α n zodat x= α 1 e 1 +…+ α n e n

x= α 1 e 1 +…+ α n e n – uitbreiding van het element x in de basis e 1, …, e n

α 1 … α n ∈ ℝ zijn de coördinaten van het element x in de basis e 1, …, e n

Stelling: Als de basis e 1, …, en n gegeven is in de lineaire ruimte V, dan is ∀ x ∈ V de coördinatenkolom x in de basis e 1, …, en n uniek bepaald (de coördinaten zijn uniek bepaald)

Een bewijs: Zij x=α 1 e 1 +…+ α n e n en x=β 1 e 1 +…+β n e n

x= ⇔ = Θ, d.w.z. e 1, …, en n zijn lineair onafhankelijk, dan - =0 ∀ i=1, …, n ⇔ = ∀ i=1, …, n h.t.d.

Stelling: laat e 1, …, e n de basis zijn van de lineaire ruimte V; x, y zijn willekeurige elementen van de ruimte V, λ ∈ ℝ is een willekeurig getal. Wanneer x en y worden opgeteld, worden hun coördinaten opgeteld, wanneer x wordt vermenigvuldigd met λ, worden de coördinaten van x ook vermenigvuldigd met λ.

Een bewijs: x= (e 1, …, e n) en y= (e 1, …, e n)

x+y= + = (e 1, …, e n)

λx= λ ) = (e 1, …, e n)

Lemma1: (noodzakelijke en voldoende voorwaarde voor de lineaire afhankelijkheid van een stelsel van vectoren)

Laat e ​​1 …e n de basis zijn van de ruimte V. Het systeem van elementen f 1 , …, f k ∈ V is lineair afhankelijk dan en slechts dan als de coördinaatkolommen van deze elementen in de basis e 1, …, e n zijn lineair afhankelijk

Een bewijs: uitbreiden f 1 , …, f k in de basis e 1, …, e n

f m =(e 1, …, e n) m=1, …, k

λ 1 f 1 +…+λ k f k =(e 1, …, e n)[ λ 1 +…+ λ n ] d.w.z. λ 1 f 1 +…+λ k f k = Θ ⇔

⇔ λ 1 +…+ λ n = zoals vereist.

13. Afmeting van een lineaire ruimte. Stelling over de relatie tussen dimensie en basis.
Definitie: Een lineaire ruimte V wordt een n-dimensionale ruimte genoemd als er n lineair onafhankelijke elementen in V zijn, en een systeem van n + 1 elementen van de ruimte V lineair afhankelijk is. In dit geval wordt n de afmeting van de lineaire ruimte V genoemd en wordt aangeduid als dimV=n.

Een lineaire ruimte wordt oneindig-dimensionaal genoemd als ∀N ∈ ℕ in de ruimte V een lineair onafhankelijk systeem bestaat met N elementen.

Stelling: 1) Als V een n-dimensionale lineaire ruimte is, dan vormt elk geordend systeem van n lineair onafhankelijke elementen van deze ruimte een basis. 2) Als er in de lineaire ruimte V een basis is die bestaat uit n elementen, dan is de afmeting van V gelijk aan n (dimV=n).

Een bewijs: 1) Zij dimV=n ⇒ in V ∃ n lineair onafhankelijke elementen e 1, …,e n . We bewijzen dat deze elementen een basis vormen, dat wil zeggen, we bewijzen dat ∀ x ∈ V kan worden uitgebreid in termen van e 1, …,en . Laten we er x bij optellen: e 1, …,e n , x – dit systeem bevat n+1 vectoren, wat betekent dat het lineair afhankelijk is. Aangezien e 1, …,e n lineair onafhankelijk is, dan is volgens Stelling 2 x lineair uitgedrukt door e 1, …,e n i.e. ∃ ,…, zodat x= α 1 e 1 +…+ α n e n . Dus e 1, …,e n is de basis van de ruimte V. 2) Laat e ​​1, …,e n de basis zijn van V, dus er zijn n lineair onafhankelijke elementen in V ∃ n. Neem willekeurige f 1 ,…,f n ,f n +1 ∈ V – n+1 elementen. Laten we hun lineaire afhankelijkheid laten zien. Laten we ze opsplitsen in termen van:

f m =(e 1, …,e n) = waarbij m = 1,…,n Laten we een matrix van coördinaatkolommen maken: A= Matrix bevat n rijen ⇒ RgA≤n. Aantal kolommen n+1 > n ≥ RgA ⇒ Kolommen van matrix A (dwz kolommen met coördinaten f 1 ,…,f n ,f n +1) zijn lineair afhankelijk. Van Lemma 1 zijn ⇒ ,…,f n ,f n +1 lineair afhankelijk ⇒ dimV=n.

Gevolg: Als een basis n elementen bevat, dan bevat elke andere basis van deze ruimte n elementen.

Stelling 2: Als het stelsel van vectoren x 1 ,… ,x m -1 , x m lineair afhankelijk is, en het subsysteem x 1 ,… ,x m -1 lineair onafhankelijk is, dan wordt x m - lineair uitgedrukt door x 1 ,… ,x m -1

Een bewijs: Omdat x 1 ,… ,x m -1 , x m is lineair afhankelijk, dan is ∃ , …, , ,

, …, | , | zoals dat . Als , , ..., | => x 1 ,… ,x m -1 zijn lineair onafhankelijk, wat niet kan. Dus m = (-) x 1 +…+ (-) x m -1.