Hoe de mzf van een goniometrische functie te vinden. Oplossing van typische taken
D(v)- die waarden die het argument kan aannemen, d.w.z. functiebereik:.
E(v)- die waarden die de functie kan aannemen, d.w.z. set functiewaarden.
Methoden voor het vinden van de reeksen van functies.
sequentiële bevinding van waarden van complexe functieargumenten;
score/grensmethode;
gebruik van eigenschappen van continuïteit en monotoniciteit van een functie;
gebruik van een derivaat;
met behulp van de grootste en kleinste waarden van de functie;
grafische methode;
parameter introductie methode;
inverse functie methode.
Laten we er een paar bekijken.
De afgeleide gebruiken
Algemene benadering om de reeks waarden van een continue functie f(x) te vinden, is om de grootste en kleinste waarden van de functie f(x) in zijn domein te vinden (of om te bewijzen dat een of beide niet bestaan) .
Als u de reeks waarden van een functie moet vinden op het segment:
vind de afgeleide van de gegeven functie f "(x);
zoek de kritische punten van de functie f(x) en kies die welke bij het gegeven segment horen;
bereken de waarden van de functie aan de uiteinden van het segment en op geselecteerde kritieke punten;
selecteer onder de gevonden waarden de kleinste en grootste waarden;
Tussen deze waarden wordt de set functiewaarden afgesloten.
Als het bereik van de functie is interval, dan wordt hetzelfde schema gebruikt, maar in plaats van de waarden aan de uiteinden, worden de limieten van de functie gebruikt wanneer het argument naar de uiteinden van het interval neigt. Grenswaarden vanaf zijn niet opgenomen in de ingestelde waarde.
Grens/score methode
Om de set functiewaarden te vinden, zoekt u eerst de set argumentwaarden en vervolgens de bijbehorende minimum- en maximumwaarden van de functiefunctie. Ongelijkheden gebruiken - bepaal de grenzen.
De essentie is om de continue functie van onder en van boven te schatten en te bewijzen dat de functie de onder- en bovengrenzen van de schattingen bereikt. In dit geval wordt het samenvallen van de reeks waarden van de functie met het interval van de ondergrens van de schatting tot de bovenste bepaald door de continuïteit van de functie en de afwezigheid van andere waarden ervoor.
Eigenschappen van een continue functie
Een andere optie is om de functie om te zetten in een continue monotone functie, waarna met behulp van de eigenschappen van ongelijkheden de reeks waarden van de nieuw verkregen functie wordt geschat.
Opeenvolgend Waarden van complexe functieargumenten vinden
Gebaseerd op het sequentiële zoeken naar de reeks waarden van tussenfuncties waaruit de functie bestaat
Bereik van elementaire basisfuncties
| Functie | Veel waarden |
|---|---|
| $y = kx+ b$ | E(y) = (-∞;+∞) |
| $y = x^(2n)$ | E(y) = |
| $y = \cos(x)$ | E(j) = [-1;1] |
| $y = (\rmtg)\, x$ | E(y) = (-∞;+∞) |
| $y = (\rm ctg)\, x$ | E(y) = (-∞;+∞) |
| $y = \arcsin(x)$ | E(y) = [-π/2; π/2] |
| $y = \arccos(x)$ | E(y) = |
| $y = (\rm arctg)\, x$ | E(y) = (-π/2; π/2) |
| $y = (\rm arcctg)\, x$ | E(y) = (0; ) |
Voorbeelden
Zoek de set functiewaarden:
De afgeleide gebruiken
Zoek het definitiedomein: D(f)=[-3;3], omdat $9-x^(2)\geq 0$
Zoek de afgeleide: $f"(x)=-\frac(x)(\sqrt(9-x^(2)))$
f"(x) = 0 als x = 0. f"(x) bestaat niet als $\sqrt(9-x^(2))=0$ d.w.z. voor x = ±3. We krijgen drie kritieke punten: x 1 \u003d -3, x 2 \u003d 0, x 3 \u003d 3, waarvan er twee samenvallen met de uiteinden van het segment. Bereken: f(–3) = 0, f(0) = 3, f(3) = 0. Dus de kleinste waarde van f(x) is 0, de grootste waarde is 3.
Antwoord: E(f) = .
GEEN afgeleide gebruiken
Zoek de grootste en kleinste waarden van de functie:
sinds $
f(x) = 1-\cos^(2)(x)+\cos(x)-\frac(1)(2) =
= 1-\frac(1)(2)+\frac(1)(4)-(\cos^(2)(x)-2\cdot\cos(x)\cdot\frac(1)(2) +(\frac(1)(2))^2) =
= \frac(3)(4)-(\cos(x)-\frac(1)(2))^(2) $ , dan:
$f(x)\leq \frac(3)(4)$ voor alle x;
$f(x)\geq \frac(3)(4)-(\frac(3)(2))^(2)=-\frac(3)(2)$ voor alle x(omdat $|\cos (x)|\leq 1$);
$f(\frac(\pi)(3))= \frac(3)(4)-(\cos(\frac(\pi)(3))-\frac(1)(2))^(2 )=\frac(3)(4)$;
$f(\pi)= \frac(3)(4)-(\cos(\pi)-\frac(1)(2))^(2)=-\frac(3)(2)$;
Antwoord: $\frac(3)(4)$ en $-\frac(3)(2)$
Als je dit probleem oplost met behulp van afgeleiden, moet je de obstakels overwinnen die samenhangen met het feit dat de functie f (x) niet op een segment, maar op de hele reële lijn is gedefinieerd.
De methode van grenzen/schattingen gebruiken
Uit de definitie van sinus volgt dat $-1\leq\sin(x)\leq 1$. Vervolgens gebruiken we de eigenschappen van numerieke ongelijkheden.
$-4\leq - 4\sin(x)\leq 4$, (vermenigvuldig alle drie de delen van de dubbele ongelijkheid met -4);
$1\leq 5 - 4\sin(x)\leq 9$ (toegevoegd aan de drie delen van de dubbele ongelijkheid 5);
Aangezien deze functie continu is over het hele definitiedomein, ligt de set van zijn waarden tussen de kleinste en grootste waarde over het hele definitiedomein, indien aanwezig.
In dit geval is de verzameling waarden van de functie $y = 5 - 4\sin(x)$ de verzameling.
Uit de ongelijkheden $$ \\ -1\leq\cos(7x)\leq 1 \\ -5\leq 5\cos(x)\leq 5 $$ verkrijgen we de schatting $$\\ -6\leq y\ lek 6$ $
Voor x = p en x = 0 heeft de functie de waarden -6 en 6, d.w.z. bereikt de onder- en bovengrenzen. Als lineaire combinatie van cos(7x) en cos(x) continue functies is de y-functie continu langs de gehele getallenas, dus door de eigenschap van een continue functie neemt het alle waarden van -6 tot en met 6, en alleen zij, omdat vanwege de ongelijkheden $- 6\leq y\leq 6$ andere waarden er onmogelijk voor zijn.
Daarom is E(y) = [-6;6].
$$ \\ -1\leq\sin(x)\leq 1 \\ 0\leq\sin^(2)(x)\leq 1 \\ 0\leq2\sin^(2)(x)\leq 2 \\ 1\leq1+2\sin^(2)(x)\leq 3 $$ Antwoord: E(f) = .
$$ \\ -\infty< {\rm tg}\, x < +\infty \\ 0 \leq {\rm tg}^{2}\, x < +\infty \\ 3 \leq 3+{\rm tg}^{2}\, x < +\infty \\ 2^{3} \leq 2^{3+{\rm tg}^{2}\, x} < +\infty \\ -\infty < -2^{3+{\rm tg}^{2}\, x} \leq -8 \\ -\infty < 3-2^{3+{\rm tg}^{2}\, x} \leq -5 $$ Ответ: E(f) = (–∞; -5].
$$ \\ -\infty< \lg{x} < +\infty \\ 0 \leq \lg^{2}{x} < +\infty \\ -\infty < -\lg^{2}{x} \leq 0 \\ -\infty < 16-\lg^{2}{x} \leq 16 \\ 0 \leq \sqrt{16-\lg^{2}{x}} \leq 4 \\ 2 \leq 2+\sqrt{16-\lg^{2}{x}} \leq 6 $$ Ответ: E(f) = .
Laten we de uitdrukking $$ \\ \sin(x) + \cos(x) = \sin(x) + \sin(\frac(\pi)(2) - x) = \\ 2\sin\left transformeren ((\ frac(x + \frac(\pi)(2) - x)(2)) \right)\cos\left ((\frac(x + \frac(\pi)(2) + x)( 2)) \right) \\ = 2\sin(\frac(\pi)(4))cos(x +\frac(\pi)(4)) = \sqrt(2)cos(x +\frac( \pi) (4)) $$.
De definitie van cosinus impliceert $$ \\ -1\leq\cos(x)\leq 1; \\ -1\leq \cos((x + \frac(\pi)(4)))\leq 1; \\ -\sqrt(2)\leq \sqrt(2)\cos((x +\frac(\pi)(4)))\leq\sqrt(2); $$
Aangezien deze functie continu is op het hele definitiedomein, is de verzameling van zijn waarden ingesloten tussen zijn kleinste en grootste waarde, indien aanwezig, de reeks waarden van de functie $y =\sqrt(2)\ cos((x +\frac(\pi)(4 )))$ is de set $[-\sqrt(2);\sqrt(2)]$.
$$\\ E(3^(x)) = (0;+∞), \\ E(3^(x)+ 1) = (1;+∞), \\ E(-(3^(x )+ 1)^(2) = (-∞;-1), \\ E(5 – (3^(x)+1)^(2)) = (-∞;4) $$
Geef $t = 5 – (3^(x)+1)^(2)$ aan, waarbij -∞≤t≤4. Het probleem wordt dus teruggebracht tot het vinden van de reeks waarden van de functie $y = \log_(0,5)(t)$ op de straal (-∞;4). Aangezien de functie $y = \log_(0,5)(t)$ alleen is gedefinieerd voor t > 0 , valt de reeks waarden op de straal (-∞;4) samen met de reeks waarden van de functie op het interval (0;4) dat het snijpunt is van de straal (-∞;4) met het definitiedomein (0;+∞) van de logaritmische functie. Op het interval (0;4) is deze functie continu en afnemend. Voor t > 0 neigt het naar +∞, en voor t = 4 neemt het de waarde -2 aan, dus E(y) = (-2, +∞).
We gebruiken een techniek die gebaseerd is op een grafische weergave van een functie.
Na transformaties van de functie hebben we: y 2 + x 2 = 25, en y ≥ 0, |x| 5.
Er moet aan worden herinnerd dat $x^(2)+y^(2)=r^(2)$ de vergelijking is van een cirkel met straal r.
Onder deze beperkingen is de grafiek van deze vergelijking de bovenste halve cirkel gecentreerd op de oorsprong en de straal gelijk aan 5. Het is duidelijk dat E(y) = .
Antwoord: E(y) = .
Referenties
De reikwijdte van functies in de taken van het Unified State Examination, Minyuk Irina Borisovna
Tips voor het vinden van de set functiewaarden, Belyaeva I., Fedorova S.
De set functiewaarden vinden
Hoe problemen in wiskunde op te lossen bij toelatingsexamens, I.I. Melnikov, I.N. Sergeev
GBOU lyceum (economisch) met. Isakla

Docent wiskunde Kuzaeva V.N.
2016
Referentiematerialen
Oplossing Voorbeeld: Zoek set functiewaarden

Functiebereik:  is
is
ja - elk nummer
Functiebereik:  is
ja
- elk nummer
is
ja
- elk nummer



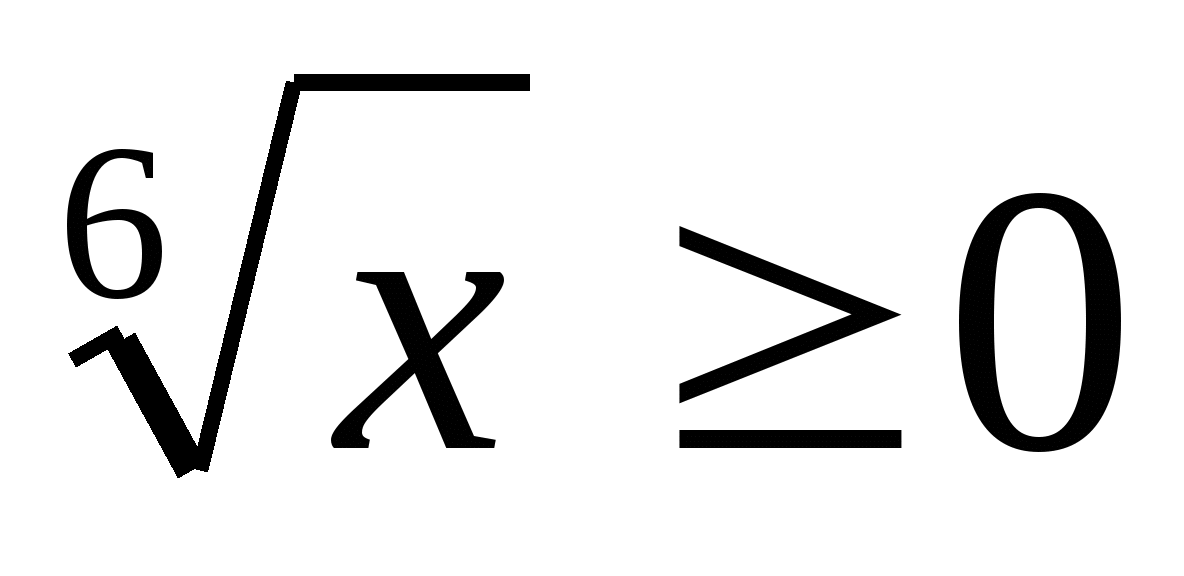
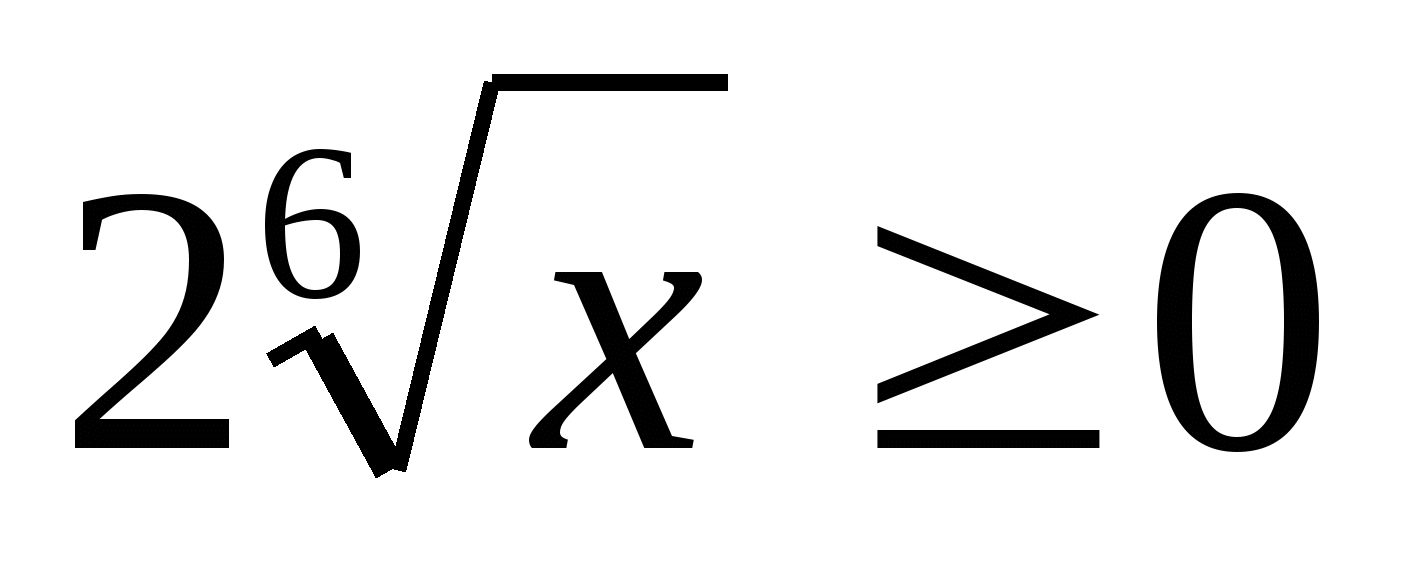

Veel waarden

ja - elk nummer


Hoogste waarde
Laagste waarde



Domein X
- elk nummer  , waar
, waar 
 , waar
, waar 
Veel waarden  ja
- elk nummerja
- elk nummer
ja
- elk nummerja
- elk nummer
Sjablonen plotten voor sommige trigonometrische functies
Reeks waarden van trigonometrische functies
Optie 1
Y =zonde 3x+2.
1) (-5;5) 2) 3) 4) (1;5)
2. Zoek het gebied van de functie y =tg x + 1.
1) 3) (-∞;∞) 4)

1) -6 2) 6 3) -4 4) -2
4. Specificeer het kleinste gehele getal uit het bereik van de functie
y = 12,7 + 5 zonde(3x-2).
1) -5 2) 8 3) 5 4) 17
5. Specificeer de functie waarvan de reeks waarden het segment [-2;2] is.
1) y = omdat 2x 2) y = zonde 2 x 3) ja = omdat 2 x +2
4) ja = 2 zonde 4 x
6. Zoek de set functiewaardenja =
tg 2
xop het segment 



7. Vind de som van alle gehele getallen die binnen het bereik van de functie vallenja = 4 omdat 2 x – 7.
1) -25 2) 25 3) -22 4) 0
Optie 2
ja = 2 omdat 5 x +3.
1) (2;3) 2) 3) (1;5) 4) .
2. Zoek het bereik van de functie 
1) 3) (-∞;∞) 4) .
3. Specificeer het kleinste getal uit het bereik van de functie

1) 4 2) -3 3) 1 4) -7
4. Specificeer het grootste gehele getal uit het bereik van de functie

1) 2 2) 13 3) 12 4) -2
5. Specificeer een functie waarvan de reeks waarden het segment [-5;5] is.
1) y = zonde 5x 2) y = 5 cos 5x 3) y = cos (-5x)
4) y = zonde 5x + 5
6. Zoek de set functiewaarden  op het segment
op het segment 




7. Zoek het product van alle gehele getallen binnen het bereik van de functie y \u003d 5 - 3zonde 2 x.
1) 120 2) 14 3) -15 4) 0
Optie 3
1. Specificeer een set functiewaardenja =
zonde 3
x + 5.
1) (-4;6) 2) 3) [-1;5) 4) (0;6)

1) 2) (0;3) 3) (1;3) 4) [-1;3)
3. Specificeer het kleinste getal uit het bereik van de functie y = 5tg 2 x+2?
1) 5 2) 0 3) 7 4) 2

1) -1 2) -2,7 3) -2,3 4)-3
5. Specificeer een functie waarvan de reeks waarden een segment is
[-17;-13].
1) y \u003d 5 sin x - 8 3) y \u003d -cos x +15
2) y = 2 cos x - 15 4) y = 3 sin x +10
6. Geef het kleinste natuurlijke getal aan dat niet is opgenomen in de set functiewaarden 
1) 2 2) 4 3) 15 4) 6
7. Hoeveel gehele getallen behoren tot de set functiewaarden
ja = 2 omdat 3 x +10?
1) 2 2) 3 3) 4 5) 5
Optie 4

1) 2) 4) (-7;-6)
2. Zoek het bereik van de functie 
1) (1;5) 2) 3) (4;6) 4) [-6;-4]
3. Specificeer het grootste getal uit het bereik van de functieja = -3 ctg 2 x+7.
1) 10 2) 4 3) 7 4) -3
4. Welke van de volgende getallen is niet opgenomen in de set functiewaarden? 
1) -6 2) -5 3) -10 4) -7
5. Geef een functie op waarvan de reeks waarden het interval is.



6. Specificeer het grootste negatieve gehele getal dat niet is opgenomen in het bereik van de functie 
1) -1 2) -25 3) -6 4) -2
7. Hoeveel gehele getallen behoren tot de set functiewaarden 
1) 11 2) 3 3) 5 4) 4
Optie 5
1. Specificeer de set functiewaarden y = 2 -zonde 5 x.
1) (2;5) 2) 3) (1;3) 4) [-3;7]
2. Zoek het bereik van de functie 
1) [-8;-6] 2) [-8;-6) 3) (-8;-6) 4)
3. Specificeer het kleinste gehele getal uit het bereik van de functie
ja = 3 + zonde 2 2 x.
1) 0 2) 1 3) 3 4) 4
4. Welke van de volgende getallen is opgenomen in de set functiewaarden? 
1) 128 2) 10,5 3) 3 4) -235
5. Specificeer de functie waarvan de reeks waarden het segment [-9;15] is.




6. Zoek de som van gehele getallen in de set functiewaarden 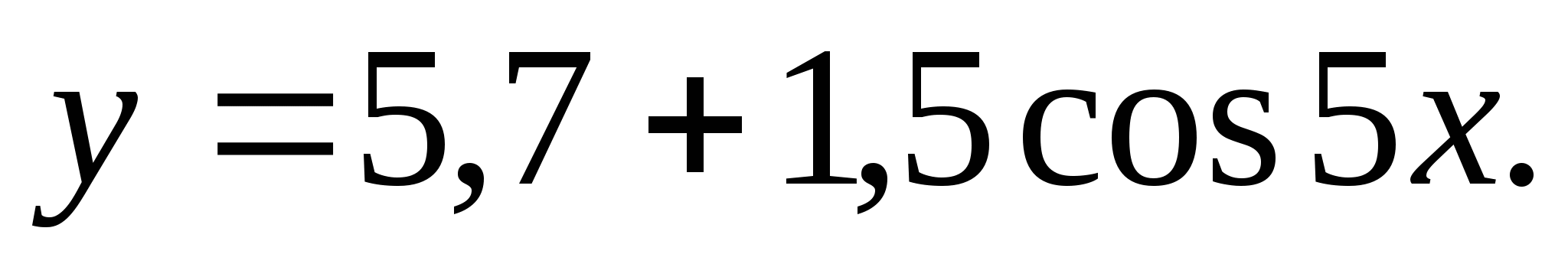
1) 0 2) 7 3) 18 4) 22
7. Vind de grootste waarde van een functie  op het segment
op het segment 
1) 0,5 2) 1,5 3) 0 4) 2
Optie 6
1. Specificeer het segment dat overeenkomt met de set functiewaarden 
1) 2) (-2;-1) 3) (0;1) 4) [-6;-4]
2. Zoek het bereik van de functie 
3. Specificeer het grootste getal uit het bereik van de functie 
1) 5 2) -6 3) -3 4) 4
4. Welke van de volgende getallen is opgenomen in de set functiewaarden? 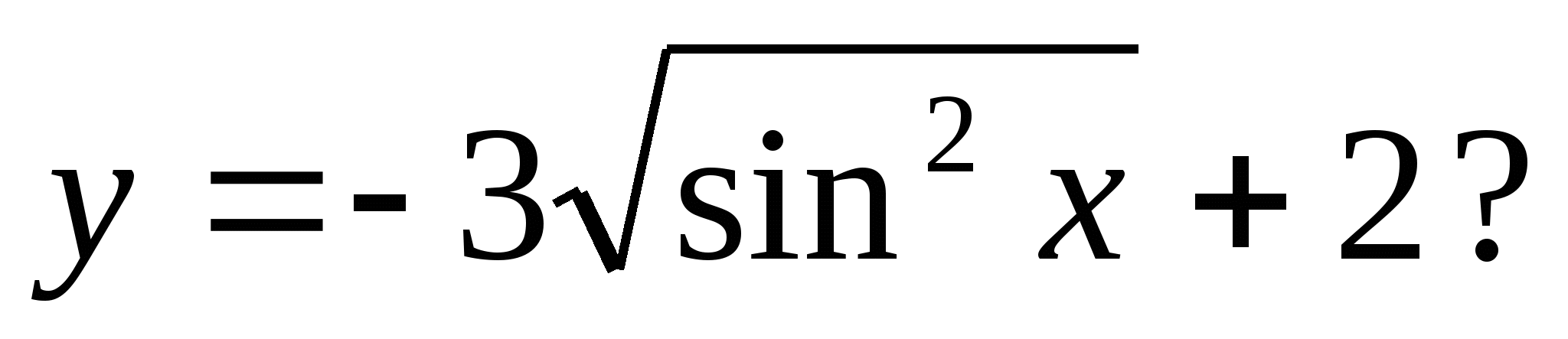
1) 5 2) 0 3) -3 4) 4
5. Geef een functie op waarvan de reeks waarden het interval is.
1) Bij = 15 – 7 cos 2x 3) y = 7 cos 2x + 3
2) ja = 5 omdat 4 x 4) ja = - tg 2 x + 1
6. Zoek het product van gehele getallen in de reeks waarden
ja = 3,8 – 1,4 zonde 3 x.
1) 17 2) 12 3) 0 4) 60
7. Zoek de set functiewaarden 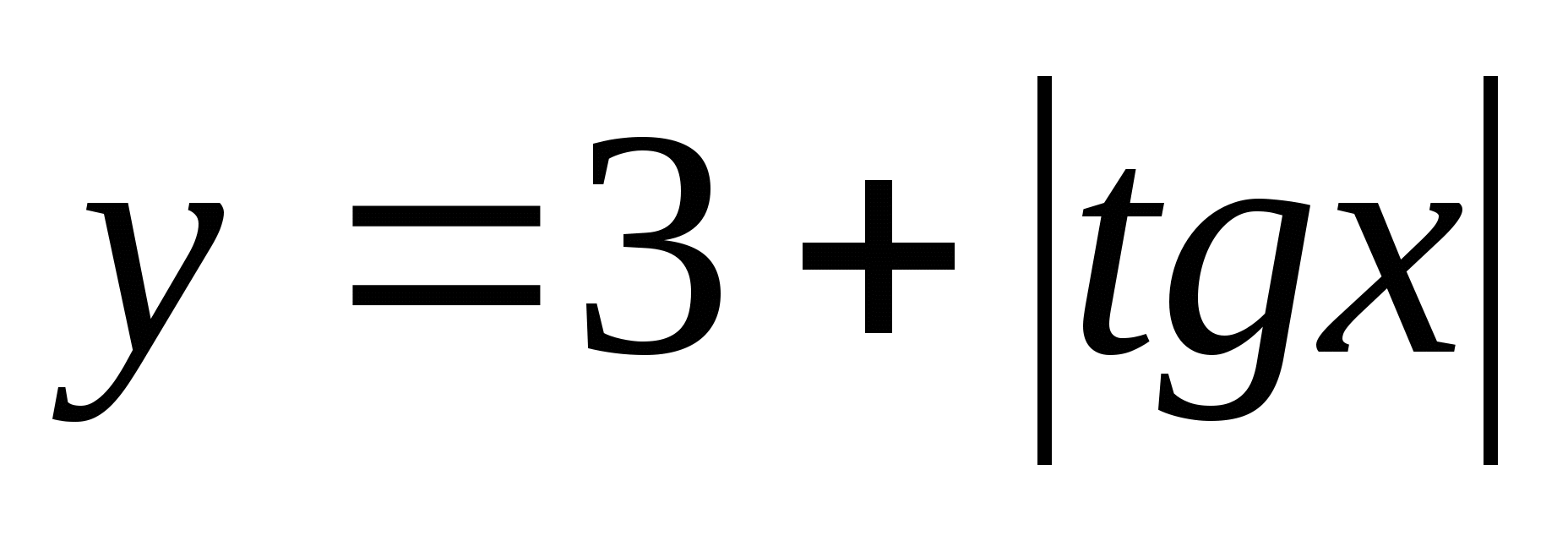 tussenin
tussenin 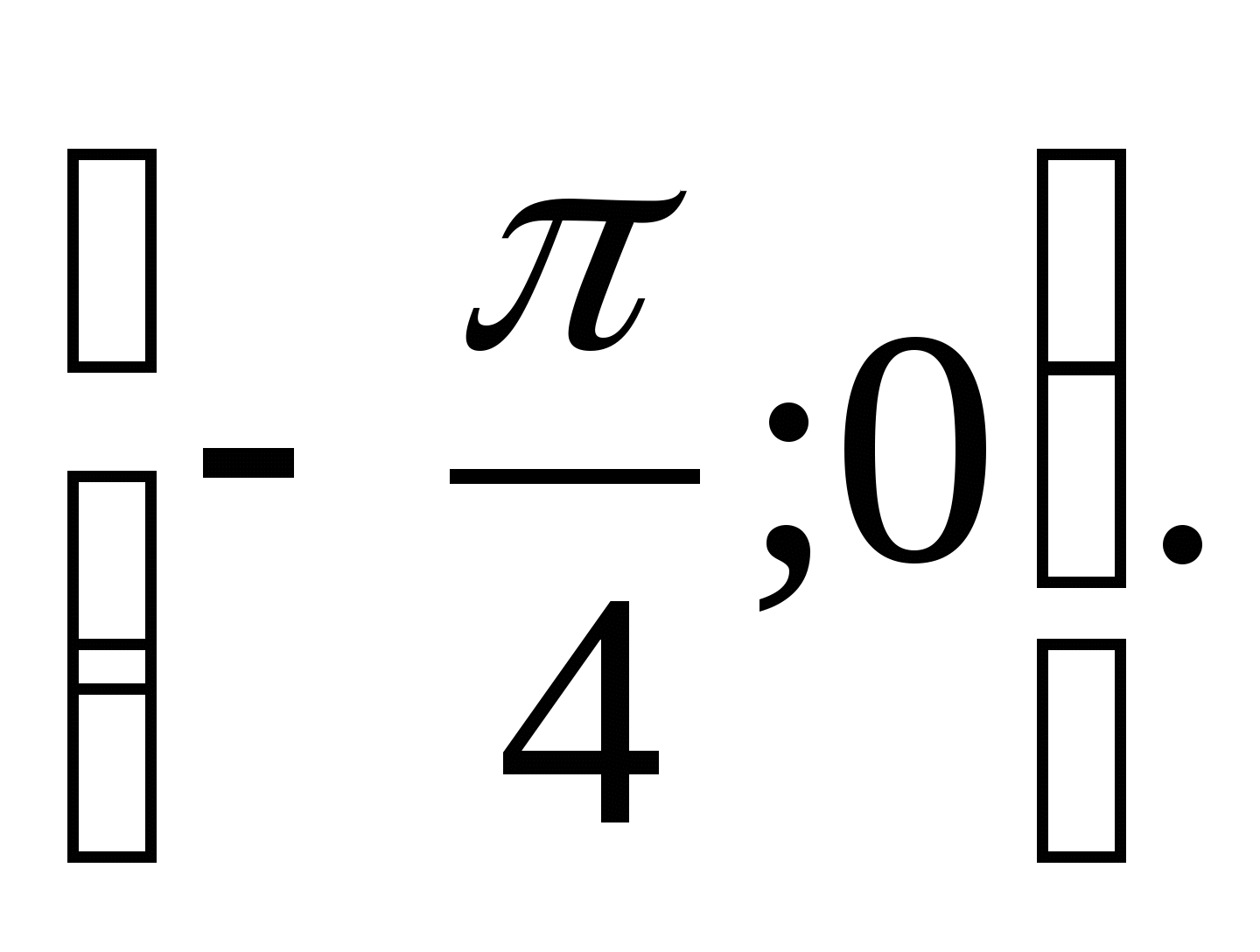
1) (3;4) 2) 3)
Optie 7


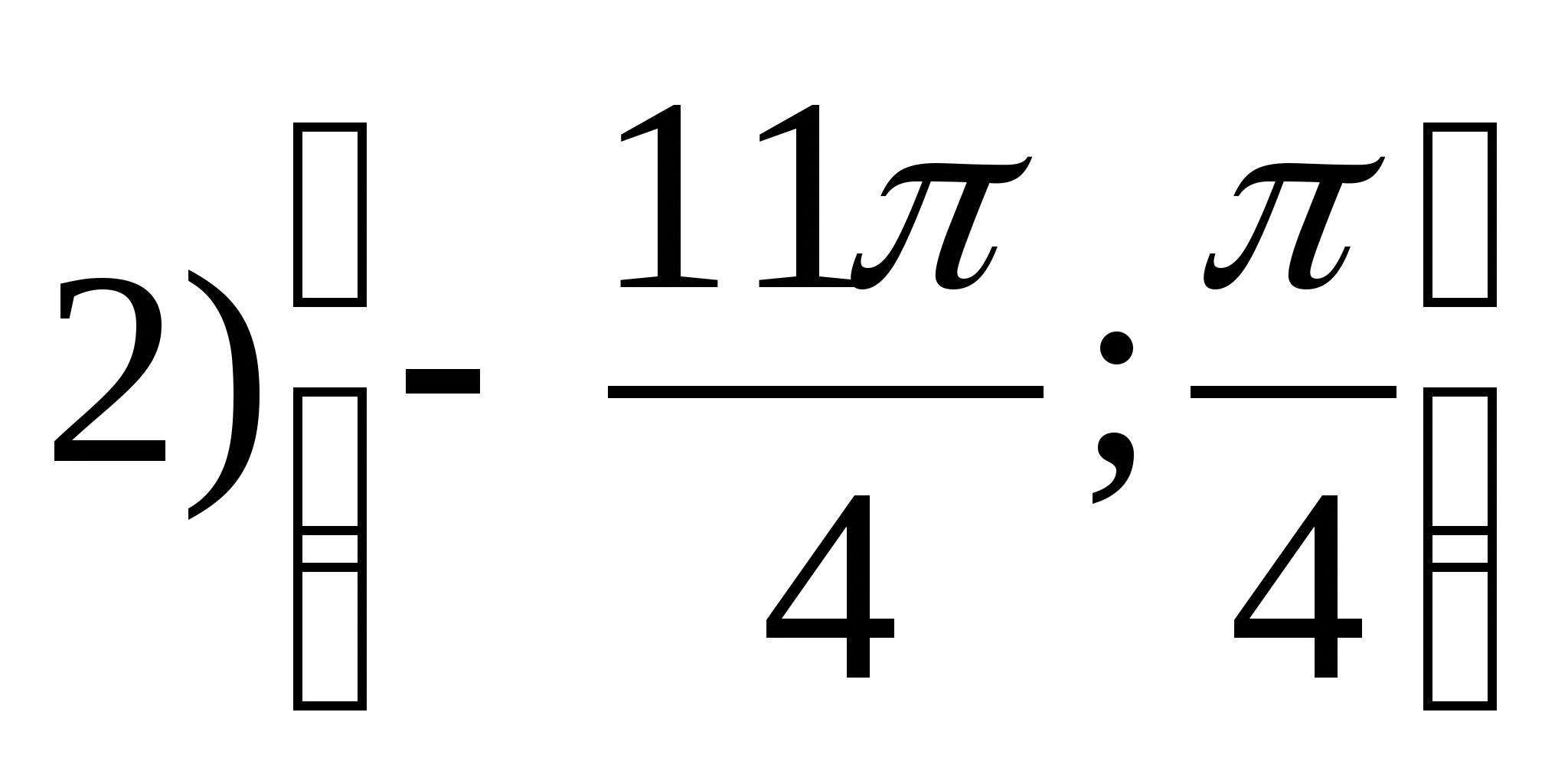
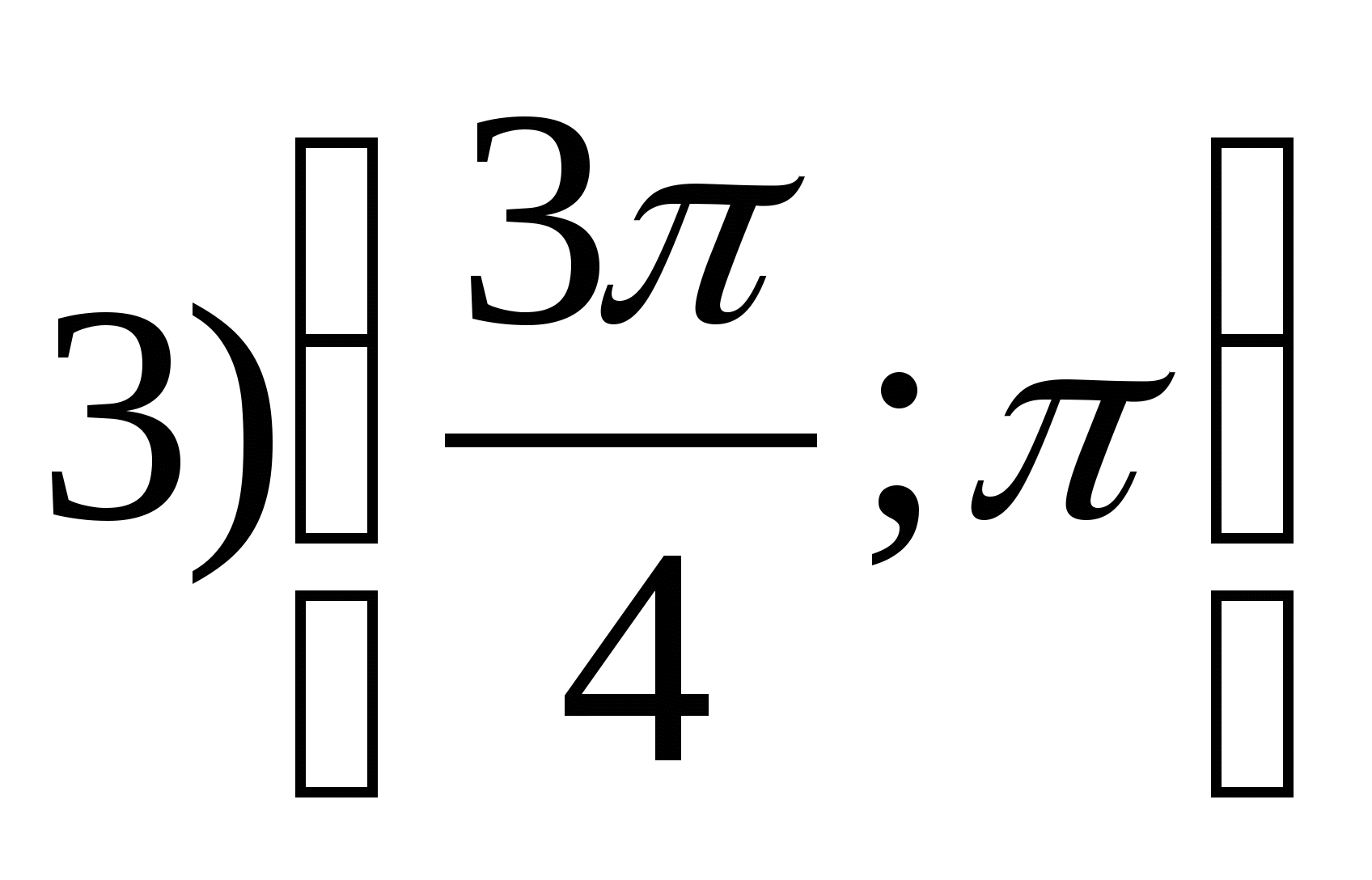

2. Vind de kleinste gehele waarde van de functie 
1) 2 2) 0 3) -3 4) -4

1) 0 2) 2 3) 4 4) 6
4. Voor welke waarden van a geldt de vergelijkingzonde(3 x-4)+5= a oplosbaar?
1) 2) 3) (4;6) 4) (-6;4]
zonde 2 2 x – 2.
1) [-3;-2] 2) [-1;0] 3) [-4;0] 4) [-3;-1]
 tussenin
tussenin 
 2) 0 3) 1
2) 0 3) 1
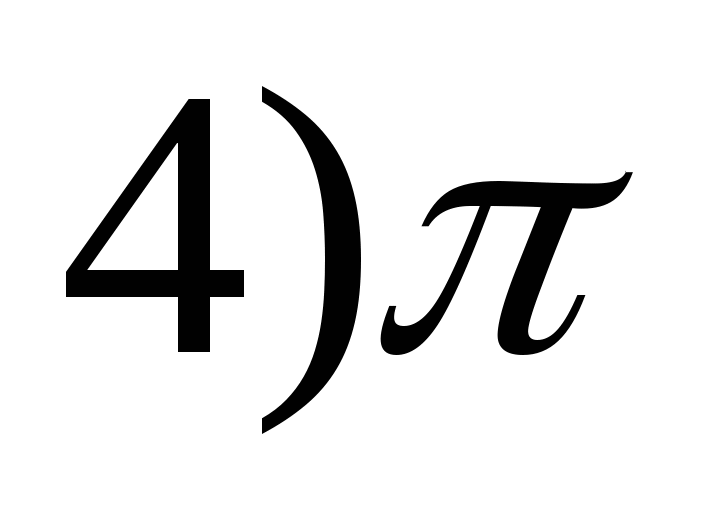
ja = 4 zonde(x 4 ) -2?
1) 8 2) 9 3) 7 4) 10
Optie 8
1. Zoek de set functiewaardenja = arctgx- 2π.
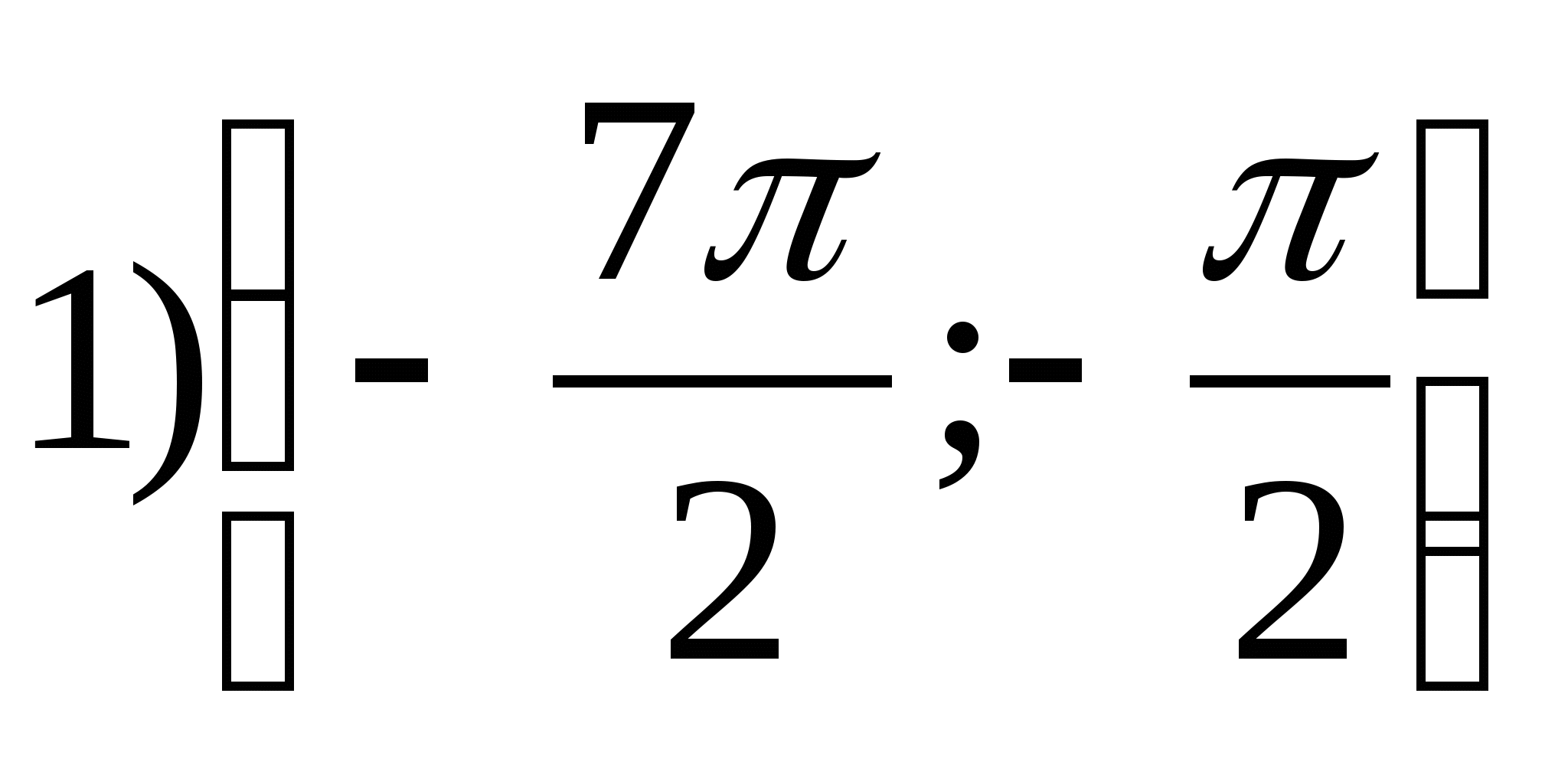
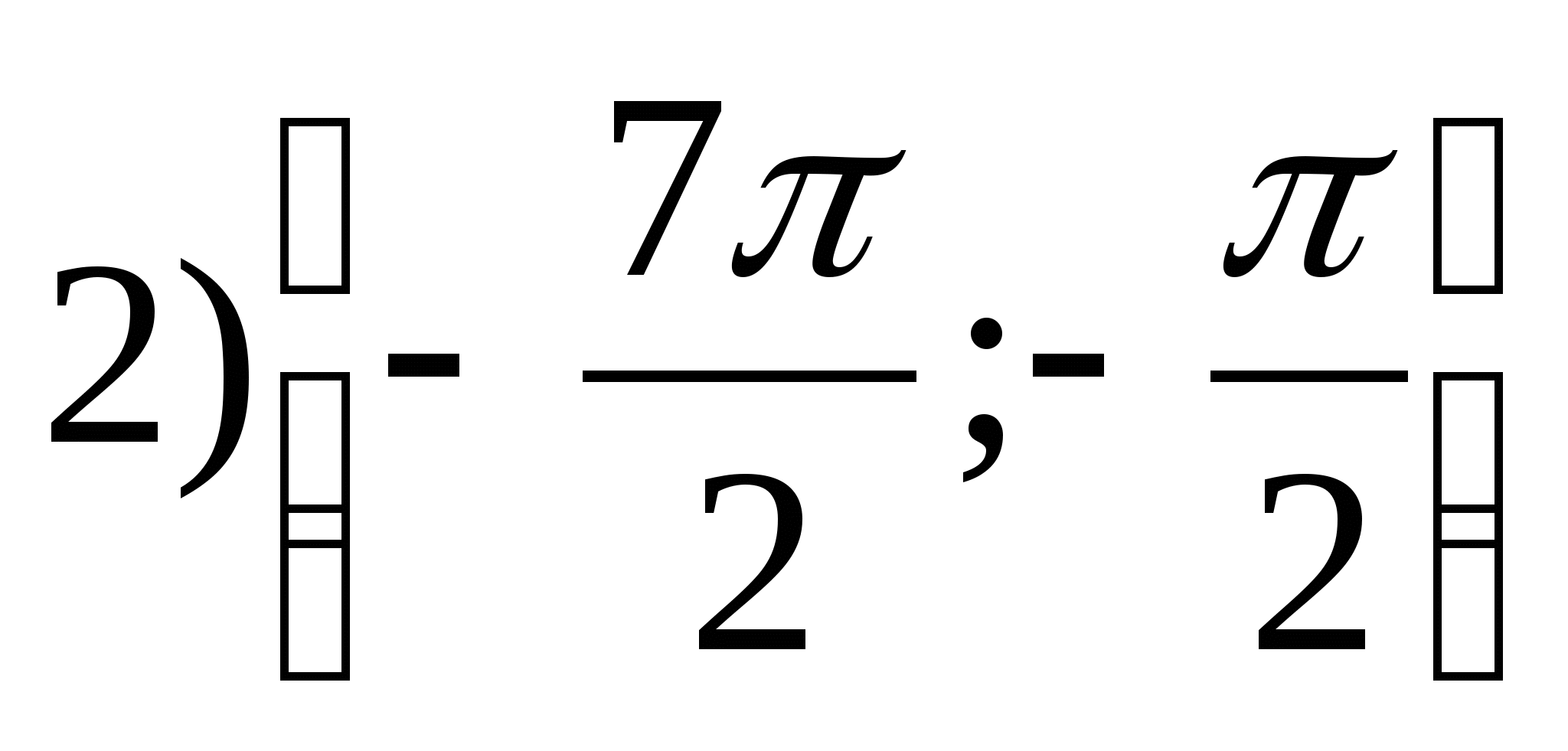

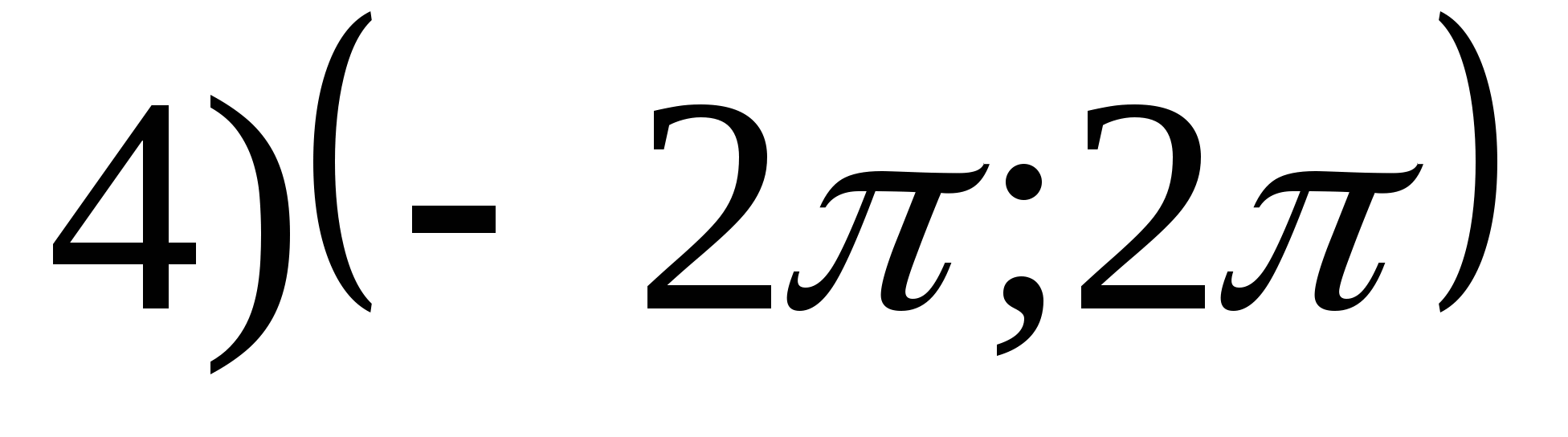
2. Vind de grootste waarde van de functie 
1) 1,75 2) 0 3) 2,25 4) -1,75
3. Welk van de volgende getallen kan de waarde van de functie zijn 
1) -4 2) -2 3) 0 4) 2
4. Voor welke waarden van p vergelijking -2+omdat(4 x-1)= p heeft wortels?
1) [-3;-1] 2) [-3;-1) 3) (-3;1] 4) (-3;-1)
5. Zoek de set functiewaardenja = -2 tg 2 x + 1.
1) [-1;3] 2) (-∞;1] 3) (-∞;∞) 4) [-1;+∞)
 tussenin
tussenin  .
.
1) 0 2) 1 3) -1 4) 3
7. Hoeveel gehele getallen zijn er in het bereik van de functie
1) 4 2) 3 3) 5 4) 2
Optie 9
1. Zoek het bereik van de functie 




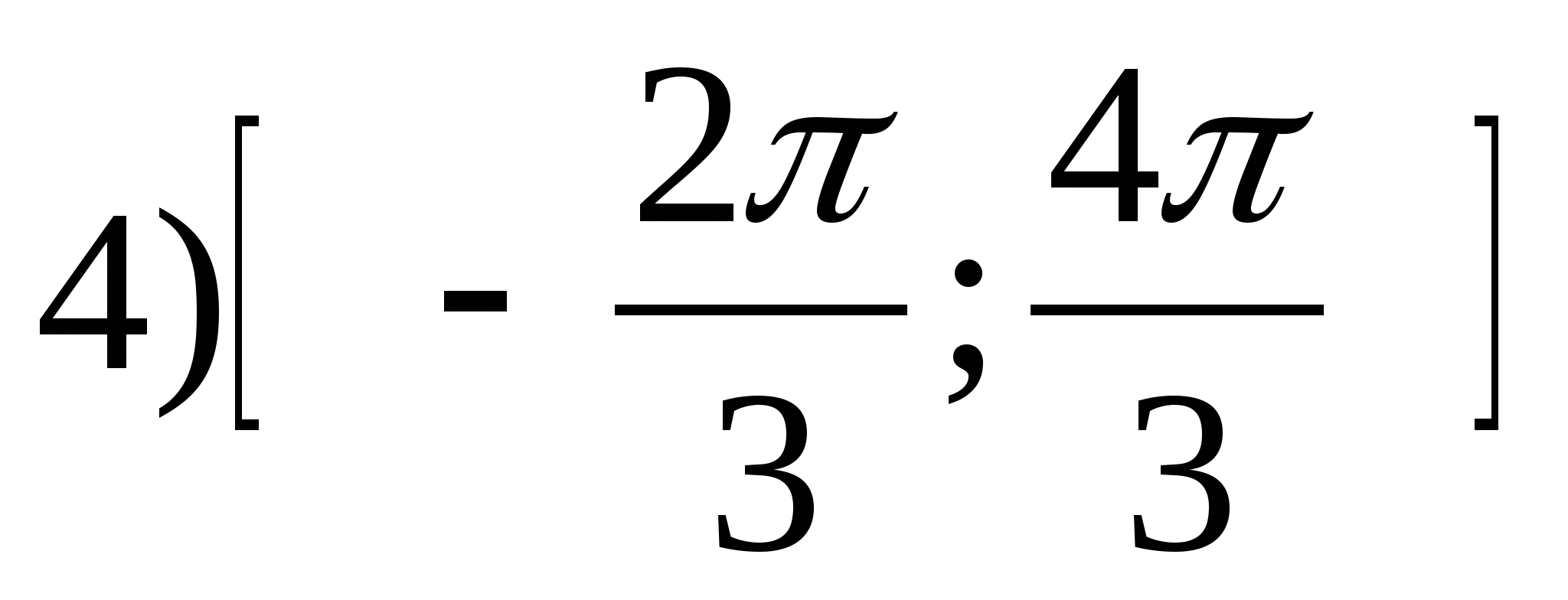
2. Vind de grootste gehele waarde van de functie 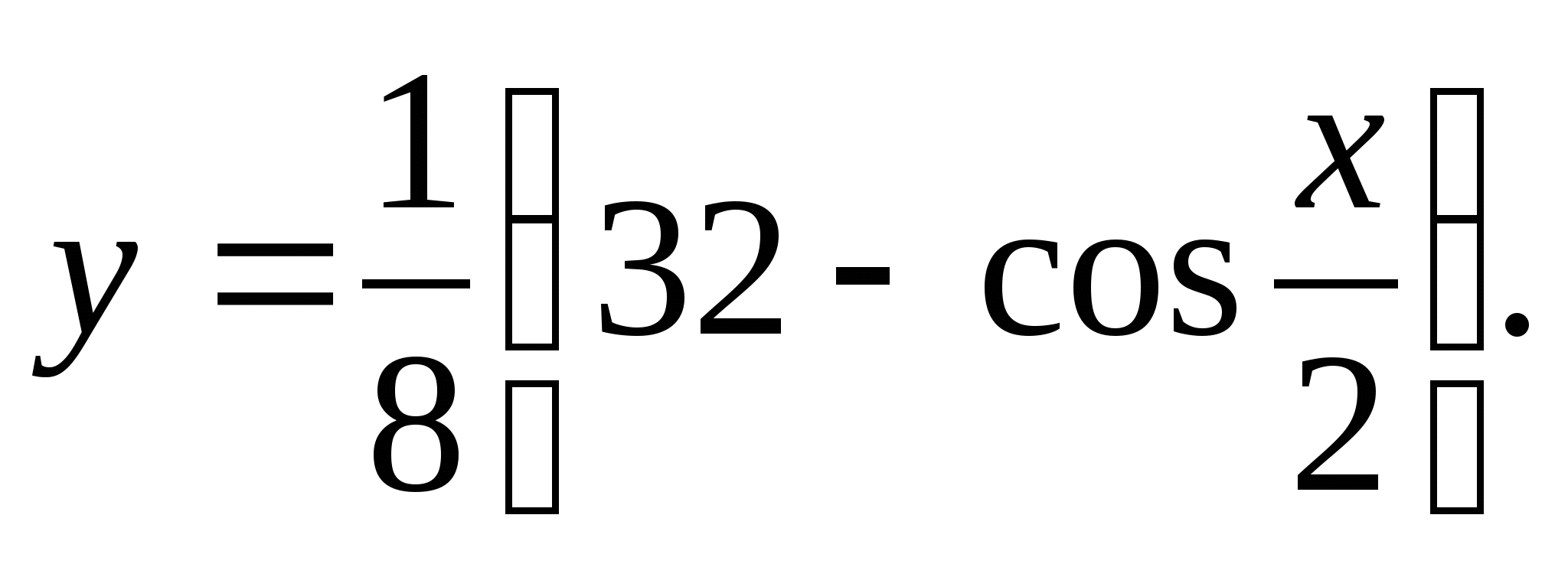
1) 4 2) 5 3) 6 4) 7
3. Welk van de volgende getallen kan de waarde van de functie zijn 
1) 0 2) 3 3) 6 4) 9
k de vergelijking - k + zonde(2 x-1) = 2 oplosbaar?
1) 2) (4;6) 3) (-3;-1) 4) [-3;-1]
5. Zoek de set functiewaarden \u200b\u200door \u003d -omdat 2 3 x + 4.
1) 2) 3) 4)
6. Specificeer de kleinste waarde van de functie  tussenin
tussenin 
 2) -1 3) 0 4) 1
2) -1 3) 0 4) 1
7. Zoek uit hoeveel gehele getallen er zijn in het bereik van de functie y = 12omdat 3 x +5 zonde 3 x.
1) 13 2) 27 3) 26 4) 14
Optie 10
1. Zoek het bereik van de functie 

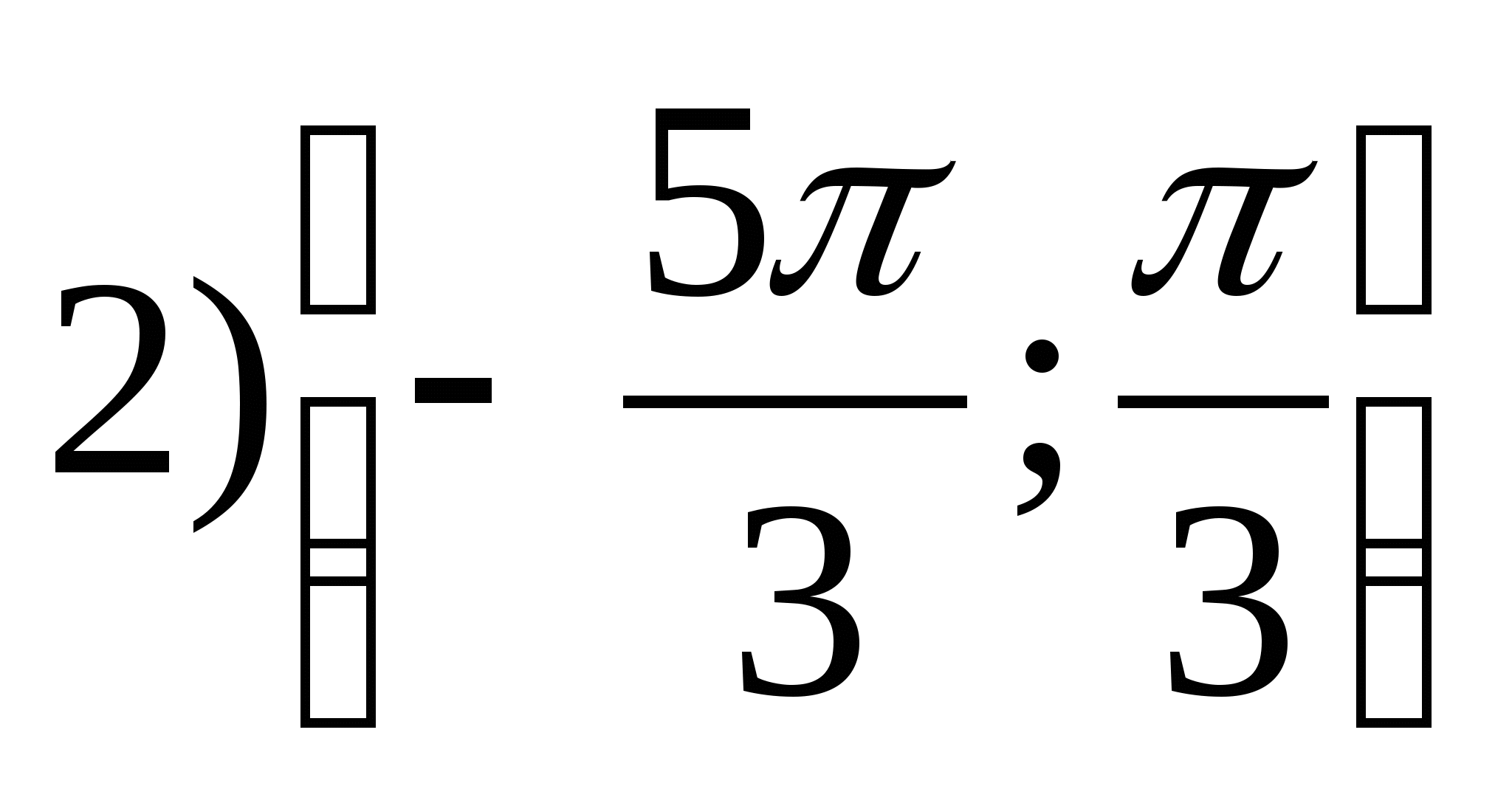

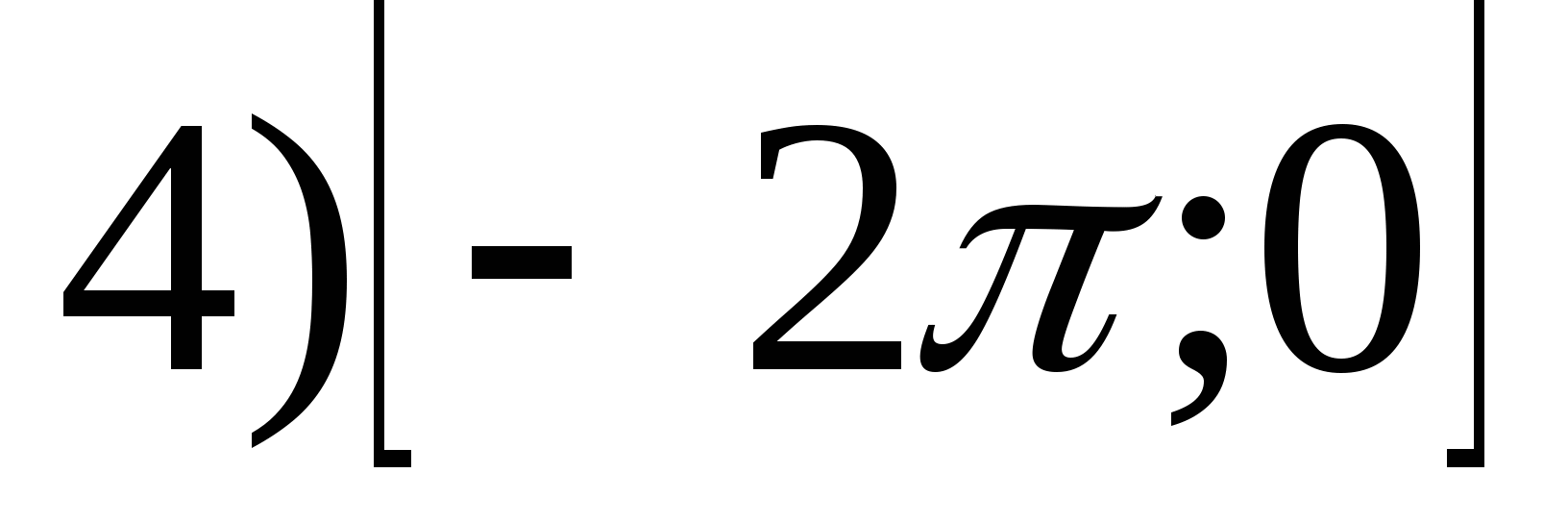
2. Vind de kleinste waarde van de functie 
1) 3,5 2) 0 3) 2,5 4) -3,5
3. Welk van de volgende getallen kan de waarde van de functie zijn 
1) -4 2) -1 3) 3 4) 7
4. Bij welke waarden van de parameterm de vergelijking omdat (3 x + 2)- m= 5 heeft wortels?
1) [-6;-4] 2) (-6;-4) 3) (-4;3) 4) [-6;-5]
5. Zoek de set functiewaarden \u200b\u200door \u003d -2ctg 2 3 x + 7.
1) (-∞;5] 2) (-∞;1] 3) (-∞;0] 4) (-∞;7]
6. Specificeer de grootste waarde van de functie  tussenin
tussenin 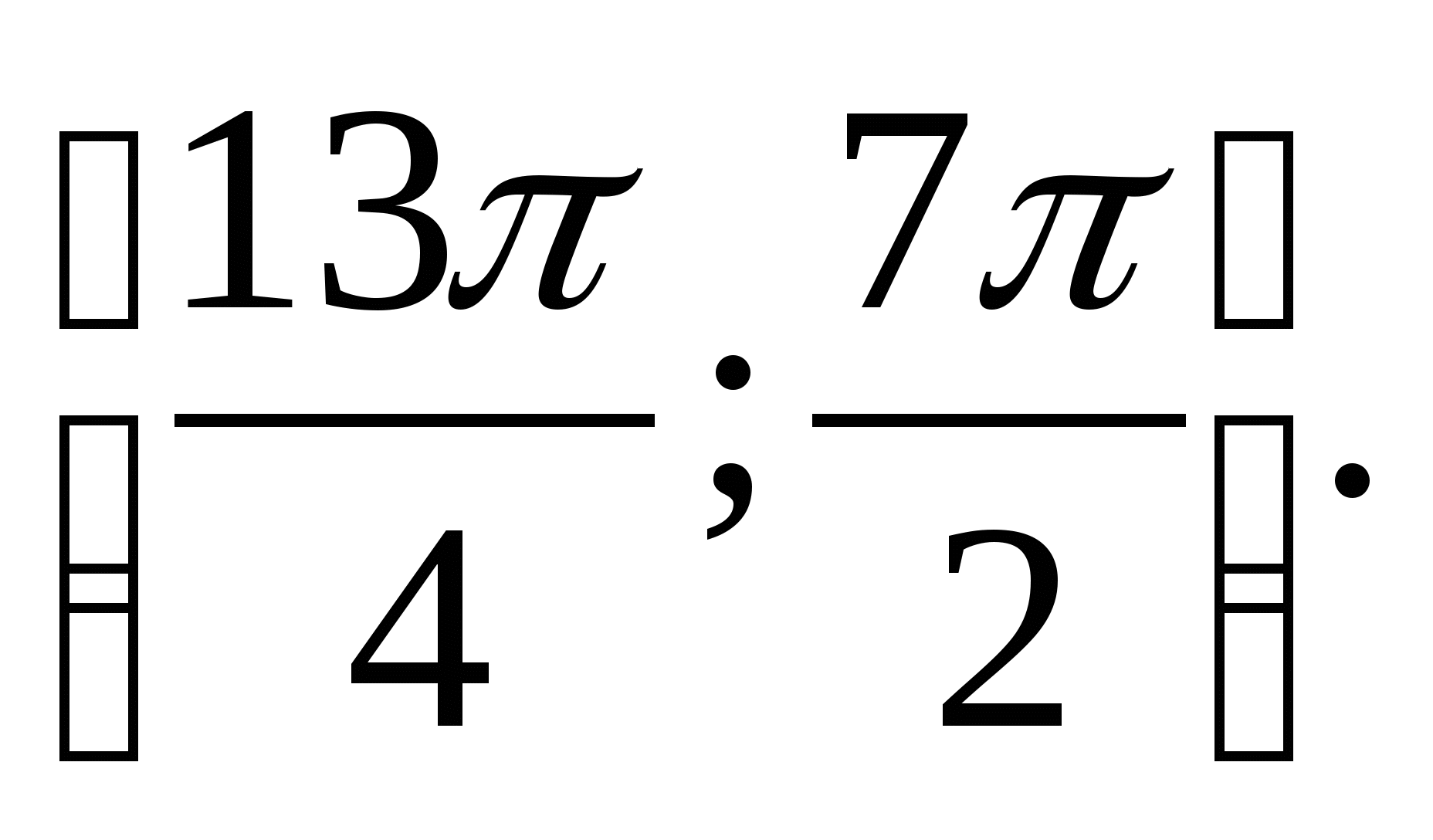
 2) 0 3) 2 4) 1
2) 0 3) 2 4) 1
7. Zoek uit hoeveel gehele getallen er in het bereik van de functie zitten 
1) 30 2) 35 3) 17 4) 7
Reeks waarden van exponentiële en logaritmische functies
Optie 1
1. Zoek het bereik van de functie 
1) 4) (-∞;3)
2. Specificeer een set functiewaarden 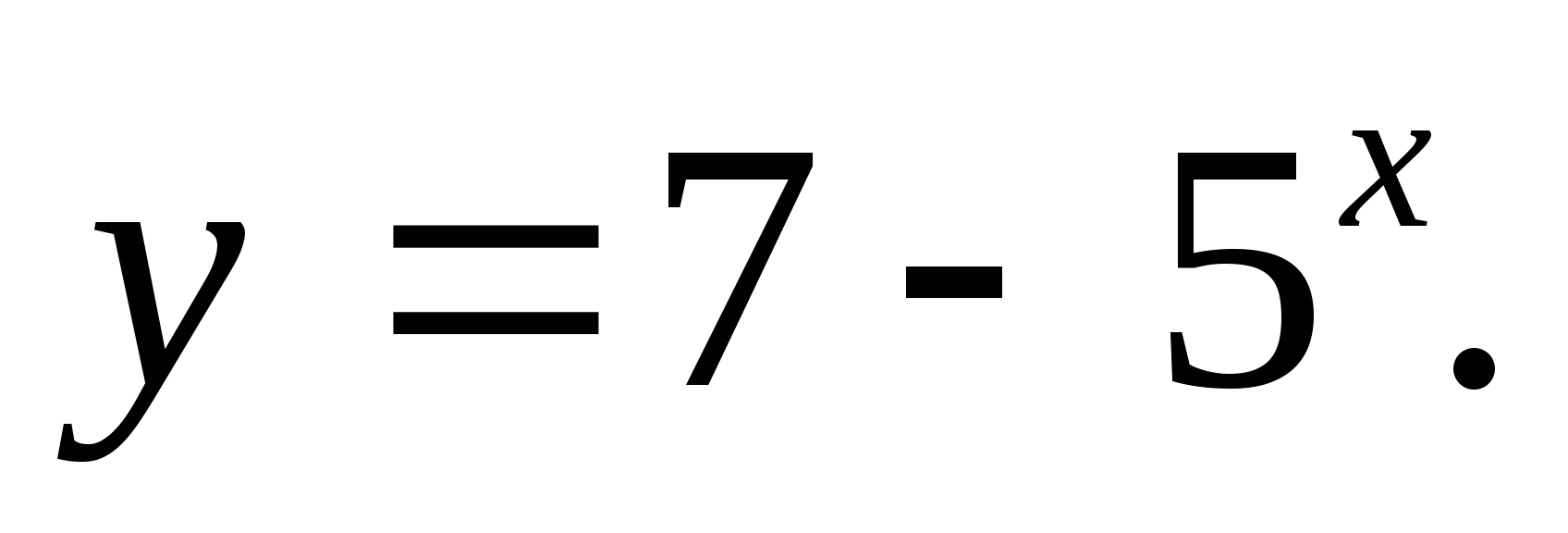
1) (-∞;7) 2) (-∞;-7) 3)(7;∞) 4) (-∞;7]

1) 0 2) 4 3) -3 4) -4

1) 15 2) 20 3) 43 4) 28
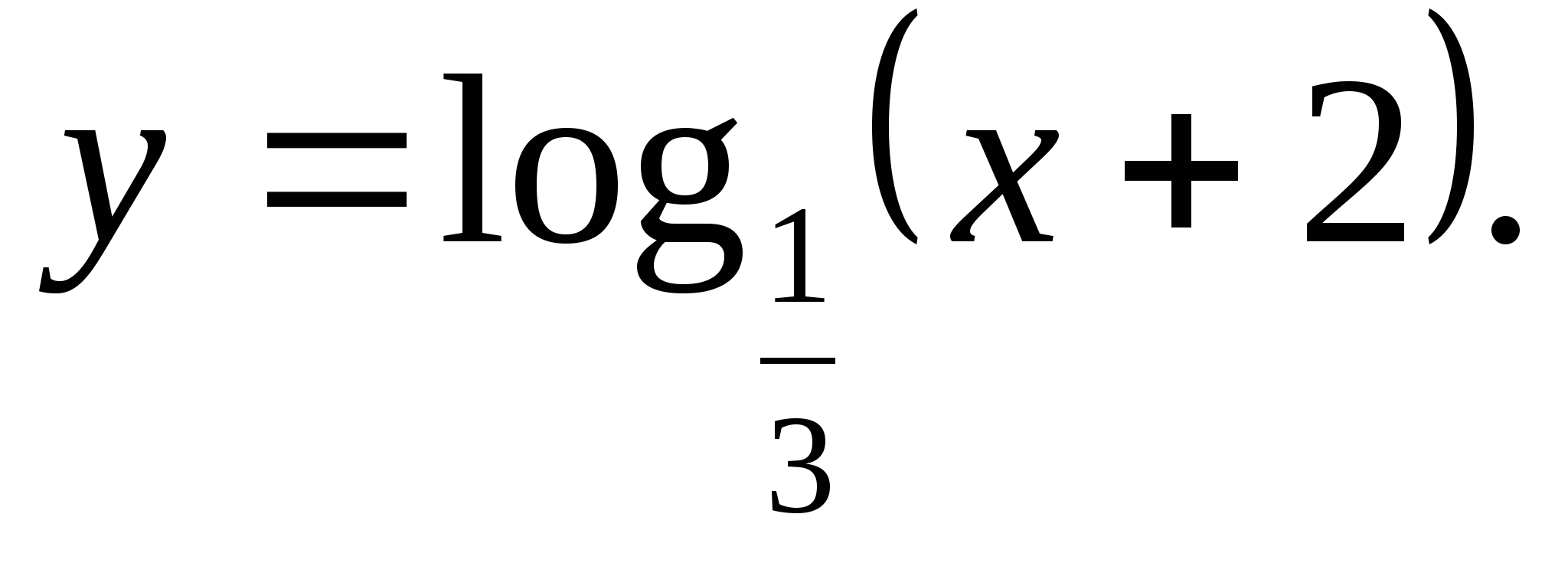
1) (0;-2) 2) (0;2) 3) (-∞;+∞) 4) [-2;0)
6. Specificeer de kleinste gehele waarde van de functie 
1) 1 2) -1 3) 0 4) -5
7. Specificeer een functie waarvan de reeks waarden het interval is (1;∞).
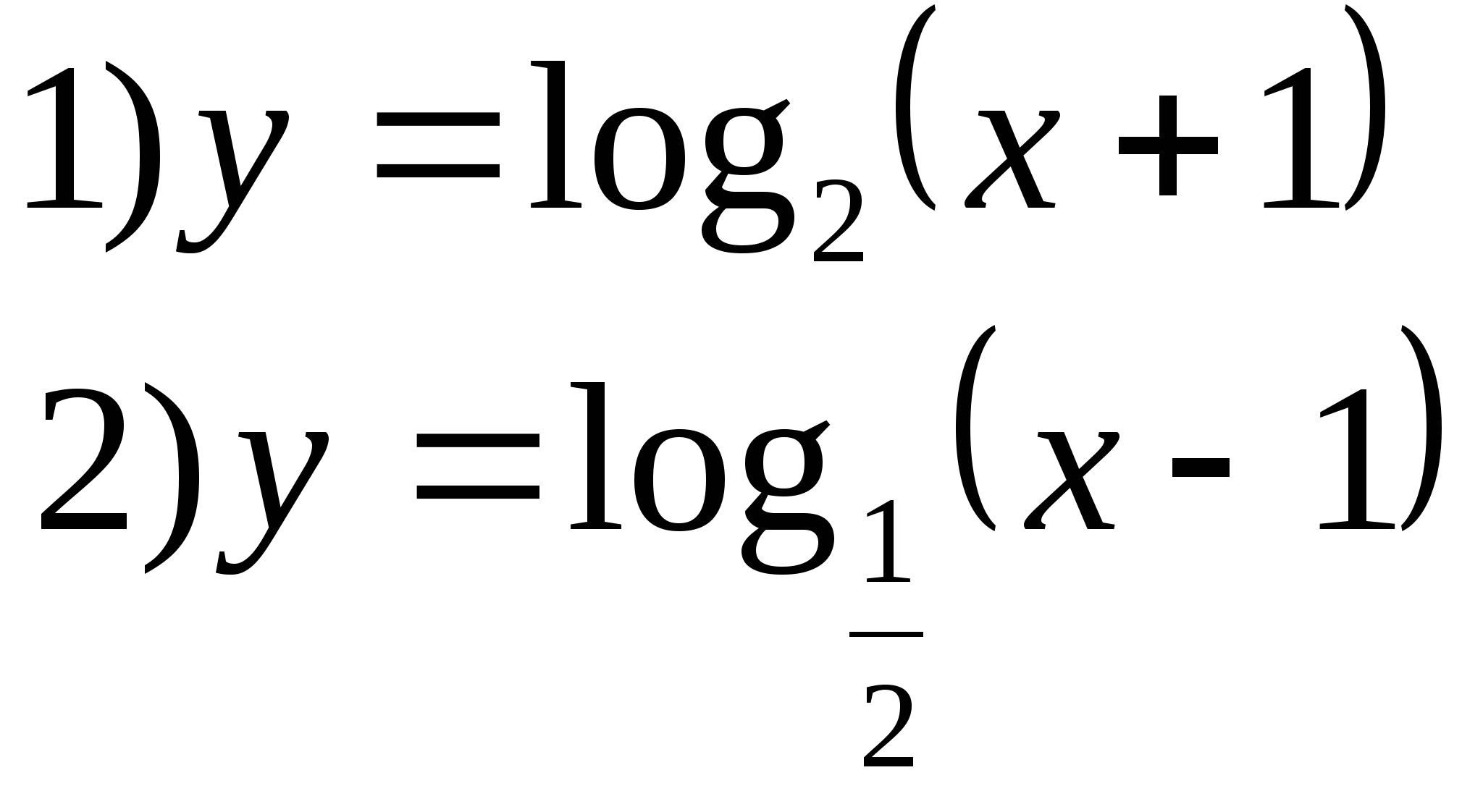

Optie 2
1. Specificeer een set functiewaarden 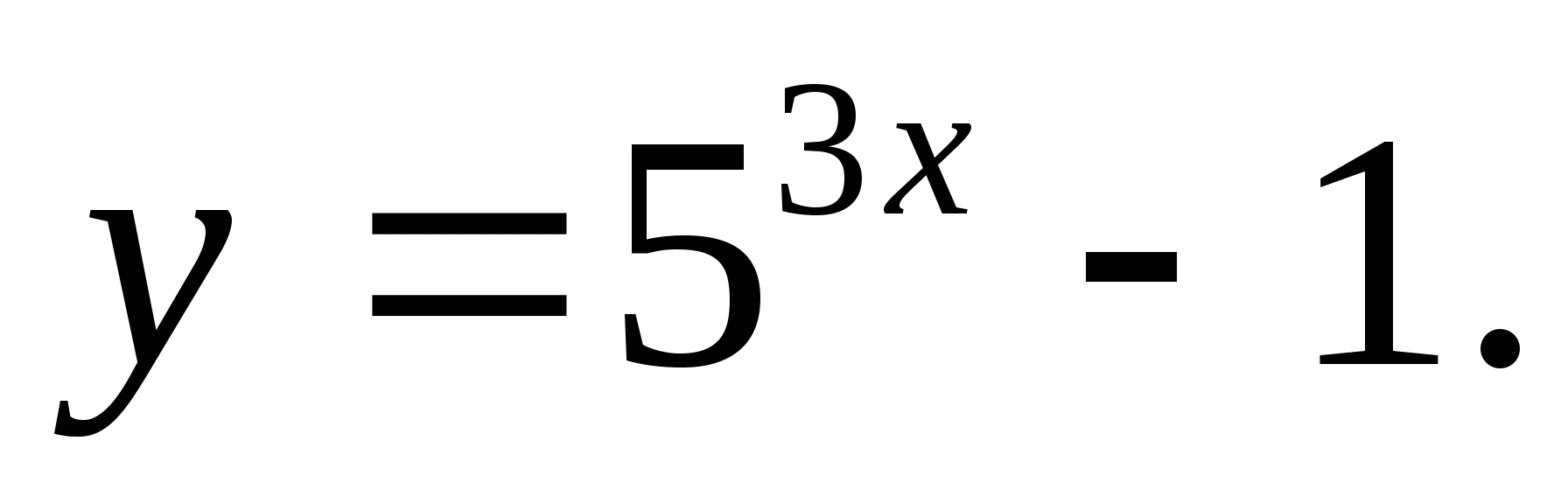
1) [-1;∞) 2)(-1;∞) 3) (3;∞) 4) 4) [-3;∞)
2. Zoek het bereik van de functie 
1) (-4;∞) 2) (4;∞) 3) (-∞;4] 4) 4) (-∞;4)
3. Specificeer de kleinste gehele waarde van de functie 
1) -12 2) -11 3) -10 4) -15
4. Geef een getal op dat niet bij de set functiewaarden hoort 
1) -42 2) 3 3) 1 4) -20
5. Specificeer een set functiewaarden 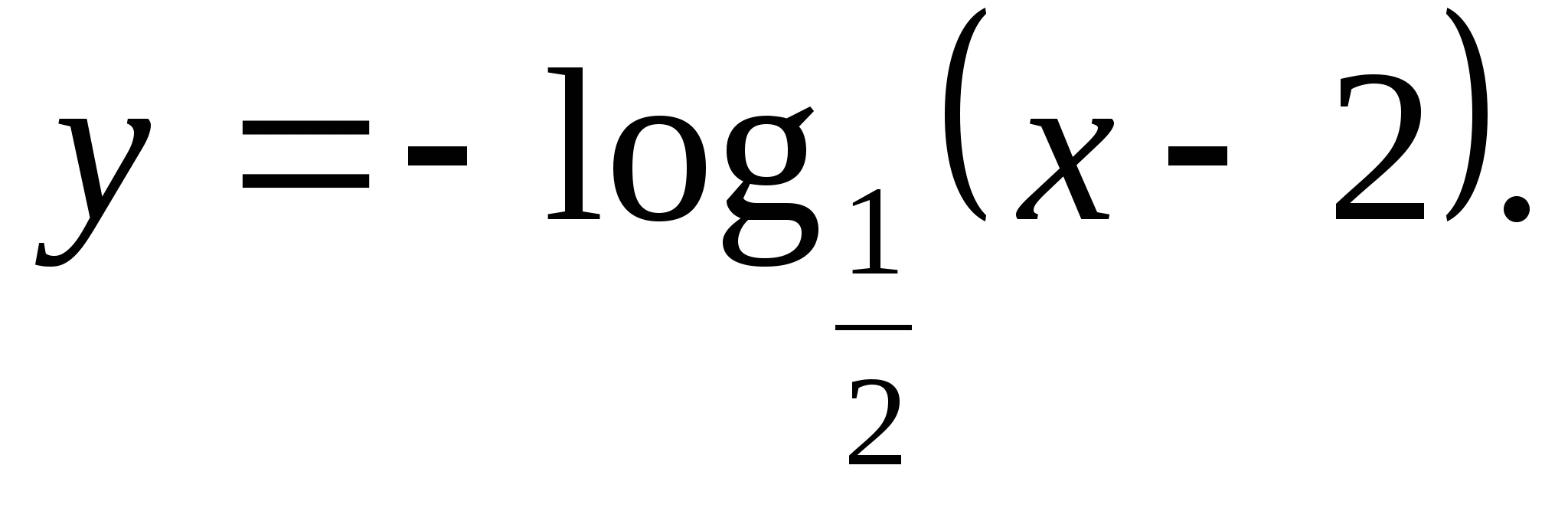
1) (-∞;0) 2) (0;∞) 3) (-∞;∞) 4) [-2;2]
6. Specificeer de grootste gehele waarde van de functie 
1) 10 2) 3 3) 9 4) 2
7. Specificeer een functie waarvan de reeks waarden het interval is
(-∞;13).


Optie 5
1. Specificeer de kleinste gehele waarde van de functie 
1) 0 2) -1 3) -2 4) -3
2. Welk van de volgende getallen valt binnen het bereik van de functie 
1) -3 2) -4 3) 5 4) 0
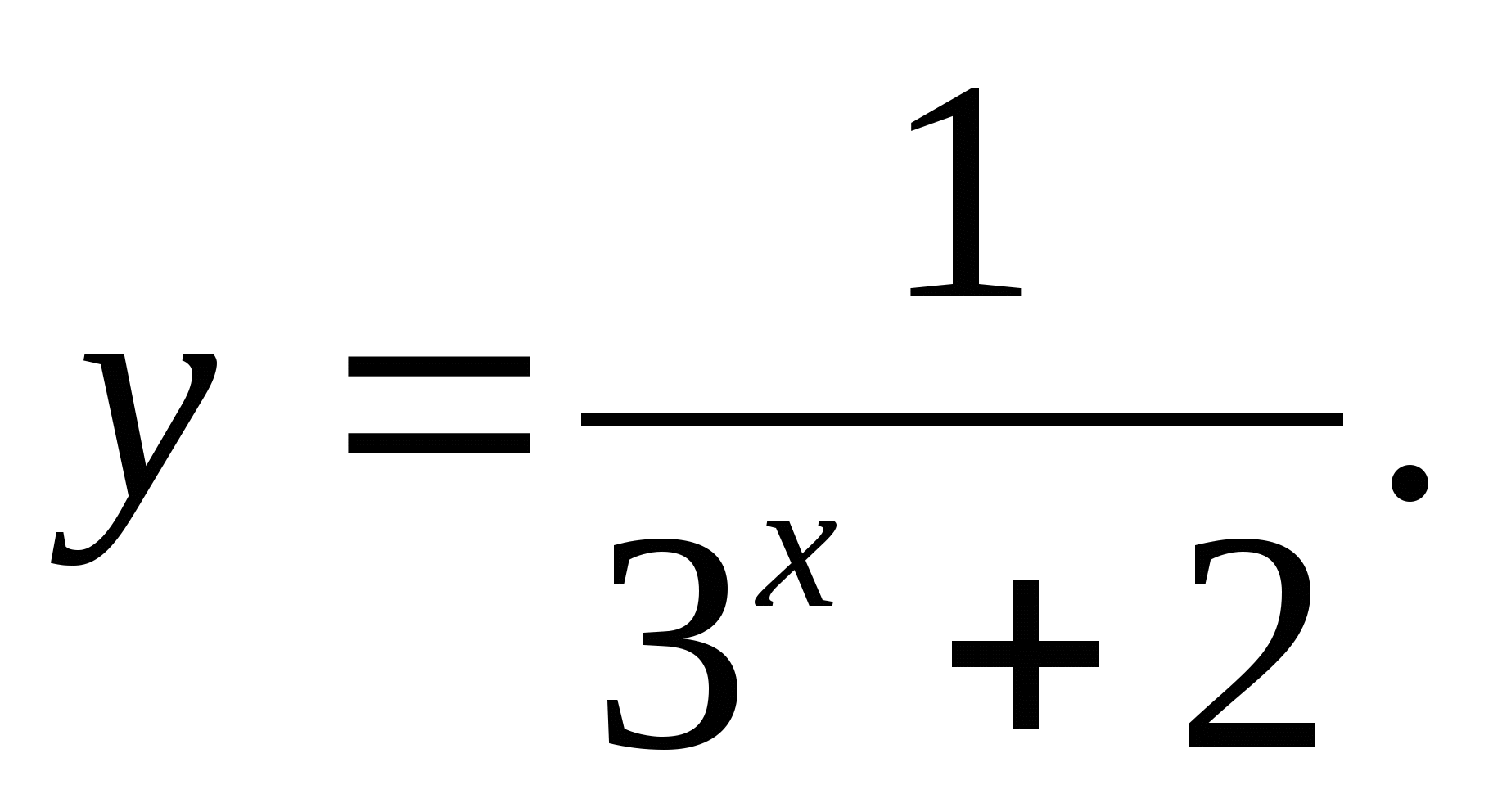
1) (-∞;2] 2) 2) [-1;1] 3) (-1;1) 4) (0;∞)
6. Zoek op welk segment de functie  neemt de grootste waarde van 2 en de kleinste waarde van -3 aan.
neemt de grootste waarde van 2 en de kleinste waarde van -3 aan.
1) 2) (-5;2) 3) 4) (-3;2)
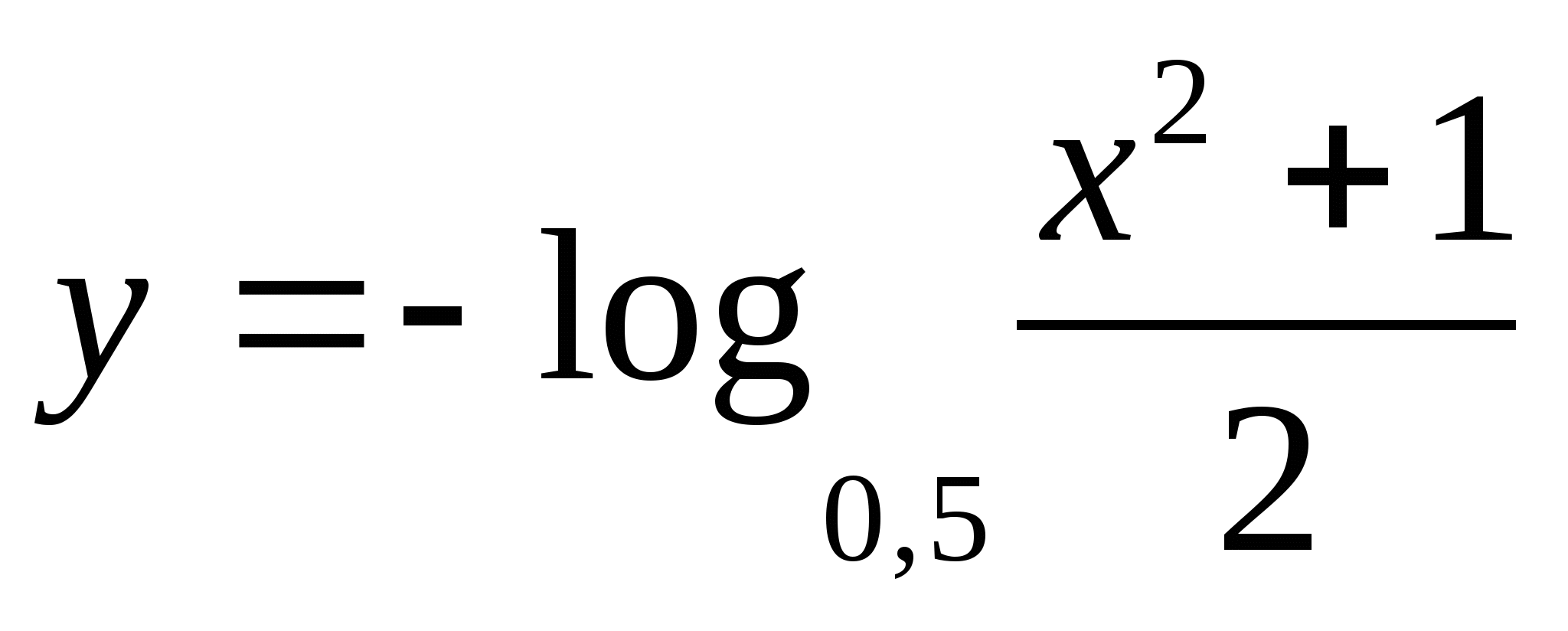 tussenin
tussenin 
1) -1/2 2) 5 3) 2 4) 4
8. Vind de som van alle natuurlijke getallen die niet zijn opgenomen in de waardensets van de functie 
1) 3 2) 6 3) 10 4) 8
Optie 6
1. Specificeer de grootste gehele waarde van de functie 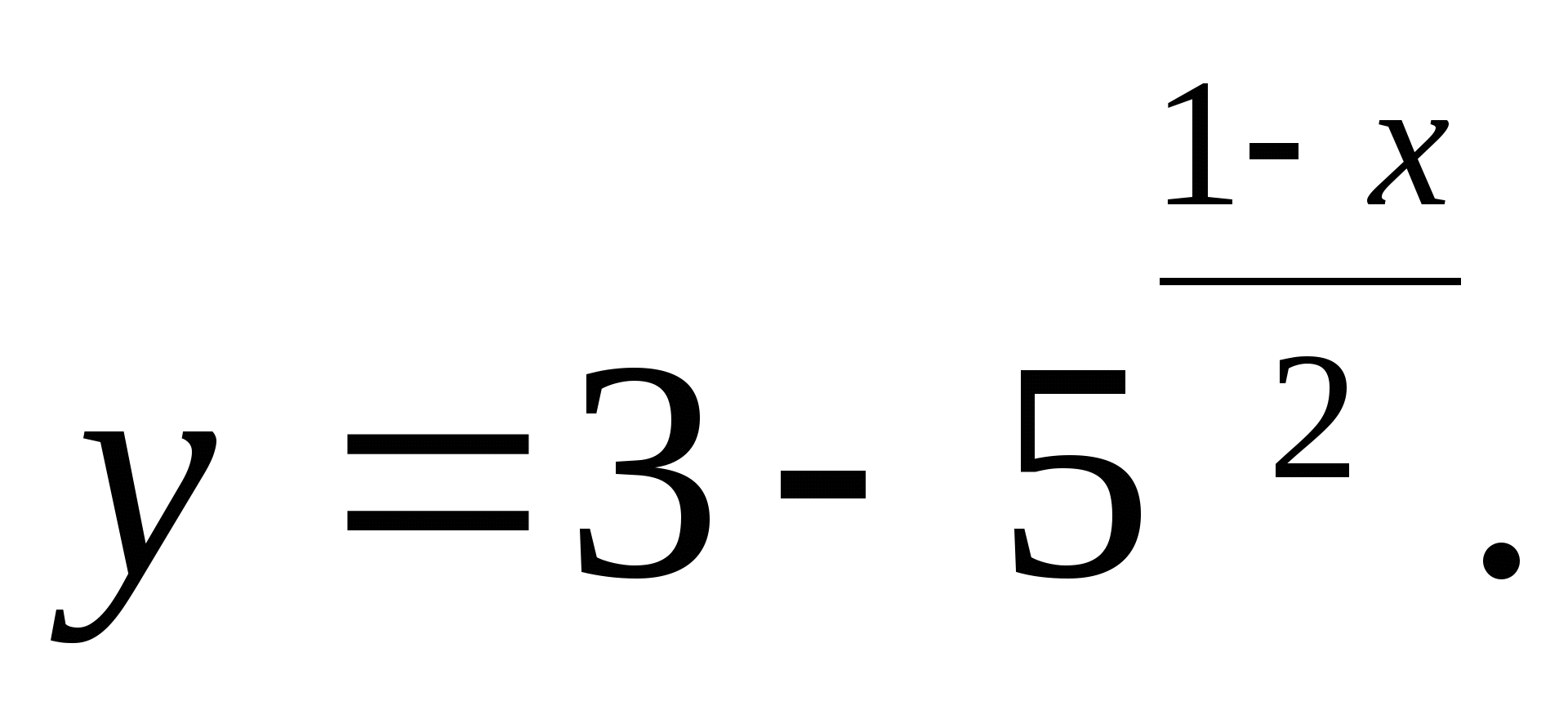
1) 2 2) 4 3) 3 4) 5
2. Welk van de volgende getallen valt niet binnen het bereik van de functie 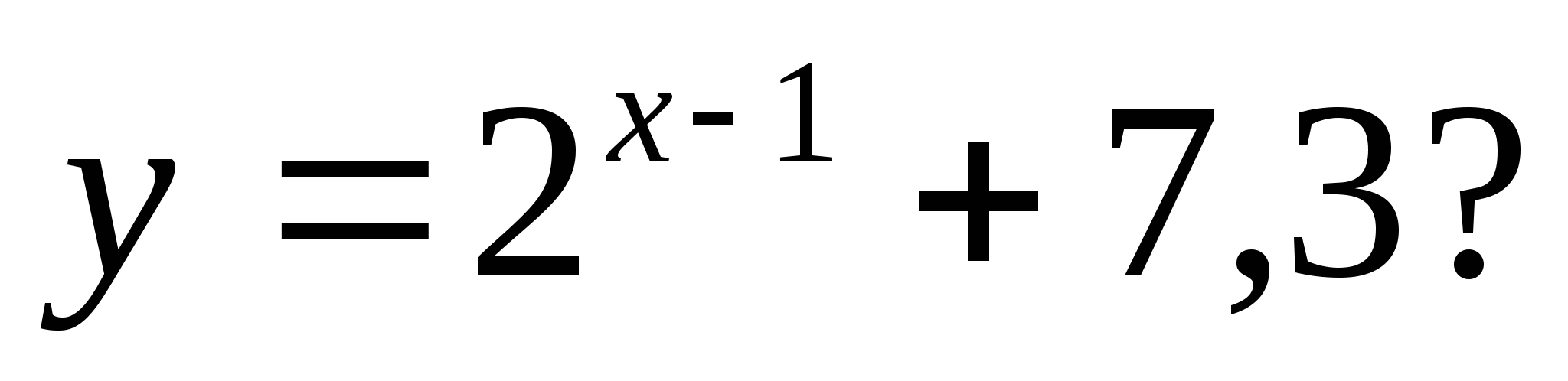
1) 35 2) 7, 28 3) 7, 85 4) 128
3. Specificeer een set functiewaarden 
1) [-1/3;0] 2) (-3;2/5) 3) (0;1/3) 4) (0;2/5)
4. Zoek alle punten op de OU die projecties zijn van de punten van de grafiek van de functie 
1) (0;∞) 2) 2) (-3;2) 3) [ log 2 3;2] 4) (log 2 3;2)
6. Zoek op welk segment de functie  neemt de kleinste waarde als -2 en de grootste waarde als 4.
neemt de kleinste waarde als -2 en de grootste waarde als 4.
1) [-17/9;79] 2) [-1,5;82] 3) (-11/9;79] 4) (-17/9;79)
7. Specificeer de grootste waarde van de functie  tussenin
tussenin
[-0,9; 0]. 2. Zoek de kleinste waarde van de functie op het segment.
4. Hoeveel gehele waarden heeft de functie nodig 
antwoorden
Deel 1
Set exponentiële en logaritmische functiewaarden
Deel 2
Veel taken leiden ertoe dat we zoeken naar een set functiewaarden op een bepaald segment of op het hele definitiedomein. Dergelijke taken omvatten verschillende evaluaties van uitdrukkingen, het oplossen van ongelijkheden.
In dit artikel zullen we het bereik van een functie definiëren, methoden overwegen om deze te vinden en de oplossing van voorbeelden van eenvoudig tot complexer in detail analyseren. Al het materiaal wordt voor de duidelijkheid voorzien van grafische illustraties. Dit artikel is dus een gedetailleerd antwoord op de vraag hoe je het bereik van een functie kunt vinden.
Definitie.
De reeks waarden van de functie y = f(x) op het interval X genaamd de verzameling van alle waarden van de functie die nodig is bij het herhalen van alles .
Definitie.
Het bereik van de functie y = f(x) wordt de verzameling van alle waarden van de functie genoemd die nodig is bij het herhalen van alle x uit het definitiedomein.
Het bereik van de functie wordt aangeduid als E(f) .
Het bereik van een functie en de reeks waarden van een functie zijn niet hetzelfde. Deze concepten worden als equivalent beschouwd als het interval X bij het vinden van de reeks waarden van de functie y = f(x) samenvalt met het domein van de functie.
Verwar ook het bereik van de functie niet met de variabele x voor de uitdrukking aan de rechterkant van de vergelijking y=f(x) . Het gebied van toegestane waarden van de variabele x voor de uitdrukking f(x) is het gebied van de definitie van de functie y=f(x) .
De figuur toont enkele voorbeelden.
Functiegrafieken worden weergegeven met dikke blauwe lijnen, dunne rode lijnen zijn asymptoten, rode stippen en lijnen op de Oy-as tonen het bereik van de corresponderende functie.

Zoals u kunt zien, wordt het bereik van de functie verkregen door de grafiek van de functie op de y-as te projecteren. Het kan een enkel getal zijn (eerste geval), een reeks getallen (tweede geval), een segment (derde geval), een interval (vierde geval), een open straal (vijfde geval), een unie (zesde geval), enz. .
Dus wat moet je doen om het bereik van de functie te vinden.
Laten we beginnen met het eenvoudigste geval: we zullen laten zien hoe we de reeks waarden van een continue functie y = f(x) op het interval kunnen bepalen.
Het is bekend dat een functie continu op een segment zijn maximale en minimale waarden erop bereikt. De reeks waarden van de originele functie op het segment zal dus het segment zijn ![]() . Daarom is onze taak beperkt tot het vinden van de grootste en kleinste waarden van de functie op het interval .
. Daarom is onze taak beperkt tot het vinden van de grootste en kleinste waarden van de functie op het interval .
Laten we bijvoorbeeld het bereik van de arcsinusfunctie zoeken.
Voorbeeld.
Specificeer het bereik van de functie y = arcsinx .
Oplossing.
Het definitiedomein van de arcsinus is het segment [-1; een] . Zoek de grootste en kleinste waarde van de functie op dit segment. 
De afgeleide is positief voor alle x uit het interval (-1; 1) , dat wil zeggen dat de boogsinusfunctie toeneemt over het hele definitiedomein. Daarom heeft het de kleinste waarde bij x = -1 en de grootste bij x = 1. 
We hebben het bereik van de arcsinusfunctie  .
.
Voorbeeld.
Zoek de set functiewaarden ![]() op het segment.
op het segment.
Oplossing.
Zoek de grootste en kleinste waarde van de functie op het gegeven segment.
Laten we de extreme punten die bij het segment horen definiëren: 
We berekenen de waarden van de originele functie aan de uiteinden van het segment en op punten ![]() :
:
Daarom is de reeks waarden van de functie op het segment het segment  .
.
Nu zullen we laten zien hoe we de reeks waarden van een continue functie y = f(x) in de intervallen (a; b) , kunnen vinden.
Eerst bepalen we de extremumpunten, de extrema van de functie, de intervallen van toename en afname van de functie op een bepaald interval. Vervolgens berekenen we aan de uiteinden van het interval en (of) de limieten op oneindig (dat wil zeggen, we bestuderen het gedrag van de functie op de grenzen van het interval of op oneindig). Deze informatie is voldoende om de set functiewaarden op dergelijke intervallen te vinden.
Voorbeeld.
Bepaal de set functiewaarden op het interval (-2; 2).
Oplossing.
Laten we de extreme punten van de functie zoeken die op het interval (-2; 2) vallen: 
Punt x = 0 is het maximale punt, aangezien de afgeleide van teken verandert van plus naar min als hij er doorheen gaat, en de grafiek van de functie van stijgend naar dalend gaat. 
![]() is het corresponderende maximum van de functie.
is het corresponderende maximum van de functie.
Laten we eens kijken naar het gedrag van de functie wanneer x neigt naar -2 aan de rechterkant en wanneer x neigt naar 2 aan de linkerkant, dat wil zeggen dat we eenzijdige limieten vinden: 
Wat we hebben: wanneer het argument verandert van -2 naar nul, nemen de functiewaarden toe van min oneindig tot min een kwart (het maximum van de functie bij x = 0 ), wanneer het argument verandert van nul naar 2, de functie waarden dalen tot min oneindig. De set functiewaarden op het interval (-2; 2) is dus .
Voorbeeld.
Specificeer de reeks waarden van de raaklijnfunctie y = tgx op het interval.
Oplossing.
De afgeleide van de raaklijnfunctie op het interval is positief ![]() , wat duidt op een toename van de functie. We bestuderen het gedrag van de functie op de grenzen van het interval:
, wat duidt op een toename van de functie. We bestuderen het gedrag van de functie op de grenzen van het interval: 
Dus wanneer het argument verandert van in, nemen de waarden van de functie toe van min oneindig tot plus oneindig, dat wil zeggen dat de reeks raaklijnwaarden in dit interval de verzameling is van alle reële getallen.
Voorbeeld.
Zoek het bereik van de natuurlijke logaritmefunctie y = lnx .
Oplossing.
De natuurlijke logaritmefunctie is gedefinieerd voor positieve waarden van het argument ![]() . Op dit interval is de afgeleide positief
. Op dit interval is de afgeleide positief ![]() , dit duidt op een toename van de functie erop. Laten we de eenzijdige limiet van de functie vinden als het argument neigt naar nul vanaf rechts, en de limiet als x neigt naar plus oneindig:
, dit duidt op een toename van de functie erop. Laten we de eenzijdige limiet van de functie vinden als het argument neigt naar nul vanaf rechts, en de limiet als x neigt naar plus oneindig: 
We zien dat als x verandert van nul naar plus oneindig, de waarden van de functie toenemen van min oneindig naar plus oneindig. Daarom is het bereik van de natuurlijke logaritmefunctie de volledige reeks reële getallen.
Voorbeeld.
Oplossing.
Deze functie is gedefinieerd voor alle reële x-waarden. Laten we de extreme punten bepalen, evenals de intervallen van toename en afname van de functie. 
Daarom neemt de functie af bij , neemt toe bij , x = 0 is het maximale punt, ![]() het bijbehorende maximum van de functie.
het bijbehorende maximum van de functie.
Laten we eens kijken naar het gedrag van de functie op oneindig: 
Dus op oneindig naderen de waarden van de functie asymptotisch nul.
We ontdekten dat wanneer het argument verandert van min oneindig naar nul (maximum punt), de functiewaarden toenemen van nul naar negen (tot het maximum van de functie), en wanneer x verandert van nul naar plus oneindig, de functiewaarden van negen naar nul te verlagen.
Kijk naar de schematische tekening.

Nu is duidelijk te zien dat het bereik van de functie .
Het vinden van de reeks waarden van de functie y = f(x) op intervallen vereist vergelijkbare studies. We zullen nu niet in detail op deze gevallen ingaan. We zullen ze in de onderstaande voorbeelden zien.
Laat het domein van de functie y = f(x) de vereniging zijn van meerdere intervallen. Bij het vinden van het bereik van een dergelijke functie, worden de reeksen waarden voor elk interval bepaald en wordt hun unie genomen.
Voorbeeld.
Zoek het bereik van de functie.
Oplossing.
De noemer van onze functie mag niet naar nul gaan, dat wil zeggen .
Laten we eerst de reeks waarden van de functie op de open straal zoeken.
Functie afgeleide  is negatief op dit interval, dat wil zeggen dat de functie erop afneemt.
is negatief op dit interval, dat wil zeggen dat de functie erop afneemt. 
We ontdekten dat, aangezien het argument de neiging heeft tot min oneindig, de waarden van de functie asymptotisch de eenheid benaderen. Wanneer x verandert van minus oneindig naar twee, nemen de waarden van de functie af van één naar minus oneindig, dat wil zeggen, op het beschouwde interval neemt de functie een reeks waarden aan. We nemen geen eenheid op, omdat de waarden van de functie deze niet bereiken, maar er alleen asymptotisch naar neigen op min oneindig.
We handelen op dezelfde manier voor een open balk.
De functie neemt ook af op dit interval. 
De set functiewaarden op dit interval is de set.
Het gewenste bereik van functiewaarden is dus de vereniging van de sets en .
Grafische illustratie.

Afzonderlijk moeten we stilstaan bij periodieke functies. Het bereik van periodieke functies valt samen met de reeks waarden op het interval dat overeenkomt met de periode van deze functie.
Voorbeeld.
Zoek het bereik van de sinusfunctie y = sinx .
Oplossing.
Deze functie is periodiek met een periode van twee pi. Laten we een segment nemen en de reeks waarden erop definiëren. 
Het segment bevat twee extreme punten en .
We berekenen de waarden van de functie op deze punten en op de grenzen van het segment, kies de kleinste en grootste waarden: 
Vervolgens, ![]() .
.
Voorbeeld.
Vind het bereik van een functie ![]() .
.
Oplossing.
We weten dat het bereik van de arccosinus het segment is van nul tot pi, dat wil zeggen, ![]() of in een ander bericht. Functie
of in een ander bericht. Functie ![]() kan worden verkregen uit arccosx door te verschuiven en uit te rekken langs de x-as. Dergelijke transformaties hebben geen invloed op het bereik, daarom
kan worden verkregen uit arccosx door te verschuiven en uit te rekken langs de x-as. Dergelijke transformaties hebben geen invloed op het bereik, daarom ![]() . Functie
. Functie ![]() komt van
komt van ![]() zich drie keer uitstrekken langs de Oy-as, dat wil zeggen,
zich drie keer uitstrekken langs de Oy-as, dat wil zeggen, ![]() . En de laatste fase van transformaties is een verschuiving met vier eenheden langs de y-as. Dit leidt ons naar een dubbele ongelijkheid
. En de laatste fase van transformaties is een verschuiving met vier eenheden langs de y-as. Dit leidt ons naar een dubbele ongelijkheid 
Het gewenste waardenbereik is dus ![]() .
.
Laten we een oplossing geven voor een ander voorbeeld, maar zonder uitleg (ze zijn niet vereist, omdat ze volledig op elkaar lijken).
Voorbeeld.
Functiebereik definiëren ![]() .
.
Oplossing.
We schrijven de originele functie in de vorm ![]() . Het bereik van de exponentiële functie is het interval . Dat is, . Dan
. Het bereik van de exponentiële functie is het interval . Dat is, . Dan 
Vervolgens, ![]() .
.
Om het plaatje compleet te maken, moeten we het hebben over het vinden van het bereik van een functie die niet continu is op het domein van definitie. In dit geval wordt het definitiedomein door breekpunten verdeeld in intervallen en vinden we de reeksen waarden op elk van hen. Door de verkregen reeksen waarden te combineren, verkrijgen we het waardenbereik van de oorspronkelijke functie. We raden aan om 3 links te onthouden, de waarden van de functie neigen naar min één, en wanneer x neigt naar 3 aan de rechterkant, neigen de waarden van de functie naar plus oneindig.
Het definitiedomein van de functie is dus verdeeld in drie intervallen.
Op het interval hebben we de functie ![]() . Vanaf dat moment
. Vanaf dat moment 
De reeks waarden van de oorspronkelijke functie op het interval is dus [-6;2] .
Op het halve interval hebben we een constante functie y = -1 . Dat wil zeggen, de reeks waarden van de oorspronkelijke functie op het interval bestaat uit een enkel element .
De functie is gedefinieerd voor alle geldige waarden van het argument. Ontdek de intervallen van toename en afname van de functie.
De afgeleide verdwijnt bij x=-1 en x=3 . We markeren deze punten op de reële as en bepalen de tekens van de afgeleide op de verkregen intervallen. 
De functie neemt af met ![]() , neemt toe met [-1; 3] , x=-1 minimum punt, x=3 maximum punt.
, neemt toe met [-1; 3] , x=-1 minimum punt, x=3 maximum punt.
We berekenen de bijbehorende minimum- en maximumfuncties: 
Laten we het gedrag van de functie op oneindig controleren: 
De tweede limiet werd berekend vanaf .
Laten we een schematische tekening maken.
Als het argument verandert van min oneindig naar -1, dan nemen de functiewaarden af van plus oneindig naar -2e, als het argument verandert van -1 naar 3, nemen de functiewaarden toe van -2e naar , als het argument verandert van 3 tot plus oneindig, de functiewaarden dalen van naar nul, maar ze bereiken geen nul.

Pagina 1
Les 3
"functiebereik"
Doelstellingen: - Pas het concept van het waardenbereik toe op de oplossing van een specifiek probleem;
typische problemen oplossen.
Sinds enkele jaren doen zich regelmatig problemen voor bij examens waarin het nodig is om uit een bepaalde familie van functies die te selecteren waarvan de reeksen waarden voldoen aan de verklaarde voorwaarden.
Laten we eens kijken naar dergelijke taken.
Kennis update.
Wat bedoelen we met de verzameling functiewaarden?
Wat is de waardenset van een functie?
Uit welke gegevens kunnen we de set functiewaarden vinden? (Volgens de analytische notatie van de functie of zijn grafiek)
(zie USE opdrachten, deel A)
Welke functiewaarden kennen we? (De belangrijkste functies worden vermeld met hun schrift op het bord, voor elk van de functies wordt de reeks waarden opgeschreven). Daardoor staan op het bord en in de schriften van de leerlingen
|
Functie |
Veel waarden |
|
ja = x 2 ja = x 3 y=| x| y=
|
E( ja) = E( ja) = [- 1, 1] E( ja) = (– ∞, + ∞) E( ja) = (– ∞, + ∞) E( ja) = (– ∞, + ∞) E( ja) = (0, + ∞) |
Kunnen we, met behulp van deze kennis, onmiddellijk de waardensets vinden van de functies die op het bord zijn geschreven? (zie tabel 2).
Wat kan helpen bij het beantwoorden van deze vraag? (Grafieken van deze functies).
Hoe de eerste functie plotten? (Verlaag de parabool 4 eenheden naar beneden).
|
Functie |
Veel waarden |
|
ja = x 2 – 4 |
E( ja) = [-4, + ∞) |
|
ja = + 5 |
E( ja) = |
|
ja = – 5cos x |
E( ja) = [- 5, 5] |
|
y= tg( x + / 6) – 1 |
E( ja) = (– ∞, + ∞) |
|
y= zonde( x + / 3) – 2 |
E( ja) = [- 3, - 1] |
|
y=| x – 1 | + 3 |
E( ja) = |
|
y=| ctg x| |
E( ja) = |
|
ja =  = | cos(x + /4) | = | cos(x + /4) | |
E( ja) = |
|
y=(x- 5) 2 + 3 |
E( ja) = . Zoek de set functiewaarden:   . 
Introductie van een algoritme voor het oplossen van problemen voor het vinden van de reeks waarden van trigonometrische functies. Laten we eens kijken hoe we onze ervaring kunnen toepassen om verschillende taken op te lossen die deel uitmaken van de opties voor een enkel examen. 1. De waarden van functies vinden voor een gegeven waarde van het argument. Voorbeeld. Vind de waarde van de functie y = 2 omdat(π/2+ π/4 ) – 1, als x = -/2. Oplossing. ja(-π/2) = 2 omdat(- π/2 – π/4 )- 1= 2 omdat(π/2 + π/4 )- 1 = - 2 zondeπ/4 – 1 = - 2  – 1 = – 1 =
= – 2. Het bereik van trigonometrische functies vinden
1≤ zondeX≤ 1 2 ≤ 2 zondeX≤ 2 9 ≤ 11+2zondeX≤ 13 3 ≤ Laten we de gehele waarden van de functie op het interval uitschrijven. Dit aantal is 3. Antwoord: 3.
Bij= zonde 2 X- 2 3 zondex + 3 2 - 3 2 + 8, Bij= (zondeX- 3) 2 -1. e ( zondeX) = [-1;1]; e ( zondeX -3) = [-4;-2]; e ( zondeX -3) 2 = ; e ( Bij) = . Antwoorden: .
Kunnen we een reeks waarden voor deze functie vinden? (Niet.) Wat moet er gedaan worden? (Gereduceerd tot één functie.) Hoe je dat doet? (Gebruik formule cos 2 x= 1-zonde 2 x.) Dus, Bij= 1-zonde 2 x+2sin x –2, ja= -sin 2 x+2sin x –1, Bij= -(sin x –1) 2 . Welnu, nu kunnen we een reeks waarden vinden en de kleinste ervan kiezen. 1 zonde x ≤ 1, 2 zonde x – 1 ≤ 0, 0 ≤ (zonde) x – 1) 2 ≤ 4, 4 ≤ -(sin x -1) 2 ≤ 0. Dus de kleinste waarde van de functie Bij arbeidskracht= -4. Antwoord: -4.
Oplossing. Bij= 1-cos 2 x+ cos x + 1,5, Bij= -cos 2 x+ 2∙0,5∙cos x - 0,25 + 2,75, Bij= -(cos x- 0,5) 2 + 2,75. E(cos x) = [-1;1], E(cos x – 0,5) = [-1,5;0,5], E(cos x – 0,5) 2 = , E(-(cos x-0,5) 2) = [-2,25;0], E( Bij) = . De grootste waarde van de functie Bij naib= 2,75; kleinste waarde Bij arbeidskracht= 0,5. Laten we het product van de grootste en kleinste waarde van de functie zoeken: Bij naib ∙Bij arbeidskracht = 0,5∙2,75 = 1,375. Antwoord: 1.375. Oplossing. Laten we de functie herschrijven in de vorm Bij =, Bij = Laten we nu de reeks waarden van de functie vinden. E(sin x) = [-1, 1], E(6sin x) = [-6, 6], E(6sin x + 1) = [-5, 7], E((6sin x + 1) 2) = , E(– (6sin x + 1) 2) = [-49, 0], E(– (6sin x + 1) 2 + 64) = , E( ja) = [ Laten we de som van gehele waarden van de functie vinden: 4 + 5 + 6 + 7 + 8 = 30. Antwoord: 30.  Oplossing. 1) 2) daarom, 2 X behoren tot het tweede kwartaal. 3) In het tweede kwartaal neemt de sinusfunctie af en is continu. Dus deze functie 4) Bereken deze waarden:
Antwoorden :
 Oplossing. 1) Aangezien een sinus waarden aanneemt van -1 tot 1, dan is de reeks verschilwaarden 2) De arccosinus is een monotoon afnemende en continue functie. Daarom is de reeks waarden van de uitdrukking een segment 3) Bij vermenigvuldiging van dit segment met Antwoorden:  Oplossing. Aangezien de boogtangens een toenemende functie is, dan: 2) Bij het verhogen X van 3) Bij het verhogen van 4) Met behulp van de formule die de sinus uitdrukt in termen van de tangens van een halve hoek, vinden we dat
Daarom is de gewenste reeks waarden de vereniging van segmenten Antwoorden: Bij= een zonde x + b cos x of Bij= een zonde(Rx) + bcos(Rx).
Oplossing. Laten we de waarde vinden Laten we de uitdrukking transformeren 15 zonde 2x + 20 cos 2x = 25 ( 25 zonde (2x + De set functiewaarden y \u003d sin (2x + Dan de reeks waarden van de originele functie -25 Antwoorden:
[-25; 25].
Functie Bij= ctg X neemt af op het segment [π/4; π/2], daarom zal de functie de kleinste waarde aannemen bij x =π/2, dat wil zeggen Bij(π/2) = сtg π/2 = 0; en de grootste waarde is at x=π/4, dat wil zeggen Bij(π/4) = сtg π/4 = 1. Antwoord: 1, 0.  . Oplossing. Scheid in gelijkheid Hieruit volgt dat de grafiek van de functie f(x) ofwel een hyperbool (а≠ 0) of een rechte lijn zonder punt is. Bovendien, als een; 2a) en (2a; Als a \u003d 0, dan f (x) \u003d -2 over het hele definitiedomein x ≠ 0. Daarom is het duidelijk dat de gewenste waarden van de parameter niet gelijk zijn aan nul. Omdat we alleen geïnteresseerd zijn in de waarden van de functie op het segment [-1; 1], dan wordt de classificatie van situaties bepaald door het feit dat de asymptoot x = 2a van de hyperbool (a≠0) zich ten opzichte van dit segment bevindt. Geval 1. Alle punten van het interval [-1; 1] zijn rechts van de verticale asymptoot x = 2a, dat wil zeggen, wanneer 2a Geval 2. De verticale asymptoot snijdt het interval [-1; 1], en de functie neemt af (zoals in geval 1), dat wil zeggen, wanneer Geval 3. De verticale asymptoot snijdt het interval [-1; 1] en de functie neemt toe, d.w.z. -1 Geval 4. Alle punten van het interval [-1; 1] bevinden zich links van de verticale asymptoot, dat wil zeggen 1 a > . en ten tweede Receptie 5. Vereenvoudiging van de formule die een fractionele rationale functie definieert Ontvangst 6. De reeks waarden van kwadratische functies vinden (door het hoekpunt van de parabool te vinden en de aard van het gedrag van zijn takken vast te stellen). Receptie 7. Introductie van een hulphoek voor het vinden van de reeks waarden van sommige trigonometrische functies. Functie y=f(x) is zo'n afhankelijkheid van de variabele y van de variabele x wanneer elke geldige waarde van de variabele x overeenkomt met een enkele waarde van de variabele y . Functiebereik: D(f) is de verzameling van alle mogelijke waarden van de variabele x . Functiebereik: E(f) is de verzameling van alle geldige waarden van de variabele y . Functie Grafiek y=f(x) is de verzameling vlakke punten waarvan de coördinaten voldoen aan de gegeven functionele afhankelijkheid, dat wil zeggen punten van de vorm M (x; f(x)) . De grafiek van een functie is een lijn op een vlak. Als b=0 , dan heeft de functie de vorm y=kx en wordt genoemd directe evenredigheid. D(f) : x \in R;\enspace E(f) : y \in R De grafiek van een lineaire functie is een rechte lijn. De helling k van de rechte y=kx+b wordt berekend met de volgende formule: k= tg \alpha , waarbij \alpha de hellingshoek is van de rechte lijn met de positieve richting van de Ox-as. 1) De functie neemt monotoon toe voor k > 0 . Bijvoorbeeld: y=x+1 2) De functie neemt monotoon af als k< 0 . Bijvoorbeeld: y=-x+1
3) Als k=0 , dan krijgen we b willekeurige waarden, dan krijgen we een familie van rechte lijnen evenwijdig aan de as Ox . Bijvoorbeeld: y=-1
Omgekeerde evenredigheidOmgekeerde evenredigheid heet een functie van de vorm y=\frac (k)(x), waarbij k een reëel getal is dat niet nul is D(f) : x \in \links \( R/x \neq 0 \rechts \); \: E(f) : y \in \links \(R/y \neq 0 \right \). Functie Grafiek y=\frac (k)(x) is een hyperbool. 1) Als k > 0, dan zal de grafiek van de functie zich in het eerste en derde kwart van het coördinatenvlak bevinden. Bijvoorbeeld: y=\frac(1)(x)
2) Als k< 0 , то график функции будет располагаться во второй и четвертой координатной плоскости. Bijvoorbeeld: y=-\frac(1)(x)
Power functiePower functie is een functie van de vorm y=x^n , waarbij n een reëel getal is dat niet nul is 1) Als n=2 , dan y=x^2 . D(f) : x \in R; \: E(f) : y \in; hoofdperiode van de functie T=2 \pi Categorieën
|


 – 1.
– 1.
 , d.w.z. E (y) = .
, d.w.z. E (y) = . ,
,
 , 8].
, 8]. dat is X behoort tot het eerste kwartaal.
dat is X behoort tot het eerste kwartaal.
 voordat
voordat 


 .
.
 . Wanneer vermenigvuldigd met
. Wanneer vermenigvuldigd met  dit segment gaat naar het segment
dit segment gaat naar het segment  .
. .
. we krijgen
we krijgen  .
. .
.
 .
. voordat
voordat  argument 2 X stijgt van
argument 2 X stijgt van  voordat
voordat  . Aangezien de sinus op zo'n interval toeneemt, is de functie
. Aangezien de sinus op zo'n interval toeneemt, is de functie  tot 1.
tot 1. argument 2 X stijgt van
argument 2 X stijgt van  . Omdat de sinus op zo'n interval afneemt, is de functie
. Omdat de sinus op zo'n interval afneemt, is de functie  tot 1.
tot 1.
 .
. en
en  , dat wil zeggen, het segment
, dat wil zeggen, het segment  =
=  = 25.
= 25. ) = 25 () =
) = 25 () = ), waar mede
), waar mede  zonde (2x +
zonde (2x +  ) en, als a > 0, monotoon toeneemt op deze stralen.
) en, als a > 0, monotoon toeneemt op deze stralen.
 .
.






