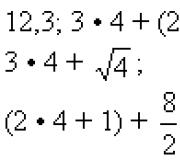Afbeelding van natuurlijke getallen door stippen op een getallenlijn. Modulus van getal (absolute waarde van getal), definities, voorbeelden, eigenschappen

We weten al dat de verzameling reële getallen $R$ wordt gevormd door rationale en irrationele getallen.

Rationele getallen kunnen altijd worden weergegeven als decimalen (eindig of oneindig periodiek).

Irrationele getallen worden geschreven als oneindige maar niet-recurrente decimalen.

De verzameling reële getallen $R$ bevat ook de elementen $-\infty $ en $+\infty $, waarvoor de ongelijkheden $-\infty

Overweeg manieren om reële getallen weer te geven.

Gemeenschappelijke breuken

Gewone breuken worden geschreven met twee natuurlijke getallen en een horizontale breukstreep. De fractionele balk vervangt eigenlijk het deelteken. Het getal onder de lijn is de noemer (deler), het getal boven de lijn is de teller (deelbaar).

Definitie

Een breuk wordt juist genoemd als de teller kleiner is dan de noemer. Omgekeerd wordt een breuk oneigenlijk genoemd als de teller groter is dan of gelijk is aan de noemer.

Voor gewone breuken zijn er eenvoudige, praktisch voor de hand liggende vergelijkingsregels ($m$,$n$,$p$ zijn natuurlijke getallen):

van twee breuken met dezelfde noemers, is die met de grotere teller groter, d.w.z. $\frac(m)(p) >\frac(n)(p) $ voor $m>n$;
van twee breuken met dezelfde tellers, is die met de kleinere noemer groter, d.w.z. $\frac(p)(m) >\frac(p)(n) $ voor $ m
een juiste breuk is altijd kleiner dan één; onjuiste breuk is altijd groter dan één; een breuk waarvan de teller gelijk is aan de noemer is gelijk aan één;
Elke oneigenlijke breuk is groter dan elke juiste breuk.

Decimale getallen

De notatie van een decimaal getal (decimale breuk) heeft de vorm: geheel getal, decimale punt, breukdeel. De decimale notatie van een gewone breuk kan worden verkregen door de "hoek" van de teller te delen door de noemer. Dit kan resulteren in een eindige decimale breuk of een oneindige periodieke decimale breuk.

Definitie

De fractionele cijfers worden decimalen genoemd. In dit geval wordt het eerste cijfer achter de komma het tiende cijfer genoemd, het tweede - het honderdste cijfer, het derde - het duizendste cijfer, enz.

voorbeeld 1

We bepalen de waarde van het decimale getal 3,74. We krijgen: $3,74=3+\frac(7)(10) +\frac(4)(100) $.

Het decimale getal kan worden afgerond. In dit geval moet u het cijfer opgeven waarop wordt afgerond.

De afrondingsregel is als volgt:

alle cijfers rechts van dit cijfer worden vervangen door nullen (als deze cijfers voor de komma staan) of worden weggegooid (als deze cijfers achter de komma staan);
als het eerste cijfer dat volgt op het gegeven cijfer kleiner is dan 5, wordt het cijfer van dit cijfer niet gewijzigd;
als het eerste cijfer dat volgt op het gegeven cijfer 5 of meer is, wordt het cijfer van dit cijfer met één verhoogd.

Voorbeeld 2

Laten we het getal 17302 afronden op het dichtstbijzijnde duizendtal: 17.000.
Laten we het getal 17378 afronden op het dichtstbijzijnde honderdtal: 17400.
Laten we het getal 17378,45 afronden op tientallen: 17380.
Laten we het getal 378.91434 afronden op het dichtstbijzijnde honderdtal: 378.91.
Laten we het getal 378.91534 afronden op het dichtstbijzijnde honderdtal: 378.92.

Een decimaal getal converteren naar een gewone breuk.

Zaak 1

Een decimaal getal is een einddecimaal.

De conversiemethode wordt getoond in het volgende voorbeeld.

Voorbeeld 2

We hebben: $3.74=3+\frac(7)(10) +\frac(4)(100) $.

Reduceer tot een gemeenschappelijke noemer en krijg:

De breuk kan worden verkleind: $3.74=\frac(374)(100) =\frac(187)(50) $.

Geval 2

Een decimaal getal is een oneindig terugkerend decimaal getal.

De transformatiemethode is gebaseerd op het feit dat het periodieke deel van een periodieke decimale breuk kan worden beschouwd als de som van leden van een oneindig afnemende geometrische progressie.

Voorbeeld 4

$0,\left(74\right)=\frac(74)(100) +\frac(74)(10000) +\frac(74)(1000000) +\ldots $. Het eerste lid van de progressie is $a=0.74$, de noemer van de progressie is $q=0.01$.

Voorbeeld 5

$0.5\left(8\right)=\frac(5)(10) +\frac(8)(100) +\frac(8)(1000) +\frac(8)(10000) +\ldots $ . Het eerste lid van de progressie is $a=0.08$, de noemer van de progressie is $q=0.1$.

De som van de termen van een oneindig afnemende meetkundige progressie wordt berekend met de formule $s=\frac(a)(1-q) $, waarbij $a$ de eerste term is en $q$ de noemer is van de progressie $ \links (0

Voorbeeld 6

Laten we de oneindige periodieke decimale breuk $0,\left(72\right)$ omzetten in een gewone.

Het eerste lid van de progressie is $a=0.72$, de noemer van de progressie is $q=0.01$. We krijgen: $s=\frac(a)(1-q) =\frac(0.72)(1-0.01) =\frac(0.72)(0.99) =\frac(72)( 99) =\frac(8 )(11) $. Dus $0,\left(72\right)=\frac(8)(11) $.

Voorbeeld 7

Laten we de oneindige periodieke decimale breuk $0.5\left(3\right)$ omzetten in een gewone.

Het eerste lid van de progressie is $a=0.03$, de noemer van de progressie is $q=0.1$. We krijgen: $s=\frac(a)(1-q) =\frac(0.03)(1-0.1) =\frac(0.03)(0.9) =\frac(3)( 90) =\frac(1 )(30)$.

Dus $0.5\left(3\right)=\frac(5)(10) +\frac(1)(30) =\frac(5\cdot 3)(10\cdot 3) +\frac( 1)(30 ) =\frac(15)(30) +\frac(1)(30) =\frac(16)(30) =\frac(8)(15) $.

Reële getallen kunnen worden weergegeven door punten op de getallenlijn.

In dit geval noemen we de numerieke as een oneindige lijn waarop de oorsprong (punt $O$), positieve richting (aangegeven door een pijl) en schaal (om waarden weer te geven) zijn geselecteerd.

Tussen alle reële getallen en alle punten van de numerieke as is er een één-op-één overeenkomst: elk punt komt overeen met één enkel cijfer en omgekeerd komt elk cijfer overeen met één enkel punt. Daarom is de verzameling reële getallen continu en oneindig op dezelfde manier als de getallenlijn continu en oneindig is.

Sommige deelverzamelingen van de verzameling reële getallen worden numerieke intervallen genoemd. De elementen van een numeriek interval zijn getallen $x\in R$ die aan een bepaalde ongelijkheid voldoen. Laat $a\in R$, $b\in R$ en $a\le b$. In dit geval kunnen de soorten hiaten als volgt zijn:

Interval $\links(a,\;b\rechts)$. Tegelijkertijd $ a
Segment $\left$. Bovendien, $a\le x\le b$.
Halve segmenten of halve intervallen $\left$. Tegelijkertijd $ a \le x
Oneindige overspanningen, bijv. $a

Van groot belang is ook een soort interval, de buurt van een punt genoemd. De buurt van een gegeven punt $x_(0) \in R$ is een willekeurig interval $\left(a,\;b\right)$ dat dit punt in zichzelf bevat, d.w.z. $a 0$ - 10e straal.

De absolute waarde van het getal

De absolute waarde (of modulus) van een reëel getal $x$ is een niet-negatief reëel getal $\left|x\right|$, gedefinieerd door de formule: $\left|x\right|=\left\(\ begin(array)(c) (\; \; x\; \; (\rm aan)\; \; x\ge 0) \\ (-x\; \; (\rm aan)\; \; x

Geometrisch betekent $\left|x\right|$ de afstand tussen de punten $x$ en 0 op de reële as.

Eigenschappen van absolute waarden:

uit de definitie volgt dat $\left|x\right|\ge 0$, $\left|x\right|=\left|-x\right|$;
voor de modulus van de som en voor de modulus van het verschil van twee getallen, de ongelijkheden $\left|x+y\right|\le \left|x\right|+\left|y\right|$, $\ left|x-y\right|\le \left|x\right|+\left|y\right|$ en ook $\left|x+y\right|\ge \left|x\right|-\left|y \right|$,$\ left|x-y\right|\ge \left|x\right|-\left|y\right|$;
de modulus van het product en de modulus van het quotiënt van twee getallen voldoen aan de gelijkheden $\left|x\cdot y\right|=\left|x\right|\cdot \left|y\right|$ en $\left |\frac(x)( y) \right|=\frac(\left|x\right|)(\left|y\right|) $.

Op basis van de definitie van de absolute waarde voor een willekeurig getal $a>0$ kan men ook de gelijkwaardigheid van de volgende ongelijkhedenparen vaststellen:

als $ \links|x\rechts|
als $\left|x\right|\le a$ dan $-a\le x\le a$;
als $\left|x\right|>a$ dan ofwel $xa$;
als $\left|x\right|\ge a$, dan $x\le -a$ of $x\ge a$.

Voorbeeld 8

Los de ongelijkheid $\left|2\cdot x+1\right| . op

Deze ongelijkheid is gelijk aan de ongelijkheid $-7

Vanaf hier krijgen we: $ -8

Een getallenlijn, een getallenas, is een lijn waarop reële getallen zijn afgebeeld. Op de rechte lijn wordt de oorsprong gekozen - het punt O (punt O staat voor 0) en het punt L, dat de eenheid vertegenwoordigt. Het punt L staat meestal rechts van het punt O. Het segment OL wordt het eenheidssegment genoemd.

De punten rechts van punt O vertegenwoordigen positieve getallen. Stippen links van de stip. Oh, geef negatieve getallen weer. Als het punt X een positief getal x voorstelt, dan is de afstand OX = x. Als het punt X een negatief getal x voorstelt, dan is de afstand OX = - x.

Het getal dat de positie van een punt op een rechte lijn aangeeft, wordt de coördinaat van dit punt genoemd.

Punt V in de afbeelding heeft een coördinaat van 2 en punt H heeft een coördinaat van -2.6.

De modulus van een reëel getal is de afstand van de oorsprong tot het punt dat overeenkomt met dit getal. Geef de modulus van het getal x aan, dus: | x |. Het is duidelijk dat | 0 | = 0.

Als het getal x groter is dan 0, dan is | x | = x, en als x kleiner is dan 0, dan | x | = - x. Op deze eigenschappen van de module is de oplossing van vele vergelijkingen en ongelijkheden met de module gebaseerd.

Voorbeeld: Los vergelijking | . op x - 3 | = 1.

Oplossing: Overweeg twee gevallen - het eerste geval, wanneer x -3 > 0, en het tweede geval, wanneer x - 3 0.

1. x - 3 > 0, x > 3.

In dit geval | x - 3 | = x - 3.

De vergelijking heeft de vorm x - 3 \u003d 1, x \u003d 4. 4\u003e 3 - voldoet aan de eerste voorwaarde.

2. x -3 0, x 3.

In dit geval | x - 3 | = - x + 3

De vergelijking heeft de vorm x + 3 \u003d 1, x \u003d - 2. -2 3 - voldoet aan de tweede voorwaarde.

Antwoord: x = 4, x = -2.

Numerieke uitdrukkingen.

Een numerieke uitdrukking is een verzameling van een of meer getallen en functies die zijn verbonden door rekenkundige operatoren en haakjes.
Voorbeelden van numerieke uitdrukkingen:

De waarde van een numerieke uitdrukking is een getal.
Bewerkingen in numerieke expressie worden in de volgende volgorde uitgevoerd:

1. Acties tussen haakjes.

2. Berekening van functies.

3. Machtsverheffing

4. Vermenigvuldigen en delen.

5. Optellen en aftrekken.

6. Bewerkingen van hetzelfde type worden van links naar rechts uitgevoerd.

Dus de waarde van de eerste uitdrukking is het getal zelf 12.3
Om de waarde van de tweede uitdrukking te berekenen, voeren we de acties in de volgende volgorde uit:

1. Voer de acties tussen haakjes in de volgende volgorde uit - eerst verhogen we 2 tot de derde macht en trekken dan 11 af van het resulterende getal:

3 4 + (23 - 11) = 3 4 + (8 - 11) = 3 4 + (-3)

2. Vermenigvuldig 3 met 4:

3 4 + (-3) = 12 + (-3)

3. Voer de bewerkingen achtereenvolgens van links naar rechts uit:

12 + (-3) = 9.
Een uitdrukking met variabelen is een verzameling van een of meer getallen, variabelen en functies verbonden door rekenkundige operatoren en haakjes. De waarden van expressies met variabelen zijn afhankelijk van de waarden van de variabelen die erin zijn opgenomen. De volgorde van bewerkingen is hier hetzelfde als voor numerieke uitdrukkingen. Het is soms handig om uitdrukkingen met variabelen te vereenvoudigen door verschillende acties uit te voeren - haakjes, uitbreiding van haakjes, groeperen, verkleinen van breuken, verkleinen van soortgelijke, enz. Om uitdrukkingen te vereenvoudigen, worden ook vaak verschillende formules gebruikt, bijvoorbeeld verkorte vermenigvuldigingsformules, eigenschappen van verschillende functies, enz.

Algebraïsche uitdrukkingen.

Een algebraïsche uitdrukking is een of meer algebraïsche grootheden (cijfers en letters) die met elkaar zijn verbonden door tekens van algebraïsche bewerkingen: optellen, aftrekken, vermenigvuldigen en delen, evenals het extraheren van de wortel en het verheffen tot een geheel getal (bovendien moeten de wortel en exponent noodzakelijkerwijs gehele getallen zijn) en tekens van de volgorde van deze acties (meestal verschillende soorten haakjes). Het aantal waarden in de algebraïsche uitdrukking moet eindig zijn.

Een voorbeeld van een algebraïsche uitdrukking:

"Algebraïsche uitdrukking" is een syntactisch concept, dat wil zeggen, iets is een algebraïsche uitdrukking als en alleen als het aan bepaalde grammaticale regels voldoet (zie Formele grammatica). Als de letters in een algebraïsche uitdrukking als variabelen worden beschouwd, krijgt de algebraïsche uitdrukking de betekenis van een algebraïsche functie.

nr. 1. Eigenschappen van rationale getallen.

 ordelijkheid . Voor alle rationale getallen en er is een regel waarmee u er één en slechts één van de drie op unieke wijze tussen kunt identificeren relaties: "", "" of "". Deze regel heet bestelregel en is als volgt geformuleerd: twee positieve getallen zijn verbonden door dezelfde relatie als twee gehele getallen; twee niet-positieve getallen en zijn gerelateerd door dezelfde relatie als twee niet-negatieve getallen en; als plotseling niet negatief, maar negatief, dan.

optelling van breuken

 Toevoeging: . sommatie regel, waardoor ze in overeenstemming zijn met een of ander rationaal getal . In dit geval wordt het nummer zelf genoemd som getallen u wordt aangegeven, en het proces om zo'n getal te vinden heet sommatie. De sommatieregel heeft de volgende vorm: .

 vermenigvuldiging operatie . Voor alle rationale getallen en er is een zogenaamde vermenigvuldigingsregel, waardoor ze in overeenstemming zijn met een of ander rationaal getal . In dit geval wordt het nummer zelf genoemd het werk getallen ii wordt aangeduid, en het proces om zo'n getal te vinden wordt ook wel vermenigvuldiging. De vermenigvuldigingsregel is als volgt: .

 transitiviteit relaties bestellen. Voor elk triplet van rationale getallen, en als minder en minder, dan minder, en als gelijk en gelijk, dan gelijk.

 commutativiteit toevoeging. Door een verandering in de plaatsen van rationele termen, verandert de som niet.

 Associativiteit toevoeging. De volgorde waarin drie rationale getallen worden opgeteld, heeft geen invloed op het resultaat.

 Beschikbaarheidnul . Er is een rationaal getal 0 dat elk ander rationaal getal behoudt wanneer het wordt opgeteld.

 De aanwezigheid van tegenovergestelde nummers. Elk rationaal getal heeft een tegengesteld rationaal getal, dat bij optelling 0 geeft.

 Commutativiteit van vermenigvuldiging. Door de plaatsen van rationele factoren te veranderen, verandert het product niet.

 Associativiteit van vermenigvuldiging. De volgorde waarin drie rationale getallen worden vermenigvuldigd, heeft geen invloed op het resultaat.

 Beschikbaarheideenheden . Er is een rationaal getal 1 dat elk ander rationaal getal behoudt wanneer het wordt vermenigvuldigd.

 Beschikbaarheidwederkerige nummers . Elk rationaal getal dat niet nul is, heeft een invers rationaal getal, waarbij vermenigvuldiging 1 geeft.

 distributiviteit vermenigvuldigen met betrekking tot optellen. De vermenigvuldigingsbewerking is consistent met de optelbewerking via de distributiewet:

 Verbinding van de orderrelatie met de bewerking van optellen. Hetzelfde rationele getal kan aan de linker- en rechterkant van een rationale ongelijkheid worden toegevoegd.

 Verbinding van de orderelatie met de bewerking van vermenigvuldiging. De linker- en rechterkant van een rationale ongelijkheid kunnen worden vermenigvuldigd met hetzelfde positieve rationale getal.

 Axioma van Archimedes . Wat het rationale getal ook is, je kunt zoveel eenheden nemen dat hun som groter zal zijn.

nr. 2. Modulus van een reëel getal.

Definitie . De modulus van een niet-negatief reëel getal x is het getal zelf: | x | = x; de modulus van een negatief reëel getal x is het tegenovergestelde getal: I x | = - x.

In het kort is het zo geschreven:

2. De geometrische betekenis van de modulus van een reëel getal

Laten we terugkeren naar de verzameling R van reële getallen en zijn geometrische modellen- getallenlijn. We markeren twee punten a en b op de lijn (twee reële getallen a en b), geven aan met (a, b) de afstand tussen de punten a en b (- de letter van het Griekse alfabet "ro"). Deze afstand is gelijk aan b - a, als b > a (Fig. 101) is het gelijk aan a - b, als a > b (Fig. 102), tenslotte is het nul als a = b.

Alle drie de gevallen vallen onder één formule:

b) Vergelijking | x + 3,2 | = 2 herschrijf in de vorm | x - (- 3.2) | \u003d 2 en verder (x, - 3.2) \u003d 2. Er zijn twee punten op de coördinaatlijn die zijn verwijderd van het punt - 3.2 op een afstand gelijk aan 2. Dit zijn punten - 5.2 en - 1.2 (Fig. . 104). Dus de vergelijking heeft twee wortel: -5,2 en -1,2.

№4.SET VAN ECHTE NUMMERS

De vereniging van de verzameling rationale getallen en de verzameling irrationele getallen wordt de verzameling genoemd Geldig (of materiaal ) nummers . De verzameling reële getallen wordt aangegeven met het symbool R. Blijkbaar, .

Echte getallen worden weergegeven op numerieke as Oh stippen (afb.). In dit geval komt elk reëel getal overeen met een bepaald punt van de numerieke as en komt elk punt van de as overeen met een bepaald reëel getal.

Daarom kun je in plaats van de woorden "reëel getal" "punt" zeggen.

Nummer 5. aantal gaten.

Type spleet	geometrische afbeeldingen	Aanwijzing	Schrijven met ongelijkheden
Interval

Halve interval
Halve interval


open straal
open straal

Nummer 6. Numerieke functie.

Laat een nummerreeks worden gegeven Als aan elk nummer een enkel nummer wordt toegewezen ja, dan zeggen we dat op de set D numeriek functie :

ja = f (x),

Een stelletje D genaamd functiebereik: en aangegeven D (f (x)). De verzameling van alle elementen f (x), waar heet functiebereik: en aangegeven E (f (x)).

Nummer x bel vaak functie argument of een onafhankelijke variabele, en het getal ja- afhankelijke variabele of, in feite, functie variabele x. Het nummer dat overeenkomt met de waarde wordt genoemd functiewaarde: op een punt en noem of

Een functie instellen: f, moet u specificeren:

1) het domein van de definitie D (f (x));

2) specificeer de regel f, volgens welke elke waarde wordt geassocieerd met een waarde ja = f (x).

№7. omgekeerde functie,

Omgekeerde functie

Als de rollen van argument en functie omgedraaid zijn, dan: x wordt een functie van ja. In dit geval spreekt men van een nieuwe functie genaamd omgekeerde functie. Stel we hebben een functie:

v = jij 2 ,

waar jij- argument, een v- functie. Als we hun rollen omdraaien, krijgen we jij als een functie v :

Als we het argument in beide functies aanduiden als x , en de functie door ja, dan hebben we twee functies:

waarvan elk het omgekeerde is van het andere.

VOORBEELDEN. Deze functies zijn omgekeerd aan elkaar:

1) zonde x en arcsin x, aangezien als ja= zonde x, dan x= Arcsin ja;

2) omdat x en Arccos x, aangezien als ja= cos x, dan x= Arccos ja;

3) tan x en Arctan x, aangezien als ja= tan x, dan x= Arctan ja;

4) e x en ln x, aangezien als ja= e x, dan x=ln j.

Inverse trigonometrische functies- wiskundige functies die omgekeerd zijn aan trigonometrische functies. Inverse trigonometrische functies omvatten meestal zes functies:

boogsinus(symbool: arcsin)

boog cosinus(symbool: arccos)

boog raaklijn(aanduiding: arctg; in buitenlandse literatuur arctan)

boog raaklijn(aanduiding: arcctg; in buitenlandse literatuur arccotan)

arcsecans(symbool: boogseconden)

arccosecant(aanduiding: arccosec; in buitenlandse literatuur arccsc)

№8. Basis elementaire functies. Elementaire functies

Het is vermeldenswaard dat de inverse trigonometrische functies meerwaardig zijn (oneindig significant), wanneer ze ermee werken, worden de zogenaamde hoofdwaarden gebruikt.

№9. Complexe getallen

worden geschreven als: een+ bi. Hier a en b – echte getallen, a i – denkbeeldige eenheid, d.w.z. i 2 = –1. Nummer a genaamd abscis, a b – ordinaat complex getal een+ bi. Twee complexe getallen een+ bi en a – bi genaamd conjugeren complexe getallen.

Reële getallen kunnen worden weergegeven door punten op een rechte lijn, zoals weergegeven in de afbeelding, waarbij punt A staat voor nummer 4 en punt B voor -5. Dezelfde nummers kunnen ook worden weergegeven door segmenten OA, OB, waarbij niet alleen rekening wordt gehouden met hun lengte, maar ook met hun richting.

Elk punt M van de getallenlijn geeft een reëel getal weer (rationeel als het segment OM vergelijkbaar is met een lengte-eenheid, en irrationeel als het incommensurabel is). Er is dus geen ruimte op de getallenlijn voor complexe getallen.

Maar complexe getallen kunnen worden weergegeven op het getallenvlak. Om dit te doen, kiezen we een rechthoekig coördinatensysteem op het vlak, met dezelfde schaal op beide assen.

Complex getal a + b ik weergegeven door het punt M, waarin de abscis x gelijk is aan de abscis a complex getal, en de ordinaat van y is gelijk aan de ordinaat b complex getal.

In dit artikel zullen we in detail analyseren: de absolute waarde van een getal. We geven verschillende definities van de modulus van een getal, introduceren notatie en geven grafische illustraties. In dit geval bekijken we verschillende voorbeelden van het per definitie vinden van de modulus van een getal. Daarna lijsten en rechtvaardigen we de belangrijkste eigenschappen van de module. Aan het einde van het artikel zullen we het hebben over hoe de modulus van een complex getal wordt bepaald en gevonden.

Paginanavigatie.

Modulus van getallen - definitie, notatie en voorbeelden

Eerst introduceren we modulus aanduiding. De module van het nummer a zal worden geschreven als , dat wil zeggen, links en rechts van het nummer zullen we verticale lijnen plaatsen die het teken van de module vormen. Laten we een paar voorbeelden geven. modulo -7 kan bijvoorbeeld worden geschreven als ; module 4.125 wordt geschreven als , en module wordt geschreven als .

De volgende definitie van de module verwijst naar, en daarom, naar, en naar gehele getallen, en naar rationale en irrationele getallen, wat betreft de samenstellende delen van de verzameling reële getallen. We zullen het hebben over de modulus van een complex getal in.

Definitie.

Modulus van a is ofwel het getal a zelf, als a een positief getal is, of het getal −a, het tegenovergestelde van het getal a, als a een negatief getal is, of 0, als a=0.

De stemhebbende definitie van de modulus van een getal wordt vaak in de volgende vorm geschreven: , betekent deze notatie dat als a>0 , als a=0 , en als a<0 .

Het record kan in een compactere vorm worden weergegeven . Deze notatie betekent dat als (a groter is dan of gelijk is aan 0 ), en als a<0 .

Er is ook een record . Hier moet het geval waarin a=0 afzonderlijk worden uitgelegd. In dit geval hebben we , maar −0=0 , aangezien nul wordt beschouwd als een getal dat tegengesteld is aan zichzelf.

Laten we brengen voorbeelden van het vinden van de modulus van een getal met een bepaalde definitie. Laten we bijvoorbeeld modules met nummers 15 en . Laten we beginnen met het vinden. Aangezien het getal 15 positief is, is de modulus ervan per definitie gelijk aan dit getal zelf, dat wil zeggen . Wat is de modulus van een getal? Aangezien het een negatief getal is, is de modulus gelijk aan het getal tegenover het getal, dat wil zeggen, het getal . Dus, .

Ter afsluiting van deze paragraaf geven we één conclusie, die erg handig is om in de praktijk toe te passen bij het vinden van de modulus van een getal. Uit de definitie van de modulus van een getal volgt dat de modulus van een getal is gelijk aan het getal onder het teken van de modulus, ongeacht het teken, en uit de hierboven besproken voorbeelden is dit heel duidelijk zichtbaar. De stemhebbende verklaring legt uit waarom de modulus van een getal ook wordt genoemd de absolute waarde van het getal. Dus de modulus van een getal en de absolute waarde van een getal zijn één en hetzelfde.

Modulus van een getal als afstand

Geometrisch kan de modulus van een getal worden geïnterpreteerd als: afstand. Laten we brengen bepaling van de modulus van een getal in termen van afstand.

Definitie.

Modulus van a is de afstand van de oorsprong op de coördinaatlijn tot het punt dat overeenkomt met het getal a.

Deze definitie komt overeen met de definitie van de modulus van een getal in de eerste alinea. Laten we dit punt uitleggen. De afstand van de oorsprong tot het punt dat overeenkomt met een positief getal is gelijk aan dit getal. Nul komt overeen met de oorsprong, dus de afstand van de oorsprong tot het punt met coördinaat 0 is nul (geen enkel segment en geen segment dat een fractie van het eenheidssegment vormt, moet worden uitgesteld om van punt O naar het punt te komen met coördinaat 0). De afstand van de oorsprong tot een punt met een negatieve coördinaat is gelijk aan het getal tegenover de coördinaat van het gegeven punt, aangezien het gelijk is aan de afstand van de oorsprong tot het punt waarvan de coördinaat het tegenovergestelde getal is.

De modulus van het getal 9 is bijvoorbeeld 9, aangezien de afstand van de oorsprong tot het punt met coördinaat 9 negen is. Laten we nog een voorbeeld nemen. Het punt met coördinaat −3.25 ligt op een afstand van 3.25 van punt O, dus .

De klinkende definitie van de modulus van een getal is een speciaal geval van het definiëren van de modulus van het verschil van twee getallen.

Definitie.

Verschilmodulus van twee getallen a en b is gelijk aan de afstand tussen de punten van de coördinaatlijn met coördinaten a en b .

Dat wil zeggen, als punten op de coördinaatlijn A(a) en B(b) worden gegeven, dan is de afstand van punt A naar punt B gelijk aan de modulus van het verschil tussen de getallen a en b. Als we punt O (referentiepunt) als punt B nemen, krijgen we de definitie van de modulus van het getal dat aan het begin van deze paragraaf is gegeven.

De modulus van een getal bepalen via de rekenkundige vierkantswortel

Soms gevonden bepaling van de modulus door de rekenkundige vierkantswortel.

Laten we bijvoorbeeld de modules van de getallen −30 berekenen op basis van deze definitie. We hebben . Op dezelfde manier berekenen we de modulus van tweederde: .

De definitie van de modulus van een getal in termen van de rekenkundige vierkantswortel komt ook overeen met de definitie in de eerste alinea van dit artikel. Laten we het laten zien. Laat a een positief getal zijn en laat −a negatief zijn. Dan en , als a=0 , dan .

Module-eigenschappen

De module heeft een aantal karakteristieke resultaten - module eigenschappen. Nu zullen we de belangrijkste en meest gebruikte ervan geven. Bij het onderbouwen van deze eigenschappen gaan we uit van de definitie van de modulus van een getal in termen van afstand.

Laten we beginnen met de meest voor de hand liggende module-eigenschap − modulus van een getal kan geen negatief getal zijn. In letterlijke vorm heeft deze eigenschap de vorm voor elk getal a . Deze eigenschap is heel gemakkelijk te rechtvaardigen: de modulus van een getal is de afstand en de afstand kan niet worden uitgedrukt als een negatief getal.

Laten we naar de volgende eigenschap van de module gaan. De modulus van een getal is gelijk aan nul als en slechts als dit getal nul is. De modulus van nul is per definitie nul. Nul komt overeen met de oorsprong, geen enkel ander punt op de coördinaatlijn komt overeen met nul, aangezien elk reëel getal wordt geassocieerd met een enkel punt op de coördinaatlijn. Om dezelfde reden komt elk ander getal dan nul overeen met een ander punt dan de oorsprong. En de afstand van de oorsprong tot een ander punt dan het punt O is niet gelijk aan nul, aangezien de afstand tussen twee punten gelijk is aan nul als en slechts als deze punten samenvallen. De bovenstaande redenering bewijst dat alleen de modulus van nul gelijk is aan nul.

Ga verder. Tegenoverliggende nummers hebben gelijke modules, dat wil zeggen, voor elk nummer a . Inderdaad, twee punten op de coördinatenlijn, waarvan de coördinaten tegengestelde getallen zijn, liggen op dezelfde afstand van de oorsprong, wat betekent dat de modules met tegengestelde getallen gelijk zijn.

De volgende module-eigenschap is: de modulus van het product van twee getallen is gelijk aan het product van de modules van deze getallen, d.w.z. . Per definitie is de modulus van het product van de getallen a en b ofwel a b als , of − (a b) als . Uit de regels voor vermenigvuldiging van reële getallen volgt dat het product van moduli van getallen a en b gelijk is aan ofwel a b , , of −(a b) , if , wat de beschouwde eigenschap bewijst.

De modulus van het quotiënt van het delen van a door b is gelijk aan het quotiënt van het delen van de modulus van a door de modulus van b, d.w.z. . Laten we deze eigenschap van de module rechtvaardigen. Aangezien het quotiënt gelijk is aan het product, dan is . Op grond van de vorige eigenschap hebben we: . Het blijft alleen om de gelijkheid te gebruiken, die geldig is vanwege de definitie van de modulus van het getal.

De volgende module-eigenschap wordt geschreven als een ongelijkheid: , a , b en c zijn willekeurige reële getallen. De geschreven ongelijkheid is niets meer dan Driehoeksongelijkheid. Om dit duidelijk te maken, nemen we de punten A(a) , B(b) , C(c) op de coördinaatlijn, en beschouwen we de gedegenereerde driehoek ABC, waarvan de hoekpunten op dezelfde lijn liggen. Per definitie is de modulus van het verschil gelijk aan de lengte van het segment AB, - de lengte van het segment AC, en - de lengte van het segment CB. Aangezien de lengte van een zijde van een driehoek niet groter is dan de som van de lengtes van de andere twee zijden, is de ongelijkheid , daarom geldt de ongelijkheid ook.

De zojuist bewezen ongelijkheid komt veel vaker voor in de vorm . De geschreven ongelijkheid wordt meestal beschouwd als een aparte eigenschap van de module met de formulering: “ De modulus van de som van twee getallen is niet groter dan de som van de moduli van deze getallen". Maar de ongelijkheid volgt direct uit de ongelijkheid , als we −b in plaats van b erin zetten, en c=0 nemen.

Complexe getalmodulus

Laten we het geven bepaling van de modulus van een complex getal. Laat ons gegeven worden complex getal, geschreven in algebraïsche vorm , waarbij x en y enkele reële getallen zijn, die respectievelijk de reële en denkbeeldige delen van een bepaald complex getal z vertegenwoordigen, en een denkbeeldige eenheid is.

Definitie.

De modulus van een complex getal z=x+i y wordt de rekenkundige vierkantswortel genoemd van de som van de kwadraten van de reële en imaginaire delen van een bepaald complex getal.

De modulus van een complex getal z wordt aangegeven als , dan kan de klinkende definitie van de modulus van een complex getal worden geschreven als .

Met deze definitie kunt u de modulus van elk complex getal in algebraïsche notatie berekenen. Laten we bijvoorbeeld de modulus van een complex getal berekenen. In dit voorbeeld is het reële deel van het complexe getal , en het denkbeeldige deel is min vier. Dan, door de definitie van de modulus van een complex getal, hebben we .

De geometrische interpretatie van de modulus van een complex getal kan worden gegeven in termen van afstand, naar analogie met de geometrische interpretatie van de modulus van een reëel getal.

Definitie.

Complexe getalmodulus z is de afstand van het begin van het complexe vlak tot het punt dat overeenkomt met het getal z in dit vlak.

Volgens de stelling van Pythagoras wordt de afstand van het punt O tot het punt met coördinaten (x, y) gevonden als , dus , waar . Daarom komt de laatste definitie van de modulus van een complex getal overeen met de eerste.

Met deze definitie kun je ook meteen aangeven wat de modulus van een complex getal z is, als het in goniometrische vorm is geschreven als of in exponentiële vorm. Hier . Bijvoorbeeld de modulus van een complex getal is 5 , en de modulus van het complexe getal is .

Het is ook te zien dat het product van een complex getal en zijn complexe geconjugeerde de som van de kwadraten van de reële en imaginaire delen geeft. Echt, . De resulterende gelijkheid stelt ons in staat om nog een definitie te geven van de modulus van een complex getal.

Definitie.

Complexe getalmodulus z is de rekenkundige vierkantswortel van het product van dit getal en zijn complexe geconjugeerde, dat wil zeggen .

Concluderend merken we op dat alle eigenschappen van de module die in de overeenkomstige subparagraaf zijn geformuleerd ook gelden voor complexe getallen.

Bibliografie.

Vilenkin N.Ya. enz. Wiskunde. Graad 6: leerboek voor onderwijsinstellingen.
Makarychev Yu.N., Mindyuk N.G., Neshkov K.I., Suvorova S.B. Algebra: leerboek voor 8 cellen. onderwijsinstellingen.
Lunts GL, Elsgolts LE. Functies van een complexe variabele: een leerboek voor universiteiten.
Privalov II Inleiding tot de theorie van functies van een complexe variabele.

We weten al dat de verzameling reële getallen $R$ wordt gevormd door rationale en irrationele getallen.

Rationele getallen kunnen altijd worden weergegeven als decimalen (eindig of oneindig periodiek).

Irrationele getallen worden geschreven als oneindige maar niet-recurrente decimalen.

De verzameling reële getallen $R$ bevat ook de elementen $-\infty $ en $+\infty $, waarvoor de ongelijkheden $-\infty

Overweeg manieren om reële getallen weer te geven.

Gemeenschappelijke breuken

Definitie

Een breuk wordt juist genoemd als de teller kleiner is dan de noemer. Omgekeerd wordt een breuk oneigenlijk genoemd als de teller groter is dan of gelijk is aan de noemer.

Voor gewone breuken zijn er eenvoudige, praktisch voor de hand liggende vergelijkingsregels ($m$,$n$,$p$ zijn natuurlijke getallen):

van twee breuken met dezelfde noemers, is die met de grotere teller groter, d.w.z. $\frac(m)(p) >\frac(n)(p) $ voor $m>n$;
van twee breuken met dezelfde tellers, is die met de kleinere noemer groter, d.w.z. $\frac(p)(m) >\frac(p)(n) $ voor $ m
een juiste breuk is altijd kleiner dan één; onjuiste breuk is altijd groter dan één; een breuk waarvan de teller gelijk is aan de noemer is gelijk aan één;
Elke oneigenlijke breuk is groter dan elke juiste breuk.

Decimale getallen

Definitie

voorbeeld 1

We bepalen de waarde van het decimale getal 3,74. We krijgen: $3,74=3+\frac(7)(10) +\frac(4)(100) $.

Het decimale getal kan worden afgerond. In dit geval moet u het cijfer opgeven waarop wordt afgerond.

De afrondingsregel is als volgt:

alle cijfers rechts van dit cijfer worden vervangen door nullen (als deze cijfers voor de komma staan) of worden weggegooid (als deze cijfers achter de komma staan);
als het eerste cijfer dat volgt op het gegeven cijfer kleiner is dan 5, wordt het cijfer van dit cijfer niet gewijzigd;
als het eerste cijfer dat volgt op het gegeven cijfer 5 of meer is, wordt het cijfer van dit cijfer met één verhoogd.

Voorbeeld 2

Laten we het getal 17302 afronden op het dichtstbijzijnde duizendtal: 17.000.
Laten we het getal 17378 afronden op het dichtstbijzijnde honderdtal: 17400.
Laten we het getal 17378,45 afronden op tientallen: 17380.
Laten we het getal 378.91434 afronden op het dichtstbijzijnde honderdtal: 378.91.
Laten we het getal 378.91534 afronden op het dichtstbijzijnde honderdtal: 378.92.

Een decimaal getal converteren naar een gewone breuk.

Zaak 1

Een decimaal getal is een einddecimaal.

De conversiemethode wordt getoond in het volgende voorbeeld.

Voorbeeld 2

We hebben: $3.74=3+\frac(7)(10) +\frac(4)(100) $.

Reduceer tot een gemeenschappelijke noemer en krijg:

De breuk kan worden verkleind: $3.74=\frac(374)(100) =\frac(187)(50) $.

Geval 2

Een decimaal getal is een oneindig terugkerend decimaal getal.

Voorbeeld 4

$0,\left(74\right)=\frac(74)(100) +\frac(74)(10000) +\frac(74)(1000000) +\ldots $. Het eerste lid van de progressie is $a=0.74$, de noemer van de progressie is $q=0.01$.

Voorbeeld 5

$0.5\left(8\right)=\frac(5)(10) +\frac(8)(100) +\frac(8)(1000) +\frac(8)(10000) +\ldots $ . Het eerste lid van de progressie is $a=0.08$, de noemer van de progressie is $q=0.1$.

Voorbeeld 6

Laten we de oneindige periodieke decimale breuk $0,\left(72\right)$ omzetten in een gewone.

Voorbeeld 7

Laten we de oneindige periodieke decimale breuk $0.5\left(3\right)$ omzetten in een gewone.

Het eerste lid van de progressie is $a=0.03$, de noemer van de progressie is $q=0.1$. We krijgen: $s=\frac(a)(1-q) =\frac(0.03)(1-0.1) =\frac(0.03)(0.9) =\frac(3)( 90) =\frac(1 )(30)$.

Dus $0.5\left(3\right)=\frac(5)(10) +\frac(1)(30) =\frac(5\cdot 3)(10\cdot 3) +\frac( 1)(30 ) =\frac(15)(30) +\frac(1)(30) =\frac(16)(30) =\frac(8)(15) $.

Reële getallen kunnen worden weergegeven door punten op de getallenlijn.

In dit geval noemen we de numerieke as een oneindige lijn waarop de oorsprong (punt $O$), positieve richting (aangegeven door een pijl) en schaal (om waarden weer te geven) zijn geselecteerd.

Interval $\links(a,\;b\rechts)$. Tegelijkertijd $ a
Segment $\left$. Bovendien, $a\le x\le b$.
Halve segmenten of halve intervallen $\left$. Tegelijkertijd $ a \le x
Oneindige overspanningen, bijv. $a

De absolute waarde van het getal

Geometrisch betekent $\left|x\right|$ de afstand tussen de punten $x$ en 0 op de reële as.

Eigenschappen van absolute waarden:

uit de definitie volgt dat $\left|x\right|\ge 0$, $\left|x\right|=\left|-x\right|$;
voor de modulus van de som en voor de modulus van het verschil van twee getallen, de ongelijkheden $\left|x+y\right|\le \left|x\right|+\left|y\right|$, $\ left|x-y\right|\le \left|x\right|+\left|y\right|$ en ook $\left|x+y\right|\ge \left|x\right|-\left|y \right|$,$\ left|x-y\right|\ge \left|x\right|-\left|y\right|$;
de modulus van het product en de modulus van het quotiënt van twee getallen voldoen aan de gelijkheden $\left|x\cdot y\right|=\left|x\right|\cdot \left|y\right|$ en $\left |\frac(x)( y) \right|=\frac(\left|x\right|)(\left|y\right|) $.

Op basis van de definitie van de absolute waarde voor een willekeurig getal $a>0$ kan men ook de gelijkwaardigheid van de volgende ongelijkhedenparen vaststellen:

als $ \links|x\rechts|
als $\left|x\right|\le a$ dan $-a\le x\le a$;
als $\left|x\right|>a$ dan ofwel $xa$;
als $\left|x\right|\ge a$, dan $x\le -a$ of $x\ge a$.

Voorbeeld 8

Los de ongelijkheid $\left|2\cdot x+1\right| . op

Deze ongelijkheid is gelijk aan de ongelijkheid $-7

Vanaf hier krijgen we: $ -8