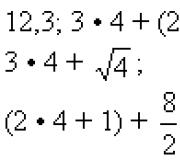Penggambaran bilangan asli dengan titik-titik pada garis bilangan. Modulus bilangan (nilai mutlak bilangan), definisi, contoh, sifat
Kita telah mengetahui bahwa himpunan bilangan real $R$ dibentuk oleh bilangan rasional dan irasional.
Bilangan rasional selalu dapat direpresentasikan sebagai desimal (periodik terbatas atau tak terbatas).
Bilangan irasional ditulis sebagai desimal tak terbatas tetapi tidak berulang.
Himpunan bilangan real $R$ juga mencakup elemen $-\infty $ dan $+\infty $, yang pertidaksamaannya $-\infty
Pertimbangkan cara untuk mewakili bilangan real.
pecahan biasa
Pecahan biasa ditulis menggunakan dua bilangan asli dan batang pecahan horizontal. Bilah pecahan sebenarnya menggantikan tanda pembagian. Bilangan di bawah garis adalah penyebut (pembagi), bilangan di atas garis adalah pembilangnya (dibagi).
Definisi
Suatu pecahan disebut wajar jika pembilangnya lebih kecil dari penyebutnya. Sebaliknya, suatu pecahan disebut tidak wajar jika pembilangnya lebih besar atau sama dengan penyebutnya.
Untuk pecahan biasa, ada aturan perbandingan sederhana, praktis jelas ($m$,$n$,$p$ adalah bilangan asli):
- dari dua pecahan dengan penyebut yang sama, pecahan dengan pembilang yang lebih besar lebih besar, yaitu $\frac(m)(p) >\frac(n)(p) $ for $m>n$;
- dari dua pecahan dengan pembilang yang sama, pecahan dengan penyebut yang lebih kecil lebih besar, yaitu $\frac(p)(m) >\frac(p)(n) $ untuk $ m
- pecahan biasa selalu kurang dari satu; pecahan tak wajar selalu lebih besar dari satu; pecahan yang pembilangnya sama dengan penyebutnya sama dengan satu;
- Setiap pecahan tidak wajar lebih besar dari pecahan biasa mana pun.
Bilangan desimal
Notasi bilangan desimal (pecahan desimal) memiliki bentuk: bagian bilangan bulat, titik desimal, bagian pecahan. Notasi desimal dari pecahan biasa dapat diperoleh dengan membagi "sudut" pembilang dengan penyebut. Ini dapat menghasilkan pecahan desimal terbatas atau pecahan desimal periodik tak terbatas.
Definisi
Angka pecahan disebut tempat desimal. Dalam hal ini, digit pertama setelah koma disebut digit persepuluh, digit kedua - seperseratus, digit ketiga - seperseribu, dll.
Contoh 1
Kami menentukan nilai angka desimal 3,74. Kami mendapatkan: $3,74=3+\frac(7)(10) +\frac(4)(100) $.
Bilangan desimal dapat dibulatkan. Dalam hal ini, Anda harus menentukan digit yang akan dilakukan pembulatan.
Aturan pembulatannya adalah sebagai berikut:
- semua angka di sebelah kanan angka ini diganti dengan nol (jika angka-angka ini sebelum titik desimal) atau dibuang (jika angka-angka ini berada setelah titik desimal);
- jika digit pertama setelah digit yang diberikan kurang dari 5, maka digit digit ini tidak diubah;
- jika angka pertama setelah angka yang diberikan adalah 5 atau lebih, maka angka dari angka ini ditambah satu.
Contoh 2
- Mari kita bulatkan angka 17302 ke ribuan terdekat: 17000.
- Mari kita bulatkan angka 17378 ke ratusan terdekat: 17400.
- Mari kita bulatkan angka 17378,45 menjadi puluhan: 17380.
- Mari kita bulatkan angka 378.91434 ke perseratus terdekat: 378.91.
- Mari kita bulatkan angka 378.91534 ke perseratus terdekat: 378.92.
Mengubah bilangan desimal menjadi pecahan biasa.
Kasus 1
Bilangan desimal adalah desimal berakhir.
Metode konversi ditunjukkan dalam contoh berikut.
Contoh 2
Kami memiliki: $3,74=3+\frac(7)(10) +\frac(4)(100) $.
Kurangi menjadi penyebut yang sama dan dapatkan:
Pecahan dapat dikurangi: $3,74=\frac(374)(100) =\frac(187)(50) $.
Kasus 2
Bilangan desimal adalah desimal berulang yang tak terbatas.
Metode transformasi didasarkan pada kenyataan bahwa bagian periodik dari pecahan desimal periodik dapat dianggap sebagai jumlah anggota deret geometri menurun tak terbatas.
Contoh 4
$0,\kiri(74\kanan)=\frac(74)(100) +\frac(74)(10000) +\frac(74)(1000000) +\ldots $. Anggota pertama dari progres adalah $a=0.74$, penyebut dari progresi adalah $q=0.01$.
Contoh 5
$0,5\kiri(8\kanan)=\frac(5)(10) +\frac(8)(100) +\frac(8)(1000) +\frac(8)(10000) +\ldots $ . Anggota pertama dari kemajuan adalah $a=0,08$, penyebut dari kemajuan adalah $q=0,1$.
Jumlah suku-suku barisan geometri menurun tak hingga dihitung dengan rumus $s=\frac(a)(1-q) $, dengan $a$ suku pertama dan $q$ penyebut barisan $ \kiri (0
Contoh 6
Mari kita ubah pecahan desimal periodik tak hingga $0,\left(72\right)$ menjadi pecahan biasa.
Anggota pertama dari progres adalah $a=0.72$, penyebut dari progresi adalah $q=0.01$. Kita peroleh: $s=\frac(a)(1-q) =\frac(0.72)(1-0.01) =\frac(0.72)(0.99) =\frac(72)( 99) =\frac(8 )(11)$. Jadi $0,\kiri(72\kanan)=\frac(8)(11) $.
Contoh 7
Mari kita ubah pecahan desimal periodik tak hingga $0,5\kiri(3\kanan)$ menjadi pecahan biasa.
Anggota pertama dari progres adalah $a=0.03$, penyebut dari progres adalah $q=0.1$. Kita peroleh: $s=\frac(a)(1-q) =\frac(0.03)(1-0.1) =\frac(0.03)(0.9) =\frac(3)( 90) =\frac(1 )(30)$.
Jadi $0,5\kiri(3\kanan)=\frac(5)(10) +\frac(1)(30) =\frac(5\cdot 3)(10\cdot 3) +\frac( 1)(30 ) =\frac(15)(30) +\frac(1)(30) =\frac(16)(30) =\frac(8)(15) $.
Bilangan real dapat diwakili oleh titik-titik pada garis bilangan.
Dalam hal ini, kami menyebut sumbu numerik sebagai garis tak hingga di mana titik asal (titik $O$), arah positif (ditunjukkan oleh panah) dan skala (untuk menampilkan nilai) dipilih.
Antara semua bilangan real dan semua titik sumbu numerik ada korespondensi satu-satu: setiap titik sesuai dengan satu angka dan, sebaliknya, setiap angka sesuai dengan satu titik. Oleh karena itu, himpunan bilangan real kontinu dan tak terbatas dengan cara yang sama seperti sumbu bilangan kontinu dan tak terbatas.
Beberapa himpunan bagian dari himpunan bilangan real disebut interval numerik. Unsur-unsur interval numerik adalah bilangan $x\dalam R$ yang memenuhi pertidaksamaan tertentu. Biarkan $a\di R$, $b\di R$ dan $a\le b$. Dalam hal ini, jenis kesenjangan dapat sebagai berikut:
- Interval $\kiri(a,\; b\kanan)$. Pada saat yang sama $a
- Segmen $\kiri$. Selain itu, $a\le x\le b$.
- Setengah-segmen atau setengah-interval $\left$. Pada saat yang sama $a \le x
- Rentang tak terbatas, misalnya $a
Sangat penting juga semacam interval, yang disebut lingkungan suatu titik. Lingkungan dari titik tertentu $x_(0) \in R$ adalah interval arbitrer $\left(a,\; b\right)$ yang berisi titik ini di dalam dirinya sendiri, yaitu $a 0$ - radius 10.
Nilai mutlak dari bilangan
Nilai mutlak (atau modulus) dari bilangan real $x$ adalah bilangan real non-negatif $\left|x\right|$, didefinisikan oleh rumus: $\left|x\right|=\left\(\ mulai(array)(c) (\; \; x\; \; (\rm aktif)\; \; x\ge 0) \\ (-x\; \; (\rm aktif)\; \; x
Secara geometris, $\left|x\right|$ berarti jarak antara titik $x$ dan 0 pada sumbu nyata.
Sifat nilai mutlak:
- berikut dari definisi bahwa $\left|x\right|\ge 0$, $\left|x\right|=\left|-x\right|$;
- untuk modulus penjumlahan dan modulus selisih dua bilangan, pertidaksamaan $\left|x+y\right|\le \left|x\right|+\left|y\right|$, $\ kiri|x-y\kanan|\le \kiri|x\kanan|+\kiri|y\kanan|$ dan juga $\kiri|x+y\kanan|\ge \kiri|x\kanan|-\kiri|y \kanan|$,$\ kiri|x-y\kanan|\ge \kiri|x\kanan|-\kiri|y\kanan|$;
- modulus hasil kali dan modulus hasil bagi dua bilangan memenuhi persamaan $\left|x\cdot y\right|=\left|x\right|\cdot \left|y\right|$ dan $\left |\frac(x)( y) \kanan|=\frac(\kiri|x\kanan|)(\kiri|y\kanan|) $.
Berdasarkan definisi nilai mutlak untuk bilangan arbitrer $a>0$, kita juga dapat menetapkan ekivalensi dari pasangan pertidaksamaan berikut:
- jika $ \kiri|x\kanan|
- jika $\left|x\right|\le a$ maka $-a\le x\le a$;
- jika $\left|x\right|>a$ maka $xa$;
- jika $\left|x\right|\ge a$, maka $x\le -a$ atau $x\ge a$.
Contoh 8
Selesaikan pertidaksamaan $\left|2\cdot x+1\right|
Pertidaksamaan ini setara dengan pertidaksamaan $-7
Dari sini kita mendapatkan: $-8
Garis bilangan, sumbu bilangan, adalah garis yang menggambarkan bilangan real. Pada garis lurus, titik asal dipilih - titik O (titik O mewakili 0) dan titik L, mewakili unit. Titik L biasanya berdiri di sebelah kanan titik O. Segmen OL disebut segmen satuan.
Titik di sebelah kanan titik O menunjukkan bilangan positif. Titik di sebelah kiri titik. Oh, gambarkan angka negatif. Jika titik X mewakili bilangan positif x, maka jarak OX = x. Jika titik X mewakili bilangan negatif x, maka jarak OX = - x.
Bilangan yang menunjukkan posisi suatu titik pada garis lurus disebut koordinat titik tersebut.
Titik V pada gambar memiliki koordinat 2, dan titik H memiliki koordinat -2,6.
Modulus bilangan real adalah jarak dari titik asal ke titik yang bersesuaian dengan bilangan tersebut. Tentukan modulus dari bilangan x, sehingga: | x |. Jelas, | 0 | = 0.
Jika bilangan x lebih besar dari 0, maka | x | = x, dan jika x lebih kecil dari 0, maka | x | = -x. Pada properti modul ini, solusi dari banyak persamaan dan pertidaksamaan dengan modul didasarkan.
Contoh: Selesaikan Persamaan | x - 3 | = 1.
Solusi: Pertimbangkan dua kasus - kasus pertama, ketika x -3 > 0, dan kasus kedua, ketika x - 3 0.
1. x - 3 > 0, x > 3.
Dalam hal ini | x - 3 | = x - 3.
Persamaan mengambil bentuk x - 3 \u003d 1, x \u003d 4. 4\u003e 3 - memenuhi kondisi pertama.
2. x -3 0, x 3.
Dalam hal ini | x - 3 | = - x + 3
Persamaan mengambil bentuk x + 3 \u003d 1, x \u003d - 2. -2 3 - memenuhi kondisi kedua.
Jawaban: x = 4, x = -2.
Ekspresi numerik.
Ekspresi numerik adalah kumpulan dari satu atau lebih angka dan fungsi yang dihubungkan oleh operator aritmatika dan tanda kurung.
Contoh ekspresi numerik: 
Nilai ekspresi numerik adalah angka.
Operasi dalam ekspresi numerik dilakukan dalam urutan berikut:
1. Tindakan dalam tanda kurung.
2. Perhitungan fungsi.
3. Eksponen
4. Perkalian dan pembagian.
5. Penambahan dan pengurangan.
6. Operasi dengan tipe yang sama dilakukan dari kiri ke kanan.
Jadi nilai dari ekspresi pertama adalah bilangan itu sendiri 12,3
Untuk menghitung nilai ekspresi kedua, kami akan melakukan tindakan dalam urutan berikut:
1. Lakukan tindakan dalam tanda kurung dalam urutan berikut - pertama kita naikkan 2 ke pangkat ketiga, lalu kurangi 11 dari angka yang dihasilkan:
3 4 + (23 - 11) = 3 4 + (8 - 11) = 3 4 + (-3)
2. Kalikan 3 dengan 4:
3 4 + (-3) = 12 + (-3)
3. Lakukan operasi secara berurutan dari kiri ke kanan:
12 + (-3) = 9.
Ekspresi dengan variabel adalah kumpulan dari satu atau lebih angka, variabel, dan fungsi yang dihubungkan oleh operator aritmatika dan tanda kurung. Nilai ekspresi dengan variabel tergantung pada nilai variabel yang termasuk di dalamnya. Urutan operasi di sini sama dengan ekspresi numerik. Terkadang berguna untuk menyederhanakan ekspresi dengan variabel dengan melakukan berbagai tindakan - kurung, ekspansi kurung, pengelompokan, pengurangan pecahan, pengurangan yang serupa, dll. Juga, untuk menyederhanakan ekspresi, berbagai rumus sering digunakan, misalnya, rumus perkalian yang disingkat, sifat berbagai fungsi, dll.
Ekspresi aljabar.
Ekspresi aljabar adalah satu atau lebih besaran aljabar (angka dan huruf) yang saling berhubungan dengan tanda-tanda operasi aljabar: penambahan, pengurangan, perkalian dan pembagian, serta mengekstraksi akar dan menaikkan pangkat bilangan bulat (selain itu, akar dan eksponen harus selalu menjadi bilangan bulat) dan tanda-tanda urutan tindakan ini (biasanya berbagai jenis kurung). Jumlah nilai yang termasuk dalam ekspresi aljabar harus terbatas.
Contoh ekspresi aljabar:
"Ekspresi aljabar" adalah konsep sintaksis, yaitu, sesuatu adalah ekspresi aljabar jika dan hanya jika mematuhi aturan tata bahasa tertentu (lihat Tata bahasa formal). Jika huruf-huruf dalam ekspresi aljabar dianggap variabel, maka ekspresi aljabar memperoleh arti dari fungsi aljabar.
nomor 1. Sifat-sifat bilangan rasional.
ketertiban . Untuk setiap bilangan rasional dan ada aturan yang memungkinkan Anda untuk secara unik mengidentifikasi di antara mereka satu dan hanya satu dari tiga hubungan: "", "" atau "". Aturan ini disebut aturan pemesanan dan dirumuskan sebagai berikut: dua bilangan positif dihubungkan oleh relasi yang sama sebagai dua bilangan bulat; dua bilangan non-positif dan terkait dengan hubungan yang sama seperti dua bilangan non-negatif dan; jika tiba-tiba tidak negatif, tetapi negatif, maka.
penjumlahan pecahan
Operasi penambahan
.
aturan penjumlahan, yang menempatkan mereka dalam korespondensi dengan beberapa bilangan rasional . Dalam hal ini, nomor itu sendiri disebut jumlah
angka u dilambangkan, dan proses menemukan angka seperti itu disebut penjumlahan. Aturan penjumlahan memiliki bentuk sebagai berikut: 
.
operasi perkalian
.
Untuk setiap bilangan rasional dan ada yang disebut aturan perkalian, yang menempatkan mereka dalam korespondensi dengan beberapa bilangan rasional . Dalam hal ini, nomor itu sendiri disebut kerja
angka ii dilambangkan, dan proses menemukan angka seperti itu juga disebut perkalian. Aturan perkaliannya adalah sebagai berikut: 
.
Transitivitas hubungan pesanan. Untuk setiap rangkap tiga bilangan rasional , dan jika lebih kecil dan lebih kecil, maka lebih sedikit, dan jika sama dan sama, maka sama.
komutatifitas tambahan. Dari perubahan tempat istilah rasional, jumlahnya tidak berubah.
Keterkaitan tambahan. Urutan penambahan tiga bilangan rasional tidak mempengaruhi hasil.
Ketersediaannol . Ada bilangan rasional 0 yang mempertahankan setiap bilangan rasional lainnya ketika dijumlahkan.
Kehadiran angka yang berlawanan. Setiap bilangan rasional memiliki bilangan rasional yang berlawanan, yang jika dijumlahkan menghasilkan 0.
Komutatifitas perkalian. Dengan mengubah tempat faktor rasional, produk tidak berubah.
Asosiatif perkalian. Urutan perkalian tiga bilangan rasional tidak mempengaruhi hasil.
Ketersediaanunit . Ada bilangan rasional 1 yang mempertahankan setiap bilangan rasional lainnya ketika dikalikan.
Ketersediaanangka timbal balik . Setiap bilangan rasional bukan nol memiliki bilangan rasional terbalik, perkalian dengan yang memberikan 1.
distribusi perkalian terhadap penjumlahan. Operasi perkalian konsisten dengan operasi penjumlahan melalui hukum distribusi:
Koneksi relasi order dengan operasi penjumlahan. Bilangan rasional yang sama dapat ditambahkan ke ruas kiri dan kanan pertidaksamaan rasional.
Koneksi relasi orde dengan operasi perkalian. Ruas kiri dan kanan pertidaksamaan rasional dapat dikalikan dengan bilangan rasional positif yang sama.
Aksioma Archimedes . Berapa pun bilangan rasional , Anda dapat mengambil begitu banyak unit sehingga jumlahnya akan melebihi.
2. Modulus bilangan real.
Definisi . Modulus bilangan real non-negatif x adalah bilangan itu sendiri: | x | = x; modulus bilangan real negatif x adalah kebalikannya: I x | = -x.
Singkatnya, tertulis seperti ini:
2. Arti geometris dari modulus bilangan real
Mari kita kembali ke himpunan R bilangan real dan geometriknya model- nomor baris. Kami menandai dua titik a dan b pada garis (dua bilangan real a dan b), dilambangkan dengan (a, b) jarak antara titik a dan b (- huruf alfabet Yunani "ro"). Jarak ini sama dengan b - a, jika b > a (Gbr. 101), sama dengan a - b, jika a > b (Gbr. 102), akhirnya nol jika a = b.
Ketiga kasus tersebut dicakup oleh satu formula:
b) Persamaan | x + 3.2 | = 2 tulis ulang dalam bentuk | x - (- 3.2) | \u003d 2 dan selanjutnya (x, - 3.2) \u003d 2. Ada dua titik pada garis koordinat yang dihilangkan dari titik - 3.2 pada jarak yang sama dengan 2. Ini adalah titik - 5.2 dan - 1.2 (Gbr. . 104). Jadi persamaan memiliki dua akar: -5.2 dan -1.2.
№4.SET ANGKA NYATA
Gabungan himpunan bilangan rasional dan himpunan bilangan irasional disebut himpunan sah (atau bahan ) angka . Himpunan bilangan real dilambangkan dengan simbol R. Jelas sekali, .
Bilangan real ditampilkan di sumbu numerik
Oh titik (Gbr.). 
Dalam hal ini, setiap bilangan real sesuai dengan titik tertentu dari sumbu numerik, dan setiap titik sumbu sesuai dengan bilangan real tertentu.
Oleh karena itu, alih-alih kata "bilangan asli" Anda bisa mengatakan "titik".
Nomor 5. kesenjangan angka.
|
Jenis celah |
gambar geometris |
Penamaan |
Menulis menggunakan pertidaksamaan |
|
Selang |
| ||
|
| |||
|
Setengah interval |
| ||
|
Setengah interval |
| ||
|
| |||
|
| |||
|
balok terbuka |
| ||
|
balok terbuka |
|
6. Fungsi numerik.
Biarkan himpunan nomor diberikan Jika setiap nomor diberikan nomor tunggal kamu, maka kami mengatakan itu di lokasi syuting D numerik fungsi :
|
kamu = f (x), |
Sekelompok D ditelepon lingkup fungsi dan dilambangkan D (f (x)). Himpunan semua elemen f (x), di mana disebut rentang fungsi dan dilambangkan E (f (x)).
Nomor x sering menelepon argumen fungsi atau variabel bebas, dan bilangan kamu- variabel terikat atau, pada kenyataannya, fungsi variabel x. Bilangan yang sesuai dengan nilainya disebut nilai fungsi pada suatu titik dan menyatakan atau
Untuk mengatur fungsi f, Anda perlu menentukan:
1) domain definisinya D (f (x));
2) tentukan aturannya f, yang menurutnya setiap nilai dikaitkan dengan beberapa nilai kamu = f (x).
№7. fungsi terbalik,
Fungsi terbalik
Jika peran argumen dan fungsi dibalik, maka x menjadi fungsi dari kamu. Dalam hal ini, seseorang berbicara tentang fungsi baru yang disebut fungsi terbalik. Misalkan kita memiliki fungsi:
v = kamu 2 ,
di mana kamu- argumen, a v- fungsi. Jika kita membalikkan peran mereka, kita mendapatkan kamu sebagai fungsi v :
Jika kita menyatakan argumen di kedua fungsi sebagai x , dan fungsi melalui kamu, maka kita memiliki dua fungsi:
yang masing-masing merupakan kebalikan dari yang lain.
CONTOH. Fungsi-fungsi ini saling terbalik:
1) dosa x dan arcsin x, karena jika kamu= dosa x, kemudian x= Arcsin kamu;
2) karena x dan Arccos x, karena jika kamu= cos x, kemudian x= Arcos kamu;
3) tan x dan Arctan x, karena jika kamu= tan x, kemudian x= Arctan kamu;
4) e x dan ln x, karena jika kamu= e x, kemudian x= ln y.
Fungsi trigonometri terbalik- fungsi matematika yang kebalikan dari fungsi trigonometri. Fungsi trigonometri terbalik biasanya mencakup enam fungsi:
arcsinus(simbol: arcsin)
busur kosinus(simbol: arccos)
tangen busur(sebutan: arctg; dalam sastra asing arctan)
tangen busur(sebutan: arcctg; dalam literatur asing arccotan)
busur panah(simbol: arcsec)
arccosecant(sebutan: arccosec; dalam literatur asing arccsc)
№8. Fungsi dasar dasar. Fungsi Dasar
Perlu dicatat bahwa fungsi trigonometri terbalik adalah multi-nilai (sangat signifikan), ketika beroperasi dengannya, apa yang disebut nilai utama digunakan.
№9. Bilangan kompleks
ditulis sebagai: a+ dua. Di Sini sebuah dan b – bilangan asli, sebuah saya – satuan imajiner, yaitu saya 2 = –1. Nomor sebuah ditelepon absis, sebuah b – ordinat bilangan kompleks a+ dua. Dua bilangan kompleks a+ dua dan sebuah – dua ditelepon mengkonjugasikan bilangan kompleks.
Bilangan real dapat diwakili oleh titik-titik pada garis lurus, seperti yang ditunjukkan pada gambar, di mana titik A mewakili angka 4, dan titik B mewakili -5. Angka yang sama juga dapat diwakili oleh segmen OA, OB, dengan mempertimbangkan tidak hanya panjangnya, tetapi juga arahnya.
Setiap titik M dari garis bilangan menggambarkan suatu bilangan real (rasional jika segmen OM sebanding dengan satuan panjang, dan irasional jika tidak dapat dibandingkan). Jadi, tidak ada ruang pada garis bilangan untuk bilangan kompleks.
Tetapi bilangan kompleks dapat direpresentasikan pada bidang bilangan. Untuk melakukan ini, kami memilih sistem koordinat persegi panjang pada bidang, dengan skala yang sama pada kedua sumbu.
Bilangan kompleks a + b saya diwakili oleh titik M, di mana absis x sama dengan absis sebuah bilangan kompleks, dan ordinat y sama dengan ordinat b bilangan kompleks.
Pada artikel ini, kami akan menganalisis secara rinci nilai mutlak suatu bilangan. Kami akan memberikan berbagai definisi modulus suatu bilangan, memperkenalkan notasi dan memberikan ilustrasi grafis. Dalam hal ini, kami mempertimbangkan berbagai contoh untuk menemukan modulus suatu bilangan menurut definisi. Setelah itu, kami membuat daftar dan membenarkan properti utama modul. Di akhir artikel, kita akan berbicara tentang bagaimana modulus bilangan kompleks ditentukan dan ditemukan.
Navigasi halaman.
Modulus bilangan - definisi, notasi dan contoh
Pertama kami perkenalkan penunjukan modulus. Modul angka a akan dituliskan , yaitu di sebelah kiri dan di sebelah kanan angka tersebut akan dibuat garis vertikal yang membentuk tanda modul tersebut. Mari kita berikan beberapa contoh. Misalnya, modulo -7 dapat ditulis sebagai ; modul 4,125 ditulis sebagai , dan modul ditulis sebagai .
Definisi modul berikut mengacu pada, dan oleh karena itu, ke, dan ke bilangan bulat, dan ke bilangan rasional dan irasional, sebagai bagian penyusun himpunan bilangan real. Kita akan berbicara tentang modulus bilangan kompleks di.
Definisi.
Modul dari adalah bilangan a itu sendiri, jika a bilangan positif, atau bilangan a, kebalikan dari bilangan a, jika a bilangan negatif, atau 0, jika a=0.
Definisi modulus bilangan yang disuarakan sering ditulis dalam bentuk berikut: 
, notasi ini berarti bahwa jika a>0 , jika a=0 , dan jika a<0
.
Catatan dapat direpresentasikan dalam bentuk yang lebih ringkas 
. Notasi ini berarti bahwa jika (a lebih besar atau sama dengan 0 ), dan jika a<0
.
Ada juga rekornya 
. Di sini, kasus ketika a=0 harus dijelaskan secara terpisah. Dalam hal ini, kita memiliki , tetapi 0=0 , karena nol dianggap sebagai bilangan yang berlawanan dengan dirinya sendiri.
Ayo bawa contoh mencari modulus bilangan dengan definisi yang diberikan. Sebagai contoh, mari kita cari modul angka 15 dan . Mari kita mulai dengan menemukan . Karena angka 15 positif, modulusnya, menurut definisi, sama dengan angka ini sendiri, yaitu . Apa modulus suatu bilangan? Karena merupakan bilangan negatif, maka modulusnya sama dengan bilangan yang berlawanan dengan bilangan tersebut, yaitu bilangan 
. Dengan demikian, .
Sebagai kesimpulan dari paragraf ini, kami memberikan satu kesimpulan, yang sangat nyaman untuk diterapkan dalam praktik ketika menemukan modulus suatu bilangan. Dari definisi modulus suatu bilangan, maka: modulus angka sama dengan angka di bawah tanda modulus, terlepas dari tandanya, dan dari contoh-contoh yang dibahas di atas, ini terlihat sangat jelas. Pernyataan bersuara menjelaskan mengapa modulus suatu bilangan disebut juga nilai mutlak bilangan tersebut. Jadi modulus suatu bilangan dan nilai mutlak suatu bilangan adalah satu dan sama.
Modulus bilangan sebagai jarak
Secara geometris, modulus suatu bilangan dapat diartikan sebagai jarak. Ayo bawa penentuan modulus angka dalam hal jarak.
Definisi.
Modul dari adalah jarak dari titik asal pada garis koordinat ke titik yang bersesuaian dengan bilangan a.
Definisi ini konsisten dengan definisi modulus bilangan yang diberikan pada paragraf pertama. Mari kita jelaskan poin ini. Jarak dari titik asal ke titik yang bersesuaian dengan bilangan positif sama dengan bilangan ini. Nol sesuai dengan titik asal, sehingga jarak dari titik asal ke titik dengan koordinat 0 adalah nol (tidak ada segmen tunggal dan tidak ada segmen yang membentuk pecahan dari segmen unit perlu ditunda untuk mendapatkan dari titik O ke titik dengan koordinat 0). Jarak dari titik asal ke titik dengan koordinat negatif sama dengan angka yang berlawanan dengan koordinat titik yang diberikan, karena sama dengan jarak dari titik asal ke titik yang koordinatnya berlawanan dengan angka.
Misalnya modulus bilangan 9 adalah 9, karena jarak dari titik asal ke titik dengan koordinat 9 adalah sembilan. Mari kita ambil contoh lain. Titik dengan koordinat 3,25 berada pada jarak 3,25 dari titik O, jadi 
.
Definisi modulus bilangan yang dibunyikan adalah kasus khusus untuk mendefinisikan modulus selisih dua bilangan.
Definisi.
Modulus selisih dua bilangan a dan b sama dengan jarak antara titik-titik pada garis koordinat dengan koordinat a dan b .
Artinya, jika diberikan titik-titik pada garis koordinat A(a) dan B(b), maka jarak titik A ke titik B sama dengan modulus selisih angka a dan b. Jika kita mengambil titik O (titik acuan) sebagai titik B, maka kita akan mendapatkan definisi modulus dari bilangan yang diberikan di awal paragraf ini.
Menentukan modulus suatu bilangan melalui akar kuadrat aritmatika
Kadang-kadang ditemukan penentuan modulus melalui akar kuadrat aritmatika.
Misalnya, mari kita hitung modul angka 30 dan berdasarkan definisi ini. Kita punya . Demikian pula, kami menghitung modulus dua pertiga: 
.
Definisi modulus suatu bilangan dalam akar kuadrat aritmatika juga konsisten dengan definisi yang diberikan dalam paragraf pertama artikel ini. Mari kita tunjukkan. Biarkan a menjadi bilangan positif, dan biarkan a menjadi negatif. Kemudian 
dan 
, jika a=0 , maka 
.
Properti Modul
Modul ini memiliki sejumlah hasil karakteristik - properti modul. Sekarang kami akan memberikan yang utama dan paling umum digunakan. Saat membuktikan sifat-sifat ini, kita akan mengandalkan definisi modulus bilangan dalam hal jarak.
Mari kita mulai dengan properti modul yang paling jelas modulus suatu bilangan tidak boleh berupa bilangan negatif. Dalam bentuk literal, properti ini memiliki bentuk untuk sembarang bilangan a . Sifat ini sangat mudah untuk dibenarkan: modulus suatu bilangan adalah jarak, dan jarak tidak dapat dinyatakan sebagai bilangan negatif.
Mari kita beralih ke properti modul berikutnya. Modulus suatu bilangan sama dengan nol jika dan hanya jika bilangan tersebut adalah nol. Modulus nol adalah nol menurut definisi. Nol sesuai dengan asal, tidak ada titik lain pada garis koordinat yang sesuai dengan nol, karena setiap bilangan real dikaitkan dengan satu titik pada garis koordinat. Untuk alasan yang sama, angka apa pun selain nol sesuai dengan titik selain titik asal. Dan jarak dari titik asal ke sembarang titik selain titik O tidak sama dengan nol, karena jarak antara dua titik sama dengan nol jika dan hanya jika titik-titik ini bertepatan. Alasan di atas membuktikan bahwa hanya modulus nol yang sama dengan nol.
Pindah. Angka yang berlawanan memiliki modul yang sama, yaitu untuk angka apa pun a . Memang, dua titik pada garis koordinat, yang koordinatnya adalah angka yang berlawanan, berada pada jarak yang sama dari titik asal, yang berarti modul dari angka yang berlawanan adalah sama.
Properti modul berikutnya adalah: modulus produk dari dua angka sama dengan produk dari modul dari angka-angka ini, yaitu, . Menurut definisi, modulus hasil kali bilangan a dan b adalah a b jika , atau (a b) jika . Ini mengikuti dari aturan perkalian bilangan real bahwa produk modulus bilangan a dan b sama dengan a b , , atau (a b) , jika , yang membuktikan properti yang dipertimbangkan.
Modulus hasil bagi pembagian a dengan b sama dengan hasil bagi pembagian modulus a dengan modulus b, yaitu, . Mari kita membenarkan properti modul ini. Karena hasil bagi sama dengan produk, maka . Berdasarkan sifat sebelumnya, kita memiliki 
. Tetap hanya menggunakan persamaan , yang valid karena definisi modulus angka.
Properti modul berikut ditulis sebagai pertidaksamaan: 
, a , b dan c adalah bilangan real sembarang. Ketidaksetaraan tertulis tidak lebih dari pertidaksamaan segitiga. Untuk memperjelas hal ini, mari kita ambil titik A(a) , B(b) , C(c) pada garis koordinat, dan perhatikan segitiga ABC yang merosot, yang simpulnya terletak pada garis yang sama. Menurut definisi, modulus selisihnya sama dengan panjang segmen AB, - panjang segmen AC, dan - panjang segmen CB. Karena panjang salah satu sisi segitiga tidak melebihi jumlah panjang kedua sisi lainnya, maka pertidaksamaan 
, oleh karena itu, ketidaksetaraan juga berlaku.
Ketidaksetaraan yang baru saja dibuktikan jauh lebih umum dalam bentuk 
. Pertidaksamaan tertulis biasanya dianggap sebagai properti modul yang terpisah dengan rumusan: “ Modulus jumlah dua bilangan tidak melebihi jumlah modulus bilangan tersebut". Tapi pertidaksamaan langsung mengikuti dari pertidaksamaan , jika kita menempatkan b bukannya b di dalamnya, dan mengambil c=0 .
Modulus bilangan kompleks
Ayo berikan penentuan modulus bilangan kompleks. Mari kita diberi bilangan kompleks, ditulis dalam bentuk aljabar , di mana x dan y adalah beberapa bilangan real, masing-masing mewakili bagian real dan imajiner dari bilangan kompleks z yang diberikan, dan merupakan unit imajiner.
Definisi.
Modulus bilangan kompleks z=x+i y disebut akar kuadrat aritmatika dari jumlah kuadrat bagian nyata dan imajiner dari bilangan kompleks yang diberikan.
Modulus bilangan kompleks z dilambangkan sebagai , maka definisi modulus bilangan kompleks yang terdengar dapat ditulis sebagai 
.
Definisi ini memungkinkan Anda menghitung modulus bilangan kompleks apa pun dalam notasi aljabar. Sebagai contoh, mari kita hitung modulus bilangan kompleks. Dalam contoh ini, bagian real dari bilangan kompleks adalah , dan bagian imajinernya dikurangi empat. Kemudian, dengan definisi modulus bilangan kompleks, kita peroleh 
.
Interpretasi geometrik modulus bilangan kompleks dapat diberikan dalam bentuk jarak, dengan analogi interpretasi geometrik modulus bilangan real.
Definisi.
Modulus bilangan kompleks z adalah jarak dari awal bidang kompleks ke titik yang sesuai dengan angka z di bidang ini.
Menurut teorema Pythagoras, jarak dari titik O ke titik dengan koordinat (x, y) ditemukan sebagai , Oleh karena itu, , Dimana . Oleh karena itu, definisi terakhir dari modulus bilangan kompleks sesuai dengan yang pertama.
Definisi ini juga memungkinkan Anda untuk segera menunjukkan apa modulus bilangan kompleks z, jika ditulis dalam bentuk trigonometri sebagai 
atau dalam bentuk eksponensial. Di Sini . Misalnya, modulus bilangan kompleks 
adalah 5 , dan modulus bilangan kompleks adalah .
Dapat juga dilihat bahwa hasil kali bilangan kompleks dan konjugat kompleksnya menghasilkan jumlah kuadrat dari bagian real dan imajiner. Betulkah, . Persamaan yang dihasilkan memungkinkan kita untuk memberikan satu definisi lagi tentang modulus bilangan kompleks.
Definisi.
Modulus bilangan kompleks z adalah akar kuadrat aritmatika dari hasil kali bilangan ini dan konjugat kompleksnya, yaitu .
Sebagai kesimpulan, kami mencatat bahwa semua properti modul yang dirumuskan dalam subbagian yang sesuai juga berlaku untuk bilangan kompleks.
Bibliografi.
- Vilenkin N.Ya. dll. Matematika. Kelas 6: buku teks untuk lembaga pendidikan.
- Makarychev Yu.N., Mindyuk N.G., Neshkov K.I., Suvorova S.B. Aljabar: buku teks untuk 8 sel. institusi pendidikan.
- Lunts G.L., Elsgolts L.E. Fungsi variabel kompleks: buku teks untuk universitas.
- Privalov I.I. Pengantar teori fungsi variabel kompleks.
Kita telah mengetahui bahwa himpunan bilangan real $R$ dibentuk oleh bilangan rasional dan irasional.
Bilangan rasional selalu dapat direpresentasikan sebagai desimal (periodik terbatas atau tak terbatas).
Bilangan irasional ditulis sebagai desimal tak terbatas tetapi tidak berulang.
Himpunan bilangan real $R$ juga mencakup elemen $-\infty $ dan $+\infty $, yang pertidaksamaannya $-\infty
Pertimbangkan cara untuk mewakili bilangan real.
pecahan biasa
Pecahan biasa ditulis menggunakan dua bilangan asli dan batang pecahan horizontal. Bilah pecahan sebenarnya menggantikan tanda pembagian. Bilangan di bawah garis adalah penyebut (pembagi), bilangan di atas garis adalah pembilangnya (dibagi).
Definisi
Suatu pecahan disebut wajar jika pembilangnya lebih kecil dari penyebutnya. Sebaliknya, suatu pecahan disebut tidak wajar jika pembilangnya lebih besar atau sama dengan penyebutnya.
Untuk pecahan biasa, ada aturan perbandingan sederhana, praktis jelas ($m$,$n$,$p$ adalah bilangan asli):
- dari dua pecahan dengan penyebut yang sama, pecahan dengan pembilang yang lebih besar lebih besar, yaitu $\frac(m)(p) >\frac(n)(p) $ for $m>n$;
- dari dua pecahan dengan pembilang yang sama, pecahan dengan penyebut yang lebih kecil lebih besar, yaitu $\frac(p)(m) >\frac(p)(n) $ untuk $ m
- pecahan biasa selalu kurang dari satu; pecahan tak wajar selalu lebih besar dari satu; pecahan yang pembilangnya sama dengan penyebutnya sama dengan satu;
- Setiap pecahan tidak wajar lebih besar dari pecahan biasa mana pun.
Bilangan desimal
Notasi bilangan desimal (pecahan desimal) memiliki bentuk: bagian bilangan bulat, titik desimal, bagian pecahan. Notasi desimal dari pecahan biasa dapat diperoleh dengan membagi "sudut" pembilang dengan penyebut. Ini dapat menghasilkan pecahan desimal terbatas atau pecahan desimal periodik tak terbatas.
Definisi
Angka pecahan disebut tempat desimal. Dalam hal ini, digit pertama setelah koma disebut digit persepuluh, digit kedua - seperseratus, digit ketiga - seperseribu, dll.
Contoh 1
Kami menentukan nilai angka desimal 3,74. Kami mendapatkan: $3,74=3+\frac(7)(10) +\frac(4)(100) $.
Bilangan desimal dapat dibulatkan. Dalam hal ini, Anda harus menentukan digit yang akan dilakukan pembulatan.
Aturan pembulatannya adalah sebagai berikut:
- semua angka di sebelah kanan angka ini diganti dengan nol (jika angka-angka ini sebelum titik desimal) atau dibuang (jika angka-angka ini berada setelah titik desimal);
- jika digit pertama setelah digit yang diberikan kurang dari 5, maka digit digit ini tidak diubah;
- jika angka pertama setelah angka yang diberikan adalah 5 atau lebih, maka angka dari angka ini ditambah satu.
Contoh 2
- Mari kita bulatkan angka 17302 ke ribuan terdekat: 17000.
- Mari kita bulatkan angka 17378 ke ratusan terdekat: 17400.
- Mari kita bulatkan angka 17378,45 menjadi puluhan: 17380.
- Mari kita bulatkan angka 378.91434 ke perseratus terdekat: 378.91.
- Mari kita bulatkan angka 378.91534 ke perseratus terdekat: 378.92.
Mengubah bilangan desimal menjadi pecahan biasa.
Kasus 1
Bilangan desimal adalah desimal berakhir.
Metode konversi ditunjukkan dalam contoh berikut.
Contoh 2
Kami memiliki: $3,74=3+\frac(7)(10) +\frac(4)(100) $.
Kurangi menjadi penyebut yang sama dan dapatkan:
Pecahan dapat dikurangi: $3,74=\frac(374)(100) =\frac(187)(50) $.
Kasus 2
Bilangan desimal adalah desimal berulang yang tak terbatas.
Metode transformasi didasarkan pada kenyataan bahwa bagian periodik dari pecahan desimal periodik dapat dianggap sebagai jumlah anggota deret geometri menurun tak terbatas.
Contoh 4
$0,\kiri(74\kanan)=\frac(74)(100) +\frac(74)(10000) +\frac(74)(1000000) +\ldots $. Anggota pertama dari progres adalah $a=0.74$, penyebut dari progresi adalah $q=0.01$.
Contoh 5
$0,5\kiri(8\kanan)=\frac(5)(10) +\frac(8)(100) +\frac(8)(1000) +\frac(8)(10000) +\ldots $ . Anggota pertama dari kemajuan adalah $a=0,08$, penyebut dari kemajuan adalah $q=0,1$.
Jumlah suku-suku barisan geometri menurun tak hingga dihitung dengan rumus $s=\frac(a)(1-q) $, dengan $a$ suku pertama dan $q$ penyebut barisan $ \kiri (0
Contoh 6
Mari kita ubah pecahan desimal periodik tak hingga $0,\left(72\right)$ menjadi pecahan biasa.
Anggota pertama dari progres adalah $a=0.72$, penyebut dari progresi adalah $q=0.01$. Kita peroleh: $s=\frac(a)(1-q) =\frac(0.72)(1-0.01) =\frac(0.72)(0.99) =\frac(72)( 99) =\frac(8 )(11)$. Jadi $0,\kiri(72\kanan)=\frac(8)(11) $.
Contoh 7
Mari kita ubah pecahan desimal periodik tak hingga $0,5\kiri(3\kanan)$ menjadi pecahan biasa.
Anggota pertama dari progres adalah $a=0.03$, penyebut dari progres adalah $q=0.1$. Kita peroleh: $s=\frac(a)(1-q) =\frac(0.03)(1-0.1) =\frac(0.03)(0.9) =\frac(3)( 90) =\frac(1 )(30)$.
Jadi $0,5\kiri(3\kanan)=\frac(5)(10) +\frac(1)(30) =\frac(5\cdot 3)(10\cdot 3) +\frac( 1)(30 ) =\frac(15)(30) +\frac(1)(30) =\frac(16)(30) =\frac(8)(15) $.
Bilangan real dapat diwakili oleh titik-titik pada garis bilangan.
Dalam hal ini, kami menyebut sumbu numerik sebagai garis tak hingga di mana titik asal (titik $O$), arah positif (ditunjukkan oleh panah) dan skala (untuk menampilkan nilai) dipilih.
Antara semua bilangan real dan semua titik sumbu numerik ada korespondensi satu-satu: setiap titik sesuai dengan satu angka dan, sebaliknya, setiap angka sesuai dengan satu titik. Oleh karena itu, himpunan bilangan real kontinu dan tak terbatas dengan cara yang sama seperti sumbu bilangan kontinu dan tak terbatas.
Beberapa himpunan bagian dari himpunan bilangan real disebut interval numerik. Unsur-unsur interval numerik adalah bilangan $x\dalam R$ yang memenuhi pertidaksamaan tertentu. Biarkan $a\di R$, $b\di R$ dan $a\le b$. Dalam hal ini, jenis kesenjangan dapat sebagai berikut:
- Interval $\kiri(a,\; b\kanan)$. Pada saat yang sama $a
- Segmen $\kiri$. Selain itu, $a\le x\le b$.
- Setengah-segmen atau setengah-interval $\left$. Pada saat yang sama $a \le x
- Rentang tak terbatas, misalnya $a
Sangat penting juga semacam interval, yang disebut lingkungan suatu titik. Lingkungan dari titik tertentu $x_(0) \in R$ adalah interval arbitrer $\left(a,\; b\right)$ yang berisi titik ini di dalam dirinya sendiri, yaitu $a 0$ - radius 10.
Nilai mutlak dari bilangan
Nilai mutlak (atau modulus) dari bilangan real $x$ adalah bilangan real non-negatif $\left|x\right|$, didefinisikan oleh rumus: $\left|x\right|=\left\(\ mulai(array)(c) (\; \; x\; \; (\rm aktif)\; \; x\ge 0) \\ (-x\; \; (\rm aktif)\; \; x
Secara geometris, $\left|x\right|$ berarti jarak antara titik $x$ dan 0 pada sumbu nyata.
Sifat nilai mutlak:
- berikut dari definisi bahwa $\left|x\right|\ge 0$, $\left|x\right|=\left|-x\right|$;
- untuk modulus penjumlahan dan modulus selisih dua bilangan, pertidaksamaan $\left|x+y\right|\le \left|x\right|+\left|y\right|$, $\ kiri|x-y\kanan|\le \kiri|x\kanan|+\kiri|y\kanan|$ dan juga $\kiri|x+y\kanan|\ge \kiri|x\kanan|-\kiri|y \kanan|$,$\ kiri|x-y\kanan|\ge \kiri|x\kanan|-\kiri|y\kanan|$;
- modulus hasil kali dan modulus hasil bagi dua bilangan memenuhi persamaan $\left|x\cdot y\right|=\left|x\right|\cdot \left|y\right|$ dan $\left |\frac(x)( y) \kanan|=\frac(\kiri|x\kanan|)(\kiri|y\kanan|) $.
Berdasarkan definisi nilai mutlak untuk bilangan arbitrer $a>0$, kita juga dapat menetapkan ekivalensi dari pasangan pertidaksamaan berikut:
- jika $ \kiri|x\kanan|
- jika $\left|x\right|\le a$ maka $-a\le x\le a$;
- jika $\left|x\right|>a$ maka $xa$;
- jika $\left|x\right|\ge a$, maka $x\le -a$ atau $x\ge a$.
Contoh 8
Selesaikan pertidaksamaan $\left|2\cdot x+1\right|
Pertidaksamaan ini setara dengan pertidaksamaan $-7
Dari sini kita mendapatkan: $-8
