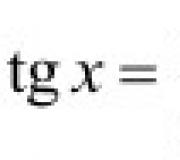Kriteri për varësinë lineare të vektorëve në rn. Tre lloje të varësisë lineare

Kusht paraprak varësia lineare e n funksioneve.

Le të kenë funksionet derivate të kufirit (n-1).

Merrni parasysh përcaktorin: (1)

W(x) zakonisht quhet përcaktor Wronski për funksionet.

Teorema 1. Nëse funksionet varen linearisht në intervalin (a,b), atëherë Wronskian W(x) i tyre është identikisht i barabartë me zero në këtë interval.

Dëshmi. Sipas kushteve të teoremës, relacioni është i kënaqur

, (2) ku jo të gjitha janë të barabarta me zero. Le . Pastaj

(3). Ne e dallojmë këtë identitet n-1 herë dhe,

duke zëvendësuar vlerat e tyre rezultuese në përcaktuesin Wronsky,

marrim:

Në përcaktorin e Wronskit, kolona e fundit është një kombinim linear i kolonave të mëparshme n-1 dhe për këtë arsye është e barabartë me zero në të gjitha pikat e intervalit (a,b).

Teorema 2. Nëse funksionet y 1 ,..., y n janë zgjidhje lineare të pavarura të ekuacionit L[y] = 0, të gjithë koeficientët e të cilit janë të vazhdueshëm në intervalin (a,b), atëherë Wronskiani i këtyre zgjidhjeve është jozero në secilën prej tyre. intervali i pikës (a,b).

Dëshmi. Le të supozojmë të kundërtën. Ka X 0, ku W(X 0)=0. Le të krijojmë një sistem n ekuacionesh

Natyrisht, sistemi (5) ka një zgjidhje jo zero. Le të (6).

Le të bëjmë një kombinim linear të zgjidhjeve y 1,..., y n.

Y(x) është zgjidhje e ekuacionit L[y] = 0. Përveç kësaj, . Në bazë të teoremës së unike, zgjidhja e ekuacionit L[y] = 0 me kushte fillestare zero duhet të jetë vetëm zero, ᴛ.ᴇ. .

Ne marrim identitetin ku jo të gjitha janë të barabarta me zero, që do të thotë se y 1 ,..., y n janë të varura linearisht, gjë që bie ndesh me kushtet e teoremës. Rrjedhimisht, nuk ka asnjë pikë të tillë ku W(X 0)=0.

Bazuar në Teoremën 1 dhe Teoremën 2, mund të formulohet pohimi i mëposhtëm. Në mënyrë që n zgjidhje të ekuacionit L[y] = 0 të jenë linearisht të pavarura në intervalin (a,b), është jashtëzakonisht e rëndësishme dhe e mjaftueshme që Wronskian-i i tyre të mos zhduket në asnjë pikë të këtij intervali.

Vetitë e mëposhtme të dukshme të Wronskian-it rrjedhin gjithashtu nga teoremat e provuara.

1. Nëse Wronskiani i n zgjidhjeve të ekuacionit L[y] = 0 është i barabartë me zero në një pikë x = x 0 nga intervali (a,b), në të cilin të gjithë koeficientët p i (x) janë të vazhdueshëm, atëherë ai është i barabartë në zero në çdo kohë ex pikat e këtij intervali.
2. Nëse Wronskiani i n zgjidhjeve të ekuacionit L[y] = 0 është jozero në një pikë x = x0 nga intervali (a,b), atëherë është jozero në të gjitha pikat e këtij intervali.

Megjithatë, për linearitetin e n zgjidhjeve të pavarura të ekuacionit L[y] = 0 në intervalin (a,b), në të cilin koeficientët e ekuacionit p i (x) janë të vazhdueshëm, është jashtëzakonisht e rëndësishme dhe e mjaftueshme që Wronskian-i i tyre. të jetë i ndryshëm nga zero të paktën një pikë e këtij intervali.

Një kusht i domosdoshëm për varësinë lineare të n funksioneve. - koncepti dhe llojet. Klasifikimi dhe veçoritë e kategorisë “Kushti i domosdoshëm për varësinë lineare të n funksioneve”. 2017, 2018.

Pajisjet për trajtimin e ngarkesave në bord Ligjërata nr. 6 Tema: Pajisjet e ngarkesave 6.1. Pajisje për trajtimin e ngarkesave në bord. 6.2. Vinça mallrash. 6.3. Rampë. Mbingarkesa është lëvizja e ngarkesës mbi ose nga automjeti. Shumë... .

Përkufizimi 18.2 Sistemi i funksionitf, ..., f fqthirrurli- neip o h dhe në dhe me dhe m rreth th në interval(A, (3), nëse disa joparëndësishme 5 një kombinim linear i këtyre funksioneve është i barabartë me zero në këtë interval në mënyrë identike:

Përkufizimi 18.3 Sistemi vektorial f 1, ..., x n thuhet se është linear në një b i c i m nëse një kombinim jo i parëndësishëm, linear i këtyre vektorëve është i barabartë me vektorin e pikës:

L Për të shmangur konfuzionin, në atë që vijon do të shënojmë numrin e komponentit vektor (funksioni vektor) me nënshkrimin dhe numrin e vetë vektorit (nëse ka disa vektorë të tillë) me indeksin e sipërm.

“Ju kujtojmë se një kombinim linear quhet jo i parëndësishëm nëse jo të gjithë koeficientët në të janë zero.

Përkufizimi 18.4 Sistemi i funksioneve vektoriale x 1 ^),..., x n (t) quhet linear h dhe brenda dhe me dhe në interval,(A, /3), nëse një kombinim linear jo i parëndësishëm i këtyre funksioneve vektoriale është identikisht i barabartë me vektorin zero në këtë interval:

Është e rëndësishme të kuptohet lidhja midis këtyre tre koncepteve (varësia lineare e funksioneve, vektorëve dhe funksioneve vektoriale) me njëri-tjetrin.

Para së gjithash, nëse e paraqesim formulën (18.6) në formë të zgjeruar (duke kujtuar se secili prej x g (1)është një vektor)

atëherë rezulton ekuivalent me sistemin e barazive

që do të thotë lineare varësia nga g-x komponentë në kuptimin e përkufizimit të parë (si funksione). Ata thonë se varësia lineare e funksioneve vektoriale i përfshin ato komponent pas komponenti varësia lineare.

E kundërta, në përgjithësi, nuk është e vërtetë: mjafton të shqyrtojmë shembullin e një çifti funksionesh vektoriale.

Komponentët e parë të këtyre funksioneve vektoriale thjesht përputhen, që do të thotë se ata janë të varur në mënyrë lineare. Komponentët e dytë janë proporcionalë, d.m.th. janë gjithashtu të varura në mënyrë lineare. Megjithatë, nëse përpiqemi të ndërtojmë kombinimin e tyre linear, i cili është identikisht i barabartë me zero, atëherë nga relacioni

ne e marrim sistemin menjëherë

e cila ka një zgjidhje unike S - S-2 - 0. Kështu, funksionet tona vektoriale janë linearisht të pavarura.

Cila është arsyeja e kësaj pasurie të çuditshme? Cili është truku që ju lejon të ndërtoni funksione vektoriale të pavarura lineare nga funksione dukshëm të varura?

Rezulton se e gjithë pika nuk është aq shumë në varësinë lineare të përbërësve, por në proporcionin e koeficientëve që është i nevojshëm për të marrë zero. Në rastin e varësisë lineare të funksioneve vektoriale, i njëjti grup koeficientësh u shërben të gjithë komponentëve pavarësisht nga numri. Por në shembullin që dhamë, një komponent kërkonte një përqindje koeficientësh dhe një tjetër kërkonte një tjetër. Pra, truku është në të vërtetë i thjeshtë: për të përftuar një varësi lineare të funksioneve vektoriale në tërësi nga një varësi lineare "përsa i përket komponentëve", është e nevojshme që të gjithë përbërësit të varen në mënyrë lineare "në të njëjtin proporcion".

Le të kalojmë tani në studimin e lidhjes midis varësisë lineare të funksioneve vektoriale dhe vektorëve. Këtu është pothuajse e qartë se nga varësia lineare e funksioneve vektoriale rrjedh se për çdo fikse t* vektoriale

do të jetë i varur në mënyrë lineare.

E kundërta, në përgjithësi, nuk qëndron: nga varësia lineare e vektorëve për secilin t Varësia lineare e funksioneve vektoriale nuk pason. Kjo është e lehtë për t'u parë duke përdorur shembullin e dy funksioneve vektoriale

Në t=1, t=2 dhe t=3 marrim çifte vektorësh

përkatësisht. Çdo çift vektorësh është proporcional (me koeficientët përkatësisht 1,2 dhe 3). Është e lehtë të kuptohet se për çdo fikse t*çifti ynë i vektorëve do të jetë proporcional me koeficientin t*.

Nëse përpiqemi të ndërtojmë një kombinim linear të funksioneve vektoriale që është identikisht i barabartë me zero, atëherë tashmë përbërësit e parë na japin relacionin

e cila është e mundur vetëm nëse ME = ME2 = 0. Kështu, funksionet tona vektoriale rezultuan të jenë linearisht të pavarur. Përsëri, shpjegimi për këtë efekt është se në rastin e varësisë lineare të funksioneve vektoriale, i njëjti grup konstantesh Cj u shërben të gjitha vlerave t, dhe në shembullin tonë për secilën vlerë t kërkohej një proporcion specifik ndërmjet koeficientëve.

Prezantuar nga ne veprime lineare në vektorë bëjnë të mundur krijimin e shprehjeve të ndryshme për sasive vektoriale dhe transformojini ato duke përdorur vetitë e vendosura për këto operacione.

Bazuar në një grup të caktuar vektorësh a 1, ..., a n, mund të krijoni një shprehje të formës

ku a 1, ..., dhe n janë arbitrare numra realë. Kjo shprehje quhet kombinim linear i vektorëve a 1, ..., a n. Numrat α i, i = 1, n, përfaqësojnë koeficientët e kombinimit linear. Një grup vektorësh quhet gjithashtu sistemi i vektorëve.

Në lidhje me konceptin e paraqitur të një kombinimi linear vektorësh, lind problemi i përshkrimit të një grupi vektorësh që mund të shkruhet si një kombinim linear i një sistemi të caktuar vektorësh a 1, ..., a n. Për më tepër, ekzistojnë pyetje të natyrshme në lidhje me kushtet në të cilat ekziston një paraqitje e një vektori në formën e një kombinimi linear dhe për veçantinë e një paraqitjeje të tillë.

Përkufizimi 2.1. Quhen vektorët a 1, ..., dhe n varur në mënyrë lineare, nëse ekziston një grup koeficientësh α 1 , ... , α n të tillë që

α 1 a 1 + ... + α n а n = 0 (2.2)

dhe të paktën njëri prej këtyre koeficientëve është jo zero. Nëse grupi i specifikuar i koeficientëve nuk ekziston, atëherë thirren vektorët i pavarur në mënyrë lineare.

Nëse α 1 = ... = α n = 0, atëherë, padyshim, α 1 a 1 + ... + α n a n = 0. Duke pasur parasysh këtë, mund të themi këtë: vektorët a 1, ..., dhe n janë linearisht të pavarur nëse nga barazia (2.2) rezulton se të gjithë koeficientët α 1 , ... , α n janë të barabartë me zero.

Teorema e mëposhtme shpjegon pse koncepti i ri quhet termi "varësi" (ose "pavarësi") dhe ofron një kriter të thjeshtë për varësinë lineare.

Teorema 2.1. Në mënyrë që vektorët a 1, ..., dhe n, n > 1, të jenë të varur linearisht, është e nevojshme dhe e mjaftueshme që njëri prej tyre të jetë një kombinim linear i të tjerëve.

◄ Domosdoshmëri. Le të supozojmë se vektorët a 1, ..., dhe n janë të varur në mënyrë lineare. Sipas përkufizimit 2.1 të varësisë lineare, në barazinë (2.2) në të majtë ka të paktën një koeficient jozero, për shembull α 1. Duke e lënë termin e parë në anën e majtë të barazisë, ne zhvendosim pjesën tjetër në anën e djathtë, duke ndryshuar shenjat e tyre, si zakonisht. Duke pjesëtuar barazinë që rezulton me α 1, marrim

a 1 =-α 2 /α 1 ⋅ a 2 - ... - α n /α 1 ⋅ a n

ato. paraqitja e vektorit a 1 si një kombinim linear i vektorëve të mbetur a 2, ..., a n.

Përshtatshmëria. Le të, për shembull, vektori i parë a 1 mund të përfaqësohet si një kombinim linear i vektorëve të mbetur: a 1 = β 2 a 2 + ... + β n a n. Duke transferuar të gjithë termat nga ana e djathtë në të majtë, marrim një 1 - β 2 a 2 - ... - β n a n = 0, d.m.th. një kombinim linear i vektorëve a 1, ..., a n me koeficientë α 1 = 1, α 2 = - β 2, ..., α n = - β n, e barabartë me vektor zero. Në këtë kombinim linear, jo të gjithë koeficientët janë zero. Sipas përkufizimit 2.1, vektorët a 1, ..., dhe n janë të varur në mënyrë lineare.

Përkufizimi dhe kriteri për varësinë lineare janë formuluar për të nënkuptuar praninë e dy ose më shumë vektorëve. Sidoqoftë, mund të flasim gjithashtu për një varësi lineare të një vektori. Për të realizuar këtë mundësi, në vend të "vektorët janë të varur në mënyrë lineare", duhet të thoni "sistemi i vektorëve është i varur në mënyrë lineare". Është e lehtë të shihet se shprehja "një sistem i një vektori është i varur në mënyrë lineare" do të thotë se ky vektor i vetëm është zero (në një kombinim linear ka vetëm një koeficient, dhe ai nuk duhet të jetë i barabartë me zero).

Koncepti i varësisë lineare ka një interpretim të thjeshtë gjeometrik. Tre deklaratat e mëposhtme sqarojnë këtë interpretim.

Teorema 2.2. Dy vektorë janë të varur linearisht nëse dhe vetëm nëse ata kolineare.

◄ Nëse vektorët a dhe b janë të varur në mënyrë lineare, atëherë njëri prej tyre, për shembull a, shprehet përmes tjetrit, d.m.th. a = λb për një numër real λ. Sipas përkufizimit 1.7 punon vektorët për numër, vektorët a dhe b janë kolinear.

Le të jenë tani vektorët a dhe b kolinear. Nëse të dyja janë zero, atëherë është e qartë se ato janë të varura në mënyrë lineare, pasi çdo kombinim linear i tyre është i barabartë me vektorin zero. Le të mos jetë një nga këta vektorë të barabartë me 0, për shembull vektori b. Le të shënojmë me λ raportin e gjatësive të vektorit: λ = |a|/|b|. Vektorët kolinearë mund të jenë njëdrejtimëshe ose drejtuar në të kundërt. Në rastin e fundit, ne ndryshojmë shenjën e λ. Pastaj, duke kontrolluar përkufizimin 1.7, jemi të bindur se a = λb. Sipas teoremës 2.1, vektorët a dhe b janë të varur në mënyrë lineare.

Vërejtje 2.1. Në rastin e dy vektorëve, duke marrë parasysh kriterin e varësisë lineare, teorema e provuar mund të riformulohet si më poshtë: dy vektorë janë kolinear nëse dhe vetëm nëse njëri prej tyre përfaqësohet si prodhim i tjetrit me një numër. Ky është një kriter i përshtatshëm për kolinearitetin e dy vektorëve.

Teorema 2.3. Tre vektorë janë të varur linearisht nëse dhe vetëm nëse ata koplanare.

◄ Nëse tre vektorë a, b, c janë të varur linearisht, atëherë, sipas teoremës 2.1, njëri prej tyre, për shembull a, është një kombinim linear i të tjerëve: a = βb + γс. Le të kombinojmë origjinën e vektorëve b dhe c në pikën A. Atëherë vektorët βb, γс do të kenë një origjinë të përbashkët në pikën A dhe përgjatë sipas rregullit të paralelogramit, shuma e tyre është ato. vektori a do të jetë një vektor me origjinë A dhe fund, e cila është kulmi i një paralelogrami të ndërtuar mbi vektorët përbërës. Kështu, të gjithë vektorët shtrihen në të njëjtin rrafsh, d.m.th., koplanar.

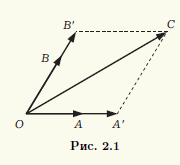
Le të jenë koplanarë vektorët a, b, c. Nëse njëri prej këtyre vektorëve është zero, atëherë është e qartë se do të jetë një kombinim linear i të tjerëve. Mjafton të merren të gjithë koeficientët e kombinimit linear e barabartë me zero. Prandaj, mund të supozojmë se të tre vektorët nuk janë zero. E përputhshme filloi këta vektorë në pikë e përbashkët O. Fundet e tyre le të jenë përkatësisht pikat A, B, C (Fig. 2.1). Nëpër pikën C vizatojmë drejtëza paralele me drejtëza që kalojnë nëpër çifte pikash O, A dhe O, B. Duke përcaktuar pikat e kryqëzimit si A" dhe B", marrim një paralelogram OA"CB", pra, OC" = OA" + OB". Vektori OA" dhe vektori jozero a = OA janë kolinear, dhe për këtë arsye i pari prej tyre mund të merret duke shumëzuar të dytin me një numër real α:OA" = αOA. Në mënyrë të ngjashme, OB" = βOB, β ∈ R. Si rezultat, marrim se OC" = α OA. + βOB, pra vektori c është një kombinim linear i vektorëve a dhe b. Sipas teoremës 2.1, vektorët a, b, c janë të varur linearisht.

Teorema 2.4.Çdo katër vektorë janë të varur në mënyrë lineare.

◄ Ne e kryejmë vërtetimin sipas të njëjtës skemë si në teoremën 2.3. Konsideroni katër vektorë arbitrarë a, b, c dhe d. Nëse njëri nga katër vektorët është zero, ose midis tyre ka dy vektorë kolinearë, ose tre nga katër vektorët janë koplanarë, atëherë këta katër vektorë janë të varur në mënyrë lineare. Për shembull, nëse vektorët a dhe b janë kolinearë, atëherë mund të bëjmë kombinimin e tyre linear αa + βb = 0 me koeficientë jo zero, dhe më pas të shtojmë dy vektorët e mbetur në këtë kombinim, duke marrë zero si koeficientë. Ne marrim një kombinim linear të katër vektorëve të barabartë me 0, në të cilët ka koeficientë jo zero.

Kështu, mund të supozojmë se midis katër vektorëve të zgjedhur, asnjë vektor nuk është zero, asnjë dy nuk është kolinear dhe asnjë tre nuk është koplanar. Le të zgjedhim pikën O si fillimin e tyre të përbashkët Pastaj skajet e vektorëve a, b, c, d do të jenë disa pika A, B, C, D (Fig. 2.2). Nëpër pikën D vizatojmë tre rrafshe paralel me rrafshet OBC, OCA, OAB dhe le të jenë A", B", C" pikat e prerjes së këtyre rrafsheve përkatësisht me drejtëzat OA, OB, OS. Përftojmë një paralelipiped OA" C "B" C" B"DA", dhe vektorët a, b, c shtrihen në skajet e tij që dalin nga kulmi O. Meqenëse katërkëndëshi OC"DC" është një paralelogram, atëherë OD = OC" + OC "Nga ana tjetër, segmenti OC" është një paralelogram OA"C"B", pra OC" = OA" + OB" dhe OD = OA" + OB" + OC".

Mbetet të theksohet se çiftet e vektorëve OA ≠ 0 dhe OA" , OB ≠ 0 dhe OB" , OC ≠ 0 dhe OC" janë kolinearë dhe, për rrjedhojë, është e mundur të zgjidhen koeficientët α, β, γ në mënyrë që OA" = αOA , OB" = βOB dhe OC" = γOC. Më në fund marrim OD = αOA + βOB + γOC. Rrjedhimisht, vektori OD shprehet përmes tre vektorëve të tjerë, dhe të katër vektorët, sipas Teoremës 2.1, janë të varur në mënyrë lineare.

Një kusht i domosdoshëm dhe i mjaftueshëm për varësinë lineare të dy

vektorët është kolineariteti i tyre.

2. Produkt skalar- një veprim në dy vektorë, rezultati i të cilit është një skalar (numër) që nuk varet nga sistemi i koordinatave dhe karakterizon gjatësinë e vektorëve të faktorëve dhe këndin ndërmjet tyre. Ky operacion korrespondon me shumëzimin gjatësia dhënë vektor x on projeksioni një vektor tjetër y në një vektor të dhënë x. Ky operacion zakonisht konsiderohet të jetë komutativ dhe linear në secilin faktor.

Karakteristikat e produktit me pika:

3. Tre vektorë (ose numër më i madh) quhen koplanare, nëse ata, duke u reduktuar në një origjinë të përbashkët, shtrihen në të njëjtin rrafsh.

Një kusht i domosdoshëm dhe i mjaftueshëm për varësinë lineare të tre vektorëve është bashkëplanariteti i tyre. Baza në hapësirë është çdo treshe e renditur e vektorëve jokoplanarë. Një bazë në hapësirë ​​lejon që çdo vektor të lidhet në mënyrë unike me një treshe të renditur numrash - koeficientët e paraqitjes së këtij vektori në një kombinim linear të vektorëve bazë. Përkundrazi, ne shoqërojmë një vektor me çdo treshe të renditur numrash duke përdorur një bazë nëse bëjmë një kombinim linear ortonormale , nëse vektorët e tij janë të barabartë në gjatësi me një. Për një bazë ortonormale në hapësirë, shpesh përdoret shënimi. Teorema: Në bazë ortonormale, koordinatat e vektorëve janë projeksionet ortogonale përkatëse të këtij vektori në drejtimet e vektorëve të koordinatave. Trefishi i vektorëve jokoplanarë a, b, c thirrur drejtë, nëse vëzhguesi nga origjina e tyre e përbashkët anashkalon skajet e vektorëve a, b, c në rendin e dhënë duket se ndodh në drejtim të akrepave të orës. Përndryshe a, b, c - la tre. Quhen të gjitha trefishat djathtas (ose majtas) të vektorëve të orientuar në mënyrë të barabartë. Një sistem koordinativ drejtkëndor në një rrafsh formohet nga dy boshte koordinative reciproke pingule OK Dhe OY. Boshtet e koordinatave kryqëzohen në pikë O, që quhet origjina, në çdo bosht zgjidhet drejtimi pozitiv. NË me anën e djathtë sistemi i koordinatave, drejtimi pozitiv i boshteve zgjidhet në mënyrë që kur boshti të drejtohet OY lart, bosht OK shikonte djathtas.

Katër qoshe (I, II, III, IV) të formuara nga boshtet koordinative X"X Dhe Y"Y, quhen kënde koordinative ose kuadrantet(shih Fig. 1).

nëse vektorët dhe në lidhje me një bazë ortonormale në plan kanë koordinata dhe, përkatësisht, atëherë produkti skalar i këtyre vektorëve llogaritet me formulën

4. Prodhimi kryq i dy vektorëve a dhe bështë një operacion mbi to, i përcaktuar vetëm në hapësirë ​​tredimensionale, rezultati i të cilit është vektoriale me sa vijon

Vetitë:

Kuptimi gjeometrik i produktit vektorial të vektorëve është zona e një paralelogrami të ndërtuar mbi vektorë. Një kusht i domosdoshëm dhe i mjaftueshëm për kolinearitetin e një vektori jozero dhe një vektori është ekzistenca e një numri që plotëson barazinë.

Nëse dy vektorë dhe përcaktohen nga drejtkëndëshi i tyre Koordinatat karteziane, ose më saktë, janë të përfaqësuar në një bazë vortonormed

dhe sistemi i koordinatave është i drejtë, atëherë i tyre produkt vektorial duket si

Për të kujtuar këtë formulë, është e përshtatshme të përdorni përcaktuesin:

5. Produkt i përzier vektorë - prodhimi skalar i një vektori dhe prodhimi vektorial i vektorëve dhe :

Ndonjëherë quhet produkt skalar i trefishtë vektorë, ka shumë të ngjarë për faktin se rezultati është një skalar (më saktë, një pseudoscalar).

Kuptimi gjeometrik: Moduli i produktit të përzier numerikisht është i barabartë me vëllimin e paralelepipedit të formuar nga vektorët.

Kur dy faktorë riorganizohen, produkti i përzier ndryshon shenjën në të kundërtën:

Me një rirregullim ciklik (rrethor) të faktorëve, produkti i përzier nuk ndryshon:

Produkti i përzier është linear në çdo faktor.

Produkti i përzier është zero nëse dhe vetëm nëse vektorët janë koplanarë.

1. Kushti për bashkëplanaritetin e vektorëve: Tre vektorë janë koplanarë nëse dhe vetëm nëse produkti i tyre i përzier është zero.

§ Një treshe vektorësh që përmbajnë një çift vektorësh kolinearë është koplanar.

§ Prodhim i përzier i vektorëve koplanarë. Ky është një kriter për bashkëplanaritetin e tre vektorëve.

§ Vektorët koplanarë janë të varur në mënyrë lineare. Ky është gjithashtu një kriter për koplanaritetin.

§ Ka numra realë të tillë që për koplanar , me përjashtim të rasteve të ose . Ky është një riformulim i pronës së mëparshme dhe gjithashtu një kriter i bashkëplanaritetit.

§ Në hapësirën 3-dimensionale, 3 vektorë joplanarë përbëjnë bazën. Domethënë, çdo vektor mund të paraqitet në formën: . Pastaj ato do të jenë koordinata në këtë bazë.

Produkti i përzier në sistemin e duhur të koordinatave karteziane (në bazë ortonormale) është i barabartë me përcaktuesin e matricës së përbërë nga vektorë dhe:

§ 6. Ekuacioni i përgjithshëm (i plotë) i rrafshit

ku dhe janë konstante, dhe në të njëjtën kohë ato nuk janë të barabarta me zero; në formë vektoriale:

ku është vektori i rrezes së pikës, vektori është pingul me rrafshin (vektor normal). Kosinuset e drejtimit vektor:

Nëse një nga koeficientët në një ekuacion të rrafshët është zero, quhet ekuacioni jo të plota. Kur rrafshi kalon nga origjina e koordinatave, kur (ose , ) rrafshi është paralel me boshtin (përkatësisht ose ). Kur ( , ose ) rrafshi është paralel me rrafshin (përkatësisht ose ).

§ Ekuacioni i një rrafshi në segmente:

ku , , janë segmentet e prera nga rrafshi në boshtet dhe.

§ Ekuacioni i një rrafshi që kalon nëpër një pikë pingul me vektorin normal :

në formë vektoriale:

(produkt i përzier i vektorëve), përndryshe

§ Ekuacioni i rrafshit normal (i normalizuar).

§ Këndi ndërmjet dy rrafsheve. Nëse ekuacionet e P. janë dhënë në formën (1), atëherë

Nëse në formë vektoriale, atëherë

§ Planet janë paralele, Nëse

Ose (produkt vektor)

§ Planet janë pingul, Nëse

Ose . (Produkt skalar)

7. Ekuacioni i një rrafshi që kalon nëpër tre pika të dhëna , duke mos u shtrirë në të njëjtën vijë të drejtë:

8. Distanca nga një pikë në një rrafsh është më e vogla nga distancat ndërmjet kësaj pike dhe pikave të rrafshit. Dihet se distanca nga një pikë në një plan është e barabartë me gjatësinë e pingulit të tërhequr nga kjo pikë në rrafsh.

§ Devijimi i pikës nga rrafshi i dhënë nga ekuacioni i normalizuar

Nëse dhe origjina e koordinatave qëndrojnë së bashku anët e ndryshme aeroplan, përndryshe. Distanca nga një pikë në një aeroplan është

§ Distanca nga pika në planin e specifikuar nga ekuacioni llogaritet me formulën:

9. Një tufë avionësh- ekuacioni i çdo komploti që kalon në vijën e kryqëzimit të dy rrafsheve

ku α dhe β janë çdo numër që nuk është zero njëkohësisht.

Në mënyrë që të tre rrafshet e përcaktuara nga tyre ekuacionet e përgjithshme A 1 x+B 1 y+C 1 z+D 1 =0, A 2 x+B 2 y+C 2 z+D 2 =0, A 3 x+B 3 y+C 3 z+D 3 =0 në lidhje me PDSC-të që i përkisnin një grupi, të duhur ose të papërshtatshëm, është e nevojshme dhe e mjaftueshme që rangu i matricës të jetë i barabartë me dy ose një.
Teorema 2. Le të jepen dy plane π 1 dhe π 2 në lidhje me PDSC nga ekuacionet e tyre të përgjithshme: A 1 x+B 1 y+C 1 z+D 1 =0, A 2 x+B 2 y+C 2 z+D 2 = 0. Në mënyrë që rrafshi π 3, i përcaktuar në lidhje me PDSC nga ekuacioni i tij i përgjithshëm A 3 x+B 3 y+C 3 z+D 3 =0, t'i përkasë rrezes së formuar nga rrafshet π 1 dhe π 2, ai është e nevojshme dhe e mjaftueshme që ana e majte ekuacionet e rrafshit π 3 u paraqitën si një kombinim linear i anëve të majta të ekuacioneve të planeve π 1 dhe π 2.

10.Ekuacioni parametrik vektorial i një drejtëze në hapësirë:

ku është vektori i rrezes së një pike fikse M 0 i shtrirë në një vijë është një vektor jozero kolinear me këtë vijë, dhe është vektori i rrezes së një pike arbitrare në vijë.

Ekuacioni parametrik i një drejtëze në hapësirë:

M

Ekuacioni kanonik i drejtëzës në hapësirë:

ku janë koordinatat e ndonjë pike fikse M 0 shtrirë në një vijë të drejtë; - koordinatat e vektorit kolinear me këtë drejtëz.

Ekuacioni i përgjithshëm vektorial i një drejtëze në hapësirë:

Meqenëse një vijë e drejtë është kryqëzimi i dy rrafsheve të ndryshme joparalele, të përcaktuara përkatësisht nga ekuacionet e përgjithshme:

atëherë ekuacioni i drejtëzës mund të specifikohet nga sistemi i këtyre ekuacioneve:

Këndi ndërmjet vektorëve të drejtimit do të jetë e barabartë me këndin ndërmjet vijave të drejta. Këndi ndërmjet vektorëve gjendet duke përdorur produktin skalar. cosA=(ab)/IaI*IbI

Këndi ndërmjet vijës së drejtë dhe rrafshit gjendet me formulën:

Kushtet për paralelizmin e dy drejtëzave:

a) Nëse drejtëzat jepen nga ekuacionet (4) me një koeficient këndor, atëherë kushti i nevojshëm dhe i mjaftueshëm për paralelizmin e tyre është barazia e koeficientëve të tyre këndorë:

k 1 = k 2 . (8)

b) Për rastin kur drejtëzat jepen me ekuacione në pamje e përgjithshme(6), kusht i domosdoshëm dhe i mjaftueshëm për paralelizmin e tyre është që koeficientët për koordinatat e rrymës përkatëse në ekuacionet e tyre të jenë proporcionale, d.m.th.

Kushtet për pingulitetin e dy drejtëzave:

a) Në rastin kur drejtëzat jepen nga ekuacionet (4) me koeficient këndor, kusht i domosdoshëm dhe i mjaftueshëm për pingulitetin e tyre është që ato shpatet janë të anasjelltë në madhësi dhe të kundërta në shenjë, d.m.th.

b) Nëse ekuacionet e drejtëzave janë dhënë në formën e përgjithshme (6), atëherë kushti për pingulitetin e tyre (i domosdoshëm dhe i mjaftueshëm) është që të plotësojnë barazinë.

A 1 A 2 + B 1 B 2 = 0. (12)

Vija e drejtë quhet pingul me rrafshin, nëse është pingul me ndonjë drejtëz në këtë rrafsh. Nëse një drejtëz është pingul me secilën prej dy drejtëzave të kryqëzuara të një rrafshi, atëherë ajo është pingul me atë rrafsh. Që një drejtëz dhe një rrafsh të jenë paralele, është e nevojshme dhe e mjaftueshme që vektori normal me rrafshin dhe vektori i drejtimit të drejtëzës të jenë pingul. Për ta bërë këtë, është e nevojshme që produkti skalar i tyre të jetë i barabartë me zero.

Që një drejtëz dhe një rrafsh të jenë pingul, është e nevojshme dhe e mjaftueshme që vektori normal me rrafshin dhe vektori i drejtimit të drejtëzës të jenë kolinear. Ky kusht plotësohet nëse prodhimi vektorial i këtyre vektorëve ishte i barabartë me zero.

12. Në hapësirë, distanca nga një pikë në një vijë të caktuar ekuacioni parametrik

mund të gjendet si distanca minimale nga një pikë e caktuar në një pikë arbitrare në një vijë. Koeficient t kjo pikë mund të gjendet me formulën

Distanca midis vijave të kalimit quhet gjatësia e pingules së tyre të përbashkët. Është e barabartë me distancën midis planeve paralele që kalojnë nëpër këto vija.

Def. Sistemi i elementeve x 1,…,x m linear. pr-va V quhet linearisht i varur nëse ∃ λ 1 ,…, λ m ∈ ℝ (|λ 1 |+…+| λ m | ≠ 0) i tillë që λ 1 x 1 +…+ λ m x m = θ .

Def. Një sistem elementesh x 1 ,…,x m ∈ V quhet linearisht i pavarur nëse barazia λ 1 x 1 +…+ λ m x m = θ ⟹λ 1 =…= λ m =0.

Def. Një element x ∈ V quhet kombinim linear i elementeve x 1 ,…,x m ∈ V nëse ∃ λ 1 ,…, λ m ∈ ℝ i tillë që x= λ 1 x 1 +…+ λ m x m .

Teorema (kriteri i varësisë lineare): Një sistem vektorësh x 1 ,…,x m ∈ V është linearisht i varur nëse dhe vetëm nëse të paktën një vektor i sistemit shprehet në mënyrë lineare në terma të të tjerëve.

Doc. Domosdoshmëria: Le të jetë x 1 ,…,x m e varur linearisht ⟹ ∃ λ 1 ,…, λ m ∈ ℝ (| λ 1 |+…+| λ m | ≠ 0) e tillë që λ 1 x 1 +…+ λ m -1 x m -1 + λ m x m = θ. Le të themi λ m ≠ 0, atëherë

x m = (- ) x 1 +…+ (- ) x m -1.

Përshtatshmëria: Le të shprehet të paktën një nga vektorët në mënyrë lineare përmes vektorëve të mbetur: x m = λ 1 x 1 +…+ λ m -1 x m -1 (λ 1 ,…, λ m -1 ∈ ℝ) λ 1 x 1 + …+ λ m -1 x m -1 +(-1) x m =0 λ m =(-1) ≠ 0 ⟹ x 1 ,…,x m - linearisht i pavarur.

Ven. kushti i varësisë lineare:

Nëse një sistem përmban një element zero ose një nënsistem të varur linearisht, atëherë ai është i varur në mënyrë lineare.

λ 1 x 1 +…+ λ m x m = 0 – sistem i varur në mënyrë lineare

1) Le të jetë x 1 = θ, atëherë kjo barazi është e vlefshme për λ 1 =1 dhe λ 1 =…= λ m =0.

2) Le të jetë λ 1 x 1 +…+ λ m x m =0 – nënsistem i varur linear ⟹|λ 1 |+…+| λ m | ≠ 0 . Pastaj për λ 1 =0 marrim gjithashtu, |λ 1 |+…+| λ m | ≠ 0 ⟹ λ 1 x 1 +…+ λ m x m =0 – sistem i varur në mënyrë lineare.

Baza e hapësirës lineare. Koordinatat e vektorit në një bazë të caktuar. Koordinatat e shumave të vektorëve dhe prodhimit të një vektori dhe një numri. Një kusht i domosdoshëm dhe i mjaftueshëm për varësinë lineare të një sistemi vektorësh.

Përkufizimi: Një sistem i renditur i elementeve e 1, ..., e n të një hapësire lineare V quhet baza e kësaj hapësire nëse:

A) e 1 ... e n janë linearisht të pavarur

B) ∀ x ∈ α 1 … α n të tillë që x= α 1 e 1 +…+ α n e n

x= α 1 e 1 +…+ α n e n – zgjerimi i elementit x në bazën e 1, …, e n

α 1 … α n ∈ ℝ – koordinatat e elementit x në bazën e 1, …, e n

Teorema: Nëse në një hapësirë ​​lineare V është dhënë baza e 1, …, e n, atëherë ∀ x ∈ V kolona e koordinatave x në bazën e 1, …, e n përcaktohet në mënyrë unike (koordinatat përcaktohen në mënyrë unike)

Dëshmi: Le të x=α 1 e 1 +…+ α n e n dhe x=β 1 e 1 +…+β n e n

x= ⇔ = Θ, d.m.th. e 1, …, e n janë linearisht të pavarura, atëherë - =0 ∀ i=1, …, n ⇔ = ∀ i=1, …, n etj.

Teorema: le të jetë e 1, …, e n baza e hapësirës lineare V; x, y janë elemente arbitrare të hapësirës V, λ ∈ ℝ është një numër arbitrar. Kur shtohen x dhe y, koordinatat e tyre shtohen kur x shumëzohet me λ, shumëzohen edhe koordinatat x me λ.

Dëshmi: x= (e 1, …, e n) dhe y= (e 1, …, e n)

x+y= + = (e 1, …, e n)

λx= λ ) = (e 1, …, e n)

Lema 1: (kusht i domosdoshëm dhe i mjaftueshëm për varësinë lineare të një sistemi vektorësh)

Le të jetë e 1 …е n baza e hapësirës V. Një sistem elementësh f 1 , …, f k ∈ V është linearisht i varur nëse dhe vetëm nëse kolonat koordinative të këtyre elementeve në bazën e 1, …, e n janë varur në mënyrë lineare

Dëshmi: le të zgjerojmë f 1, …, f k sipas bazës e 1, …, e n

f m =(e 1, …, e n) m=1, …, k

λ 1 f 1 +…+λ k f k =(e 1, …, e n)[ λ 1 +…+ λ n ] domethënë, λ 1 f 1 +…+λ k f k = Θ ⇔

⇔ λ 1 +…+ λ n = cila është ajo që duhej vërtetuar.

13. Dimensioni i hapësirës lineare. Teorema mbi lidhjen ndërmjet dimensionit dhe bazës.
Përkufizimi: Hapësira lineare V quhet hapësirë ​​n-dimensionale nëse në V ka n elementë të pavarur linearisht dhe një sistem prej çdo n+1 elementi të hapësirës V është linearisht i varur. Në këtë rast, n quhet dimensioni i hapësirës lineare V dhe shënohet me dimV=n.

Një hapësirë ​​lineare quhet infinite-dimensionale nëse ∀N ∈ ℕ në hapësirën V ekziston një sistem linearisht i pavarur që përmban N elementë.

Teorema: 1) Nëse V është një hapësirë ​​lineare n-dimensionale, atëherë çdo sistem i renditur prej n elementësh linearisht të pavarur të kësaj hapësire përbën bazën. 2) Nëse në një hapësirë ​​lineare V ekziston një bazë e përbërë nga n elementë, atëherë dimensioni i V është i barabartë me n (dimV=n).

Dëshmi: 1) Le të dimV=n ⇒ në V ∃ n elemente linearisht të pavarur e 1, …, e n. Do të vërtetojmë se këta elementë përbëjnë një bazë, domethënë do të vërtetojmë se ∀ x ∈ V mund të zgjerohet në e 1, …, e n . Le t'u shtojmë x: e 1, ..., e n, x - ky sistem përmban n+1 vektorë, që do të thotë se është i varur në mënyrë lineare. Meqenëse e 1, …, e n është linearisht i pavarur, atëherë nga Teorema 2 x shprehur në mënyrë lineare përmes e 1, …, e n d.m.th. ∃ ,…, të tillë që x= α 1 e 1 +…+ α n e n . Pra e 1, …, e n është baza e hapësirës V. 2) Le të jetë e 1, …, e n baza e V, pra ka ∃ n elemente të pavarura linearisht në V. Le të marrim elemente arbitrare f 1 ,…,f n ,f n +1 ∈ V – n+1. Le të tregojmë varësinë e tyre lineare. Le t'i ndajmë ato sipas bazës së tyre:

f m =(e 1, …,e n) = ku m = 1,…,n Le të krijojmë një matricë të kolonave koordinative: A= Matrica përmban n rreshta ⇒ RgA≤n. Numri i kolonave n+1 > n ≥ RgA ⇒ Kolonat e matricës A (d.m.th., kolonat e koordinatave f 1 ,…,f n ,f n +1) janë të varura në mënyrë lineare. Nga Lema 1 ⇒ ,…,f n ,f n +1 varen në mënyrë lineare ⇒ dimV=n.

Pasoja: Nëse ndonjë bazë përmban n elementë, atëherë çdo bazë tjetër në këtë hapësirë ​​përmban n elementë.

Teorema 2: Nëse sistemi i vektorëve x 1 ,… ,x m -1 , x m është i varur në mënyrë lineare, dhe nënsistemi i tij x 1 ,… ,x m -1 është linearisht i pavarur, atëherë x m shprehet në mënyrë lineare përmes x 1 ,… ,x m -1

Dëshmi: Sepse x 1 ,… ,x m -1 , x m është linearisht i varur, atëherë ∃ , …, , ,

, …, | , | sikurse . Nëse , , …, | => x 1 ,… ,x m -1 – janë linearisht të pavarura, të cilat nuk mund të jenë. Kjo do të thotë m = (- ) x 1 +…+ (- ) x m -1.