Natuurlijke logaritme, functie ln x. Logaritme
De basiseigenschappen van de natuurlijke logaritme, grafiek, definitiedomein, reeks waarden, basisformules, afgeleide, integraal, uitbreiding van machtreeksen en weergave van de functie ln x met behulp van complexe getallen worden gegeven.
Definitie
Natuurlijke logaritme is de functie y = In x, het omgekeerde van het exponentiële, x = e y, en is de logaritme met de basis van het getal e: ln x = log e x.
De natuurlijke logaritme wordt veel gebruikt in de wiskunde omdat de afgeleide ervan de eenvoudigste vorm heeft: (lnx)′ = 1/x.
Gebaseerd op definities, is de basis van de natuurlijke logaritme het getal e:
e ≅ 2,718281828459045...;
.

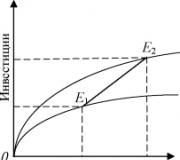
Grafiek van de functie y = In x.
Grafiek van natuurlijke logaritme (functies y = In x) wordt verkregen uit de exponentiële grafiek spiegelbeeld ten opzichte van de rechte lijn y = x.
De natuurlijke logaritme wordt gedefinieerd voor positieve waarden van de variabele x.
Het neemt monotoon toe in zijn domein van definitie. 0 Bij x →
de limiet van de natuurlijke logaritme is minus oneindig (-∞).
Als x → + ∞ is de limiet van de natuurlijke logaritme plus oneindig (+ ∞). Voor grote x neemt de logaritme vrij langzaam toe. Elke machtsfunctie x a met een positieve exponent a groeit sneller dan de logaritme.
Eigenschappen van de natuurlijke logaritme
Domein van definitie, reeks waarden, extrema, toename, afname
De natuurlijke logaritme is een monotoon stijgende functie en heeft dus geen extremen. De belangrijkste eigenschappen van de natuurlijke logaritme worden weergegeven in de tabel.
In x-waarden
In 1 = 0
Basisformules voor natuurlijke logaritmes
Formules die volgen uit de definitie van de inverse functie:
De belangrijkste eigenschap van logaritmen en de gevolgen ervan
Basisvervangingsformule
Elke logaritme kan worden uitgedrukt in termen van natuurlijke logaritmen met behulp van de basissubstitutieformule:
Bewijzen van deze formules worden gepresenteerd in de sectie "Logaritme".
Inverse functie
De inverse van de natuurlijke logaritme is de exponent.
Als, dan
Als, dan.
Afgeleide ln x
.
Afgeleide van de natuurlijke logaritme:
.
Afgeleide van de natuurlijke logaritme van modulus x:
.
Afgeleide van de n-de orde:
Formules afleiden > > >
Integraal
.
De integraal wordt berekend door integratie in delen:
Dus,
Uitdrukkingen waarbij gebruik wordt gemaakt van complexe getallen
.
Beschouw de functie van de complexe variabele z: Laten we de complexe variabele uitdrukken z via module R φ
:
.
en betoog
.
Met behulp van de eigenschappen van de logaritme hebben we:
.
Of
Het argument φ is niet uniek gedefinieerd. Als je zet
het zal hetzelfde getal zijn voor verschillende n.
Daarom is de natuurlijke logaritme, als functie van een complexe variabele, geen functie met één waarde.
Uitbreiding van de machtreeksen
Wanneer de uitbreiding plaatsvindt:
Gebruikte literatuur:
IN. Bronstein, K.A. Semendyaev, Handboek wiskunde voor ingenieurs en studenten, “Lan”, 2009.
Natuurlijke logaritme
Grafiek van de natuurlijke logaritmefunctie. De functie nadert langzaam de positieve oneindigheid naarmate deze groter wordt X en benadert snel de negatieve oneindigheid wanneer X neigt naar 0 (“langzaam” en “snel” vergeleken met welke vermogensfunctie dan ook X).
Natuurlijke logaritme is de logaritme ten opzichte van de basis , Waar e- een irrationele constante gelijk aan ongeveer 2,718281 828. De natuurlijke logaritme wordt gewoonlijk geschreven als ln( X), log e (X) of soms gewoon inloggen( X), als de basis e impliciet.
Natuurlijke logaritme van een getal X(geschreven als ln(x)) is de exponent waarmee het getal moet worden verhoogd e te krijgen X. Bijvoorbeeld, ln(7.389...) is gelijk aan 2 omdat e 2 =7,389... . Natuurlijke logaritme van het getal zelf e (ln(e)) is gelijk aan 1 omdat e 1 = e, en de natuurlijke logaritme is 1 ( ln(1)) is gelijk aan 0 omdat e 0 = 1.
De natuurlijke logaritme kan voor elk positief reëel getal worden gedefinieerd A als het gebied onder de curve j = 1/X van 1 tot A. De eenvoud van deze definitie, die consistent is met veel andere formules die de natuurlijke logaritme gebruiken, leidde tot de naam "natuurlijk". Deze definitie kan worden uitgebreid tot complexe getallen, zoals hieronder besproken.
Als we de natuurlijke logaritme beschouwen als een reële functie van een reële variabele, dan is het de inverse functie van de exponentiële functie, die tot de identiteiten leidt:
Zoals alle logaritmen, wijst de natuurlijke logaritme vermenigvuldiging toe aan optelling:
De logaritmische functie is dus een isomorfisme van de groep positieve reële getallen met betrekking tot vermenigvuldiging door de groep reële getallen met betrekking tot optelling, die kan worden weergegeven als een functie:
De logaritme kan worden gedefinieerd voor elke positieve grondtal anders dan 1, niet alleen e, maar logaritmen voor andere basen verschillen alleen van de natuurlijke logaritme door een constante factor, en worden gewoonlijk gedefinieerd in termen van de natuurlijke logaritme. Logaritmen zijn handig voor het oplossen van vergelijkingen waarbij onbekenden als exponenten voorkomen. Logaritmen worden bijvoorbeeld gebruikt om de vervalconstante voor een bekende halfwaardetijd te vinden, of om de vervaltijd te vinden bij het oplossen van radioactiviteitsproblemen. Ze spelen een belangrijke rol op veel gebieden van de wiskunde en toegepaste wetenschappen, en worden in de financiële wereld gebruikt om veel problemen op te lossen, waaronder het vinden van samengestelde rente.
Verhaal
De eerste vermelding van de natuurlijke logaritme werd gemaakt door Nicholas Mercator in zijn werk Logaritmotechniek, gepubliceerd in 1668, hoewel wiskundeleraar John Spidell in 1619 een tabel met natuurlijke logaritmen samenstelde. Het werd voorheen de hyperbolische logaritme genoemd omdat het overeenkomt met het gebied onder de hyperbool. Het wordt soms de Napier-logaritme genoemd, hoewel de oorspronkelijke betekenis van deze term enigszins anders was.
Aanwijzingsconventies
De natuurlijke logaritme wordt gewoonlijk aangegeven met “ln( X)", logaritme met grondtal 10 - via "lg( X)", en andere redenen worden meestal expliciet aangegeven met het symbool "log".
In veel werken over discrete wiskunde, cybernetica en informatica gebruiken auteurs de notatie “log( X)" voor logaritmen met grondtal 2, maar deze conventie wordt niet algemeen aanvaard en vereist verduidelijking in de lijst met gebruikte notaties of (bij gebrek aan een dergelijke lijst) door een voetnoot of commentaar bij het eerste gebruik.
Haakjes rond het argument van logaritmen (als dit niet leidt tot een foutieve lezing van de formule) worden meestal weggelaten, en bij het verheffen van een logaritme tot een macht wordt de exponent direct toegewezen aan het teken van de logaritme: ln 2 ln 3 4 X 5 = [ ln ( 3 )] 2 .
Anglo-Amerikaans systeem
Wiskundigen, statistici en sommige ingenieurs gebruiken gewoonlijk de term ‘natuurlijke logaritme’ of ‘log( X)" of "ln( X)", en om de logaritme met grondtal 10 aan te duiden - "log 10 ( X)».
Sommige ingenieurs, biologen en andere specialisten schrijven altijd “ln( X)" (of af en toe "log e ( X)") wanneer ze de natuurlijke logaritme bedoelen, en de notatie "log( X)" ze bedoelen log 10 ( X).
loggen e is een "natuurlijke" logaritme omdat deze automatisch voorkomt en heel vaak voorkomt in de wiskunde. Beschouw bijvoorbeeld het probleem van de afgeleide van een logaritmische functie:
Als de basis B gelijk aan e, dan is de afgeleide eenvoudigweg 1/ X, en wanneer X= 1 Deze afgeleide is gelijk aan 1. Nog een reden waarom de basis e Het meest natuurlijke aan de logaritme is dat deze heel eenvoudig kan worden gedefinieerd in termen van een eenvoudige integraal of Taylorreeks, wat niet kan worden gezegd over andere logaritmes.
Verdere rechtvaardigingen voor natuurlijkheid houden geen verband met de notatie. Er zijn bijvoorbeeld verschillende eenvoudige reeksen met natuurlijke logaritmen. Pietro Mengoli en Nicholas Mercator noemden ze logaritme naturalis enkele decennia totdat Newton en Leibniz differentiaal- en integraalrekening ontwikkelden.
Definitie
Formeel ln( A) kan worden gedefinieerd als het gebied onder de curve van grafiek 1/ X van 1 tot A, dat wil zeggen als een integraal:
Het is echt een logaritme omdat het voldoet aan de fundamentele eigenschap van de logaritme:
Dit kan worden aangetoond door het volgende aan te nemen:
Numerieke waarde
Om de numerieke waarde van de natuurlijke logaritme van een getal te berekenen, kun je de Taylorreeksuitbreiding in de vorm gebruiken:
Om te krijgen betere snelheid convergentie kunnen we de volgende identiteit gebruiken:
Voor ln( X), Waar X> 1 dan dichter waarde X tot 1, hoe sneller de convergentiesnelheid. De identiteiten die aan de logaritme zijn gekoppeld, kunnen worden gebruikt om het doel te bereiken:
Deze methoden werden al vóór de komst van rekenmachines gebruikt, waarvoor numerieke tabellen werden gebruikt en manipulaties werden uitgevoerd die vergelijkbaar waren met die hierboven beschreven.
Hoge nauwkeurigheid
Om de natuurlijke logaritme te berekenen met een groot aantal nauwkeurigheidsgetallen is de Taylor-reeks niet efficiënt omdat de convergentie langzaam is. Een alternatief is om de methode van Newton te gebruiken om te inverteren naar een exponentiële functie waarvan de reeks sneller convergeert.
Een alternatief voor een zeer hoge rekennauwkeurigheid is de formule:
Waar M geeft het rekenkundig-geometrische gemiddelde van 1 en 4/s aan, en
M zo gekozen P nauwkeurigheidskenmerken worden bereikt. (In de meeste gevallen is een waarde van 8 voor m voldoende.) Als deze methode wordt gebruikt, kan Newtons inverse van de natuurlijke logaritme worden toegepast om de exponentiële functie efficiënt te berekenen. (De constanten ln 2 en pi kunnen vooraf worden berekend tot de gewenste nauwkeurigheid met behulp van een van de bekende snel convergente reeksen.)
Computationele complexiteit
De computationele complexiteit van natuurlijke logaritmen (met behulp van het rekenkundig-geometrische gemiddelde) is O( M(N)ln N). Hier N is het aantal precisiecijfers waarvoor de natuurlijke logaritme moet worden geëvalueerd, en M(N) is de computationele complexiteit van het vermenigvuldigen van twee N-cijfers.
Vervolg breuken
Hoewel er geen eenvoudige kettingbreuken zijn die een logaritme weergeven, kunnen er verschillende gegeneraliseerde kettingbreuken worden gebruikt, waaronder:
Complexe logaritmen
De exponentiële functie kan worden uitgebreid tot een functie die een complex getal van de vorm geeft e X voor elk willekeurig complex getal X, in dit geval een oneindige reeks met complex X. Deze exponentiële functie kan worden omgekeerd om een complexe logaritme te vormen, die de meeste eigenschappen van gewone logaritmes zal hebben. Er zijn echter twee problemen: die is er niet X, waarvoor e X= 0, en dat blijkt e 2πi = 1 = e 0 . Omdat de multiplicativiteitseigenschap dus geldig is voor een complexe exponentiële functie e Laten we de complexe variabele uitdrukken = e Laten we de complexe variabele uitdrukken+2nπi voor alle complexen Laten we de complexe variabele uitdrukken en heel N.
De logaritme kan niet over het hele complexe vlak worden gedefinieerd, en toch heeft hij meerdere waarden - elke complexe logaritme kan worden vervangen door een "equivalente" logaritme door een geheel veelvoud van 2 toe te voegen πi. De complexe logaritme kan alleen op een segment van het complexe vlak worden gewaardeerd. Bijvoorbeeld, ln i = 1/2 πi of 5/2 πi of −3/2 πi, enz., en hoewel i 4 = 1,4 logboek i kan worden gedefinieerd als 2 πi, of 10 πi of −6 πi, enzovoort.

Zie ook
- John Napier - uitvinder van logaritmen
Opmerkingen
- Wiskunde voor fysische chemie. - 3e. - Academic Press, 2005. - P. 9. - ISBN 0-125-08347-5,Uittreksel van pagina 9
- JJO"Connor en EF Robertson Het nummer e. Het MacTutor History of Mathematics-archief (september 2001). Gearchiveerd
- Cajori Florian Een geschiedenis van de wiskunde, 5e druk. - AMS Boekhandel, 1991. - P. 152. - ISBN 0821821024
- Flitsman, Martin Integralen schatten met behulp van polynomen. Gearchiveerd van het origineel op 12 februari 2012.
Dit kan bijvoorbeeld een rekenmachine zijn uit de basisset van operatiekamerprogramma's Windows-systemen. De link om het te starten is behoorlijk verborgen in het hoofdmenu van het besturingssysteem - open het door op de knop "Start" te klikken, open vervolgens het gedeelte "Programma's", ga naar de subsectie "Standaard" en vervolgens naar de "Hulpprogramma's" sectie en klik ten slotte op het item "Rekenmachine" " In plaats van de muis te gebruiken en door menu's te navigeren, kunt u het toetsenbord en het programmastartdialoogvenster gebruiken - druk op de WIN + R-toetscombinatie, typ calc (dit is de naam van het uitvoerbare bestand van de rekenmachine) en druk op Enter.
Schakel de rekenmachineinterface naar de geavanceerde modus, waarmee u... Standaard wordt het geopend in de “normale” weergave, maar je hebt “engineering” of “ ” nodig (afhankelijk van de versie van het besturingssysteem dat je gebruikt). Vouw het gedeelte "Beeld" in het menu uit en selecteer de juiste regel.
Voer het argument in waarvan u de natuurlijke waarde wilt evalueren. Dit kan gedaan worden vanaf het toetsenbord of door op de overeenkomstige knoppen in de rekenmachine-interface op het scherm te klikken.
Klik op de knop met het label ln - het programma berekent de logaritme met grondtal e en toont het resultaat.
Gebruik een van de -rekenmachines als alternatief voor het berekenen van de waarde van de natuurlijke logaritme. Bijvoorbeeld degene die zich bevindt op http://calc.org.ua. De interface is uiterst eenvoudig: er is één invoerveld waarin u de waarde van het getal moet typen, waarvan u de logaritme moet berekenen. Zoek tussen de knoppen de knop met de tekst ln. Het script van deze rekenmachine vereist geen verzending van gegevens naar de server en een antwoord, dus u ontvangt het berekeningsresultaat vrijwel onmiddellijk. Het enige kenmerk waarmee rekening moet worden gehouden, is dat het scheidingsteken tussen de breuken en gehele delen van het ingevoerde getal een punt moet zijn, en niet .
De term " logaritme" komt van twee Griekse woorden, waarvan het ene 'getal' betekent en het andere 'verhouding'. Het duidt de wiskundige bewerking aan van het berekenen van een variabele grootheid (exponent) waartoe een constante waarde (basis) moet worden verhoogd om het getal te verkrijgen dat wordt aangegeven onder het teken logaritme A. Als de basis gelijk is aan een wiskundige constante die het getal "e" wordt genoemd, dan logaritme‘natuurlijk’ genoemd.
Je zult nodig hebben
- Internettoegang, Microsoft Office Excel of rekenmachine.
Instructies
Gebruik de vele rekenmachines die op internet beschikbaar zijn. Dit is misschien een gemakkelijke manier om natuurlijke a te berekenen. U hoeft niet naar de juiste dienst te zoeken, aangezien er veel zijn zoekmachines en hebben zelf ingebouwde rekenmachines, heel geschikt om mee te werken logaritme vriend. Ga bijvoorbeeld naar de hoofdpagina van de grootste online zoekmachine: Google. Er zijn hier geen knoppen nodig voor het invoeren van waarden of het selecteren van functies, typ gewoon de gewenste in het verzoekinvoerveld wiskundige bewerking. Laten we zeggen, om te berekenen logaritme en het getal 457 in basis “e”, voer ln 457 in - dit is voldoende voor Google om weer te geven met een nauwkeurigheid van acht decimalen (6,12468339), zelfs zonder op de knop te drukken om een verzoek naar de server te sturen.
Gebruik de juiste ingebouwde functie als u de waarde van een natuurlijk getal wilt berekenen logaritme en treedt op bij het werken met gegevens in de populaire spreadsheet-editor Microsoft Office Excel. Deze functie wordt hier aangeroepen met de gebruikelijke notatie logaritme en in hoofdletters - LN. Selecteer de cel waarin het berekeningsresultaat moet worden weergegeven en voer een gelijkteken in - zo moeten in deze spreadsheet-editor de records beginnen in de cellen in de subsectie "Standaard" van de sectie "Alle programma's" van het hoofdmenu. Schakel de rekenmachine naar een meer functionele modus door op de sneltoets Alt + 2 te drukken. Voer vervolgens de waarde in, natuurlijk logaritme die u wilt berekenen, en klik in de programma-interface op de knop aangegeven door de symbolen ln. De applicatie voert de berekening uit en geeft het resultaat weer.
Video over het onderwerp
De logaritme van een positief getal b met grondtal a (a>0, a is niet gelijk aan 1) is een getal c zodat a c = b: log a b = c ⇔ a c = b (a > 0, a ≠ 1, b > 0)
Merk op dat de logaritme van een niet-positief getal niet gedefinieerd is. Bovendien moet de basis van de logaritme een positief getal zijn dat niet gelijk is aan 1. Als we bijvoorbeeld -2 kwadrateren, krijgen we het getal 4, maar dit betekent niet dat de logaritme met grondtal -2 van 4 gelijk is naar 2.
Fundamentele logaritmische identiteit
a log a b = b (a > 0, a ≠ 1) (2)Het is belangrijk dat de reikwijdte van de definitie van de rechter- en linkerkant van deze formule verschillend is. Linkerkant is alleen gedefinieerd voor b>0, a>0 en a ≠ 1. De rechterkant is gedefinieerd voor elke b en is helemaal niet afhankelijk van a. De toepassing van de fundamentele logaritmische ‘identiteit’ bij het oplossen van vergelijkingen en ongelijkheden kan dus leiden tot een verandering in de OD.
Twee voor de hand liggende gevolgen van de definitie van logaritme
log a a = 1 (a > 0, a ≠ 1) (3)log a 1 = 0 (a > 0, a ≠ 1) (4)
Als we het getal a tot de eerste macht verheffen, krijgen we hetzelfde getal, en als we het tot de macht nul verheffen, krijgen we er één.
Logaritme van het product en logaritme van het quotiënt
log a (bc) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) (5)Log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0) (6)
Ik wil schoolkinderen waarschuwen voor het gedachteloos gebruik van deze formules bij het oplossen van logaritmische vergelijkingen en ongelijkheden. Als je ze ‘van links naar rechts’ gebruikt, wordt de ODZ smaller, en als je van de som of het verschil van logaritmen naar de logaritme van het product of quotiënt gaat, wordt de ODZ groter.
De uitdrukking log a (f (x) g (x)) wordt in twee gevallen gedefinieerd: wanneer beide functies strikt positief zijn of wanneer f(x) en g(x) beide kleiner zijn dan nul.
Als we deze uitdrukking transformeren in de som log a f (x) + log a g (x), zijn we gedwongen ons alleen te beperken tot het geval waarin f(x)>0 en g(x)>0. Er is sprake van een vernauwing van het bereik van aanvaardbare waarden, en dit is categorisch onaanvaardbaar, omdat dit kan leiden tot het verlies van oplossingen. Een soortgelijk probleem bestaat voor formule (6).
De graad kan uit het teken van de logaritme worden gehaald
log a b p = p log a b (a > 0, a ≠ 1, b > 0) (7)En opnieuw zou ik willen oproepen tot nauwkeurigheid. Beschouw het volgende voorbeeld:
Log a (f (x) 2 = 2 log a f (x)
De linkerkant van de gelijkheid is uiteraard gedefinieerd voor alle waarden van f(x) behalve nul. De rechterkant is alleen voor f(x)>0! Door de graad uit de logaritme te halen, verkleinen we de ODZ opnieuw. De omgekeerde procedure leidt tot een uitbreiding van het bereik van aanvaardbare waarden. Al deze opmerkingen gelden niet alleen voor macht 2, maar ook voor elke even macht.
Formule voor het verhuizen naar een nieuwe stichting
log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1) (8)Dat zeldzame geval waarin de ODZ niet verandert tijdens transformatie. Als je basis c verstandig hebt gekozen (positief en niet gelijk aan 1), is de formule voor het verhuizen naar een nieuwe basis volkomen veilig.
Als we het getal b als de nieuwe grondtal c kiezen, krijgen we een belangrijk getal speciaal geval formules (8):
Log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) (9)
Enkele eenvoudige voorbeelden met logaritmen
Voorbeeld 1. Bereken: log2 + log50.
Oplossing. log2 + log50 = log100 = 2. We gebruikten de som van de logaritmes-formule (5) en de definitie van de decimale logaritme.
Voorbeeld 2. Bereken: lg125/lg5.
Oplossing. log125/log5 = log 5 125 = 3. We gebruikten de formule voor het verplaatsen naar een nieuwe basis (8).
Tabel met formules gerelateerd aan logaritmen
| a log a b = b (a > 0, a ≠ 1) |
| log a a = 1 (a > 0, a ≠ 1) |
| log a 1 = 0 (a > 0, a ≠ 1) |
| log a (bc) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) |
| log a b c = log a b - log a c (a > 0, a ≠ 1, b > 0, c > 0) |
| log a b p = p log a b (a > 0, a ≠ 1, b > 0) |
| log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1) |
| log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) |
Zoals je weet, tellen bij het vermenigvuldigen van uitdrukkingen met machten de exponenten altijd op (a b *a c = a b+c). Deze wiskundige wet werd afgeleid door Archimedes, en later, in de 8e eeuw, creëerde de wiskundige Virasen een tabel met gehele exponenten. Zij waren het die dienden voor de verdere ontdekking van logaritmen. Voorbeelden van het gebruik van deze functie zijn bijna overal te vinden waar u lastige vermenigvuldiging moet vereenvoudigen door eenvoudig optellen. Als u dit artikel 10 minuten leest, leggen wij u uit wat logaritmen zijn en hoe u ermee kunt werken. In eenvoudige en toegankelijke taal.
Definitie in de wiskunde
Een logaritme is een uitdrukking van de volgende vorm: log a b=c, dat wil zeggen de logaritme van elk niet-negatief getal (dat wil zeggen elk positief getal) “b” tot zijn grondtal “a” wordt beschouwd als de macht “c ” Waartoe het nodig is om de basis “a” te verhogen om uiteindelijk de waarde “b” te krijgen. Laten we de logaritme analyseren met behulp van voorbeelden, laten we zeggen dat er een uitdrukking log 2 8 is. Hoe vind je het antwoord? Het is heel eenvoudig, je moet een macht vinden zodat je van 2 tot de vereiste macht 8 krijgt. Na wat berekeningen in je hoofd te hebben gedaan, krijgen we het getal 3! En dat is waar, want 2 tot de macht 3 geeft het antwoord 8.
Soorten logaritmen
Voor veel leerlingen en studenten lijkt dit onderwerp ingewikkeld en onbegrijpelijk, maar in feite zijn logaritmen niet zo eng, het belangrijkste is om hun algemene betekenis te begrijpen en hun eigenschappen en enkele regels te onthouden. Er zijn drie afzonderlijke typen logaritmische uitdrukkingen:
- Natuurlijke logaritme ln a, waarbij de basis het Eulergetal is (e = 2,7).
- Decimaal a, waarbij het grondtal 10 is.
- Logaritme van elk getal b met grondtal a>1.
Elk van hen wordt op een standaardmanier opgelost, inclusief vereenvoudiging, reductie en daaropvolgende reductie tot een enkele logaritme met behulp van logaritmische stellingen. Om de juiste waarden van logaritmen te verkrijgen, moet u hun eigenschappen en de volgorde van acties onthouden bij het oplossen ervan.
Regels en enkele beperkingen
In de wiskunde zijn er verschillende regels en beperkingen die als axioma worden aanvaard, dat wil zeggen dat ze niet ter discussie staan en de waarheid zijn. Het is bijvoorbeeld onmogelijk om getallen door nul te delen, en het is ook onmogelijk om de even wortel van negatieve getallen te extraheren. Logaritmen hebben ook hun eigen regels, waardoor u gemakkelijk kunt leren werken, zelfs met lange en ruime logaritmische uitdrukkingen:
- De grondtal “a” moet altijd groter zijn dan nul, en niet gelijk aan 1, anders verliest de uitdrukking zijn betekenis, omdat “1” en “0” in welke mate dan ook altijd gelijk zijn aan hun waarden;
- als a > 0, dan a b >0, dan blijkt dat “c” ook groter moet zijn dan nul.
Hoe logaritmes op te lossen?
De taak wordt bijvoorbeeld gegeven om het antwoord te vinden op de vergelijking 10 x = 100. Dit is heel eenvoudig, je moet een macht kiezen door het getal tien te verhogen tot waar we 100 krijgen. Dit is natuurlijk 10 2 = 100.
Laten we deze uitdrukking nu in logaritmische vorm weergeven. We krijgen log 10 100 = 2. Bij het oplossen van logaritmen komen alle acties praktisch samen om de macht te vinden waarvoor het nodig is om de basis van de logaritme in te voeren om een bepaald getal te verkrijgen.
Om de waarde nauwkeurig te bepalen onbekende graad je moet leren werken met de gradentabel. Het ziet er zo uit:

Zoals u kunt zien, kunnen sommige exponenten intuïtief worden geraden als u over een technische geest en kennis van de tafel van vermenigvuldiging beschikt. Voor grotere waarden heeft u echter een vermogenstabel nodig. Het kan zelfs worden gebruikt door degenen die helemaal niets van complex weten wiskundige onderwerpen. De linkerkolom bevat getallen (grondtal a), de bovenste rij getallen is de waarde van de macht c waartoe het getal a wordt verheven. Op het snijpunt bevatten de cellen de getalswaarden die het antwoord vormen (a c =b). Laten we bijvoorbeeld de allereerste cel met het getal 10 nemen en deze kwadrateren, we krijgen de waarde 100, die wordt aangegeven op het snijpunt van onze twee cellen. Alles is zo eenvoudig en gemakkelijk dat zelfs de meest ware humanist het zal begrijpen!
Vergelijkingen en ongelijkheden
Het blijkt dat onder bepaalde omstandigheden de exponent de logaritme is. Daarom kunnen alle wiskundige numerieke uitdrukkingen worden geschreven als een logaritmische gelijkheid. 3 4 =81 kan bijvoorbeeld worden geschreven als de logaritme met grondtal 3 van 81 gelijk aan vier (log 3 81 = 4). Voor negatieve machten zijn de regels hetzelfde: 2 -5 = 1/32, we schrijven het als een logaritme, we krijgen log 2 (1/32) = -5. Een van de meest fascinerende onderdelen van de wiskunde is het onderwerp ‘logaritmen’. We zullen hieronder naar voorbeelden en oplossingen van vergelijkingen kijken, onmiddellijk nadat we hun eigenschappen hebben bestudeerd. Laten we nu eens kijken hoe ongelijkheden eruit zien en hoe we ze van vergelijkingen kunnen onderscheiden.

De volgende uitdrukking wordt gegeven: log 2 (x-1) > 3 - het is een logaritmische ongelijkheid, aangezien de onbekende waarde "x" onder het logaritmische teken staat. En ook in de uitdrukking worden twee grootheden vergeleken: de logaritme van het gewenste getal met grondtal twee is groter dan het getal drie.
Het belangrijkste verschil tussen logaritmische vergelijkingen en ongelijkheden is dat vergelijkingen met logaritmen (bijvoorbeeld de logaritme 2 x = √9) een of meer specifieke antwoorden impliceren. numerieke waarden, terwijl bij het oplossen van de ongelijkheid zowel het bereik van toegestane waarden als de breekpunten van deze functie worden bepaald. Als gevolg hiervan is het antwoord niet een eenvoudige reeks individuele getallen, zoals bij het antwoord op een vergelijking, maar een continue reeks of reeks getallen.

Basisstellingen over logaritmen
Bij het oplossen van primitieve taken voor het vinden van de waarden van de logaritme, zijn de eigenschappen ervan mogelijk niet bekend. Als het echter om logaritmische vergelijkingen of ongelijkheden gaat, is het allereerst noodzakelijk om alle basiseigenschappen van logaritmen duidelijk te begrijpen en in de praktijk toe te passen. We zullen later naar voorbeelden van vergelijkingen kijken; laten we eerst elke eigenschap in meer detail bekijken.
- De hoofdidentiteit ziet er als volgt uit: a logaB =B. Het is alleen van toepassing als a groter is dan 0, niet gelijk aan één, en B groter is dan nul.
- De logaritme van het product kan worden weergegeven in de volgende formule: log d (s 1 * s 2) = log d s 1 + log d s 2. In dit geval is de verplichte voorwaarde: d, s 1 en s 2 > 0; a≠1. Je kunt een bewijs geven voor deze logaritmische formule, met voorbeelden en oplossing. Laten we log a s 1 = f 1 en log a s 2 = f 2, dan a f1 = s 1, a f2 = s 2. We verkrijgen dat s 1 * s 2 = a f1 *a f2 = a f1+f2 (eigenschappen van graden ), en dan per definitie: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2, en dat is wat bewezen moest worden.
- De logaritme van het quotiënt ziet er als volgt uit: log a (s 1/ s 2) = log a s 1 - log a s 2.
- De stelling in de vorm van een formule heeft de volgende vorm: log a q b n = n/q log a b.
Deze formule wordt de ‘eigenschap van de mate van logaritme’ genoemd. Het lijkt op de eigenschappen van gewone graden, en dat is niet verrassend, omdat alle wiskunde gebaseerd is op natuurlijke postulaten. Laten we naar het bewijs kijken.
Laten we log a b = t, dan blijkt a t = b. Als we beide delen verheffen tot de macht m: a tn = b n ;
maar aangezien a tn = (a q) nt/q = b n, dus log a q b n = (n*t)/t, log dan a q b n = n/q log a b. De stelling is bewezen.
Voorbeelden van problemen en ongelijkheden
De meest voorkomende soorten problemen met logaritmen zijn voorbeelden van vergelijkingen en ongelijkheden. Ze zijn te vinden in bijna alle probleemboeken en zijn ook een verplicht onderdeel van wiskunde-examens. Om naar een universiteit te gaan of toelatingsexamens in de wiskunde te behalen, moet je weten hoe je dergelijke taken correct kunt oplossen.

Helaas bestaat er geen enkel plan of schema voor het oplossen en bepalen van de onbekende waarde van de logaritme, maar het kan worden toegepast op elke wiskundige ongelijkheid of logaritmische vergelijking bepaalde regels. Allereerst moet u uitzoeken of de uitdrukking kan worden vereenvoudigd of waartoe deze kan leiden algemene uitstraling. U kunt lange logaritmische uitdrukkingen vereenvoudigen als u hun eigenschappen correct gebruikt. Laten we ze snel leren kennen.
Bij het oplossen van logaritmische vergelijkingen moeten we bepalen welk type logaritme we hebben: een voorbeelduitdrukking kan een natuurlijke logaritme of een decimale logaritme bevatten.
Hier zijn voorbeelden ln100, ln1026. Hun oplossing komt neer op het feit dat ze de macht moeten bepalen waarbij het grondtal 10 respectievelijk gelijk is aan 100 en 1026. Om natuurlijke logaritmen op te lossen, moet u logaritmische identiteiten of hun eigenschappen toepassen. Laten we eens kijken naar voorbeelden van het oplossen van logaritmische problemen van verschillende typen.

Logaritmeformules gebruiken: met voorbeelden en oplossingen
Laten we dus eens kijken naar voorbeelden van het gebruik van de basisstellingen over logaritmen.
- De eigenschap van de logaritme van een product kan worden gebruikt bij taken waarbij uitbreiding nodig is grote waarde getallen b in eenvoudiger factoren. Bijvoorbeeld log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Het antwoord is 9.
- log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - zoals je kunt zien, zijn we er met behulp van de vierde eigenschap van de logaritmemacht in geslaagd een ogenschijnlijk complexe en onoplosbare uitdrukking op te lossen. U hoeft alleen maar de grondtal in factoren te ontbinden en vervolgens de exponentwaarden uit het teken van de logaritme te halen.

Opdrachten van het Unified State Exam
Logaritmen worden vaak aangetroffen in toelatingsexamens, vooral veel logaritmische problemen bij het Unified State Exam (staatsexamen voor alle afgestudeerden). Doorgaans zijn deze taken niet alleen aanwezig in deel A (het gemakkelijkste testgedeelte van het examen), maar ook in deel C (de meest complexe en omvangrijke taken). Het examen vereist nauwkeurige en perfecte kennis van het onderwerp “Natuurlijke logaritmes”.
Voorbeelden en oplossingen voor problemen zijn afkomstig uit de officiële versie Unified State Exam-opties. Laten we eens kijken hoe dergelijke taken worden opgelost.
Gegeven log 2 (2x-1) = 4. Oplossing:
laten we de uitdrukking herschrijven, een beetje log 2 (2x-1) = 2 2 vereenvoudigen, door de definitie van de logaritme krijgen we dat 2x-1 = 2 4, dus 2x = 17; x = 8,5.
- Het is het beste om alle logaritmen tot hetzelfde grondtal terug te brengen, zodat de oplossing niet omslachtig en verwarrend wordt.
- Alle uitdrukkingen onder het logaritmeteken worden als positief aangegeven. Wanneer de exponent van een uitdrukking die onder het logaritmeteken staat en als grondtal als vermenigvuldiger wordt verwijderd, moet de uitdrukking die onder de logaritme overblijft dus positief zijn.