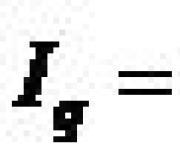Metoda e katrorëve më të vegjël është ndërtuar mbi kushtin. Ku aplikohet metoda e katrorëve më të vegjël?
Metoda e katrorëve më të vegjël është një nga më të zakonshmet dhe më të zhvilluarat për shkak të saj thjeshtësia dhe efikasiteti i metodave për vlerësimin e parametrave të lineare. Në të njëjtën kohë, duhet të kihet kujdes gjatë përdorimit të tij, pasi modelet e ndërtuara duke e përdorur atë mund të mos plotësojnë një sërë kërkesash për cilësinë e parametrave të tyre dhe, si rezultat, jo "mirë" pasqyrojnë modelet e zhvillimit të procesit.
Le të shqyrtojmë më në detaje procedurën për vlerësimin e parametrave të një modeli ekonometrik linear duke përdorur metodën e katrorëve më të vegjël. Një model i tillë në formë të përgjithshme mund të përfaqësohet nga ekuacioni (1.2):
y t = a 0 + a 1 x 1 t +...+ a n x nt + ε t .
Të dhënat fillestare kur vlerësohen parametrat a 0, a 1,..., a n është vektori i vlerave të ndryshores së varur y= (y 1 , y 2 , ... , y T)" dhe matricën e vlerave të variablave të pavarur

në të cilën kolona e parë, e përbërë nga një, korrespondon me koeficientin e modelit.
Metoda e katrorëve më të vegjël mori emrin e saj bazuar në parimin bazë që vlerësimet e parametrave të marra në bazë të saj duhet të plotësojnë: shuma e katrorëve të gabimit të modelit duhet të jetë minimale.
Shembuj të zgjidhjes së problemave me metodën e katrorëve më të vegjël
Shembulli 2.1. Ndërmarrja tregtare ka një rrjet të përbërë nga 12 dyqane, informacioni mbi aktivitetet e të cilave është paraqitur në tabelë. 2.1.
Menaxhmenti i kompanisë do të donte të dinte se si madhësia e vjetorit varet nga zona e shitjeve të dyqanit.
Tabela 2.1
|
Numri i dyqanit |
Qarkullimi vjetor, milion rubla |
Zone tregtare mije m 2 |
Zgjidhja e katrorëve më të vegjël. Le të caktojmë - qarkullimin vjetor të dyqanit -të, milion rubla; - siperfaqja e shitjes se dyqanit, mije m 2.

Fig.2.1. Scatterplot për shembullin 2.1
Të përcaktojë formën e marrëdhënies funksionale ndërmjet variablave dhe të ndërtojë një grafik shpërhapjeje (Fig. 2.1).
Bazuar në diagramin e shpërndarjes, mund të konkludojmë se qarkullimi vjetor është pozitivisht i varur nga zona e shitjes (d.m.th., y do të rritet me rritjen e ). Forma më e përshtatshme e lidhjes funksionale është − lineare.
Informacioni për llogaritjet e mëtejshme është paraqitur në Tabelën. 2.2. Duke përdorur metodën e katrorëve më të vegjël, ne vlerësojmë parametrat e modelit linear ekonometrik me një faktor

Tabela 2.2
Kështu,
Prandaj, me një rritje të zonës së tregtimit me 1 mijë m 2, duke qenë të barabarta gjërat e tjera, qarkullimi mesatar vjetor rritet me 67.8871 milion rubla.
Shembulli 2.2. Menaxhmenti i ndërmarrjes vuri re se qarkullimi vjetor varet jo vetëm nga zona e shitjes së dyqanit (shih shembullin 2.1), por edhe nga numri mesatar i vizitorëve. Informacioni përkatës është paraqitur në tabelë. 2.3.
Tabela 2.3
Zgjidhje. Shënoni - numrin mesatar të vizitorëve në dyqanin e th në ditë, mijëra njerëz.
Të përcaktojë formën e marrëdhënies funksionale ndërmjet variablave dhe të ndërtojë një grafik shpërhapjeje (Fig. 2.2).
Bazuar në diagramin e shpërndarjes, mund të konkludojmë se qarkullimi vjetor lidhet pozitivisht me numrin mesatar të vizitorëve në ditë (d.m.th., y do të rritet me rritjen e ). Forma e varësisë funksionale është lineare.

Oriz. 2.2. Scatterplot për shembull 2.2
Tabela 2.4
Në përgjithësi, është e nevojshme të përcaktohen parametrat e modelit ekonometrik me dy faktorë
y t \u003d a 0 + a 1 x 1 t + a 2 x 2 t + ε t
Informacioni i kërkuar për llogaritjet e mëtejshme është paraqitur në Tabelën. 2.4.
Le të vlerësojmë parametrat e një modeli ekonometrik linear me dy faktorë duke përdorur metodën e katrorëve më të vegjël.

Kështu,
Vlerësimi i koeficientit = 61.6583 tregon se, duke qenë të njëjtat gjëra të tjera, me një rritje të zonës së tregtimit me 1 mijë m 2, xhiroja vjetore do të rritet mesatarisht me 61.6583 milion rubla.
Funksionin e përafrojmë me një polinom të shkallës së 2-të. Për ta bërë këtë, ne llogarisim koeficientët e sistemit normal të ekuacioneve:
,  ,
, 
Le të hartojmë një sistem normal të katrorëve më të vegjël, i cili ka formën:

Zgjidhja e sistemit është e lehtë për t'u gjetur:, , .
Kështu, polinomi i shkallës së 2-të gjendet: .
Referenca teorike
Kthehu në faqe<Введение в вычислительную математику. Примеры>
Shembulli 2. Gjetja e shkallës optimale të një polinomi.
Kthehu në faqe<Введение в вычислительную математику. Примеры>
Shembulli 3. Nxjerrja e një sistemi normal ekuacionesh për gjetjen e parametrave të një varësie empirike.
Le të nxjerrim një sistem ekuacionesh për përcaktimin e koeficientëve dhe funksioneve ![]() , i cili kryen përafrimin rrënjë-mesatar-katror të funksionit të dhënë në lidhje me pikat. Hartoni një funksion
, i cili kryen përafrimin rrënjë-mesatar-katror të funksionit të dhënë në lidhje me pikat. Hartoni një funksion ![]() dhe shkruani kushtin e nevojshëm ekstrem për të:
dhe shkruani kushtin e nevojshëm ekstrem për të:

Atëherë sistemi normal do të marrë formën:

Ne kemi marrë një sistem linear ekuacionesh për parametra të panjohur dhe, i cili zgjidhet lehtësisht.
Referenca teorike
Kthehu në faqe<Введение в вычислительную математику. Примеры>
Shembull.
Të dhëna eksperimentale për vlerat e variablave X Dhe në janë dhënë në tabelë. 
Si rezultat i shtrirjes së tyre, funksioni ![]()
Duke përdorur metoda me katrorin më të vogël, përafroni këto të dhëna me një varësi lineare y=sëpatë+b(gjeni parametrat A Dhe b). Gjeni se cila nga dy rreshtat është më e mirë (në kuptimin e metodës së katrorëve më të vegjël) përafron të dhënat eksperimentale. Bëni një vizatim.
Thelbi i metodës së katrorëve më të vegjël (LSM).
Problemi është gjetja e koeficientëve linearë të varësisë për të cilat funksioni i dy ndryshoreve A Dhe b![]() merr vlerën më të vogël. Kjo është, duke pasur parasysh të dhënat A Dhe b shuma e devijimeve në katror të të dhënave eksperimentale nga drejtëza e gjetur do të jetë më e vogla. Kjo është e gjithë pika e metodës së katrorëve më të vegjël.
merr vlerën më të vogël. Kjo është, duke pasur parasysh të dhënat A Dhe b shuma e devijimeve në katror të të dhënave eksperimentale nga drejtëza e gjetur do të jetë më e vogla. Kjo është e gjithë pika e metodës së katrorëve më të vegjël.
Kështu, zgjidhja e shembullit reduktohet në gjetjen e ekstremit të një funksioni të dy ndryshoreve.
Nxjerrja e formulave për gjetjen e koeficientëve.
Përpilohet dhe zgjidhet një sistem me dy ekuacione me dy të panjohura. Gjetja e derivateve të pjesshme të funksioneve ![]() sipas variablave A Dhe b, ne i barazojmë këto derivate me zero.
sipas variablave A Dhe b, ne i barazojmë këto derivate me zero. 
Ne zgjidhim sistemin rezultues të ekuacioneve me çdo metodë (për shembull metoda e zëvendësimit ose metodën e Cramer-it) dhe merrni formulat për gjetjen e koeficientëve duke përdorur metodën e katrorëve më të vegjël (LSM). 
Me të dhëna A Dhe b funksionin ![]() merr vlerën më të vogël. Dëshmia e këtij fakti është dhënë më poshtë në tekstin në fund të faqes.
merr vlerën më të vogël. Dëshmia e këtij fakti është dhënë më poshtë në tekstin në fund të faqes.
Kjo është e gjithë metoda e katrorëve më të vegjël. Formula për gjetjen e parametrit a përmban shumat , , , dhe parametrin nështë sasia e të dhënave eksperimentale. Vlerat e këtyre shumave rekomandohet të llogariten veçmas.
Koeficient b gjetur pas llogaritjes a.
Është koha për të kujtuar shembullin origjinal.
Zgjidhje.
Në shembullin tonë n=5. Plotësojmë tabelën për lehtësinë e llogaritjes së shumave që përfshihen në formulat e koeficientëve të kërkuar. 
Vlerat në rreshtin e katërt të tabelës merren duke shumëzuar vlerat e rreshtit të dytë me vlerat e rreshtit të tretë për çdo numër i.
Vlerat në rreshtin e pestë të tabelës merren duke kuadruar vlerat e rreshtit të dytë për çdo numër i.
Vlerat e kolonës së fundit të tabelës janë shumat e vlerave nëpër rreshta.
Ne përdorim formulat e metodës së katrorëve më të vegjël për të gjetur koeficientët A Dhe b. Ne zëvendësojmë në to vlerat përkatëse nga kolona e fundit e tabelës: 
Prandaj, y=0,165x+2,184është drejtëza e dëshiruar e përafërt.
Mbetet për të gjetur se cila nga rreshtat y=0,165x+2,184 ose ![]() përafron më mirë të dhënat origjinale, pra për të bërë një vlerësim duke përdorur metodën e katrorëve më të vegjël.
përafron më mirë të dhënat origjinale, pra për të bërë një vlerësim duke përdorur metodën e katrorëve më të vegjël.
Vlerësimi i gabimit të metodës së katrorëve më të vegjël.
Për ta bërë këtë, duhet të llogaritni shumat e devijimeve në katror të të dhënave origjinale nga këto rreshta ![]() Dhe
Dhe ![]() , një vlerë më e vogël i korrespondon një rreshti që përafron më mirë të dhënat origjinale për sa i përket metodës së katrorëve më të vegjël.
, një vlerë më e vogël i korrespondon një rreshti që përafron më mirë të dhënat origjinale për sa i përket metodës së katrorëve më të vegjël. 
Që atëherë, linja y=0,165x+2,184 përafron më mirë të dhënat origjinale.
Ilustrim grafik i metodës së katrorëve më të vegjël (LSM).
Gjithçka duket e mrekullueshme në tabela. Vija e kuqe është vija e gjetur y=0,165x+2,184, vija blu është ![]() , pikat rozë janë të dhënat origjinale.
, pikat rozë janë të dhënat origjinale.

Për çfarë është, për çfarë janë të gjitha këto përafrime?
Unë personalisht përdor për të zgjidhur problemet e zbutjes së të dhënave, problemet e interpolimit dhe ekstrapolimit (në shembullin origjinal, mund t'ju kërkohet të gjeni vlerën e vlerës së vëzhguar y në x=3 ose kur x=6 sipas metodës MNC). Por ne do të flasim më shumë për këtë më vonë në një seksion tjetër të faqes.
Në krye të faqes
Dëshmi.
Kështu që kur të gjendet A Dhe b funksioni merr vlerën më të vogël, është e nevojshme që në këtë pikë matrica e formës kuadratike të diferencialit të rendit të dytë për funksionin. ![]() ishte pozitive definitive. Le ta tregojmë.
ishte pozitive definitive. Le ta tregojmë.
Diferenciali i rendit të dytë ka formën: 
Kjo eshte
Prandaj, matrica e formës kuadratike ka formën 
dhe vlerat e elementeve nuk varen nga A Dhe b.
Le të tregojmë se matrica është pozitive e përcaktuar. Kjo kërkon që këndi i të miturve të jetë pozitiv.
Minor këndor i rendit të parë  . Pabarazia është e rreptë, pasi pikat nuk përkojnë. Kjo do të nënkuptohet në atë që vijon.
. Pabarazia është e rreptë, pasi pikat nuk përkojnë. Kjo do të nënkuptohet në atë që vijon.
Minor këndor i rendit të dytë 
Le ta vërtetojmë këtë  metoda e induksionit matematik.
metoda e induksionit matematik.

konkluzioni: vlerat e gjetura A Dhe b korrespondojnë me vlerën më të vogël të funksionit ![]() , pra, janë parametrat e dëshiruar për metodën e katrorëve më të vegjël.
, pra, janë parametrat e dëshiruar për metodën e katrorëve më të vegjël.
E kuptoni ndonjëherë?
Porosit një zgjidhje
Në krye të faqes
Zhvillimi i një parashikimi duke përdorur metodën e katrorëve më të vegjël. Shembull i zgjidhjes së problemit
Ekstrapolimi - kjo është një metodë e kërkimit shkencor, e cila bazohet në shpërndarjen e tendencave, modeleve, marrëdhënieve të së kaluarës dhe të tashmes me zhvillimin e ardhshëm të objektit të parashikimit. Metodat e ekstrapolimit përfshijnë metoda e mesatares lëvizëse, metoda e zbutjes eksponenciale, metoda e katrorëve më të vegjël.
Thelbi Metoda e katrorëve më të vegjël konsiston në minimizimin e shumës së devijimeve katrore ndërmjet vlerave të vëzhguara dhe të llogaritura. Vlerat e llogaritura gjenden sipas ekuacionit të zgjedhur - ekuacionit të regresionit. Sa më e vogël të jetë distanca midis vlerave aktuale dhe atyre të llogaritura, aq më i saktë është parashikimi bazuar në ekuacionin e regresionit.
Analiza teorike e thelbit të fenomenit në studim, ndryshimi i të cilit shfaqet nga një seri kohore, shërben si bazë për zgjedhjen e një kurbë. Konsideratat rreth natyrës së rritjes së niveleve të serisë ndonjëherë merren parasysh. Pra, nëse rritja e prodhimit pritet në një progresion aritmetik, atëherë zbutja kryhet në vijë të drejtë. Nëse rezulton se rritja është eksponenciale, atëherë zbutja duhet të bëhet sipas funksionit eksponencial.
Formula e punës e metodës së katrorëve më të vegjël : Y t+1 = a*X + b, ku t + 1 është periudha e parashikimit; Уt+1 – tregues i parashikuar; a dhe b janë koeficientë; X është një simbol i kohës.
Koeficientët a dhe b llogariten sipas formulave të mëposhtme:
 |
 |
ku, Uf - vlerat aktuale të serisë së dinamikës; n është numri i niveleve në seritë kohore;
Zbutja e serive kohore me metodën e katrorëve më të vegjël shërben për të pasqyruar modelet e zhvillimit të fenomenit në studim. Në shprehjen analitike të një tendence, koha konsiderohet si një variabël i pavarur dhe nivelet e serisë veprojnë si funksion i kësaj ndryshoreje të pavarur.
Zhvillimi i një dukurie nuk varet nga sa vite kanë kaluar nga pika e fillimit, por nga faktorët që ndikuan në zhvillimin e tij, në çfarë drejtimi dhe me çfarë intensiteti. Nga kjo shihet qartë se zhvillimi i një dukurie në kohë shfaqet si rezultat i veprimit të këtyre faktorëve.
Vendosja e saktë e llojit të kurbës, llojit të varësisë analitike nga koha është një nga detyrat më të vështira të analizës parashikuese. .
Zgjedhja e llojit të funksionit që përshkruan trendin, parametrat e të cilit përcaktohen me metodën e katrorëve më të vegjël, në shumicën e rasteve është empirike, duke ndërtuar një sërë funksionesh dhe duke i krahasuar me njëri-tjetrin me vlerën e mesatares së rrënjës. - Gabim katror i llogaritur me formulën:
 |
ku Uf - vlerat aktuale të serisë së dinamikës; Ur - vlerat e llogaritura (të zbutura) të serive kohore; n është numri i niveleve në seritë kohore; p është numri i parametrave të përcaktuar në formulat që përshkruajnë trendin (tendenca e zhvillimit).
Disavantazhet e metodës së katrorëve më të vegjël :
- kur përpiqeni të përshkruani fenomenin ekonomik në studim duke përdorur një ekuacion matematikor, parashikimi do të jetë i saktë për një periudhë të shkurtër kohe dhe ekuacioni i regresionit duhet të rillogaritet kur informacioni i ri bëhet i disponueshëm;
- kompleksiteti i zgjedhjes së ekuacionit të regresionit, i cili është i zgjidhshëm duke përdorur programe standarde kompjuterike.
Një shembull i përdorimit të metodës së katrorëve më të vegjël për të zhvilluar një parashikim
Detyrë . Ka të dhëna që karakterizojnë nivelin e papunësisë në rajon, %
- Ndërtoni një parashikim të shkallës së papunësisë në rajon për muajt nëntor, dhjetor, janar, duke përdorur metodat: mesatare lëvizëse, zbutje eksponenciale, katrorët më të vegjël.
- Llogaritni gabimet në parashikimet që rezultojnë duke përdorur secilën metodë.
- Krahasoni rezultatet e marra, nxirrni përfundime.
Zgjidhja e katrorëve më të vegjël
Për zgjidhjen, ne do të përpilojmë një tabelë në të cilën do të bëjmë llogaritjet e nevojshme:
ε = 28,63/10 = 2,86% saktësia e parashikimit lartë.
konkluzioni : Krahasimi i rezultateve të marra në llogaritjet Metoda e mesatares lëvizëse , zbutje eksponenciale dhe metodën e katrorëve më të vegjël, mund të themi se gabimi mesatar relativ në llogaritjet me metodën e zbutjes eksponenciale bie brenda 20-50%. Kjo do të thotë se saktësia e parashikimit në këtë rast është vetëm e kënaqshme.
Në rastin e parë dhe të tretë, saktësia e parashikimit është e lartë, pasi gabimi mesatar relativ është më pak se 10%. Por metoda e mesatares lëvizëse bëri të mundur marrjen e rezultateve më të besueshme (parashikimi për nëntor - 1.52%, parashikimi për dhjetor - 1.53%, parashikimi për janar - 1.49%), pasi gabimi mesatar relativ kur përdorni këtë metodë është më i vogli - 1 ,13%.
Metoda me katrorin më të vogël
Artikuj të tjerë të lidhur:
Lista e burimeve të përdorura
- Rekomandime shkencore dhe metodologjike për çështjet e diagnostikimit të rreziqeve sociale dhe parashikimit të sfidave, kërcënimeve dhe pasojave sociale. Universiteti Shtetëror Social Rus. Moska. 2010;
- Vladimirova L.P. Parashikimi dhe planifikimi në kushtet e tregut: Proc. kompensim. M .: Shtëpia Botuese "Dashkov and Co", 2001;
- Novikova N.V., Pozdeeva O.G. Parashikimi i Ekonomisë Kombëtare: Udhëzues Edukativo-Metodologjik. Yekaterinburg: Shtëpia Botuese Ural. shteti ekonomisë universiteti, 2007;
- Slutskin L.N. Kurs MBA në parashikimin e biznesit. Moskë: Librat e Biznesit Alpina, 2006.
Programi MNE
Futni të dhëna
Të dhënat dhe përafrimi y = a + b x
i- numri i pikës eksperimentale;
x i- vlera e parametrit fiks në pikë i;
y i- vlera e parametrit të matur në pikë i;
ω i- matja e peshës në pikë i;
y i, llogarit.- diferenca ndërmjet vlerës së matur dhe vlerës së llogaritur nga regresioni y në pikën i;
S x i (x i)- vlerësimi i gabimit x i gjatë matjes y në pikën i.
Të dhënat dhe përafrimi y = k x
| i | x i | y i | ω i | y i, llogarit. | Δy i | S x i (x i) |
|---|
Klikoni në grafik
Manuali i përdorimit për programin online MNC.
Në fushën e të dhënave, vendosni në secilën rresht të veçantë vlerat e 'x' dhe 'y' në një pikë eksperimentale. Vlerat duhet të ndahen me hapësirë të bardhë (hapësirë ose skedë).
Vlera e tretë mund të jetë pesha e pikës së `w`. Nëse pesha e pikës nuk është e specifikuar, atëherë ajo është e barabartë me një. Në shumicën dërrmuese të rasteve, peshat e pikave eksperimentale janë të panjohura ose të pallogaritura; të gjitha të dhënat eksperimentale konsiderohen ekuivalente. Ndonjëherë peshat në gamën e studiuar të vlerave nuk janë definitivisht ekuivalente dhe madje mund të llogariten teorikisht. Për shembull, në spektrofotometri, peshat mund të llogariten duke përdorur formula të thjeshta, megjithëse në thelb të gjithë e neglizhojnë këtë për të ulur kostot e punës.
Të dhënat mund të ngjiten përmes kujtesës së fragmenteve nga një fletëllogaritëse e paketës së zyrës, si p.sh. Excel nga Microsoft Office ose Calc nga Open Office. Për ta bërë këtë, në spreadsheet, zgjidhni gamën e të dhënave për të kopjuar, kopjoni në kujtesën e fragmenteve dhe ngjitni të dhënat në fushën e të dhënave në këtë faqe.
Për të llogaritur me metodën e katrorëve më të vegjël, kërkohen të paktën dy pika për të përcaktuar dy koeficientët "b" - tangjenten e këndit të pjerrësisë së drejtëzës dhe "a" - vlera e prerë nga vija e drejtë në "y". boshti `.
Për të vlerësuar gabimin e koeficientëve të llogaritur të regresionit, është e nevojshme të vendosni numrin e pikave eksperimentale në më shumë se dy.
Metoda e katrorëve më të vegjël (LSM).
Sa më i madh të jetë numri i pikëve eksperimentale, aq më i saktë është vlerësimi statistikor i koeficientëve (për shkak të uljes së koeficientit të Studentit) dhe aq më i afërt është vlerësimi me vlerësimin e kampionit të përgjithshëm.
Marrja e vlerave në çdo pikë eksperimentale shpesh shoqërohet me kosto të konsiderueshme të punës, prandaj, shpesh kryhet një numër kompromisi i eksperimenteve, i cili jep një vlerësim të tretshëm dhe nuk çon në kosto të tepërta të punës. Si rregull, numri i pikave eksperimentale për një varësi lineare të katrorëve më të vegjël me dy koeficientë zgjidhet në rajonin 5-7 pikë.
Një teori e shkurtër e katrorëve më të vegjël për varësinë lineare
Supozoni se kemi një grup të dhënash eksperimentale në formën e çifteve të vlerave [`y_i`, `x_i`], ku `i` është numri i një matjeje eksperimentale nga 1 në `n`; `y_i` - vlera e vlerës së matur në pikën `i`; `x_i` - vlera e parametrit që vendosëm në pikën `i`.
Një shembull është funksionimi i ligjit të Ohm-it. Duke ndryshuar tensionin (diferencën e mundshme) midis seksioneve të qarkut elektrik, ne matim sasinë e rrymës që kalon nëpër këtë seksion. Fizika na jep varësinë e gjetur eksperimentalisht:
`I=U/R`,
ku `I` - forca aktuale; `R` - rezistencë; `U` - tension.
Në këtë rast, `y_i` është vlera aktuale e matur, dhe `x_i` është vlera e tensionit.
Si shembull tjetër, merrni parasysh thithjen e dritës nga një tretësirë e një lënde në tretësirë. Kimia na jep formulën:
`A = εl C`,
ku `A` është dendësia optike e tretësirës; `ε` - transmetimi i tretësirës; `l` - gjatësia e rrugës kur drita kalon nëpër një kuvetë me një zgjidhje; 'C' është përqendrimi i substancës së tretur.
Në këtë rast, `y_i` është densiteti optik i matur `A`, dhe `x_i` është përqendrimi i substancës që kemi vendosur.
Do të shqyrtojmë rastin kur gabimi relativ në vendosjen e `x_i` është shumë më i vogël se gabimi relativ në matjen e `y_i`. Ne gjithashtu do të supozojmë se të gjitha vlerat e matura të `y_i` janë të rastësishme dhe të shpërndara normalisht, d.m.th. respektoni ligjin e shpërndarjes normale.
Në rastin e një varësie lineare të `y` nga `x`, mund të shkruajmë varësinë teorike:
`y = a + bx`.
Nga pikëpamja gjeometrike, koeficienti "b" tregon tangjenten e këndit të prirjes së drejtëzës në boshtin "x", dhe koeficienti "a" - vlerën e "y" në pikën e kryqëzimit të vijë me boshtin `y` (për `x = 0`).
Gjetja e parametrave të vijës së regresionit.
Në një eksperiment, vlerat e matura të `y_i` nuk mund të qëndrojnë saktësisht në vijën teorike për shkak të gabimeve të matjes, të cilat janë gjithmonë të natyrshme në jetën reale. Prandaj, një ekuacion linear duhet të përfaqësohet nga një sistem ekuacionesh:
`y_i = a + b x_i + ε_i` (1),
ku `ε_i` është gabimi i panjohur i matjes i `y` në eksperimentin e `i`.
Varësia (1) quhet gjithashtu regresioni, d.m.th. varësia e dy sasive nga njëra-tjetra me rëndësi statistikore.
Detyra e rivendosjes së varësisë është gjetja e koeficientëve `a` dhe `b` nga pikat eksperimentale [`y_i`, `x_i`].
Për të gjetur koeficientët zakonisht përdoret "a" dhe "b". metoda më e vogël e katrorit(MNK). Është një rast i veçantë i parimit të gjasave maksimale.
Le ta rishkruajmë (1) si `ε_i = y_i - a - b x_i`.
Atëherë shuma e gabimeve në katror do të jetë
`Φ = shuma_(i=1)^(n) ε_i^2 = shuma_(i=1)^(n) (y_i - a - b x_i)^2`. (2)
Parimi i metodës së katrorëve më të vegjël është të minimizohet shuma (2) në lidhje me parametrat "a" dhe "b"..
Minimumi arrihet kur derivatet e pjesshëm të shumës (2) në lidhje me koeficientët "a" dhe "b" janë të barabarta me zero:
`frac(i pjesshëm Φ)(i pjesshëm a) = frac(shuma e pjesshme_(i=1)^(n) (y_i - a - b x_i)^2)(i pjesshëm a) = 0`
`frac(i pjesshëm Φ)(i pjesshëm b) = frac(shuma e pjesshme_(i=1)^(n) (y_i - a - b x_i)^2)(i pjesshëm b) = 0`
Duke zgjeruar derivatet, marrim një sistem prej dy ekuacionesh me dy të panjohura:
`shuma_(i=1)^(n) (2a + 2bx_i - 2y_i) = shuma_(i=1)^(n) (a + bx_i - y_i) = 0`
`sum_(i=1)^(n) (2bx_i^2 + 2ax_i - 2x_iy_i) = shuma_(i=1)^(n) (bx_i^2 + ax_i - x_iy_i) = 0`
Ne hapim kllapat dhe transferojmë shumat e pavarura nga koeficientët e dëshiruar në gjysmën tjetër, marrim një sistem ekuacionesh lineare:
`shuma_(i=1)^(n) y_i = a n + b shuma_(i=1)^(n) bx_i`
`sum_(i=1)^(n) x_iy_i = një shumë_(i=1)^(n) x_i + b shuma_(i=1)^(n) x_i^2`
Duke zgjidhur sistemin që rezulton, gjejmë formula për koeficientët "a" dhe "b":
`a = frac(sum_(i=1)^(n) y_i shuma_(i=1)^(n) x_i^2 - shuma_(i=1)^(n) x_i shuma_(i=1)^(n ) x_iy_i) (n shuma_(i=1)^(n) x_i^2 — (shuma_(i=1)^(n) x_i)^2)` (3.1)
`b = frac(n shuma_(i=1)^(n) x_iy_i - shuma_(i=1)^(n) x_i shuma_(i=1)^(n) y_i) (n shuma_(i=1)^ (n) x_i^2 - (shuma_(i=1)^(n) x_i)^2)` (3.2)
Këto formula kanë zgjidhje kur `n > 1` (vija mund të vizatohet duke përdorur të paktën 2 pika) dhe kur përcaktorja `D = n shuma_(i=1)^(n) x_i^2 — (shuma_(i= 1 )^(n) x_i)^2 != 0`, d.m.th. kur pikat `x_i` në eksperiment janë të ndryshme (d.m.th. kur vija nuk është vertikale).
Vlerësimi i gabimeve në koeficientët e vijës së regresionit
Për një vlerësim më të saktë të gabimit në llogaritjen e koeficientëve "a" dhe "b", është i dëshirueshëm një numër i madh pikash eksperimentale. Kur `n = 2`, është e pamundur të vlerësohet gabimi i koeficientëve, sepse vija e përafërt do të kalojë në mënyrë unike nëpër dy pika.
Përcaktohet gabimi i ndryshores së rastësishme `V` ligji i akumulimit të gabimeve
`S_V^2 = shuma_(i=1)^p (frac(i pjesshëm f)(i pjesshëm z_i))^2 S_(z_i)^2`,
ku `p` është numri i parametrave `z_i` me gabim `S_(z_i)` që ndikojnë në gabimin `S_V`;
`f` është një funksion varësie e `V` në `z_i`.
Le të shkruajmë ligjin e akumulimit të gabimeve për gabimin e koeficientëve `a` dhe `b`
`S_a^2 = shuma_(i=1)^(n)(frac(i pjesshëm a)(i pjesshëm y_i))^2 S_(y_i)^2 + shuma_(i=1)^(n)(frac(i pjesshëm a )(x_i i pjesshëm))^2 S_(x_i)^2 = S_y^2 shuma_(i=1)^(n)(frac(i pjesshëm a)(i pjesshëm y_i))^2 `,
`S_b^2 = shuma_(i=1)^(n)(frac(i pjesshëm b)(i pjesshëm y_i))^2 S_(y_i)^2 + shuma_(i=1)^(n)(frac(i pjesshëm b )(x_i i pjesshëm))^2 S_(x_i)^2 = S_y^2 shuma_(i=1)^(n)(frac(i pjesshëm b)(i pjesshëm y_i))^2 `,
sepse `S_(x_i)^2 = 0` (më parë kemi bërë një rezervë se gabimi i `x` është i papërfillshëm).
`S_y^2 = S_(y_i)^2` - gabimi (varianca, devijimi standard në katror) në dimensionin `y`, duke supozuar se gabimi është uniform për të gjitha vlerat `y`.
Duke zëvendësuar formulat për llogaritjen e "a" dhe "b" në shprehjet që rezultojnë, marrim
`S_a^2 = S_y^2 frac(shuma_(i=1)^(n) (shuma_(i=1)^(n) x_i^2 - x_i shuma_(i=1)^(n) x_i)^2 ) (D^2) = S_y^2 frac((n shuma_(i=1)^(n) x_i^2 - (shuma_(i=1)^(n) x_i)^2) shuma_(i=1) ^(n) x_i^2) (D^2) = S_y^2 frac(shuma_(i=1)^(n) x_i^2) (D)` (4.1)
`S_b^2 = S_y^2 frac(shuma_(i=1)^(n) (n x_i - shuma_(i=1)^(n) x_i)^2) (D^2) = S_y^2 frac( n (n shuma_(i=1)^(n) x_i^2 - (shuma_(i=1)^(n) x_i)^2)) (D^2) = S_y^2 frac(n) (D) ` (4.2)
Në shumicën e eksperimenteve reale, vlera e 'Sy' nuk matet. Për ta bërë këtë, është e nevojshme të kryhen disa matje (eksperimente) paralele në një ose disa pika të planit, gjë që rrit kohën (dhe ndoshta koston) e eksperimentit. Prandaj, zakonisht supozohet se devijimi i `y` nga vija e regresionit mund të konsiderohet i rastësishëm. Vlerësimi i variancës `y` në këtë rast llogaritet me formulën.
`S_y^2 = S_(y, pushim)^2 = frac(shuma_(i=1)^n (y_i - a - b x_i)^2) (n-2)`.
Pjesëtuesi `n-2` shfaqet sepse kemi reduktuar numrin e shkallëve të lirisë për shkak të llogaritjes së dy koeficientëve për të njëjtin mostër të të dhënave eksperimentale.
Ky vlerësim quhet gjithashtu varianca e mbetur në lidhje me vijën e regresionit `S_(y, pushim)^2`.
Vlerësimi i rëndësisë së koeficientëve kryhet sipas kriterit të Studentit
`t_a = frac(|a|) (S_a)`, `t_b = frac(|b|) (S_b)`
Nëse kriteret e llogaritura `t_a`, `t_b` janë më të vogla se kriteret e tabelës `t(P, n-2)`, atëherë konsiderohet se koeficienti përkatës nuk është dukshëm i ndryshëm nga zero me një probabilitet të caktuar `P`.
Për të vlerësuar cilësinë e përshkrimit të një marrëdhënieje lineare, mund të krahasoni `S_(y, pushim)^2` dhe `S_(bar y)` në lidhje me mesataren duke përdorur kriterin Fisher.
`S_(bar y) = frac(shuma_(i=1)^n (y_i - bar y)^2) (n-1) = frac(shuma_(i=1)^n (y_i - (shuma_(i= 1)^n y_i) /n)^2) (n-1)` - vlerësim mostër e variancës së `y` në lidhje me mesataren.
Për të vlerësuar efektivitetin e ekuacionit të regresionit për përshkrimin e varësisë, llogaritet koeficienti Fisher
`F = S_(shirit y) / S_(y, pushim)^2`,
i cili krahasohet me koeficientin tabelor Fisher `F(p, n-1, n-2)`.
Nëse `F > F(P, n-1, n-2)`, ndryshimi midis përshkrimit të varësisë `y = f(x)` duke përdorur ekuacionin e regresionit dhe përshkrimit duke përdorur mesataren konsiderohet statistikisht i rëndësishëm me probabilitet `P`. Ato. regresioni përshkruan më mirë varësinë sesa përhapjen e `y` rreth mesatares.
Klikoni në grafik
për të shtuar vlera në tabelë
Metoda me katrorin më të vogël. Metoda e katrorëve më të vegjël nënkupton përcaktimin e parametrave të panjohur a, b, c, varësinë funksionale të pranuar
Metoda e katrorëve më të vegjël nënkupton përcaktimin e parametrave të panjohur a, b, c,… varësia funksionale e pranuar
y = f(x,a,b,c,…),
e cila do të siguronte një minimum të katrorit mesatar (variancës) të gabimit
 , (24)
, (24)
ku x i , y i - grup çiftesh numrash të përftuar nga eksperimenti.
Meqenëse kushti për ekstremin e një funksioni të disa ndryshoreve është kushti që derivatet e tij të pjesshëm të jenë të barabartë me zero, atëherë parametrat a, b, c,… përcaktohen nga sistemi i ekuacioneve:
; ; ; … (25)
Duhet mbajtur mend se metoda e katrorëve më të vegjël përdoret për të zgjedhur parametrat pas formës së funksionit y = f(x) të përcaktuara.
Nëse nga konsideratat teorike është e pamundur të nxirren ndonjë përfundim se cila duhet të jetë formula empirike, atëherë duhet të udhëhiqet nga paraqitjet vizuale, kryesisht një paraqitje grafike e të dhënave të vëzhguara.
Në praktikë, më së shpeshti kufizohet në llojet e mëposhtme të funksioneve:
1) lineare ![]() ;
;
2) kuadratik a .
Zgjedhja e llojit të funksionit të regresionit, d.m.th. lloji i modelit të konsideruar të varësisë së Y nga X (ose X në Y), për shembull, një model linear y x = a + bx, është e nevojshme të përcaktohen vlerat specifike të koeficientëve të modelit.
Për vlera të ndryshme të a dhe b, është e mundur të ndërtojmë një numër të pafund varësish të formës y x =a+bx, d.m.th., ka një numër të pafund rreshtash në planin koordinativ, por ne kemi nevojë për një varësi të tillë që korrespondon me vlerat e vëzhguara në mënyrën më të mirë. Kështu, problemi reduktohet në zgjedhjen e koeficientëve më të mirë.
Ne jemi duke kërkuar për një funksion linear a + bx, bazuar vetëm në një numër të caktuar vëzhgimesh të disponueshme. Për të gjetur funksionin me përshtatjen më të mirë me vlerat e vëzhguara, ne përdorim metodën e katrorëve më të vegjël.
Shënoni: Y i - vlera e llogaritur me ekuacionin Y i =a+bx i . y i - vlera e matur, ε i =y i -Y i - diferenca ndërmjet vlerave të matura dhe të llogaritura, ε i =y i -a-bx i .
Metoda e katrorëve më të vegjël kërkon që ε i, diferenca midis y i matur dhe vlerave të Y i të llogaritura nga ekuacioni, të jetë minimale. Prandaj, ne gjejmë koeficientët a dhe b në mënyrë që shuma e devijimeve në katror të vlerave të vëzhguara nga vlerat në vijën e drejtë të regresionit të jetë më e vogla:
Duke studiuar këtë funksion të argumenteve a dhe me ndihmën e derivateve të një ekstremi, mund të vërtetojmë se funksioni merr një vlerë minimale nëse koeficientët a dhe b janë zgjidhje të sistemit:
 (2)
(2)
Nëse i ndajmë të dyja anët e ekuacioneve normale me n, marrim:

Duke pasur parasysh se  (3)
(3)
Marr  , nga këtu, duke zëvendësuar vlerën e a në ekuacionin e parë, marrim:
, nga këtu, duke zëvendësuar vlerën e a në ekuacionin e parë, marrim:

Në këtë rast, b quhet koeficienti i regresionit; a quhet anëtar i lirë i ekuacionit të regresionit dhe llogaritet me formulën:
Vija e drejtë që rezulton është një vlerësim për vijën e regresionit teorik. Ne kemi:
Kështu që, ![]() është një ekuacion i regresionit linear.
është një ekuacion i regresionit linear.
Regresioni mund të jetë i drejtpërdrejtë (b>0) dhe i anasjelltë (b Shembulli 1. Rezultatet e matjes së vlerave X dhe Y janë dhënë në tabelë:
| x i | -2 | 0 | 1 | 2 | 4 |
| y i | 0.5 | 1 | 1.5 | 2 | 3 |
Duke supozuar se ekziston një lidhje lineare midis X dhe Y y=a+bx, caktoni koeficientët a dhe b duke përdorur metodën e katrorëve më të vegjël.
Zgjidhje. Këtu n=5
x i =-2+0+1+2+4=5;
x i 2 =4+0+1+4+16=25
x i y i =-2 0,5+0 1+1 1,5+2 2+4 3=16,5
y i =0,5+1+1,5+2+3=8
dhe sistemi normal (2) ka formën ![]()
Duke zgjidhur këtë sistem, marrim: b=0.425, a=1.175. Prandaj y=1,175+0,425x.
Shembulli 2. Ekziston një mostër prej 10 vëzhgimesh të treguesve ekonomikë (X) dhe (Y).
| x i | 180 | 172 | 173 | 169 | 175 | 170 | 179 | 170 | 167 | 174 |
| y i | 186 | 180 | 176 | 171 | 182 | 166 | 182 | 172 | 169 | 177 |
Kërkohet të gjendet një ekuacion i regresionit të mostrës Y në X. Ndërtoni një linjë regresioni mostër Y në X.
Zgjidhje. 1. Le t'i renditim të dhënat sipas vlerave x i dhe y i. Ne marrim një tabelë të re:
| x i | 167 | 169 | 170 | 170 | 172 | 173 | 174 | 175 | 179 | 180 |
| y i | 169 | 171 | 166 | 172 | 180 | 176 | 177 | 182 | 182 | 186 |
Për të thjeshtuar llogaritjet, do të përpilojmë një tabelë llogaritëse në të cilën do të vendosim vlerat e nevojshme numerike.
| x i | y i | x i 2 | x i y i |
| 167 | 169 | 27889 | 28223 |
| 169 | 171 | 28561 | 28899 |
| 170 | 166 | 28900 | 28220 |
| 170 | 172 | 28900 | 29240 |
| 172 | 180 | 29584 | 30960 |
| 173 | 176 | 29929 | 30448 |
| 174 | 177 | 30276 | 30798 |
| 175 | 182 | 30625 | 31850 |
| 179 | 182 | 32041 | 32578 |
| 180 | 186 | 32400 | 33480 |
| ∑x i =1729 | ∑y i =1761 | ∑x i 2 299105 | ∑x i y i =304696 |
| x=172.9 | y=176.1 | x i 2 =29910.5 | xy=30469.6 |
Sipas formulës (4), ne llogarisim koeficientin e regresionit
dhe sipas formulës (5)
Kështu, ekuacioni i regresionit të mostrës duket si y=-59.34+1.3804x.
Le të vizatojmë pikat (x i ; y i) në planin koordinativ dhe të shënojmë vijën e regresionit.

Fig 4
Figura 4 tregon se si janë vendosur vlerat e vëzhguara në lidhje me vijën e regresionit. Për të vlerësuar numerikisht devijimet e y i nga Y i, ku y i janë vlerat e vëzhguara dhe Y i janë vlerat e përcaktuara me regresion, ne do të bëjmë një tabelë:
| x i | y i | Y i | Y i -y i |
| 167 | 169 | 168.055 | -0.945 |
| 169 | 171 | 170.778 | -0.222 |
| 170 | 166 | 172.140 | 6.140 |
| 170 | 172 | 172.140 | 0.140 |
| 172 | 180 | 174.863 | -5.137 |
| 173 | 176 | 176.225 | 0.225 |
| 174 | 177 | 177.587 | 0.587 |
| 175 | 182 | 178.949 | -3.051 |
| 179 | 182 | 184.395 | 2.395 |
| 180 | 186 | 185.757 | -0.243 |
Vlerat e Y i llogariten sipas ekuacionit të regresionit.
Devijimi i dukshëm i disa vlerave të vëzhguara nga vija e regresionit shpjegohet me numrin e vogël të vëzhgimeve. Gjatë studimit të shkallës së varësisë lineare të Y nga X, merret parasysh numri i vëzhgimeve. Forca e varësisë përcaktohet nga vlera e koeficientit të korrelacionit.
Metoda me katrorin më të vogël përdoret për të vlerësuar parametrat e ekuacionit të regresionit.Një nga metodat për studimin e marrëdhënieve stokastike midis veçorive është analiza e regresionit.
Analiza e regresionit është nxjerrja e një ekuacioni regresioni, i cili përdoret për të gjetur vlerën mesatare të një ndryshoreje të rastësishme (veçori-rezultat), nëse dihet vlera e një ndryshoreje tjetër (ose të tjera) (faktorë-faktorë). Ai përfshin hapat e mëposhtëm:
- zgjedhja e formës së lidhjes (lloji i ekuacionit të regresionit analitik);
- vlerësimi i parametrave të ekuacionit;
- vlerësimi i cilësisë së ekuacionit të regresionit analitik.
Në rastin e marrëdhënies së çiftit linear, ekuacioni i regresionit do të marrë formën: y i =a+b·x i +u i . Parametrat e këtij ekuacioni a dhe b janë vlerësuar nga të dhënat e vëzhgimit statistikor x dhe y. Rezultati i një vlerësimi të tillë është ekuacioni: , ku , - vlerësimet e parametrave a dhe b , - vlera e veçorisë efektive (ndryshores) e përftuar nga ekuacioni i regresionit (vlera e llogaritur).
Më e përdorura për vlerësimin e parametrave është metoda e katrorëve më të vogël (LSM).
Metoda e katrorëve më të vegjël jep vlerësimet më të mira (të qëndrueshme, efikase dhe të paanshme) të parametrave të ekuacionit të regresionit. Por vetëm nëse plotësohen supozime të caktuara në lidhje me termin e rastësishëm (u) dhe variablin e pavarur (x) (shih supozimet OLS).
Problemi i vlerësimit të parametrave të një ekuacioni të çiftit linear me metodën e katrorëve më të vegjël konsiston në sa vijon: për të marrë vlerësime të tilla të parametrave, në të cilat shuma e devijimeve në katror të vlerave aktuale të veçorisë efektive - y i nga vlerat e llogaritura - është minimale.
Formalisht Kriteri OLS mund të shkruhet kështu:  .
.
Klasifikimi i metodave të katrorëve më të vegjël
- Metoda me katrorin më të vogël.
- Metoda e gjasave maksimale (për një model normal klasik të regresionit linear, është postuluar normaliteti i mbetjeve të regresionit).
- Metoda e përgjithësuar e katrorëve më të vegjël të GLSM përdoret në rastin e autokorrelacionit të gabimit dhe në rastin e heteroskedasticitetit.
- Metoda e katrorëve më të vegjël të ponderuar (një rast i veçantë i GLSM me mbetje heteroskedastike).
Ilustroni thelbin metoda klasike e katrorëve më të vegjël grafikisht. Për ta bërë këtë, ne do të ndërtojmë një grafik me pika sipas të dhënave të vëzhgimit (x i, y i, i=1;n) në një sistem koordinativ drejtkëndor (një grafik i tillë pikash quhet fushë korrelacioni). Le të përpiqemi të gjejmë një vijë të drejtë që është më afër pikave të fushës së korrelacionit. Sipas metodës së katrorëve më të vegjël, vija zgjidhet në mënyrë që shuma e distancave vertikale në katror ndërmjet pikave të fushës së korrelacionit dhe kësaj drejtëze të jetë minimale. 
Shënimi matematik i këtij problemi:  .
.
Vlerat e y i dhe x i =1...n janë të njohura për ne, këto janë të dhëna vëzhgimi. Në funksionin S ato janë konstante. Variablat në këtë funksion janë vlerësimet e kërkuara të parametrave - , . Për të gjetur minimumin e një funksioni prej 2 ndryshoresh, është e nevojshme të llogariten derivatet e pjesshme të këtij funksioni në lidhje me secilin prej parametrave dhe t'i barazojmë me zero, d.m.th.  .
.
Si rezultat, marrim një sistem prej 2 ekuacionesh normale lineare: 
Duke zgjidhur këtë sistem, gjejmë vlerësimet e kërkuara të parametrave: 
Korrektësia e llogaritjes së parametrave të ekuacionit të regresionit mund të kontrollohet duke krahasuar shumat (disa mospërputhje është e mundur për shkak të rrumbullakimit të llogaritjeve).
Për të llogaritur vlerësimet e parametrave, mund të ndërtoni Tabelën 1.
Shenja e koeficientit të regresionit b tregon drejtimin e marrëdhënies (nëse b > 0, marrëdhënia është e drejtpërdrejtë, nëse b<0, то связь обратная). Величина b показывает на сколько единиц изменится в среднем признак-результат -y при изменении признака-фактора - х на 1 единицу своего измерения.
Formalisht, vlera e parametrit a është vlera mesatare e y për x e barabartë me zero. Nëse faktori i shenjës nuk ka dhe nuk mund të ketë një vlerë zero, atëherë interpretimi i mësipërm i parametrit a nuk ka kuptim.
Vlerësimi i ngushtësisë së marrëdhënies ndërmjet veçorive
kryhet duke përdorur koeficientin e korrelacionit të çiftit linear - r x,y . Mund të llogaritet duke përdorur formulën:  . Për më tepër, koeficienti i korrelacionit të çiftit linear mund të përcaktohet në terma të koeficientit të regresionit b:
. Për më tepër, koeficienti i korrelacionit të çiftit linear mund të përcaktohet në terma të koeficientit të regresionit b:  .
.
Gama e vlerave të pranueshme të koeficientit linear të korrelacionit të çiftit është nga -1 në +1. Shenja e koeficientit të korrelacionit tregon drejtimin e marrëdhënies. Nëse r x, y >0, atëherë lidhja është e drejtpërdrejtë; nëse r x, y<0, то связь обратная.
Nëse ky koeficient është afër unitetit në modul, atëherë marrëdhënia midis veçorive mund të interpretohet si një lidhje lineare mjaft e ngushtë. Nëse moduli i tij është i barabartë me një ê r x, y ê =1, atëherë lidhja ndërmjet veçorive është funksionale lineare. Nëse tiparet x dhe y janë linearisht të pavarura, atëherë r x,y është afër 0.
Tabela 1 mund të përdoret gjithashtu për të llogaritur r x,y.
Për të vlerësuar cilësinë e ekuacionit të regresionit të marrë, llogaritet koeficienti teorik i përcaktimit - R 2 yx:  ,
,
ku d 2 është varianca y e shpjeguar nga ekuacioni i regresionit;
e 2 - varianca e mbetur (e pashpjegueshme nga ekuacioni i regresionit) y ;
s 2 y - varianca totale (totali) y .
Koeficienti i përcaktimit karakterizon pjesën e variacionit (dispersionit) të veçorisë që rezulton y, e shpjeguar me regresion (dhe, rrjedhimisht, faktorin x), në variacionin total (dispersionin) y. Koeficienti i përcaktimit R 2 yx merr vlera nga 0 në 1. Prandaj, vlera 1-R 2 yx karakterizon proporcionin e variancës y të shkaktuar nga ndikimi i faktorëve të tjerë që nuk merren parasysh në model dhe gabimet e specifikimit.
Me regresion linear të çiftëzuar R 2 yx =r 2 yx .
Metoda me katrorin më të vogël
Metoda me katrorin më të vogël ( MNK, OLS, Sheshet më të vogla të zakonshme) - një nga metodat bazë të analizës së regresionit për vlerësimin e parametrave të panjohur të modeleve të regresionit nga të dhënat e mostrës. Metoda bazohet në minimizimin e shumës së katrorëve të mbetjeve të regresionit.
Duhet të theksohet se vetë metoda e katrorëve më të vegjël mund të quhet metodë për zgjidhjen e një problemi në çdo fushë, nëse zgjidhja përbëhet ose plotëson një kriter të caktuar për minimizimin e shumës së katrorëve të disa funksioneve të ndryshoreve të panjohura. Prandaj, metoda e katrorëve më të vegjël mund të përdoret gjithashtu për një paraqitje të përafërt (përafrim) të një funksioni të caktuar me funksione të tjera (më të thjeshta), kur gjendet një grup sasish që plotësojnë ekuacionet ose kufizimet, numri i të cilave e kalon numrin e këtyre sasive. , etj.
Thelbi i MNC
Lëreni një model (parametrik) të varësisë probabilistike (regresioni) midis ndryshores (e shpjeguar) y dhe shumë faktorë (variabla shpjegues) x
ku është vektori i parametrave të modelit të panjohur
- Gabim i rastësishëm i modelit.Le të ketë gjithashtu vëzhgime të mostrave të vlerave të variablave të treguar. Le të jetë numri i vëzhgimit (). Pastaj janë vlerat e variablave në vëzhgimin e -të. Pastaj, për vlerat e dhëna të parametrave b, është e mundur të llogariten vlerat teorike (modele) të ndryshores së shpjeguar y:
Vlera e mbetjeve varet nga vlerat e parametrave b.
Thelbi i LSM (i zakonshëm, klasik) është gjetja e parametrave të tillë b për të cilët shuma e katrorëve të mbetjeve (eng. Shuma e mbetur e katrorëve) do të jetë minimale:
Në rastin e përgjithshëm, ky problem mund të zgjidhet me metoda numerike të optimizimit (minimizimit). Në këtë rast, flitet për katrorët më të vegjël jolinearë(NLS ose NLLS - Anglisht. Katrore më të vogla jo lineare). Në shumë raste, mund të merret një zgjidhje analitike. Për të zgjidhur problemin e minimizimit, është e nevojshme të gjenden pikat stacionare të funksionit duke e diferencuar atë në lidhje me parametrat e panjohur b, duke barazuar derivatet me zero dhe duke zgjidhur sistemin e ekuacioneve që rezulton:
Nëse gabimet e rastësishme të modelit shpërndahen normalisht, kanë të njëjtën variancë dhe nuk janë të ndërlidhura me njëri-tjetrin, vlerësimet e parametrave të katrorëve më të vegjël janë të njëjta me vlerësimet e metodës së gjasave maksimale (MLM).
LSM në rastin e një modeli linear
Le të jetë lineare varësia e regresionit:
Le y- vektori i kolonës së vëzhgimeve të ndryshores së shpjeguar, dhe - matrica e vëzhgimeve të faktorëve (rreshtat e matricës - vektorët e vlerave të faktorëve në një vëzhgim të caktuar, sipas kolonave - vektori i vlerave të një faktori të caktuar në të gjitha vëzhgimet) . Paraqitja matricore e modelit linear ka formën:
Atëherë vektori i vlerësimeve të variablit të shpjeguar dhe vektori i mbetjeve të regresionit do të jetë i barabartë me
në përputhje me rrethanat, shuma e katrorëve të mbetjeve të regresionit do të jetë e barabartë me
Duke e diferencuar këtë funksion në lidhje me vektorin e parametrave dhe duke barazuar derivatet me zero, marrim një sistem ekuacionesh (në formë matrice):
.Zgjidhja e këtij sistemi ekuacionesh jep formulën e përgjithshme për vlerësimet e katrorëve më të vegjël për modelin linear:
Për qëllime analitike, paraqitja e fundit e kësaj formule rezulton të jetë e dobishme. Nëse të dhënat në modelin e regresionit të përqendruar, atëherë në këtë paraqitje matrica e parë ka kuptimin e matricës së mostrës së kovariancës së faktorëve, dhe e dyta është vektori i kovariancave të faktorëve me variabël të varur. Nëse, përveç kësaj, të dhënat janë gjithashtu normalizuar në SKO (d.m.th., në fund të fundit të standardizuara), atëherë matrica e parë ka kuptimin e matricës së korrelacionit të mostrës së faktorëve, vektori i dytë - vektori i korrelacioneve të mostrës së faktorëve me variablin e varur.
Një veti e rëndësishme e vlerësimeve LLS për modelet me një konstante- vija e regresionit të ndërtuar kalon nëpër qendrën e gravitetit të të dhënave të mostrës, domethënë përmbushet barazia:
Në veçanti, në rastin ekstrem, kur i vetmi regresor është një konstante, gjejmë se vlerësimi OLS i një parametri të vetëm (vetë konstanta) është i barabartë me vlerën mesatare të ndryshores që shpjegohet. Kjo do të thotë, mesatarja aritmetike, e njohur për vetitë e saj të mira nga ligjet e numrave të mëdhenj, është gjithashtu një vlerësim i katrorëve më të vegjël - ai plotëson kriterin për shumën minimale të devijimeve në katror prej tij.
Shembull: regresion i thjeshtë (në çift).
Në rastin e regresionit linear të çiftuar, formulat e llogaritjes janë thjeshtuar (mund të bëni pa algjebër matricë):
Vetitë e vlerësimeve të OLS
Para së gjithash, vërejmë se për modelet lineare, vlerësimet e katrorëve më të vegjël janë vlerësime lineare, siç vijon nga formula e mësipërme. Për vlerësimet e paanshme OLS, është e nevojshme dhe e mjaftueshme të përmbushet kushti më i rëndësishëm i analizës së regresionit: pritshmëria matematikore e një gabimi të rastësishëm të kushtëzuar nga faktorët duhet të jetë e barabartë me zero. Ky kusht plotësohet, veçanërisht nëse
- pritshmëria matematikore e gabimeve të rastësishme është zero, dhe
- faktorët dhe gabimet e rastësishme janë variabla të rastësishme të pavarura.
Kushti i dytë - gjendja e faktorëve ekzogjenë - është thelbësor. Nëse kjo pronë nuk është e kënaqur, atëherë mund të supozojmë se pothuajse çdo vlerësim do të jetë jashtëzakonisht i pakënaqshëm: ato as nuk do të jenë të qëndrueshme (d.m.th., edhe një sasi shumë e madhe e të dhënave nuk lejon marrjen e vlerësimeve cilësore në këtë rast). Në rastin klasik, bëhet një supozim më i fortë për determinizmin e faktorëve, në ndryshim nga një gabim i rastësishëm, që automatikisht do të thotë se kushti ekzogjen është i plotësuar. Në rastin e përgjithshëm, për konsistencën e vlerësimeve, mjafton të plotësohet kushti i ekzogjenitetit së bashku me konvergjencën e matricës me një matricë jo të vetme me një rritje të madhësisë së mostrës deri në pafundësi.
Në mënyrë që, përveç konsistencës dhe paanshmërisë, vlerësimet e katrorëve më të vegjël (të zakonshëm) të jenë gjithashtu efektivë (më të mirët në klasën e vlerësimeve lineare të paanshme), është e nevojshme të plotësohen vetitë shtesë të një gabimi të rastësishëm:
Këto supozime mund të formulohen për matricën e kovariancës së vektorit të gabimit të rastësishëm
Një model linear që plotëson këto kushte quhet klasike. Vlerësimet OLS për regresionin linear klasik janë vlerësime të paanshme, të qëndrueshme dhe më efikase në klasën e të gjitha vlerësimeve lineare të paanshme (në literaturën angleze, shkurtimi përdoret ndonjëherë blu (Vlerësuesi më i mirë linear i pabazuar) është vlerësimi më i mirë linear i paanshëm; në literaturën vendase, më shpesh citohet teorema Gauss-Markov). Siç është e lehtë të tregohet, matrica e kovariancës së vektorit të vlerësimit të koeficientit do të jetë e barabartë me:
Katroret më të vegjël të përgjithësuar
Metoda e katrorëve më të vegjël lejon një përgjithësim të gjerë. Në vend që të minimizohet shuma e katrorëve të mbetjeve, mund të minimizohet një formë kuadratike pozitive e caktuar e vektorit të mbetur, ku është një matricë simetrike pozitive e peshës së caktuar. Katroret më të vegjël të zakonshëm janë një rast i veçantë i kësaj qasjeje, kur matrica e peshës është proporcionale me matricën e identitetit. Siç dihet nga teoria e matricave (ose operatorëve) simetrike, ka një dekompozim për matrica të tilla. Prandaj, funksioni i specifikuar mund të përfaqësohet si më poshtë, domethënë, ky funksional mund të përfaqësohet si shuma e katrorëve të disa "mbetjeve" të transformuara. Kështu, ne mund të dallojmë një klasë të metodave të katrorëve më të vegjël - metodat LS (Katroret më të vegjël).
Është vërtetuar (teorema e Aitken) se për një model të përgjithësuar të regresionit linear (në të cilin nuk vendosen kufizime në matricën e kovariancës së gabimeve të rastit), më efektive (në klasën e vlerësimeve lineare të paanshme) janë vlerësimet e të ashtuquajturave. OLS e përgjithësuar (OMNK, GLS - katrorët më të vegjël të përgjithësuar)- Metoda LS me matricë peshe të barabartë me matricën e kovariancës së anasjelltë të gabimeve të rastit: .
Mund të tregohet se formula për GLS-vlerësimet e parametrave të modelit linear ka formën
Matrica e kovariancës së këtyre vlerësimeve, përkatësisht, do të jetë e barabartë me
Në fakt, thelbi i OLS qëndron në një transformim të caktuar (linear) (P) të të dhënave origjinale dhe aplikimin e katrorëve më të vegjël të zakonshëm në të dhënat e transformuara. Qëllimi i këtij transformimi është që për të dhënat e transformuara, gabimet e rastësishme tashmë plotësojnë supozimet klasike.
Sheshet më të vogla të peshuara
Në rastin e një matrice të peshës diagonale (dhe rrjedhimisht matricës së kovariancës së gabimeve të rastit), kemi të ashtuquajturat katrorët më të vegjël të ponderuar (WLS - Katroret më të vogla të ponderuara). Në këtë rast, shuma e ponderuar e katrorëve të mbetjeve të modelit minimizohet, domethënë çdo vëzhgim merr një "peshë" që është në përpjesëtim të zhdrejtë me variancën e gabimit të rastit në këtë vëzhgim: . Në fakt, të dhënat transformohen duke peshuar vëzhgimet (duke pjesëtuar me një sasi proporcionale me devijimin standard të supozuar të gabimeve të rastit), dhe katrorët më të vegjël normalë aplikohen në të dhënat e ponderuara.
Disa raste të veçanta të aplikimit të LSM në praktikë
Përafrim linear
Konsideroni rastin kur, si rezultat i studimit të varësisë së një sasie të caktuar skalare nga një sasi e caktuar skalare (Kjo mund të jetë, për shembull, varësia e tensionit nga forca aktuale: , ku është një vlerë konstante, rezistenca e përcjellësit ), u matën këto sasi, si rezultat i të cilave vlerat dhe vlerat e tyre përkatëse. Të dhënat e matjes duhet të regjistrohen në një tabelë.
Tabela. Rezultatet e matjes.
| Matja Nr. | ||
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
Pyetja tingëllon si kjo: cila vlerë e koeficientit mund të zgjidhet për të përshkruar më së miri varësinë? Sipas katrorëve më të vegjël, kjo vlerë duhet të jetë e tillë që shuma e devijimeve në katror të vlerave nga vlerat
ishte minimale
Shuma e devijimeve në katror ka një ekstrem - një minimum, i cili na lejon të përdorim këtë formulë. Le të gjejmë vlerën e koeficientit nga kjo formulë. Për ta bërë këtë, ne transformojmë anën e saj të majtë si më poshtë:
Formula e fundit na lejon të gjejmë vlerën e koeficientit , i cili kërkohej në problem.
Histori
Deri në fillim të shekullit XIX. shkencëtarët nuk kishin rregulla të caktuara për zgjidhjen e një sistemi ekuacionesh në të cilin numri i të panjohurave është më i vogël se numri i ekuacioneve; Deri në atë kohë përdoreshin metoda të veçanta, varësisht nga lloji i ekuacioneve dhe nga zgjuarsia e kalkulatorëve, dhe për këtë arsye kalkulatorë të ndryshëm, duke u nisur nga të njëjtat të dhëna vëzhguese, dolën në përfundime të ndryshme. Gauss (1795) vlerësohet me aplikimin e parë të metodës, dhe Lezhandre (1805) në mënyrë të pavarur e zbuloi dhe e publikoi atë me emrin e tij modern (fr. Method des moindres quarres ) . Laplace e lidhi metodën me teorinë e probabilitetit, dhe matematikani amerikan Adrain (1808) shqyrtoi aplikimet e saj probabilistike. Metoda është e përhapur dhe e përmirësuar nga kërkimet e mëtejshme nga Encke, Bessel, Hansen dhe të tjerë.
Përdorimi alternativ i MNC-ve
Ideja e metodës së katrorëve më të vegjël mund të përdoret edhe në raste të tjera që nuk lidhen drejtpërdrejt me analizën e regresionit. Fakti është se shuma e katrorëve është një nga matjet më të zakonshme të afërsisë për vektorët (metrika Euklidiane në hapësirat me dimensione të fundme).
Një aplikim është "zgjidhja" e sistemeve të ekuacioneve lineare në të cilat numri i ekuacioneve është më i madh se numri i ndryshoreve.
ku matrica nuk është katrore, por drejtkëndore.
Një sistem i tillë ekuacionesh, në rastin e përgjithshëm, nuk ka zgjidhje (nëse rangu është në të vërtetë më i madh se numri i ndryshoreve). Prandaj, ky sistem mund të "zgjidhet" vetëm në kuptimin e zgjedhjes së një vektori të tillë në mënyrë që të minimizohet "distanca" midis vektorëve dhe . Për ta bërë këtë, mund të aplikoni kriterin për minimizimin e shumës së diferencave në katror të pjesëve të majta dhe të djathta të ekuacioneve të sistemit, domethënë . Është e lehtë të tregohet se zgjidhja e këtij problemi të minimizimit çon në zgjidhjen e sistemit të mëposhtëm të ekuacioneve