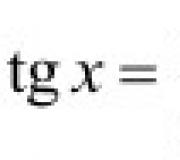Como encontrar a derivada de uma soma. Derivada de uma soma algébrica de funções

A operação de encontrar a derivada é chamada de diferenciação.

Como resultado da resolução de problemas para encontrar derivadas das funções mais simples (e não muito simples), definindo a derivada como o limite da razão entre o incremento e o incremento do argumento, apareceu uma tabela de derivadas e exatamente certas regras diferenciação. Os primeiros a trabalhar na área de determinação de derivadas foram Isaac Newton (1643-1727) e Gottfried Wilhelm Leibniz (1646-1716).

Portanto, em nosso tempo, para encontrar a derivada de qualquer função, não é necessário calcular o limite acima mencionado da razão entre o incremento da função e o incremento do argumento, mas você só precisa usar a tabela de derivadas e as regras de diferenciação. O algoritmo a seguir é adequado para encontrar a derivada.

Para encontrar a derivada, você precisa de uma expressão sob o sinal principal dividir funções simples em componentes e determinar quais ações (produto, soma, quociente) essas funções estão relacionadas. A seguir, encontramos as derivadas das funções elementares na tabela de derivadas, e as fórmulas para as derivadas do produto, soma e quociente - nas regras de diferenciação. A tabela de derivadas e as regras de diferenciação são fornecidas após os dois primeiros exemplos.

Exemplo 1. Encontre a derivada de uma função

Solução. A partir das regras de diferenciação descobrimos que a derivada de uma soma de funções é a soma das derivadas de funções, ou seja,

Na tabela de derivadas descobrimos que a derivada de “x” é igual a um, e a derivada do seno é igual ao cosseno. Substituímos esses valores na soma das derivadas e encontramos a derivada exigida pela condição do problema:

Exemplo 2. Encontre a derivada de uma função

Solução. Diferenciamos como derivada de uma soma em que o segundo termo tem um fator constante pode ser retirado do sinal da derivada:

Se ainda surgirem dúvidas sobre a origem de algo, elas geralmente serão esclarecidas depois de se familiarizar com a tabela de derivadas e as regras mais simples de diferenciação. Estamos passando para eles agora.

Tabela de derivadas de funções simples

1. Derivada de uma constante (número). Qualquer número (1, 2, 5, 200...) que esteja na expressão da função. Sempre igual a zero. É muito importante lembrar disso, pois muitas vezes é necessário
2. Derivada da variável independente. Na maioria das vezes "X". Sempre igual a um. Isso também é importante lembrar por muito tempo
3. Derivada de grau. Ao resolver problemas, você precisa converter raízes não quadradas em potências.
4. Derivada de uma variável elevada à potência -1
5. Derivada da raiz quadrada
6. Derivada do seno
7. Derivada do cosseno
8. Derivada da tangente
9. Derivada da cotangente
10. Derivada do arco seno
11. Derivada do arco cosseno
12. Derivada do arco tangente
13. Derivada do arco cotangente
14. Derivada do logaritmo natural
15. Derivada de uma função logarítmica
16. Derivada do expoente
17. Derivada de uma função exponencial

Regras de diferenciação

1. Derivada de uma soma ou diferença
2. Derivada do produto
2a. Derivada de uma expressão multiplicada por um fator constante
3. Derivada do quociente
4. Derivada de uma função complexa

Regra 1.Se as funções

são diferenciáveis ​​em algum ponto, então as funções são diferenciáveis ​​no mesmo ponto

e

aqueles. a derivada de uma soma algébrica de funções é igual à soma algébrica das derivadas dessas funções.

Consequência. Se duas funções diferenciáveis ​​diferem por um termo constante, então suas derivadas são iguais, ou seja

Regra 2.Se as funções

são diferenciáveis ​​em algum ponto, então seu produto é diferenciável no mesmo ponto

e

aqueles. A derivada do produto de duas funções é igual à soma dos produtos de cada uma dessas funções e a derivada da outra.

Corolário 1. O fator constante pode ser retirado do sinal da derivada:

Corolário 2. A derivada do produto de várias funções diferenciáveis ​​é igual à soma dos produtos da derivada de cada fator e de todos os outros.

Por exemplo, para três multiplicadores:

Regra 3.Se as funções

diferenciável em algum ponto E , então neste ponto seu quociente também é diferenciávelvocê/v e

aqueles. a derivada do quociente de duas funções é igual a uma fração, cujo numerador é a diferença entre os produtos do denominador e a derivada do numerador e o numerador e a derivada do denominador, e o denominador é o quadrado de o antigo numerador.

Onde procurar coisas em outras páginas

Ao encontrar a derivada de um produto e um quociente em problemas reais, é sempre necessário aplicar várias regras de diferenciação ao mesmo tempo, portanto mais exemplos para esses derivados - no artigo"Derivada do produto e quociente de funções".

Comente. Você não deve confundir uma constante (isto é, um número) como um termo em uma soma e como um fator constante! No caso de um termo, sua derivada é igual a zero e, no caso de um fator constante, é retirada do sinal das derivadas. Esse erro típico, que ocorre em Estado inicial estudando derivadas, mas como eles resolvem vários exemplos de uma e duas partes, o aluno médio não comete mais esse erro.

E se, ao diferenciar um produto ou quociente, você tiver um termo você"v, no qual você- um número, por exemplo, 2 ou 5, ou seja, uma constante, então a derivada desse número será igual a zero e, portanto, todo o termo será igual a zero (este caso é discutido no exemplo 10).

Outro erro comum- solução mecânica da derivada de uma função complexa como derivada de uma função simples. É por isso derivada de uma função complexa um artigo separado é dedicado. Mas primeiro aprenderemos a determinar derivadas de funções simples.

Ao longo do caminho, você não pode prescindir da transformação de expressões. Para fazer isso, pode ser necessário abrir o manual em novas janelas. Ações com poderes e raízes E Operações com frações .

Se você está procurando soluções para derivadas de frações com potências e raízes, ou seja, quando a função se parece com , depois siga a lição “Derivada de somas de frações com potências e raízes”.

Se você tem uma tarefa como , então você fará a lição “Derivadas de funções trigonométricas simples”.

Exemplos passo a passo - como encontrar a derivada

Exemplo 3. Encontre a derivada de uma função

Solução. Definimos as partes da expressão da função: toda a expressão representa um produto, e seus fatores são somas, na segunda das quais um dos termos contém um fator constante. Aplicamos a regra de diferenciação do produto: a derivada do produto de duas funções é igual à soma dos produtos de cada uma dessas funções pela derivada da outra:

A seguir, aplicamos a regra de diferenciação da soma: a derivada da soma algébrica das funções é igual à soma algébrica das derivadas dessas funções. No nosso caso, em cada soma o segundo termo possui um sinal negativo. Em cada soma vemos tanto uma variável independente, cuja derivada é igual a um, quanto uma constante (número), cuja derivada é igual a zero. Então, “X” se transforma em um e menos 5 se transforma em zero. Na segunda expressão, “x” é multiplicado por 2, então multiplicamos dois pela mesma unidade que a derivada de “x”. Obtemos os seguintes valores derivados:

Substituímos as derivadas encontradas na soma dos produtos e obtemos a derivada de toda a função exigida pela condição do problema:

Exemplo 4. Encontre a derivada de uma função

Solução. Somos obrigados a encontrar a derivada do quociente. Aplicamos a fórmula para diferenciar o quociente: a derivada do quociente de duas funções é igual a uma fração, cujo numerador é a diferença entre os produtos do denominador e a derivada do numerador e o numerador e a derivada do denominador, e o denominador é o quadrado do antigo numerador. Nós temos:

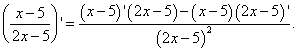
Já encontramos a derivada dos fatores no numerador no exemplo 2. Não esqueçamos também que o produto, que é o segundo fator no numerador no exemplo atual, é considerado com sinal de menos:

Se você está procurando soluções para problemas em que precisa encontrar a derivada de uma função, onde existe uma pilha contínua de raízes e potências, como, por exemplo, , então seja bem-vindo à aula "Derivada de somas de frações com potências e raízes" .

Se você precisa aprender mais sobre as derivadas de senos, cossenos, tangentes e outros funções trigonométricas, isto é, quando a função se parece com , então uma lição para você "Derivadas de funções trigonométricas simples" .

Exemplo 5. Encontre a derivada de uma função

Solução. Nesta função vemos um produto, um dos fatores do qual é Raiz quadrada da variável independente, cuja derivada vimos na tabela de derivadas. Usando a regra de diferenciação do produto e o valor tabular da derivada da raiz quadrada, obtemos:

Exemplo 6. Encontre a derivada de uma função

Solução. Nesta função vemos um quociente cujo dividendo é a raiz quadrada da variável independente. Utilizando a regra de diferenciação de quocientes, que repetimos e aplicamos no exemplo 4, e o valor tabulado da derivada da raiz quadrada, obtemos:

Para eliminar uma fração no numerador, multiplique o numerador e o denominador por .

Primeiro nível

Derivada de uma função. Guia abrangente (2019)

Vamos imaginar uma estrada reta passando por uma área montanhosa. Ou seja, sobe e desce, mas não vira à direita nem à esquerda. Se o eixo for direcionado horizontalmente ao longo da estrada e verticalmente, a linha da estrada será muito semelhante ao gráfico de alguma função contínua:

O eixo é um certo nível de altitude zero, na vida usamos o nível do mar como tal.

À medida que avançamos nessa estrada, também subimos ou descemos. Também podemos dizer: quando o argumento muda (movimento ao longo do eixo das abcissas), o valor da função muda (movimento ao longo do eixo das ordenadas). Agora vamos pensar em como determinar a “inclinação” da nossa estrada? Que tipo de valor poderia ser esse? É muito simples: quanto a altura mudará ao avançar uma certa distância. Na verdade, em diferentes trechos da estrada, avançando (ao longo do eixo x) um quilômetro, subiremos ou desceremos quantidades diferentes metros em relação ao nível do mar (ao longo do eixo das ordenadas).

Vamos denotar progresso (leia “delta x”).

A letra grega (delta) é comumente usada em matemática como um prefixo que significa "mudança". Isto é - isto é uma mudança na quantidade, - uma mudança; então, o que é? Isso mesmo, uma mudança de magnitude.

Importante: uma expressão é um todo único, uma variável. Nunca separe o “delta” do “x” ou de qualquer outra letra! Isto é, por exemplo, .

Então, avançamos, horizontalmente, por. Se compararmos a linha da estrada com o gráfico da função, como denotamos a subida? Certamente, . Ou seja, à medida que avançamos, subimos mais alto.

O valor é fácil de calcular: se no início estávamos em altura, e depois de nos movermos nos encontramos em altura, então. Se o ponto final for inferior ao ponto inicial, será negativo - isso significa que não estamos subindo, mas descendo.

Voltemos à "inclinação": este é um valor que mostra o quanto (íngreme) a altura aumenta ao avançar uma unidade de distância:

Suponhamos que em algum trecho da estrada, ao avançar um quilômetro, a estrada sobe um quilômetro. Então a inclinação neste local é igual. E se a estrada, ao avançar m, diminuísse km? Então a inclinação é igual.

Agora vamos olhar para o topo de uma colina. Se você pegar o início do trecho meio quilômetro antes do cume e o final meio quilômetro depois, verá que a altura é quase a mesma.

Ou seja, de acordo com a nossa lógica, verifica-se que a inclinação aqui é quase igual a zero, o que claramente não é verdade. A poucos quilômetros de distância, muita coisa pode mudar. É necessário considerar áreas menores para uma avaliação mais adequada e precisa da declividade. Por exemplo, se você medir a mudança na altura à medida que avança um metro, o resultado será muito mais preciso. Mas mesmo essa precisão pode não ser suficiente para nós - afinal, se houver um poste no meio da estrada, podemos simplesmente ultrapassá-lo. Que distância devemos escolher então? Centímetro? Milímetro? Menos é melhor!

EM Vida real Medir distâncias até o milímetro mais próximo é mais que suficiente. Mas os matemáticos sempre buscam a perfeição. Portanto, o conceito foi inventado infinitamente, ou seja, o valor absoluto é menor que qualquer número que possamos nomear. Por exemplo, você diz: um trilionésimo! Quanto menos? E você divide esse número por - e será ainda menor. E assim por diante. Se quisermos escrever que uma quantidade é infinitesimal, escrevemos assim: (lemos “x tende a zero”). É muito importante entender que esse número não é zero! Mas muito perto disso. Isso significa que você pode dividir por ele.

O conceito oposto a infinitesimal é infinitamente grande (). Você provavelmente já se deparou com isso quando estava trabalhando com desigualdades: esse número é módulo maior do que qualquer número que você possa imaginar. Se você encontrar o maior número possível, basta multiplicá-lo por dois e obterá um número ainda maior. E o infinito é ainda maior do que o que acontece. Na verdade, o infinitamente grande e o infinitamente pequeno são o inverso um do outro, isto é, at, e vice-versa: at.

Agora vamos voltar ao nosso caminho. A inclinação idealmente calculada é a inclinação calculada para um segmento infinitesimal do caminho, ou seja:

Observo que com um deslocamento infinitesimal, a mudança na altura também será infinitesimal. Mas deixe-me lembrá-lo de que infinitesimal não significa igual a zero. Se você dividir números infinitesimais entre si, poderá obter um número completamente comum, por exemplo, . Ou seja, um valor pequeno pode ser exatamente vezes maior que outro.

Para que serve tudo isso? A estrada, a inclinação... Não vamos fazer um rali de automóveis, mas vamos ensinar matemática. E em matemática tudo é exatamente igual, só que com um nome diferente.

Conceito de derivada

A derivada de uma função é a razão entre o incremento da função e o incremento do argumento para um incremento infinitesimal do argumento.

Incrementalmente em matemática eles chamam de mudança. A extensão em que o argumento () muda à medida que se move ao longo do eixo é chamada incremento de argumento e é designado o quanto a função (altura) mudou ao avançar ao longo do eixo por uma distância é chamada. incremento de função e é designado.

Portanto, a derivada de uma função é a razão para quando. Denotamos a derivada com a mesma letra da função, apenas com um primo no canto superior direito: ou simplesmente. Então, vamos escrever a fórmula da derivada usando estas notações:

Como na analogia com a estrada, aqui quando a função aumenta, a derivada é positiva, e quando diminui, é negativa.

A derivada pode ser igual a zero? Certamente. Por exemplo, se estivermos dirigindo em uma estrada plana e horizontal, a inclinação será zero. E é verdade, a altura não muda em nada. O mesmo acontece com a derivada: a derivada de uma função constante (constante) é igual a zero:

já que o incremento de tal função é igual a zero para qualquer.

Vamos lembrar o exemplo do topo da colina. Descobriu-se que era possível organizar as extremidades do segmento ao longo lados diferentes de cima, para que a altura nas extremidades seja a mesma, ou seja, o segmento seja paralelo ao eixo:

Mas segmentos grandes são um sinal de medição imprecisa. Levantaremos nosso segmento paralelo a ele mesmo, então seu comprimento diminuirá.

Eventualmente, quando estivermos infinitamente próximos do topo, o comprimento do segmento se tornará infinitesimal. Mas, ao mesmo tempo, permaneceu paralelo ao eixo, ou seja, a diferença de alturas em suas extremidades é igual a zero (não tende, mas é igual). Então a derivada

Isto pode ser entendido desta forma: quando estamos no topo, um pequeno deslocamento para a esquerda ou para a direita altera a nossa altura de forma insignificante.

Há também uma explicação puramente algébrica: à esquerda do vértice a função aumenta e à direita diminui. Como descobrimos anteriormente, quando uma função aumenta, a derivada é positiva e, quando diminui, é negativa. Mas muda suavemente, sem saltos (já que a estrada não muda bruscamente de inclinação em nenhum lugar). Portanto, deve haver entre valores negativos e positivos. Será onde a função não aumenta nem diminui - no ponto vértice.

O mesmo se aplica ao vale (a área onde a função à esquerda diminui e à direita aumenta):

Um pouco mais sobre incrementos.

Então mudamos o argumento para magnitude. Mudamos a partir de que valor? O que isso (o argumento) se tornou agora? Podemos escolher qualquer ponto e agora vamos dançar a partir dele.

Considere um ponto com uma coordenada. O valor da função nele é igual. Então fazemos o mesmo incremento: aumentamos a coordenada em. Qual é o argumento agora? Muito fácil: . Qual é o valor da função agora? Para onde vai o argumento, também vai a função: . E quanto ao incremento de função? Nada de novo: este ainda é o valor pelo qual a função mudou:

Pratique encontrar incrementos:

1. Encontre o incremento da função no ponto em que o incremento do argumento é igual a.
2. O mesmo vale para a função em um ponto.

Soluções:

EM pontos diferentes com o mesmo incremento de argumento, o incremento da função será diferente. Isso significa que a derivada em cada ponto é diferente (discutimos isso no início - a inclinação da estrada é diferente em diferentes pontos). Portanto, quando escrevemos uma derivada, devemos indicar em que ponto:

Função liga-desliga.

Uma função de potência é uma função onde o argumento é até certo ponto (lógico, certo?).

Além disso - em qualquer medida: .

O caso mais simples- é quando o expoente:

Vamos encontrar sua derivada em um ponto. Vamos relembrar a definição de derivada:

Portanto, o argumento muda de para. Qual é o incremento da função?

Incremento é isso. Mas uma função em qualquer ponto é igual ao seu argumento. É por isso:

A derivada é igual a:

A derivada de é igual a:

b) Agora considere função quadrática (): .

Agora vamos lembrar disso. Isso significa que o valor do incremento pode ser desprezado, pois é infinitesimal e, portanto, insignificante em relação ao outro termo:

Então, criamos outra regra:

c) Continuamos a série lógica: .

Esta expressão pode ser simplificada de diferentes maneiras: abra o primeiro colchete usando a fórmula de multiplicação abreviada do cubo da soma, ou fatore a expressão inteira usando a fórmula da diferença de cubos. Tente fazer isso sozinho usando qualquer um dos métodos sugeridos.

Então, obtive o seguinte:

E novamente vamos lembrar disso. Isso significa que podemos desprezar todos os termos que contenham:

Nós temos: .

d) Regras semelhantes podem ser obtidas para grandes potências:

e) Acontece que esta regra pode ser generalizada para uma função potência com um expoente arbitrário, nem mesmo um número inteiro:

A regra pode ser formulada nas palavras: “o grau é apresentado como um coeficiente e depois reduzido por.”

Provaremos esta regra mais tarde (quase no final). Agora vamos ver alguns exemplos. Encontre a derivada das funções:

1. (de duas formas: por fórmula e usando a definição de derivada - calculando o incremento da função);

1. . Acredite ou não, esta é uma função de poder. Se você tiver perguntas como “Como é isso? Cadê o diploma?”, lembre-se do tópico “”!
   Sim, sim, a raiz também é um grau, apenas fracionário: .
   Isto significa que a nossa raiz quadrada é apenas uma potência com um expoente:
   .
   Procuramos a derivada usando a fórmula aprendida recentemente:

   Se neste ponto não ficar claro novamente, repita o tópico “”!!! (cerca de um grau com um expoente negativo)

2. . Agora o expoente:

   E agora através da definição (já esqueceu?):
   ;
   .
   Agora, como sempre, negligenciamos o termo que contém:
   .

3. . Combinação de casos anteriores: .

Funções trigonométricas.

Aqui usaremos um fato da matemática superior:

Com expressão.

Você aprenderá a prova no primeiro ano do instituto (e para chegar lá é preciso passar bem no Exame Estadual Unificado). Agora vou apenas mostrar graficamente:

Vemos que quando a função não existe, um ponto no gráfico é cortado. Mas quanto mais próximo do valor, mais próxima a função está disso.

Além disso, você pode verificar esta regra usando uma calculadora. Sim, sim, não seja tímido, pegue uma calculadora, ainda não estamos no Exame Estadual Unificado.

Então vamos tentar: ;

Não se esqueça de mudar sua calculadora para o modo Radianos!

etc. Vemos que quanto menos, mais valor mais próximo Relação para

a) Considere a função. Como sempre, vamos encontrar seu incremento:

Vamos transformar a diferença de senos em um produto. Para isso, utilizamos a fórmula (lembre-se do tópico “”): .

Agora a derivada:

Vamos fazer uma substituição: . Então para infinitesimal também é infinitesimal: . A expressão para assume a forma:

E agora lembramos disso com a expressão. E também, e se uma quantidade infinitesimal puder ser desprezada na soma (isto é, em).

Assim, obtemos a seguinte regra: a derivada do seno é igual ao cosseno:

Estas são derivadas básicas (“tabulares”). Aqui estão eles em uma lista:

Posteriormente adicionaremos mais alguns a eles, mas estes são os mais importantes, pois são usados ​​com mais frequência.

Prática:

1. Encontre a derivada da função em um ponto;
2. Encontre a derivada da função.

Soluções:

1. Primeiro, vamos encontrar a derivada em visão geral e, em seguida, substitua seu valor:
   ;
   .
2. Aqui temos algo semelhante a uma função de potência. Vamos tentar trazê-la para
   visualização normal:
   .
   Ótimo, agora você pode usar a fórmula:
   .
   .
3. . Eeeeeee….. O que é isso????

Ok, você está certo, ainda não sabemos como encontrar essas derivadas. Aqui temos uma combinação de vários tipos de funções. Para trabalhar com eles, você precisa aprender mais algumas regras:

Expoente e logaritmo natural.

Existe uma função em matemática cuja derivada para qualquer valor é igual ao valor da própria função ao mesmo tempo. É chamado de “expoente” e é uma função exponencial

A base desta função é uma constante - é infinita decimal, isto é, um número irracional (como). É chamado de “número de Euler”, por isso é indicado por uma letra.

Então, a regra:

Muito fácil de lembrar.

Bem, não vamos longe, vamos considerar imediatamente a função inversa. Qual função é o inverso da função exponencial? Logaritmo:

No nosso caso, a base é o número:

Tal logaritmo (isto é, um logaritmo com base) é chamado de “natural” e usamos uma notação especial para ele: em vez disso, escrevemos.

A que é igual? Claro, .

A derivada do logaritmo natural também é muito simples:

Exemplos:

1. Encontre a derivada da função.
2. Qual é a derivada da função?

Respostas: Expositor e Logaritmo natural- as funções são exclusivamente simples em termos de derivadas. Funções exponenciais e logarítmicas com qualquer outra base terão uma derivada diferente, que analisaremos mais tarde, após vamos passar pelas regras diferenciação.

Regras de diferenciação

Regras de quê? De novo um novo mandato, de novo?!...

Diferenciaçãoé o processo de encontrar a derivada.

Isso é tudo. Como mais você pode chamar esse processo em uma palavra? Não derivada... Os matemáticos chamam o diferencial de o mesmo incremento de uma função em. Este termo vem do latim Differentia - diferença. Aqui.

Ao derivar todas essas regras, usaremos duas funções, por exemplo, e. Também precisaremos de fórmulas para seus incrementos:

Existem 5 regras no total.

A constante é retirada do sinal da derivada.

Se - algum número constante (constante), então.

Obviamente, essa regra também funciona para a diferença: .

Vamos provar isso. Deixe estar, ou mais simples.

Exemplos.

Encontre as derivadas das funções:

1. em um ponto;
2. em um ponto;
3. em um ponto;
4. no ponto.

Soluções:

1. (a derivada é igual em todos os pontos, pois é uma função linear, lembra?);

Derivado do produto

Tudo é semelhante aqui: vamos introduzir uma nova função e encontrar seu incremento:

Derivado:

Exemplos:

1. Encontre as derivadas das funções e;
2. Encontre a derivada da função em um ponto.

Soluções:

Derivada de uma função exponencial

Agora seu conhecimento é suficiente para aprender como encontrar a derivada de qualquer função exponencial, e não apenas de expoentes (já esqueceu o que é isso?).

Então, onde está algum número.

Já conhecemos a derivada da função, então vamos tentar reduzir nossa função a uma nova base:

Para isso usaremos regra simples: . Então:

Bem, funcionou. Agora tente encontrar a derivada e não esqueça que esta função é complexa.

Ocorrido?

Aqui, verifique você mesmo:

A fórmula acabou sendo muito parecida com a derivada de um expoente: como estava, continua a mesma, apareceu apenas um fator, que é apenas um número, mas não uma variável.

Exemplos:
Encontre as derivadas das funções:

Respostas:

Este é apenas um número que não pode ser calculado sem calculadora, ou seja, não pode mais ser anotado de forma simples. Portanto, deixamos desta forma na resposta.

Derivada de uma função logarítmica

É semelhante aqui: você já conhece a derivada do logaritmo natural:

Portanto, para encontrar um logaritmo arbitrário com base diferente, por exemplo:

Precisamos reduzir este logaritmo à base. Como você muda a base de um logaritmo? Espero que você se lembre desta fórmula:

Só agora escreveremos:

O denominador é simplesmente uma constante (um número constante, sem variável). A derivada é obtida de forma muito simples:

Derivadas de funções exponenciais e logarítmicas quase nunca são encontradas no Exame de Estado Unificado, mas não será supérfluo conhecê-las.

Derivada de uma função complexa.

O que é uma “função complexa”? Não, isso não é um logaritmo e nem um arco tangente. Essas funções podem ser difíceis de entender (embora se você achar o logaritmo difícil, leia o tópico “Logaritmos” e você ficará bem), mas do ponto de vista matemático, a palavra “complexo” não significa “difícil”.

Imagine uma pequena esteira rolante: duas pessoas estão sentadas e realizando algumas ações com alguns objetos. Por exemplo, o primeiro embrulha uma barra de chocolate em uma embalagem e o segundo a amarra com uma fita. O resultado é um objeto composto: uma barra de chocolate embrulhada e amarrada com uma fita. Para comer uma barra de chocolate, você precisa seguir os passos inversos ordem reversa.

Vamos criar um pipeline matemático semelhante: primeiro encontraremos o cosseno de um número e depois elevaremos ao quadrado o número resultante. Então, nos é dado um número (chocolate), eu encontro seu cosseno (invólucro), e então você eleva ao quadrado o que consegui (amarre com uma fita). O que aconteceu? Função. Isto é um exemplo função complexa: quando, para encontrar o seu valor, realizamos a primeira ação diretamente com a variável, e depois uma segunda ação com o que resultou da primeira.

Podemos facilmente fazer os mesmos passos na ordem inversa: primeiro você eleva ao quadrado e depois procuro o cosseno do número resultante: . É fácil adivinhar que o resultado quase sempre será diferente. Recurso importante funções complexas: quando a ordem das ações muda, a função muda.

Em outras palavras, uma função complexa é uma função cujo argumento é outra função: .

Para o primeiro exemplo, .

Segundo exemplo: (mesma coisa). .

A ação que realizarmos por último será chamada função "externa", e a ação executada primeiro - respectivamente função "interna"(são nomes informais, utilizo-os apenas para explicar o material em linguagem simples).

Tente determinar por si mesmo qual função é externa e qual é interna:

Respostas: Separar funções internas e externas é muito semelhante a alterar variáveis: por exemplo, em uma função

1. Que ação realizaremos primeiro? Primeiro vamos calcular o seno e só depois elevá-lo ao cubo. Isso significa que é uma função interna, mas externa.
   E a função original é a sua composição: .
2. Interno: ; externo: .
   Exame: .
3. Interno: ; externo: .
   Exame: .
4. Interno: ; externo: .
   Exame: .
5. Interno: ; externo: .
   Exame: .

Mudamos variáveis ​​e obtemos uma função.

Bom, agora vamos extrair nossa barra de chocolate e procurar a derivada. O procedimento é sempre inverso: primeiro procuramos a derivada da função externa, depois multiplicamos o resultado pela derivada da função interna. Em relação ao exemplo original, fica assim:

Outro exemplo:

Então, vamos finalmente formular a regra oficial:

Algoritmo para encontrar a derivada de uma função complexa:

Parece simples, certo?

Vamos verificar com exemplos:

Soluções:

1) Interno: ;

Externo: ;

2) Interno: ;

(Só não tente cortar agora! Não sai nada do cosseno, lembra?)

3) Interno: ;

Externo: ;

Fica imediatamente claro que se trata de uma função complexa de três níveis: afinal, esta já é uma função complexa em si, e dela também extraímos a raiz, ou seja, realizamos a terceira ação (colocamos o chocolate em um embalagem e com fita na maleta). Mas não há motivo para ter medo: ainda iremos “desempacotar” esta função na mesma ordem de sempre: do final.

Ou seja, primeiro diferenciamos a raiz, depois o cosseno e só depois a expressão entre colchetes. E então multiplicamos tudo.

Nesses casos, é conveniente numerar as ações. Ou seja, vamos imaginar o que sabemos. Em que ordem realizaremos ações para calcular o valor desta expressão? Vejamos um exemplo:

Quanto mais tarde a ação for executada, mais “externa” será a função correspondente. A sequência de ações é a mesma de antes:

Aqui o aninhamento é geralmente de 4 níveis. Vamos determinar a ordem de ação.

1. Expressão radical. .

2. Raiz. .

3. Seno. .

4. Quadrado. .

5. Juntando tudo:

DERIVADO. BREVEMENTE SOBRE AS COISAS PRINCIPAIS

Derivada de uma função- a razão entre o incremento da função e o incremento do argumento para um incremento infinitesimal do argumento:

Derivados básicos:

Regras de diferenciação:

A constante é retirada do sinal de derivada:

Derivada da soma:

Derivado do produto:

Derivada do quociente:

Derivada de uma função complexa:

Algoritmo para encontrar a derivada de uma função complexa:

1. Definimos a função “interna” e encontramos sua derivada.
2. Definimos a função “externa” e encontramos sua derivada.
3. Multiplicamos os resultados do primeiro e do segundo pontos.

Questões do exame da disciplina acadêmica “Elementos de Matemática Superior”

para a especialidade 230115 “Programação em sistemas informáticos”

Ano letivo 2012\2013.

Matrizes e operações sobre elas.

(SOBRE. Uma matriz zero é uma matriz cujos elementos são todos iguais a 0.

SOBRE. Duas matrizes de mesma dimensão mxn são chamadas igual, se no cruzamento i-ésima linha e a j-ésima coluna em uma e outra matriz contém o mesmo número; eu=1, 2, ..., m ; j=1, 2, ..., n .

Deixar A= (a ij) é alguma matriz eg é um número arbitrário, então g A= (g a ij), ou seja, quando a matriz A é multiplicada pelo número g, todos os números que compõem a matriz A são multiplicados pelo número g.

Sejam A e B matrizes da mesma dimensão A = (a ij), B = (b ij), então sua soma A + B é a matriz C = (c ij) da mesma dimensão, determinada a partir da fórmula c ij = a ij + b ij, ou seja, ao somar duas matrizes, os números nelas localizados de forma idêntica são somados aos pares.

A matriz A pode ser multiplicada pela matriz B, ou seja, a matriz C = AB pode ser encontrada se o número de colunas n da matriz A for igual ao número de linhas da matriz B, e a matriz C terá tantas linhas quanto a matriz A possui linhas e tantas colunas quanto a matriz possui colunas B. Cada elemento da matriz C é definido por uma fórmula.

Elemento c ij da matriz produto C igual à soma produtos dos elementos da i-ésima linha da primeira matriz fatorial e dos elementos correspondentes da j-ésima coluna da segunda matriz fatorial.

O conceito de determinante e suas propriedades.

Este termo tem outros significados, veja Determinante (valores) .

Determinante(ou determinante) - um dos conceitos básicos álgebra Linear. Determinante matrizesé polinomial dos elementos de uma matriz quadrada (ou seja, aquela em que o número de linhas e colunas é igual). Em geral matriz pode ser definido sobre qualquer comutativo anel, neste caso o determinante será um elemento do mesmo anel.

PROPRIEDADE 1. O valor do determinante não mudará se todas as suas linhas forem substituídas por colunas, e cada linha for substituída por uma coluna com o mesmo número, ou seja

PROPRIEDADE 2. Reorganizar duas colunas ou duas linhas de um determinante equivale a multiplicá-lo por -1.

PROPRIEDADE 3. Se o determinante tiver duas colunas idênticas ou duas linhas idênticas, então é igual a zero.

PROPRIEDADE 4. Multiplicar todos os elementos de uma coluna ou linha de um determinante por qualquer número k é equivalente a multiplicar o determinante por este número k.

PROPRIEDADE 5. Se todos os elementos de alguma coluna ou linha forem iguais a zero, então o próprio determinante é igual a zero. Esta propriedade é um caso especial da anterior (para k=0).

PROPRIEDADE 6. Se os elementos correspondentes de duas colunas ou duas linhas de um determinante são proporcionais, então o determinante é igual a zero.

PROPRIEDADE 7. Se cada elemento da enésima coluna ou enésima linha do determinante for a soma de dois termos, então o determinante pode ser representado como a soma de dois determinantes, dos quais um na enésima coluna ou, respectivamente, na enésima linha contém o primeiro dos termos mencionados e a outra - o segundo; os elementos que estão nos demais lugares são iguais para os marcos dos três determinantes.

PROPRIEDADE 8. Se aos elementos de uma determinada coluna (ou alguma linha) somarmos os elementos correspondentes de outra coluna (ou outra linha), multiplicados por qualquer fator comum, então o valor do determinante não mudará. Por exemplo. Outras propriedades dos determinantes estão relacionadas ao conceito de complemento algébrico e menor. O menor de um elemento é um determinante obtido de um determinado elemento riscando a linha e a coluna na intersecção das quais esse elemento está localizado.

O complemento algébrico de qualquer elemento do determinante é igual ao menor deste elemento, tomado com seu sinal se a soma dos números da linha e da coluna na interseção da qual o elemento está localizado for um número par, e com o sinal oposto se este número for ímpar.

Denotaremos o complemento algébrico de um elemento por uma letra maiúscula com o mesmo nome e o mesmo número da letra que denota o próprio elemento.

PROPRIEDADE 9. O determinante é igual à soma dos produtos dos elementos de qualquer coluna (ou linha) pelos seus complementos algébricos. Em outras palavras, as seguintes igualdades são válidas:

Cálculo de determinantes.

O cálculo dos determinantes é baseado em suas propriedades conhecidas, que se aplicam a determinantes de todas as ordens. Estas são as propriedades:

1. Se você reorganizar duas linhas (ou duas colunas) do determinante, o determinante mudará de sinal.

2. Se os elementos correspondentes de duas colunas (ou duas linhas) do determinante são iguais ou proporcionais, então o determinante é igual a zero.

3. O valor do determinante não mudará se você trocar as linhas e colunas, mantendo sua ordem.

4. Se todos os elementos de uma linha (ou coluna) tiverem um fator comum, então ele pode ser retirado do sinal determinante.

5. O valor do determinante não mudará se os elementos correspondentes de outra linha (ou coluna) forem somados aos elementos de uma linha (ou coluna), multiplicados pelo mesmo número. Para determinantes de terceira ordem, esta propriedade pode ser escrita, por exemplo, assim:

6. O determinante de segunda ordem é calculado pela fórmula

7. O determinante de terceira ordem é calculado pela fórmula

Existe um esquema conveniente para calcular o determinante de terceira ordem (ver Fig. 1 e Fig. 2).

De acordo com o diagrama mostrado na Fig. 1, os produtos dos elementos conectados são tomados com sinal próprio e conforme diagrama da Fig. 2 - com reverso. O valor do determinante é igual à soma algébrica dos seis produtos resultantes.

Sistemas de equações lineares. Conceitos e definições básicas.

Sistemasenhor equações algébricas lineares Comn desconhecido(ou, sistema linear, Também usado abreviação SLAU)V álgebra Linearé um sistema de equações da forma

Sistema equações lineares de três variáveis ​​​​determina o conjunto aviões. O ponto de intersecção é a solução.

Aqui está o número de equações e é o número de incógnitas. x 1 , x 2 , …, x n- incógnitas que precisam ser determinadas. a 11 , a 12 , …, a homem- coeficientes do sistema - e b 1 , b 2 , … b eu- membros gratuitos - são considerados conhecidos . Índices de coeficiente ( a eu j) sistemas denotam números de equações ( eu) e desconhecido ( j), em que este coeficiente se situa, respectivamente .

O sistema (1) é chamado homogêneo , se todos os seus termos livres forem iguais a zero ( b 1 = b 2 = … = b eu= 0), caso contrário - heterogêneo.

O sistema (1) é chamado quadrado , se número eu equações iguais ao número n desconhecido.

Solução sistemas (1) - conjunto n números c 1 , c 2 , …, c n, de modo que a substituição de cada c eu em vez de x eu no sistema (1) transforma todas as suas equações em identidades.

O sistema (1) é chamado articulação , se tiver pelo menos uma solução, e não articulado, se ela não tiver uma solução única.

Um sistema conjunto do tipo (1) pode ter uma ou mais soluções.

Soluções c 1 (1) , c 2 (1) , …, c n(1) e c 1 (2) , c 2 (2) , …, c n(2) sistemas conjuntos da forma (1) são chamados vários, se pelo menos uma das igualdades for violada:

Um sistema conjunto da forma (1) é chamado certo , se tiver uma solução única; se tiver pelo menos duas soluções diferentes, então é chamado incerto. Se houver mais equações do que incógnitas, é chamado redefinido .

Métodos de resolução de sistemas de equações lineares (método de Cramer e Gauss).

Método Gaussiano - método de solução clássico sistemas de equações algébricas lineares(SLAU). Este é o método de eliminação sequencial variáveis, quando, por meio de transformações elementares, um sistema de equações é reduzido a um sistema triangular equivalente, a partir do qual todas as outras variáveis ​​​​são encontradas sequencialmente, começando pelas últimas (por número) variáveis .

Método de Cramer (regra de Cramer)- método de resolução de quadrados sistemas de equações algébricas lineares com diferente de zero determinante matriz principal(e para tais equações existe uma solução única). Chamado pelo nome Gabriel Kramer(1704–1752), que inventou o método.

Vetores. Operações lineares sobre eles.

Um vetor é um segmento direcionado. Se o início de um vetor estiver no ponto A e o final estiver no ponto B, então o vetor é designado AB. Se o início e o fim do vetor não forem indicados, ele será indicado por uma letra minúscula Alfabeto latino a, b, c,…. BA denota um vetor direcionado oposto ao vetor AB. Um vetor cujo início e fim coincidem é chamado zero e é denotado por ō. Sua direção é incerta.

O comprimento ou módulo de um vetor é a distância entre seu início e seu fim. Registros |AB| e |a| denotam os módulos dos vetores AB e a.

Os vetores são chamados colineares se forem paralelos à mesma reta, e coplanares se forem paralelos ao mesmo plano.

Dois vetores são considerados iguais se forem colineares, tiverem a mesma direção e comprimentos iguais.

As operações lineares em vetores incluem:

1) multiplicação de um vetor por um número (O produto de um vetor a e um número α é um vetor denotado α∙a. (ou vice-versa a∙α), cujo módulo é igual a |α a| =| α||a|, e a direção coincide com a direção do vetor a, se α>0, e o oposto se α< 0.

2) adição de vetores (A soma dos vetores é um vetor, denotado por , cujo início está no início do primeiro vetor a 1, e o final está no final do último vetor a n, uma linha quebrada composta de uma sequência de somas de vetores Esta regra de adição é chamada de regra de fechamento da linha quebrada No caso a soma de dois vetores é equivalente à regra do paralelogramo.

A linha reta e com direção dada, considerada positiva, é chamada de eixo e.

Uma combinação linear de vetores a i é um vetor a, definido pela fórmula , onde estão alguns números.

Se para um sistema de n vetores a i a igualdade

é verdadeiro apenas se este sistema for considerado linearmente independente. Se a igualdade (1) for satisfeita para , pelo menos um dos quais é diferente de zero, então o sistema de vetores ai é denominado linearmente dependente. Por exemplo, quaisquer vetores colineares, três vetores coplanares, quatro ou mais vetores no espaço tridimensional são sempre linearmente dependentes.

Três vetores linearmente independentes ordenados ē 1, ē 2, ē 3 no espaço são chamados de base. Um triplo ordenado de vetores não coplanares sempre forma uma base. Qualquer vetor a no espaço pode ser expandido de acordo com a base ē 1, ē 2, ē 3, ou seja, representar a como uma combinação linear de vetores de base: uma= xē 1 + yē 2 + zē 3, onde x, y, z são o vetor de coordenadas a na base ē 1, ē 2, ē 3. Uma base é chamada ortonormal se seus vetores são perpendiculares entre si e têm comprimento unitário. Tal base é denotada por i, j, k, ou seja, i=(1, 0, 0), j=(0, 1, 0), k=(0, 0, 1).

Exemplo 5. Os vetores são especificados em uma base ortonormal i, j, k por coordenadas: a=(2;-1;8), e 1 = (1,2,3), e 2 = (1,-1,- 2), e 3 = (1,-6,0). Certifique-se de que o triplo e 1, e 2, e 3 forma uma base e encontre as coordenadas do vetor nesta base.

Solução. Se o determinante , composto pelas coordenadas dos vetores e 1, e 2, e 3, não é igual a 0, então os vetores e 1, e 2, e 3 são linearmente independentes e, portanto, formam uma base. Garantimos que = -18-4+3-12=-31 Assim, o triplo e 1, e 2, e 3 é a base.

Vamos denotar as coordenadas do vetor a na base e 1 , e 2 , e 3 por x, y, z. Então a = (x,y,z) = xe 1 + yе 2 + zе 3. Visto que pela condição a = 2i – j +8k, e 1 = i +2j +3k, e 2 = i – j -2k, e 3 = i – 6j, então da igualdade a = xe1 + ye 2 + zе 3 isto Segue-se que 2i – j +8k = xi + 2xj + 3xk + yi – yj -2yk +zi -6zj = (x+y+z)i +(2x-y-6z)j +(3x-2y)k. . Como você pode ver, o vetor do lado esquerdo da igualdade resultante é igual ao vetor do lado direito, e isso só é possível se suas coordenadas correspondentes forem iguais. A partir daqui obtemos um sistema para encontrar as incógnitas x, y, z:

Sua solução: x = 2, y = -1, z = 1. Então, a = 2e 1 – e 2 + e 3 = (2,-1,1).

Decomposição vetorial. Produto escalar de vetores.

Produto escalarÀs vezes produto Interno- cirurgia em dois vetores, cujo resultado é o número ( escalar), independente do sistema de coordenadas e caracterizando os comprimentos dos vetores fatoriais e o ângulo entre eles. Esta operação corresponde à multiplicação comprimento vetor x ligado projeção vetor y para vetor x. Esta operação é geralmente considerada como comutativo E linear para cada fator.

Normalmente, uma das seguintes notações é usada:

ou ( designação Dirac, frequentemente usado em mecânica quântica para vetores de estado):

Geralmente é assumido que o produto escalar é positivo definido, isto é

Para todos .

Se isso não for assumido, então o trabalho é chamado indeterminado.

Produto escalar V Espaço vetorial acima campo complexo(ou real) númerosé uma função para elementos que assumem valores em (ou), definida para cada par de elementos e satisfazendo as seguintes condições:

Note-se que do parágrafo 2 da definição segue-se que . Portanto, o item 3 faz sentido, apesar dos valores complexos (no caso geral) produto escalar.

Produto vetorial de vetores.

Arte vetorial- Esse pseudovetor, perpendicular plano construído a partir de dois fatores, que é o resultado operação binária"multiplicação de vetores" acabou vetores em três dimensões Espaço euclidiano. O trabalho não é nem comutativo, nenhum associativo(isso é anticomutativo) e difere de produto escalar de vetores. Em muitos problemas de engenharia e física, você precisa ser capaz de construir um vetor perpendicular a dois existentes - o produto vetorial oferece essa oportunidade. O produto vetorial é útil para "medir" a perpendicularidade dos vetores - o comprimento do produto vetorial de dois vetores é igual ao produto de seus comprimentos se eles forem perpendiculares e diminui para zero se os vetores forem paralelos ou antiparalelos.

O produto vetorial pode ser definido de diferentes maneiras e, teoricamente, em um espaço de qualquer dimensão n você pode calcular o produto n-1 vetores, obtendo um único vetor perpendicular a todos eles. Mas se o produto for limitado a produtos binários não triviais com resultados vetoriais, então o produto vetorial tradicional é definido apenas em três dimensões e sete dimensões espaços. Resultado produto vetorial, como o escalar, depende de Métricas Espaço euclidiano.

Ao contrário da fórmula para calcular a partir de coordenadas vetoriais produto escalar em três dimensões sistema de coordenadas retangulares, a fórmula para o produto vetorial depende de orientação sistema de coordenadas retangulares ou, em outras palavras, seu “ quiralidade».

Produto misto de vetores

Produto misto vetores - produto escalar vetor sobre produto vetorial vetores E :

Às vezes é chamado produto escalar triplo vetores, aparentemente devido ao fato de que o resultado é escalar(mais precisamente - pseudoescalar).

Significado geométrico: O módulo do produto misto é numericamente igual ao volume paralelepípedo, educado vetores .

Trabalho misto assimétrico em relação a todos os seus argumentos:

isto é, reorganizar quaisquer dois fatores altera o sinal do produto. Segue que

Em particular,

Um trabalho misto pode ser convenientemente escrito usando Símbolo Levi-Civita (tensor):

(na última fórmula em uma base ortonormal, todos os índices podem ser escritos como inferiores; neste caso, esta fórmula repete de forma totalmente direta a fórmula com o determinante, porém, neste caso um multiplicador (-1) é obtido automaticamente para o bases esquerdas).

Sistema de coordenadas retangulares cartesianas em um plano.

Tomemos duas retas mutuamente perpendiculares no plano - dois eixos coordenados Ox e Oy com as direções positivas indicadas neles (Fig. 1). As retas Ox e Oy são chamadas de eixos coordenados, o ponto de sua intersecção O é a origem das coordenadas.

Os eixos coordenados Ox, Oy com a unidade de escala selecionada são chamados de sistema de coordenadas cartesianas retangulares (ou retangulares) no plano.

Atribuamos dois números a um ponto arbitrário M do plano: a abscissa x, igual à distância do ponto M ao eixo Oy, tomada com o sinal “+” se M estiver à direita de Oy, e com o Sinal “-” se M estiver à esquerda de Oy; ordenada y, igual à distância do ponto M ao eixo do Boi, tomada com o sinal “+” se M estiver acima de Ox, e com o sinal “-” se M estiver abaixo de Ox. A abscissa x e a ordenada y são chamadas de coordenadas retangulares cartesianas do ponto M(x;y).

A origem possui coordenadas (0;0). Os eixos coordenados dividem o plano em quatro partes chamadas quartos ou quadrantes (às vezes também chamados de ângulos coordenados). A parte do plano delimitada entre os semieixos positivos Ox e Oy é chamada de primeiro quadrante. A seguir, os quadrantes são numerados no sentido anti-horário (Fig. 2). Para todos os pontos do primeiro quadrante x>0, y>0; para pontos I do quadrante x<0, у>0, no quadrante I I I x<0, у<0 и в IV квадранте х>0, sim<0.

Coordenadas polares.

Sistema de coordenadas polares- um sistema de coordenadas bidimensional em que cada ponto do plano é definido por dois números - o ângulo polar e o raio polar. O sistema de coordenadas polares é especialmente útil nos casos em que as relações entre pontos são mais facilmente representadas em termos de raios e ângulos; no mais comum cartesiano ou sistema de coordenadas retangular, tais relações só podem ser estabelecidas aplicando trigonométrico equações.

O sistema de coordenadas polares é definido por um raio, chamado eixo zero ou eixo polar. O ponto de onde emerge este raio é chamado origem ou pólo. Qualquer ponto do plano é definido por duas coordenadas polares: radial e angular. A coordenada radial (geralmente denotada por ) corresponde à distância de um ponto à origem. Coordenada angular, também chamada de ângulo polar ou azimute e é denotado como , é igual ao ângulo pelo qual o eixo polar deve ser girado no sentido anti-horário para chegar a este ponto.

A coordenada radial assim definida pode assumir valores de zero antes infinidade, e a coordenada angular varia de 0° a 360°. No entanto, por conveniência, a faixa de valores da coordenada polar pode ser expandida além

Equação de uma linha reta em um plano

Machado + Wu + C = 0,

Além disso, as constantes A e B não são iguais a zero ao mesmo tempo. Esta equação de primeira ordem é chamada equação geral de uma reta. Dependendo dos valores das constantes A, B e C, são possíveis os seguintes casos especiais:

C = 0, A ≠0, B ≠ 0 – a reta passa pela origem

A = 0, B ≠0, C ≠0 (By + C = 0) - reta paralela ao eixo do Boi

B = 0, A ≠0, C ≠ 0 (Ax + C = 0) – reta paralela ao eixo Oy

B = C = 0, A ≠0 – a reta coincide com o eixo Oy

A = C = 0, B ≠0 – a reta coincide com o eixo do Boi

A equação de uma linha reta pode ser apresentada de diferentes formas, dependendo de quaisquer condições iniciais.

As principais tarefas de usar a equação de uma reta

Não posso responder

Curvas de segunda ordem

Curva de segunda ordem- lugar geométrico de pontos cujas coordenadas retangulares cartesianas satisfazem uma equação da forma

em que pelo menos um dos coeficientes é diferente de zero.

Limite de sequência numérica e função

Limite da sequência numérica. Considere uma sequência numérica cujo termo comum se aproxima de algum número a aumentando o número de série n. Neste caso, diz-se que a sequência numérica tem limite. Este conceito tem uma definição mais estrita.

Esta definição significa que a Há limite sequência numérica se seu termo comum se aproxima sem limite a com o aumento n. Geometricamente, isso significa que para qualquer > 0 pode-se encontrar tal número N que a partir de n > N todos membros da sequência estão localizados dentro do intervalo ( a a). Uma sequência que tem um limite é chamada convergente; de outra forma - divergente.

A sequência é chamada limitado, se tal número existir M o que | você n | M  para todos n . Uma sequência crescente ou decrescente é chamada monótono.

Teoremas básicos sobre limites e suas aplicações

Teorema 1 . (sobre a passagem ao limite na igualdade) Se duas funções assumem os mesmos valores nas proximidades de um determinado ponto, então seus limites neste ponto coincidem.

Teorema 2. (sobre a passagem ao limite da desigualdade) Se os valores da função f(x) na vizinhança de um determinado ponto não exceda os valores correspondentes da função g(x) , então o limite da função f(x) neste ponto não excede o limite da função g(x) .

Teorema 3 . O limite de uma constante é igual à própria constante.

Prova. f(x)=c, vamos provar isso.

Vamos pegar um >0 arbitrário. Como  você pode pegar qualquer

número positivo. Então em

Teorema 4. Função não pode haver dois limites diferentes em

um ponto.

Prova. Vamos supor o contrário. Deixar

E .

Por o teorema sobre a conexão entre o limite e a função infinitesimal:

f(x)- A= - b.m. no ,

f(x)- B= - b.m. no .

Subtraindo essas igualdades, obtemos:

B-A= - .

Passando aos limites de ambos os lados da igualdade em , temos:

B-A=0, ou seja B=A. Obtemos uma contradição que prova o teorema.

Teorema 5. Se cada termo de uma soma algébrica de funções tem um limite em, então a soma algébrica também tem um limite em, e o limite da soma algébrica é igual à soma algébrica dos limites.

.

Prova. Deixar , , .

Então, por teorema sobre a conexão entre o limite e b.m. funções:

Onde - b.m. no .

Vamos adicionar essas igualdades algebricamente:

f(x)+ g(x)- h(x)-(A+B-C)= ,

Onde b.m. no .

De acordo com o teorema sobre a conexão entre o limite e b.m. Características:

A+B-C= .

Teorema 6. Se cada um dos fatores de um produto de um número finito de funções tem um limite em, então o produto também tem um limite em, e o limite do produto é igual ao produto dos limites.

.

Consequência. O fator constante pode ser levado além do sinal limite.

.

Teorema 7. Se as funções f(x) E g(x) tem um limite em ,

e, então o quociente deles também tem um limite em, e o limite do quociente é igual ao quociente dos limites.

, .

Continuidade de função

Na Fig. 15, e o gráfico da função é mostrado . É natural chamá-lo de gráfico contínuo porque pode ser desenhado com um movimento de lápis sem levantá-lo do papel. Vamos definir um ponto arbitrário (número). Outro ponto próximo a ele pode ser escrito na forma , onde existe um número positivo ou negativo denominado incremento. Diferença

é chamado de incremento da função no ponto correspondente ao incremento. O que se quer dizer aqui é que . Na Fig. 15, e é igual ao comprimento do segmento.

Nós nos esforçaremos para chegar a zero; então, para a função em questão, obviamente tenderá a zero:

. (1)

Consideremos agora o gráfico da Fig. 15, b. Consiste em duas peças contínuas e. No entanto, essas peças não estão continuamente conectadas e, portanto, é natural chamar o gráfico de descontínuo. Para que o gráfico represente uma função de valor único no ponto , vamos concordar que é igual ao comprimento do segmento que conecta e ; como sinal disso, o ponto é representado no gráfico com um círculo, enquanto o ponto tem uma seta desenhada, indicando que não pertence ao gráfico. Se o ponto pertencesse ao gráfico, então a função teria dois valores no ponto.

Vamos agora adicionar um incremento e determinar o incremento correspondente da função:

Se tendermos a zero, agora não será mais possível dizer o que tenderá a zero. Para os negativos tendendo a zero, isso é verdade, mas para os positivos não é o caso: pela figura fica claro que se, embora permaneça positivo, tende a zero, então o incremento correspondente tende a um número positivo igual ao comprimento do segmento.

Após essas considerações, é natural chamar uma função definida em um intervalo contínuo em um ponto deste segmento se seu incremento neste ponto, correspondente ao incremento, tende a zero de qualquer forma que tende a zero. Esta (a propriedade da continuidade em) é escrita na forma da relação (1) ou também assim:

A entrada (2) é assim: o limite é igual a zero quando tende a zero de acordo com qualquer lei. Porém, a expressão “conforme qualquer lei” costuma ser omitida, implicando-a.

Se uma função definida em não for contínua no ponto, isto é, se a propriedade (2) não for válida para ela em pelo menos uma maneira de tender a zero, então ela é chamada de descontínua no ponto.

A função mostrada na Fig. 15, a, é contínua em qualquer ponto, mas a função mostrada na Fig. 15, b, obviamente, é contínuo em qualquer ponto, com exceção do ponto, pois para este último, a relação (2) não é satisfeita quando, permanecendo positiva.

Uma função que é contínua em qualquer ponto de um segmento (intervalo) é chamada contínua nesse segmento (intervalo).

Uma função contínua expressa matematicamente uma propriedade que frequentemente encontramos na prática, nomeadamente que um pequeno incremento numa variável independente corresponde a um pequeno incremento numa variável dependente (função). Excelentes exemplos de função contínua são várias leis do movimento dos corpos, expressando a dependência do caminho percorrido pelo corpo em relação ao tempo. O tempo e o espaço são contínuos. Esta ou aquela lei do movimento estabelece uma certa ligação contínua entre eles, caracterizada pelo fato de que um pequeno incremento de tempo corresponde a um pequeno incremento de caminho.

O homem chegou à abstração da continuidade observando os chamados meios contínuos ao seu redor - sólido, líquido ou gasoso, por exemplo metais, água, ar. Na verdade, qualquer meio físico é um acúmulo de um grande número de partículas em movimento separadas umas das outras. No entanto, essas partículas e as distâncias entre elas são tão pequenas em comparação com os volumes de meio com que se tem de lidar nos fenômenos físicos macroscópicos que muitos desses fenômenos podem ser estudados muito bem se considerarmos aproximadamente a massa do meio em estudo como sendo distribuído continuamente sem lacunas no espaço por ele ocupado. Muitas disciplinas físicas são baseadas nesta suposição, por exemplo, hidrodinâmica, aerodinâmica e teoria da elasticidade. O conceito matemático de continuidade desempenha naturalmente um papel importante nestas disciplinas, como em muitas outras.

As funções contínuas formam a principal classe de funções com as quais opera a análise matemática.

Exemplos de funções contínuas são funções elementares (ver § 3.8 abaixo). Eles são contínuos ao longo dos intervalos de mudança onde são definidos.

Funções descontínuas em matemática refletem processos descontínuos encontrados na natureza. Durante um impacto, por exemplo, a velocidade de um corpo muda abruptamente. Muitas transições de qualidade são acompanhadas de saltos. Por exemplo, a relação entre a temperatura de um grama de água (gelo) e a quantidade de calorias de calor nela contidas, quando varia entre e , se assumirmos convencionalmente que no valor de , é expressa pelas seguintes fórmulas:

Assumimos que a capacidade térmica do gelo é 0,5. Quando esta função acaba sendo indefinida – com vários valores; Por conveniência, podemos concordar que at assume um valor bem definido, por exemplo. A função, obviamente descontínua em , é mostrada na Fig. 16.

Vamos definir a continuidade de uma função em um ponto.

Uma função é chamada contínua em um ponto se for definida em alguma vizinhança deste ponto, inclusive no próprio ponto, e se seu incremento neste ponto, correspondente ao incremento do argumento, tende a zero em:

Se colocarmos , obtemos a seguinte definição equivalente de continuidade em: uma função é contínua em um ponto se for definida em alguma vizinhança deste ponto, inclusive no próprio ponto, e se

; (4)

ou também na língua: se para todos existe tal que

A igualdade (4) também pode ser escrita da seguinte forma:

. (4’)

Mostra que sob o signo de uma função contínua pode-se ir até o limite.

Exemplo 1. Uma constante é uma função contínua em qualquer ponto. Na verdade, um ponto corresponde ao valor de uma função, um ponto corresponde ao mesmo valor . É por isso

.

EXEMPLO 2. A função é contínua para qualquer valor porque e, portanto, para .

Exemplo 3. A função é contínua para qualquer. De fato,

Mas para todos existe desigualdade

Se , então isso segue da Fig. 17, que mostra um círculo de raio 1 (o arco de comprimento é maior que a corda por ele subtendida, que tem comprimento ). Quando a desigualdade (6) se transforma em igualdade. Se então . Finalmente, se , então . De (5) baseado em (6) segue

,

Mas então obviamente

Também podemos dizer que para todos é possível encontrar exatamente tal que

Observemos um teorema importante.

Teorema 1. Se as funções e são contínuas em um ponto, então sua soma, diferença, produto e quociente (at) também são contínuas neste ponto.

Este teorema segue diretamente do Teorema 6 §3.2, levando em consideração que neste caso

Um importante teorema sobre a continuidade de uma função a partir de uma função (função complexa) também é verdadeiro.

Teorema 2. Seja dada uma função que seja contínua no ponto e outra função que seja contínua no ponto e seja. Então a função complexa é contínuo no ponto.

Prova. Observe que pela definição de continuidade de uma função em um ponto segue-se que ela está definida em alguma vizinhança deste ponto. É por isso

Aqui uma substituição é introduzida e a continuidade no ponto é levada em consideração .

Exemplo 4. Função

onde estão os coeficientes constantes, é chamado de polinômio de grau. É contínuo para qualquer um. Afinal, para obter é necessário, com base em números constantes e na função, realizar um número finito de operações aritméticas - adição, subtração e multiplicação. Mas uma constante é uma função contínua (ver exemplo 1), e uma função também é contínua (ver exemplo 2), então a continuidade segue do Teorema 1.

Exemplo 5. A função é contínua. É uma composição de duas funções contínuas: , .

Exemplo 6. Função

é contínuo para o especificado, porque (ver Teorema 1) é igual ao quociente da divisão de funções contínuas e o divisor não é igual a zero (para o especificado).

Exemplo 7. Função

é contínuo para qualquer, porque é uma composição de funções contínuas:,, (ver Teorema 2).

Exemplo 8. A função é contínua porque

Exemplo 9. Se uma função é contínua num ponto, então a função também é contínua neste ponto.

Isto segue do Teorema 2 e do Exemplo 8, porque uma função é uma composição de duas funções contínuas,.

Observemos mais dois teoremas que decorrem diretamente dos Teoremas 1 e 2 correspondentes de §3.2 para o limite de uma função.

Teorema 3. Se uma função é contínua em um ponto, então existe uma vizinhança desse ponto na qual ela é limitada.

Teorema 4. Se a função é contínua no ponto e , então existe uma vizinhança do ponto em que

.

Além disso, se , então

e se, então

O conceito de derivada.

Derivado(funções em um ponto) - conceito básico cálculo diferencial, caracterizando a taxa de variação da função (em um determinado ponto). Definido como limite a relação entre o incremento de uma função e seu incremento argumento quando o incremento do argumento tende a zero, se tal limite existir. Uma função que possui uma derivada finita (em algum ponto) é chamada diferenciável (nesse ponto).

O processo de cálculo da derivada é chamado diferenciação. Processo reverso - descoberta antiderivada - integração.

Significado geométrico e mecânico das derivadas.

Regras de diferenciação.

Derivada de uma soma algébrica de funções

Teorema 1. Derivado a soma (diferença) de duas funções diferenciáveis ​​​​é igual à soma (diferença) das derivadas dessas funções:

(você±v)" = você"±v"

Consequência. A derivada de uma soma algébrica finita de funções diferenciáveis ​​​​é igual à mesma soma algébrica de derivadas de termos. Por exemplo,

(você - v + w)" = você" - v" + w"

A derivada do produto de funções é determinada por

Teorema 2. A derivada do produto de duas funções diferenciáveis ​​​​é igual ao produto da primeira função e a derivada da segunda mais o produto da segunda função e a derivada da primeira, ou seja,

(uv)" = você"v + uv"

Corolário 1. O fator constante pode ser retirado do sinal da derivada (cv)" = cv" (c = const).

Corolário 2. A derivada do produto de várias funções diferenciáveis ​​é igual à soma dos produtos da derivada de cada uma delas por todas as outras.

Por exemplo, (uvw)" = u"vw + uv"w + uvw"

Derivada do quociente de duas funções

é expresso pelo seguinte teorema.

Teorema 3. A derivada do quociente de duas funções diferenciáveis ​​é determinada pela fórmula

A derivada de uma função complexa é expressa por

Teorema 4. Se y = f(u) e u = (ф(x)) são funções diferenciáveis ​​de seus argumentos, então derivada de uma função complexa y = f (ф(x)) existe e é igual ao produto da derivada desta função em relação ao argumento intermediário e a derivada do argumento intermediário em relação à variável independente, ou seja,

Muitas vezes em testes em matemática em derivadas funções complexas são fornecidas, por exemplo, y = sin(cos5x). A derivada de tal função é igual a -5sin5x*sin(cos5x)

Veja um exemplo de cálculo de uma função complexa no vídeo a seguir

Derivadas de funções elementares.

Ao resolver problemas de diferenciação, é preciso procurar derivadas de funções várias aulas. Neste artigo veremos os principais regras de diferenciação, que usaremos constantemente ao encontrar derivadas. Provaremos todas essas regras com base na definição da derivada de uma função e definitivamente nos concentraremos em solução detalhada exemplos para compreender o princípio de sua aplicação.

Ao provar as regras de diferenciação, assumiremos que as funções f(x) e g(x) são diferenciáveis ​​em algum intervalo X.

Ou seja, para qualquer um é verdade que , onde estão os incrementos das funções correspondentes.

Em outra postagem.

As regras básicas de diferenciação incluem:

Realizando um fator constante além do sinal da derivada.

Vamos provar a fórmula. Pela definição de derivada temos:

Um fator arbitrário pode ser levado além do sinal de passagem ao limite (isso é conhecido pelas propriedades do limite), portanto

Isto completa a prova da primeira regra de diferenciação.

Muitas vezes é necessário primeiro simplificar a forma da função diferenciável para usar a tabela de derivadas e as regras para encontrar derivadas. Os exemplos a seguir confirmam isso claramente.

Exemplo.

Execute a diferenciação de funções .

Solução.

Com base nas propriedades da função logarítmica, você pode passar para a notação. Resta lembrar a derivada da função logarítmica e adicionar um fator constante:

Exemplo.

Solução.

Vamos transformar a função original .

Aplicamos a regra de colocar o multiplicador fora do sinal da derivada e retiramos a derivada da função exponencial da tabela:

Derivada de uma soma, derivada de uma diferença.

Para provar a segunda regra de diferenciação, usamos a definição de derivada e a propriedade do limite de uma função contínua.

De forma semelhante, pode-se provar que a derivada da soma (diferença) de n funções é igual à soma (diferença) de n derivadas.

Exemplo.

Encontre a derivada de uma função .

Solução.

Vamos simplificar a forma da função original.

Usamos a regra da soma derivada (diferença):

No parágrafo anterior provamos que o fator constante pode ser retirado do sinal da derivada, portanto

Resta apenas usar a tabela de derivadas:

Derivada do produto de funções.

Vamos provar a regra para diferenciar o produto de duas funções.

Vamos anotar o limite da razão entre o incremento de um produto de funções e o incremento do argumento. Levaremos em conta que e (o incremento da função tende a zero assim como o incremento do argumento tende a zero).

Q.E.D.

Exemplo.

Função diferenciada .

Solução.

EM neste exemplo. Aplicamos a regra da derivada do produto:

Voltamo-nos para a tabela de derivadas de funções elementares básicas e obtemos a resposta:

Exemplo.

Encontre a derivada da função.

Solução.

Neste exemplo . Por isso,

Vejamos o caso de encontrar a derivada do produto de três funções. Em princípio, utilizando o mesmo sistema é possível diferenciar o produto de quatro, cinco e vinte e cinco funções.

Exemplo.

Execute a diferenciação da função.

Solução.

Partiremos da regra de diferenciação do produto de duas funções. Como função f(x) consideraremos o produto (1+x)sinx, e como g(x) consideraremos lnx:

Encontrar Aplicamos novamente a regra da derivada do produto:

Usamos a regra da soma das derivadas e a tabela de derivadas:

Vamos substituir o resultado:

Como você pode ver, às vezes é necessário aplicar várias regras de diferenciação em um exemplo. Não há nada de complicado nisso, o principal é agir de forma consistente e não misturar tudo.

Exemplo.

Encontre a derivada da função.

Solução.

A função representa a diferença das expressões e, portanto

Na primeira expressão retiramos os dois do sinal de derivada, e na segunda expressão aplicamos a regra de diferenciação do produto:

Derivada do quociente de duas funções (derivada de uma fração).

Vamos provar a regra para diferenciar o quociente de duas funções (frações) . Vale ressaltar que g(x) não desaparece para nenhum x no intervalo X.

ções, devido às quais a igualdade (3.10) desempenha um papel importante tanto nos estudos teóricos quanto nos cálculos aproximados.

As operações para encontrar a derivada e a diferencial de uma função são chamadas diferenciação esta função. Nome comum ambas as operações são explicadas pela sua óbvia dependência. Em virtude da fórmula (3.8), o diferencial de uma função é obtido simplesmente multiplicando seu produto

erros de portadora que surgem ao substituir o incremento de uma função pelo seu diferencial.

Vamos encontrar o incremento e o diferencial da função

y = 3(x+ x) 2 + (x+ x) − 3 x2 − x= 6 x x+ 3(x) 2 + x= (6 x+ 1) x+ (x) 2 .

Então dy = (6 x + 1) x. Vamos calcular udy no ponto x = 1 se x = 0, 1 y = 7 0, 1 + 3 0, 01 = 0, 73; dy = 7 0 , 1 = 0 , 7 .

O erro absoluto é y - dy = 0,73 - 0,7 = 0,03, e o erro relativo

y = 0 0 , , 03 73 ≈0 ,04 .

3.5. Derivada de soma, produto e quociente de funções

Vamos relembrar os famosos do curso ensino médio regras de diferenciação, que permitem em alguns casos encontrar derivadas de funções sem recorrer diretamente à definição.

Teorema 3.3. Se as funções u = u (x) e v = v (x)

diferenciável

Multiplicando o termo dessas igualdades por dx, obtemos as mesmas regras escritas em termos de diferenciais

Prova. Como a prova para todas as partes do teorema é realizada de maneira completamente uniforme, provaremos uma delas, por exemplo, a segunda.

Vamos denotar y = uv. Vamos dar x incremento x e deixar

referenciável e, portanto, contínuo (Teorema 3.2), portanto

O tel pode ser retirado dos sinais derivativos e diferenciais.

Para o caso de três fatores, aplicando sucessivamente a fórmula

(3.12), encontramos

(uvw) ′ = ((uv) w) ′ = (uv) ′ w+ (uv) w′+ (u′ v+ uv′ ) w+ uvw′ = = u ′ vw + uv ′ w + uvw ′.

Uma regra semelhante é válida ao diferenciar o produto de qualquer número de fatores.

Nos parágrafos seguintes serão obtidas derivadas das principais funções elementares.

3.6. Derivadas de funções trigonométricas

Vamos encontrar as derivadas de funções trigonométricas, a saber

Vamos pegar o primeiro. Incremento da função y = sin x no ponto x, co-

A segunda fórmula é comprovada de maneira semelhante. A terceira e quarta fórmulas são obtidas se a tangente e a cotangente forem expressas em termos de seno e cosseno e usarem a fórmula (3.13).

3.7. Diferenciando funções logarítmicas

Vamos provar o primeiro deles. Incremento da função y = log a x no ponto x, co-

(usamos aqui o log de identidade a A = log a e ln A ).

3.8. Diferenciação de uma função complexa.

Derivadas de potência e funções exponenciais

Seja uma função complexa y argumentosx dada pelas fórmulas y = f (u),

u = ϕ (x) (ver parágrafo 1.4.3)

Teorema 3.4 (sobre a derivada de uma função complexa). Se as funções

incremento y da função y = f (u) . Como a função y = f (u) de acordo com as condições do teorema é diferenciável no ponto u em consideração, então seu incremento neste ponto pode ser representado na forma (ver Definição 3.4)

x → 0, chegamos a (3.18).

Multiplicando a igualdade (3.18) termo a termo por dx, obtemos uma expressão para o diferencial de uma função complexa

dy = f′ (u) du.

Comente. A diferencial da função y = f (u) teria exatamente a mesma forma se o argumento u não fosse uma função, mas uma variável independente. Isto é o que é chamado propriedade de invariância(independência) da forma do diferencial em relação ao argumento. Deve-se ter em mente que se u é uma variável independente, então du = u é seu incremento arbitrário, se u é um argumento intermediário (ou seja, uma função), então du é o diferencial desta função, ou seja, um valor que não coincide com seu incremento u.

Usando o último teorema, é fácil obter fórmulas de diferenciação

o lado esquerdo da última igualdade é uma função complexa de x. Diferenciando ambos os lados da última igualdade em relação a x (o lado esquerdo como uma função complexa), obtemos

1 y y ′ =uma 1 x ,

y ′ =ay x =ax x a =ax a − 1 .

É fácil mostrar que este resultado também é verdadeiro para x< 0 , если только при

neste caso x α faz sentido. Anteriormente, o resultado era obtido para o caso α = n. A segunda fórmula é obtida de forma semelhante, da qual, no caso especial de a = e, segue a última fórmula.

Comente. A técnica do logaritmo preliminar, que foi utilizada para obter a fórmula de diferenciação de uma função de potência, tem significado independente e é chamada em conjunto com a posterior descoberta da derivada do logaritmo da função

lnx ) "= cosx lnx + sin x x .

Por isso,

y ′ = x sen x (cosx lnx + sen x x)

Comente. A regra para diferenciar uma função complexa também pode ser aplicada para encontrar a derivada de uma função especificada implicitamente.

Na verdade, se a relação entre x e y for dada na forma F (x, y) = 0 e esta equação for solucionável em relação a y, então a derivada y ′ pode ser encontrada a partir da equação

3.9. Diferenciação de uma função inversa.

Diferenciação de funções trigonométricas inversas

Deixe dois serem dados mutuamente funções inversas y = f (x) e x = ϕ (y)

(ver cláusula 1.4.8).

Teorema 3.5 (sobre a derivada da função inversa). Se as funções