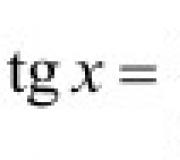Trygonometria jest prosta i jasna. Trygonometria Wyjaśnienie funkcji trygonometrycznych

Wykonując konwersje trygonometryczne, postępuj zgodnie z poniższymi wskazówkami:

1. Nie próbuj od razu wymyślać rozwiązania przykładu od początku do końca.
2. Nie próbuj konwertować całego przykładu na raz. Rób małe kroki do przodu.
3. Pamiętaj, że oprócz wzorów trygonometrycznych w trygonometrii nadal możesz używać wszystkich sprawiedliwych przekształceń algebraicznych (nawiasy, skracanie ułamków, skrócone wzory na mnożenie i tak dalej).
4. Uwierz, że wszystko będzie dobrze.

Podstawowe wzory trygonometryczne

Większość wzorów w trygonometrii jest często używana zarówno od prawej do lewej, jak i od lewej do prawej, dlatego musisz nauczyć się tych wzorów na tyle dobrze, aby móc łatwo zastosować pewne wzory w obu kierunkach. Zapiszmy najpierw definicje funkcji trygonometrycznych. Niech będzie trójkąt prostokątny:

Następnie definicja sinusa:

Definicja cosinusa:

Definicja stycznej:

Definicja kotangensu:

Podstawowa tożsamość trygonometryczna:

Najprostsze wnioski z podstawowej tożsamości trygonometrycznej:

Wzory na kąt podwójny. Sinus podwójnego kąta:

Cosinus podwójnego kąta:

Tangens kąta podwójnego:

Cotangens kąta podwójnego:

Dodatkowe wzory trygonometryczne

Wzory na dodawanie trygonometryczne. Sinus sumy:

Sinus różnicy:

Cosinus sumy:

Cosinus różnicy:

Tangens sumy:

Tangens różnicy:

Cotangens ilości:

Kotangens różnicy:

Wzory trygonometryczne do przeliczania sumy na iloczyn. Suma sinusów:

Różnica sinusowa:

Suma cosinusów:

Różnica cosinusów:

Suma tangensów:

Różnica styczna:

Suma kotangentów:

Różnica cotangensowa:

Wzory trygonometryczne służące do przeliczania iloczynu na sumę. Iloczyn sinusów:

Iloczyn sinusa i cosinusa:

Iloczyn cosinusów:

Wzory na redukcję stopni.

Wzory na półkąta.

Trygonometryczne wzory redukcyjne

Nazywa się funkcję cosinus współfunkcja funkcje sinusowe i odwrotnie. Podobnie funkcje tangens i cotangens są kofunkcjami. Wzory redukcyjne można sformułować w postaci następującej reguły:

• Jeśli we wzorze redukcyjnym odejmie się (doda) kąt od 90 stopni lub 270 stopni, wówczas funkcja zredukowana zamienia się w kofunkcję;
• Jeżeli we wzorze redukcji kąt zostanie odjęty (dodany) od 180 stopni lub 360 stopni, wówczas nazwa funkcji zredukowanej zostaje zachowana;
• W tym przypadku znak, który funkcja zredukowana (tj. pierwotna) ma w odpowiedniej ćwiartce, umieszcza się przed funkcją zredukowaną, jeśli kąt odjęty (dodany) uznamy za ostry.

Formuły redukcyjne podano w formie tabelarycznej:

Przez okrąg trygonometrycznyłatwe do określenia wartości tabelaryczne funkcji trygonometrycznych:

Równania trygonometryczne

Aby rozwiązać pewne równanie trygonometryczne, należy je sprowadzić do jednego z najprostszych równań trygonometrycznych, które zostaną omówione poniżej. Dla tego:

• Możesz skorzystać ze wzorów trygonometrycznych podanych powyżej. Jednocześnie nie musisz od razu próbować przekształcać całego przykładu, ale musisz iść do przodu małymi krokami.
• Nie można zapominać o możliwości przekształcenia jakiegoś wyrażenia metodami algebraicznymi, tj. na przykład wyjmij coś z nawiasów lub odwrotnie, otwórz nawiasy, zmniejsz ułamek, zastosuj skróconą formułę mnożenia, sprowadź ułamki do wspólnego mianownika i tak dalej.
• Rozwiązując równania trygonometryczne, możesz użyć metoda grupowania. Należy pamiętać, że aby iloczyn kilku czynników był równy zero, wystarczy, że którykolwiek z nich będzie równy zero, a reszta istniała.
• Stosowanie metoda zastępowania zmiennych, jak zwykle, równanie po wprowadzeniu zamiany powinno stać się prostsze i nie zawierać pierwotnej zmiennej. Trzeba także pamiętać o wykonaniu odwrotnej wymiany.
• Pamiętaj, że w trygonometrii często pojawiają się równania jednorodne.
• Otwierając moduły lub rozwiązując irracjonalne równania za pomocą funkcji trygonometrycznych, należy pamiętać i wziąć pod uwagę wszystkie subtelności rozwiązywania odpowiednich równań za pomocą zwykłych funkcji.
• Pamiętaj o ODZ (w równaniach trygonometrycznych ograniczenia ODZ sprowadzają się głównie do tego, że nie można dzielić przez zero, ale nie zapominaj o innych ograniczeniach, zwłaszcza o dodatniości wyrażeń w potęgach wymiernych i pod pierwiastkami potęg parzystych). Pamiętaj też, że wartości sinusa i cosinusa mogą mieścić się tylko w przedziale od minus jeden do plus jeden włącznie.

Najważniejsze jest, jeśli nie wiesz, co robić, zrób przynajmniej coś, a najważniejsze jest prawidłowe użycie wzorów trygonometrycznych. Jeśli to, co otrzymasz, będzie coraz lepsze, kontynuuj rozwiązanie, a jeśli się pogorszy, wróć na początek i spróbuj zastosować inne formuły, rób to, aż znajdziesz właściwe rozwiązanie.

Wzory rozwiązań najprostszych równań trygonometrycznych. Dla sinusa istnieją dwie równoważne formy zapisu rozwiązania:

W przypadku innych funkcji trygonometrycznych zapis jest jednoznaczny. Dla cosinusa:

Dla stycznej:

Dla cotangensu:

Rozwiązywanie równań trygonometrycznych w niektórych szczególnych przypadkach:

Pomyślne, sumienne i odpowiedzialne wdrożenie tych trzech punktów pozwoli Ci pokazać doskonały wynik na CT, maksimum tego, do czego jesteś zdolny.

Znalazłeś błąd?

Jeśli uważasz, że znalazłeś błąd w materiałach szkoleniowych, napisz o tym mailem. Możesz także zgłosić błąd w sieci społecznościowej (). W piśmie podaj temat (fizyka lub matematyka), nazwę lub numer tematu lub testu, numer zadania lub miejsce w tekście (stronie), w którym Twoim zdaniem znajduje się błąd. Opisz również, na czym polega podejrzewany błąd. Twój list nie pozostanie niezauważony, błąd zostanie poprawiony lub zostaniesz wyjaśniony, dlaczego nie jest to błąd.

Zachowanie Twojej prywatności jest dla nas ważne. Z tego powodu opracowaliśmy Politykę prywatności, która opisuje, w jaki sposób wykorzystujemy i przechowujemy Twoje dane. Zapoznaj się z naszymi praktykami dotyczącymi prywatności i daj nam znać, jeśli masz jakiekolwiek pytania.

Gromadzenie i wykorzystywanie danych osobowych

Dane osobowe to dane, które można wykorzystać do identyfikacji konkretnej osoby lub skontaktowania się z nią.

Możesz zostać poproszony o podanie swoich danych osobowych w dowolnym momencie kontaktu z nami.

Poniżej znajduje się kilka przykładów rodzajów danych osobowych, które możemy gromadzić i sposobu, w jaki możemy je wykorzystywać.

Jakie dane osobowe zbieramy:

• Kiedy składasz wniosek na stronie, możemy zbierać różne informacje, w tym Twoje imię i nazwisko, numer telefonu, adres e-mail itp.

Jak wykorzystujemy Twoje dane osobowe:

• Gromadzone przez nas dane osobowe pozwalają nam kontaktować się z Tobą w sprawie wyjątkowych ofert, promocji i innych wydarzeń oraz nadchodzących wydarzeń.
• Od czasu do czasu możemy wykorzystywać Twoje dane osobowe do wysyłania ważnych powiadomień i komunikatów.
• Możemy również wykorzystywać dane osobowe do celów wewnętrznych, takich jak przeprowadzanie audytów, analiza danych i różnych badań w celu ulepszenia świadczonych przez nas usług i przedstawienia rekomendacji dotyczących naszych usług.
• Jeśli bierzesz udział w losowaniu nagród, konkursie lub podobnej promocji, możemy wykorzystać podane przez Ciebie informacje w celu administrowania takimi programami.

Ujawnianie informacji osobom trzecim

Nie udostępniamy otrzymanych od Państwa informacji osobom trzecim.

Wyjątki:

• Jeżeli jest to konieczne – zgodnie z przepisami prawa, procedurą sądową, w postępowaniu sądowym i/lub na podstawie publicznych żądań lub wniosków organów rządowych na terytorium Federacji Rosyjskiej – do ujawnienia Twoich danych osobowych. Możemy również ujawnić informacje o Tobie, jeśli uznamy, że takie ujawnienie jest konieczne lub odpowiednie ze względów bezpieczeństwa, egzekwowania prawa lub innych celów ważnych dla społeczeństwa.
• W przypadku reorganizacji, fuzji lub sprzedaży możemy przekazać zebrane dane osobowe odpowiedniej następczej stronie trzeciej.

Ochrona danych osobowych

Podejmujemy środki ostrożności – w tym administracyjne, techniczne i fizyczne – aby chronić Twoje dane osobowe przed utratą, kradzieżą i niewłaściwym wykorzystaniem, a także nieuprawnionym dostępem, ujawnieniem, zmianą i zniszczeniem.

Szanowanie Twojej prywatności na poziomie firmy

Aby zapewnić bezpieczeństwo Twoich danych osobowych, przekazujemy naszym pracownikom standardy dotyczące prywatności i bezpieczeństwa oraz rygorystycznie egzekwujemy praktyki dotyczące prywatności.

Na tej lekcji poznamy definicje Funkcje trygonometryczne i ich podstawowe własności, naucz się z nimi pracować okrąg trygonometryczny, dowiedzmy się, co to jest okres funkcji i pamiętaj o różnych sposoby mierzenia kątów. Ponadto zrozumiemy użycie formuły redukcyjne.

Ta lekcja pomoże Ci przygotować się do jednego z typów zadań W 7.

Przygotowanie do jednolitego egzaminu państwowego z matematyki

Eksperyment

Lekcja 7.Wprowadzenie do trygonometrii.

Teoria

Podsumowanie lekcji

Dzisiaj rozpoczynamy sekcję, która dla wielu ma przerażającą nazwę „Trygonometria”. Wyjaśnijmy od razu, że nie jest to odrębny przedmiot podobny w nazwie do geometrii, jak niektórzy myślą. Choć przetłumaczone z języka greckiego, słowo „trygonometria” oznacza „pomiar trójkątów” i jest bezpośrednio związane z geometrią. Ponadto obliczenia trygonometryczne są szeroko stosowane w fizyce i technologii. Ale zaczniemy od rozważenia, w jaki sposób podstawowe funkcje trygonometryczne są wprowadzane do geometrii za pomocą trójkąta prostokątnego.

Właśnie użyliśmy terminu „funkcja trygonometryczna” - oznacza to, że wprowadzimy całą klasę pewnych praw zgodności między jedną zmienną a drugą.

Aby to zrobić, rozważ trójkąt prostokątny, w którym dla wygody zastosowano standardowe oznaczenia boków i kątów, co widać na rysunku:

Rozważmy na przykład kąti wprowadź dla niego następujące akcje:

Nazwijmy stosunek strony przeciwnej do sinusa przeciwprostokątnej, tj.

Nazwijmy stosunek sąsiedniej nogi do cosinusa przeciwprostokątnej, tj. ;

Stosunek przeciwnej strony do sąsiedniej strony będzie nazywany styczną, tj. ;

Stosunek sąsiedniego boku do przeciwnego boku będzie nazywany kotangensem, tj. .

Wszystkie te działania pod kątem są wywoływane funkcje trygonometryczne. Sam kąt jest zwykle nazywany argument funkcji trygonometrycznej i można to oznaczyć na przykład przez X, jak to zwykle jest w algebrze.

Ważne jest, aby od razu zrozumieć, że funkcje trygonometryczne zależą w szczególności od kąta w trójkącie prostokątnym, a nie od jego boków. Łatwo to udowodnić, jeśli rozważymy trójkąt podobny do tego, w którym długości boków będą różne, ale wszystkie kąty i stosunki boków nie ulegną zmianie, tj. Funkcje trygonometryczne kątów również pozostaną niezmienione.

Po takiej definicji funkcji trygonometrycznych może pojawić się pytanie: „Czy istnieje np.? W końcu rógnie może znajdować się w trójkącie prostokątnym» . Co dziwne, odpowiedź na to pytanie jest twierdząca, a wartość tego wyrażenia jest równa , co jest jeszcze bardziej zaskakujące, ponieważ wszystkie funkcje trygonometryczne są stosunkiem boków trójkąta prostokątnego, a długości boków wynoszą liczby dodatnie.

Ale nie ma w tym żadnego paradoksu. Faktem jest, że na przykład w fizyce przy opisie niektórych procesów konieczne jest stosowanie funkcji trygonometrycznych kątów nie tylko dużych, ale także dużych i parzystych. W tym celu konieczne jest wprowadzenie bardziej ogólnej zasady obliczania funkcji trygonometrycznych za pomocą tzw „jednostkowy okrąg trygonometryczny”.

Jest to okrąg o promieniu jednostkowym, narysowany tak, że jego środek znajduje się w początku płaszczyzny kartezjańskiej.

Aby przedstawić kąty w tym okręgu, musisz uzgodnić, gdzie je umieścić. Przyjmuje się, że jako promień odniesienia kąta przyjmuje się dodatni kierunek osi odciętych, tj. oś x. Uważa się, że kierunek osadzania się kątów jest przeciwny do ruchu wskazówek zegara. W oparciu o te ustalenia odłóżmy najpierw na bok kąt ostry. To dla takich ostrych kątów wiemy już, jak obliczyć wartości funkcji trygonometrycznych w trójkącie prostokątnym. Okazuje się, że za pomocą przedstawionego koła można również obliczyć funkcje trygonometryczne, tylko wygodniej.

Wartościami sinusa i cosinusa kąta ostrego są współrzędne punktu przecięcia boku tego kąta z okręgiem jednostkowym:

Można to zapisać w ten sposób:

:

Opierając się na fakcie, że współrzędne wzdłuż osi x pokazują wartość cosinusa, a współrzędne wzdłuż osi y pokazują wartość sinusa kąta, wygodnie jest zmienić nazwy osi w układzie współrzędnych za pomocą okręgu jednostkowego, jak widać na rysunku:

Nazwa osi odciętych została zmieniona na oś cosinus, a oś rzędnych na oś sinusoidalną.

Podana zasada wyznaczania sinusa i cosinusa jest uogólniana zarówno na kąty rozwarte, jak i kąty z zakresu od do. W tym przypadku sinusy i cosinusy mogą przyjmować zarówno wartości dodatnie, jak i ujemne. Różny znaki wartości tych funkcji trygonometrycznych w zależności od tego, w której ćwiartce mieści się dany kąt, zwyczajowo przedstawia się go w następujący sposób:

Jak widać, znaki funkcji trygonometrycznych są określone przez dodatnie i ujemne kierunki odpowiednich osi.

Dodatkowo warto zwrócić uwagę na fakt, że skoro największa współrzędna punktu na okręgu jednostkowym zarówno na osi odciętych, jak i na osi rzędnych jest równa jeden, a najmniejsza minus jeden, to wartości sinus i cosinus ograniczone do tych numerów:

Zapisy te są zwykle zapisywane w następującej formie:

Aby wprowadzić funkcje stycznej i cotangensu na okręgu trygonometrycznym, należy narysować dodatkowe elementy: styczną do okręgu w punkcie A – z niej wyznacza się wartość tangensu kąta oraz styczną do okręgu w punkcie A. punkt B - z niego wyznaczana jest wartość cotangensu kąta.

Nie będziemy jednak zagłębiać się w definicję stycznych i cotangensów na okręgu trygonometrycznym, gdyż można je łatwo obliczyć, znając wartości sinusa i cosinusa danego kąta, co już wiemy, jak to zrobić. Jeśli chcesz dowiedzieć się, jak obliczyć tangens i cotangens na okręgu trygonometrycznym, przejrzyj program kursu algebry dla 10. klasy.

Wskazujemy tylko obraz na okręgu znaki stycznych i kotangentów w zależności od kąta:

Należy pamiętać, że podobnie jak w przypadku zakresów wartości sinus i cosinus, można określić zakresy wartości tangensów i cotangensów. Opierając się na ich definicji na okręgu trygonometrycznym, znaczenie tych funkcji nie jest ograniczone:

Co jeszcze można napisać w ten sposób:

Oprócz kątów z zakresu od do, okrąg trygonometryczny umożliwia pracę z większymi kątami, a nawet z kątami ujemnymi. Takie wartości kątów, choć wydają się bez znaczenia dla geometrii, służą do opisu niektórych procesów fizycznych. Na przykład, jak odpowiedzieć na pytanie: „O jaki kąt obróci się wskazówka zegara w ciągu dnia?” W tym czasie wykona dwa pełne obroty, a w jednym obrocie przejdzie, tj. w ciągu jednego dnia zmieni się w . Jak widać, takie wartości mają bardzo praktyczne znaczenie. Znaki kąta służą do wskazania kierunku obrotu - jeden z kierunków przyjmuje się mierzyć kątami dodatnimi, a drugi ujemnymi. Jak można to uwzględnić w okręgu trygonometrycznym?

Na okręgu o takich kątach działają one w następujący sposób:

1) Kąty większe niż , są wykreślane w kierunku przeciwnym do ruchu wskazówek zegara, przechodząc przez początek układu współrzędnych tyle razy, ile jest to konieczne. Na przykład, aby skonstruować kąt, musisz wykonać dwa pełne obroty i kolejny. Wszystkie funkcje trygonometryczne są obliczane dla położenia końcowego. Łatwo zauważyć, że wartości wszystkich funkcji trygonometrycznych for i for będą takie same.

2) Kąty ujemne są układane dokładnie według tej samej zasady, co kąty dodatnie, tylko zgodnie z ruchem wskazówek zegara.

Właśnie metodą konstruowania dużych kątów możemy stwierdzić, że wartości sinusów i cosinusów kątów różniących się są takie same. Jeśli przeanalizujemy wartości stycznych i cotangensów, będą one takie same dla kątów różniących się o .

Takie minimalne liczby niezerowe, dodane do argumentu, nie zmieniają wartości funkcji, nazywane są okres tę funkcję.

Zatem, okressinus i cosinus są równeoraz tangens i cotangens. Oznacza to, że niezależnie od tego, jak bardzo dodasz lub odejmiesz te okresy od rozważanych kątów, wartości funkcji trygonometrycznych nie ulegną zmianie.

Na przykład, , itd.

Powrócimy później do bardziej szczegółowego wyjaśnienia i zastosowania tej właściwości funkcji trygonometrycznych.

Istnieją pewne zależności między funkcjami trygonometrycznymi tego samego argumentu, które są bardzo często używane i nazywane podstawowe tożsamości trygonometryczne.

Wyglądają tak:

1) , tak zwana „jednostka trygonometryczna”

3)

4)

5)

Należy zauważyć, że na przykład zapis oznacza, że ​​cała funkcja trygonometryczna jest podniesiona do kwadratu. Te. można to przedstawić w tej postaci: . Ważne jest, aby zrozumieć, że nie jest to równoznaczne z zapisem takim jak , w tym przypadku do kwadratu podnoszony jest tylko argument, a nie cała funkcja, a poza tym wyrażenia tego typu są niezwykle rzadkie.

Z pierwszej tożsamości wynikają dwa bardzo przydatne wnioski, które mogą być przydatne w rozwiązywaniu wielu typów problemów. Po prostych przekształceniach można wyrazić sinus przez cosinus tego samego kąta i odwrotnie:

Pojawiają się dwa możliwe znaki wyrażenia, ponieważ pobranie arytmetycznego pierwiastka kwadratowego daje tylko wartości nieujemne, a sinus i cosinus, jak już widzieliśmy, mogą mieć wartości ujemne. Co więcej, najwygodniej jest określić znaki tych funkcji za pomocą koła trygonometrycznego, w zależności od tego, jakie kąty są w nich obecne.

A teraz pamiętajmy, że kąty można mierzyć na dwa sposoby: w stopniach i w radianach. Wskażmy definicje jednego stopnia i jednego radiana.

Jeden stopień- jest to kąt utworzony przez dwa promienie tworzące łuk równy okręgowi.

Jeden radian- jest to kąt utworzony przez dwa promienie, na których opiera się łuk o długości równej promieniom.

Te. są to po prostu dwa różne sposoby pomiaru kątów, które są absolutnie równe. Opisując procesy fizyczne, które charakteryzują się funkcjami trygonometrycznymi, zwyczajowo stosuje się radianową miarę kątów, więc też będziemy musieli się do tego przyzwyczaić.

Zwyczajowo mierzy się kąty w radianach w ułamkach pi, na przykład lub. W takim przypadku można zastąpić wartość liczby „pi”, która jest równa 3,14, ale jest to rzadko wykonywane.

Aby przeliczyć stopień kąta na radiany skorzystaj z faktu, że kąt wynosi , z którego łatwo uzyskać ogólny wzór translacyjny:

Na przykład przeliczmy na radiany: .

Jest też odwrotnie formułakonwersja radianów na stopnie:

Na przykład przeliczmy na stopnie: .

W tym temacie dość często będziemy używać radianowej miary kąta.

Czas teraz przypomnieć sobie, jakie konkretne wartości mogą dawać funkcje trygonometryczne różnych kątów. Dla niektórych kątów, które są wielokrotnościami , istnieje tabela wartości funkcji trygonometrycznych. Dla wygody kąty podaje się w stopniach i radianach.

Kąty te często występują w wielu problemach i wskazane jest, aby móc pewnie poruszać się po tej tabeli. Wartości tangensów i cotangensów niektórych kątów nie mają sensu, co jest zaznaczone w tabeli jako kreski. Zastanów się, dlaczego tak jest, lub przeczytaj o tym szerzej we wkładce do lekcji.

Ostatnią rzeczą, z którą musimy się zapoznać na naszej pierwszej lekcji trygonometrii, jest transformacja funkcji trygonometrycznych za pomocą tzw. wzorów redukcyjnych.

Okazuje się, że istnieje pewien rodzaj wyrażeń dla funkcji trygonometrycznych, który jest dość powszechny i ​​wygodnie uproszczony. Są to na przykład wyrażenia: itp.

Te. Porozmawiamy o funkcjach, które przyjmują jako argument dowolny kąt, zamieniony na całość lub połowę. Takie funkcje są uproszczone do argumentu równego dowolnemu kątowi dodawania lub odejmowania części. Na przykład, , A . Jak widać, wynikiem może być funkcja odwrotna, a funkcja może zmieniać znak.

Dlatego zasady przekształcania takich funkcji można podzielić na dwa etapy. Najpierw musisz określić, jaką funkcję otrzymasz po transformacji:

1) Jeśli dowolny argument zostanie zmieniony na liczbę całkowitą, funkcja się nie zmieni. Dotyczy to funkcji typu , gdzie dowolna liczba całkowita;

Dawno, dawno temu w szkole był osobny kurs do nauki trygonometrii. Certyfikat obejmował oceny z trzech dyscyplin matematycznych: algebry, geometrii i trygonometrii.

Następnie, w ramach reformy oświaty, trygonometria przestała istnieć jako odrębny przedmiot. We współczesnej szkole pierwsza znajomość trygonometrii następuje na kursie geometrii w ósmej klasie. Bardziej dogłębna nauka tego przedmiotu jest kontynuowana na kursie algebry w 10. klasie.

Definicje sinusa, cosinusa, tangensa i cotangensa podaje się najpierw w geometrii poprzez relację boków trójkąta prostokątnego.

Kąt ostry w trójkącie prostokątnym to stosunek przeciwnej strony do przeciwprostokątnej.

Cosinus Kąt ostry w trójkącie prostokątnym to stosunek sąsiedniej nogi do przeciwprostokątnej.

Tangens Kąt ostry w trójkącie prostokątnym to stosunek boku przeciwnego do boku sąsiedniego.

Cotangens Kąt ostry w trójkącie prostokątnym to stosunek boku sąsiedniego do boku przeciwnego.

Definicje te mają zastosowanie wyłącznie do kątów ostrych (0° do 90°).

Na przykład,

w trójkącie ABC, gdzie ∠C=90°, BC to ramię przeciwne do kąta A, AC to ramię sąsiadujące z kątem A, AB to przeciwprostokątna.

Zajęcia z algebry dla klasy 10 wprowadzają definicje sinusa, cosinusa, tangensa i cotangensu dla dowolnego kąta (w tym ujemnego).

Rozważmy okrąg o promieniu R ze środkiem w początku - punkt O(0;0). Oznaczmy punkt przecięcia okręgu z dodatnim kierunkiem osi odciętej jako P 0 .

W geometrii kąt uważa się za część płaszczyzny ograniczonej dwoma promieniami. Przy tej definicji kąt zmienia się od 0° do 180°.

W trygonometrii kąt jest uważany za wynik obrotu promienia OP 0 wokół punktu początkowego O.

Jednocześnie zgodzili się rozważyć obrót belki w kierunku przeciwnym do ruchu wskazówek zegara jako dodatni kierunek przechodzenia, a zgodnie z ruchem wskazówek zegara jako ujemny (zgodność ta wiąże się z prawdziwym ruchem Słońca wokół Ziemi).

Na przykład, gdy promień OP 0 zostanie obrócony wokół punktu O o kąt α w kierunku przeciwnym do ruchu wskazówek zegara, punkt P 0 przejdzie do punktu P α,

przy obrocie o kąt α zgodnie z ruchem wskazówek zegara – do punktu F.

Przy tej definicji kąt może przyjmować dowolną wartość.

Jeżeli będziemy dalej obracać belkę OP 0 przeciwnie do ruchu wskazówek zegara, to przy obrocie o kąt α°+360°, α°+360°·2,...,α°+360°·n, gdzie n jest liczbą całkowitą (n∈ Ζ), przejdźmy ponownie do punktu P α:

Kąty mierzy się w stopniach i radianach.

1° to kąt równy 1/180 miary stopnia rozwiniętego kąta.

1 radian to kąt środkowy, którego długość łuku jest równa promieniowi okręgu:

∠AOB=1 rad.

Symbole radianów zwykle nie są zapisywane. W protokole nie można pominąć oznaczenia stopnia.

Na przykład,

Punkt P α , otrzymany z punktu P 0 poprzez obrót promienia OP 0 wokół punktu O o kąt α w kierunku przeciwnym do ruchu wskazówek zegara, ma współrzędne P α (x;y).

Upuśćmy prostopadłą P α A z punktu P α do osi odciętej.

W trójkącie prostokątnym OP α A:

P α A - noga przeciwna do kąta α,

OA - noga przylegająca do kąta α,

OP α jest przeciwprostokątną.

P α A=y, OA=x, OP α =R.

Z definicji sinusa, cosinusa, tangensa i cotangensa w trójkącie prostokątnym mamy:

Zatem w przypadku okręgu o środku w początku dowolnego promienia sinus kąt α jest stosunkiem rzędnej punktu P α do długości promienia.

Cosinus kąt α jest stosunkiem odciętej punktu P α do długości promienia.

Tangens kąt α jest stosunkiem rzędnej punktu P α do jego odciętej.

Cotangens kąt α jest stosunkiem odciętej punktu P α do jego rzędnej.

Wartości sinusa, cosinusa, tangensa i cotangensu zależą tylko od wartości α i nie zależą od długości promienia R (wynika to z podobieństwa okręgów).

Dlatego wygodnie jest wybrać R=1.

Okrąg o środku w początku i promieniu R=1 nazywa się kołem jednostkowym.

Definicje

1) Zatoka kąt α nazywany jest rzędną punktu P α (x;y) okręgu jednostkowego:

2) Cosinus kąt α nazywany jest odciętą punktu P α (x;y) okręgu jednostkowego:

3) Tangens kąt α jest stosunkiem rzędnych punktu P α (x;y) do jego odciętej, czyli stosunkiem sinα do cosα (gdzie cosα≠0):

4) Cotangens kąt α jest stosunkiem odciętej punktu P α (x;y) do jego rzędnej, czyli stosunku cosα do sinα (gdzie sinα≠0):

Wprowadzone w ten sposób definicje pozwalają uwzględnić nie tylko funkcje trygonometryczne kątów, ale także funkcje trygonometryczne argumentów liczbowych (jeśli uznamy sinα, cosα, tanα i ctgα za odpowiadające im funkcje trygonometryczne kąta w α radianach, czyli sinus liczby α jest sinusem kąta w α radianach, cosinus liczby α jest cosinusem kąta w α radianach itd.).

Własności funkcji trygonometrycznych są studiowane jako odrębny temat na kursie algebry w klasach 10 lub 11. Funkcje trygonometryczne są szeroko stosowane w fizyce.

Sinus, cosinus, tangens – wymawiając te słowa w obecności licealistów, możesz być pewien, że dwie trzecie z nich straci zainteresowanie dalszą rozmową. Powodem jest to, że podstaw trygonometrii w szkole uczy się w całkowitym oderwaniu od rzeczywistości, dlatego uczniowie nie widzą sensu studiowania wzorów i twierdzeń.

Rzeczywiście, po bliższym przyjrzeniu się, ta dziedzina wiedzy okazuje się bardzo interesująca, a także stosowana - trygonometrię wykorzystuje się w astronomii, budownictwie, fizyce, muzyce i wielu innych dziedzinach.

Zapoznajmy się z podstawowymi pojęciami i wymieńmy kilka powodów, dla których warto studiować tę gałąź nauk matematycznych.

Fabuła

Nie wiadomo, w którym momencie ludzkość zaczęła od zera tworzyć przyszłą trygonometrię. Udokumentowano jednak, że już w drugim tysiącleciu p.n.e. Egipcjanie znali podstawy tej nauki: archeolodzy znaleźli papirus z zadaniem, w którym należało znaleźć kąt nachylenia piramidy z dwóch znanych stron.

Naukowcy starożytnego Babilonu odnieśli poważniejsze sukcesy. Na przestrzeni wieków, studiując astronomię, opanowali szereg twierdzeń, wprowadzili specjalne metody pomiaru kątów, które, nawiasem mówiąc, używamy dzisiaj: stopnie, minuty i sekundy zostały zapożyczone przez naukę europejską w kulturze grecko-rzymskiej, do której jednostki te pochodziły z Babilończyków.

Zakłada się, że słynne twierdzenie Pitagorasa, dotyczące podstaw trygonometrii, było znane Babilończykom prawie cztery tysiące lat temu.

Nazwa

Dosłownie termin „trygonometria” można przetłumaczyć jako „pomiar trójkątów”. Głównym przedmiotem badań w tej sekcji nauki przez wiele stuleci był trójkąt prostokątny, a ściślej związek między wielkościami kątów a długościami jego boków (dziś badanie trygonometrii od podstaw rozpoczyna się od tej sekcji) . Często w życiu zdarzają się sytuacje, gdy praktycznie niemożliwe jest zmierzenie wszystkich wymaganych parametrów obiektu (lub odległości do obiektu), a wtedy konieczne staje się uzyskanie brakujących danych poprzez obliczenia.

Na przykład w przeszłości ludzie nie potrafili mierzyć odległości do obiektów kosmicznych, ale próby obliczenia tych odległości miały miejsce na długo przed nadejściem naszej ery. Trygonometria również odegrała kluczową rolę w nawigacji: przy odrobinie wiedzy kapitan mógł zawsze nawigować nocą według gwiazd i korygować kurs.

Podstawowe koncepcje

Opanowanie trygonometrii od podstaw wymaga zrozumienia i zapamiętania kilku podstawowych pojęć.

Sinus pewnego kąta to stosunek przeciwnej strony do przeciwprostokątnej. Wyjaśnijmy, że przeciwna noga to strona leżąca naprzeciwko kąta, który rozważamy. Zatem, jeśli kąt wynosi 30 stopni, sinus tego kąta będzie zawsze, dla dowolnej wielkości trójkąta, równy ½. Cosinus kąta to stosunek sąsiedniej nogi do przeciwprostokątnej.

Tangens to stosunek strony przeciwnej do strony sąsiedniej (lub, co jest takie samo, stosunek sinusa do cosinusa). Cotangens to jednostka podzielona przez styczną.

Warto wspomnieć o słynnej liczbie Pi (3,14...), która stanowi połowę długości koła o promieniu jednej jednostki.

Popularne błędy

Osoby uczące się trygonometrii od podstaw popełniają szereg błędów – głównie z powodu nieuwagi.

Po pierwsze, rozwiązując problemy z geometrią, należy pamiętać, że użycie sinusów i cosinusów jest możliwe tylko w trójkącie prostokątnym. Zdarza się, że uczeń „automatycznie” przyjmuje za przeciwprostokątną najdłuższy bok trójkąta i otrzymuje błędne wyniki obliczeń.

Po drugie, na początku łatwo jest pomylić wartości sinusa i cosinusa dla wybranego kąta: pamiętaj, że sinus 30 stopni jest liczbowo równy cosinusowi 60 i odwrotnie. Jeśli zastąpisz nieprawidłową liczbę, wszystkie dalsze obliczenia będą nieprawidłowe.

Po trzecie, dopóki problem nie zostanie całkowicie rozwiązany, nie należy zaokrąglać żadnych wartości, wyodrębniać pierwiastków ani zapisywać ułamka zwykłego w postaci ułamka dziesiętnego. Często uczniowie starają się uzyskać „piękną” liczbę w zadaniu trygonometrycznym i natychmiast wyodrębniają pierwiastek z trzech, chociaż po dokładnie jednym działaniu pierwiastek ten można zmniejszyć.

Etymologia słowa „sinus”

Historia słowa „sinus” jest naprawdę niezwykła. Faktem jest, że dosłowne tłumaczenie tego słowa z łaciny oznacza „pusty”. Dzieje się tak, ponieważ prawidłowe zrozumienie tego słowa zostało utracone podczas tłumaczenia z jednego języka na drugi.

Nazwy podstawowych funkcji trygonometrycznych wywodzą się z Indii, gdzie pojęcie sinusa w sanskrycie oznaczano słowem „sznurek” – faktem jest, że odcinek wraz z łukiem koła, na którym spoczywał, wyglądał jak łuk . W okresie rozkwitu cywilizacji arabskiej zapożyczono indyjskie osiągnięcia z zakresu trygonometrii, a termin ten przeszedł na język arabski w formie transkrypcji. Tak się złożyło, że w tym języku istniało już podobne słowo oznaczające depresję i jeśli Arabowie zrozumieli różnicę fonetyczną między słowem rodzimym a zapożyczonym, to Europejczycy, tłumacząc traktaty naukowe na łacinę, błędnie dosłownie przetłumaczyli arabskie słowo, które nie miało nic ma to związek z pojęciem sinusa. Używamy go do dziś.

Tablice wartości

Istnieją tabele zawierające wartości liczbowe sinusów, cosinusów i stycznych wszystkich możliwych kątów. Poniżej prezentujemy dane dla kątów 0, 30, 45, 60 i 90 stopni, których trzeba się nauczyć jako obowiązkowej części trygonometrii dla „manekinów”, na szczęście są one dość łatwe do zapamiętania;

Jeśli zdarzy się, że wartość liczbowa sinusa lub cosinusa kąta „wyleciała ci z głowy”, istnieje sposób, aby wyprowadzić ją samodzielnie.

Reprezentacja geometryczna

Narysujmy okrąg i przez jego środek narysujmy odciętą i osie rzędnych. Oś odciętych jest pozioma, oś rzędnych jest pionowa. Zazwyczaj są one oznaczone odpowiednio jako „X” i „Y”. Teraz narysujemy linię prostą ze środka okręgu, aby uzyskać potrzebny kąt między nim a osią X. Wreszcie z punktu, w którym prosta przecina okrąg, upuszczamy prostopadłą do osi X. Długość powstałego odcinka będzie równa wartości liczbowej sinusa naszego kąta.

Ta metoda jest bardzo istotna, jeśli zapomniałeś wymaganej wartości na przykład podczas egzaminu i nie masz pod ręką podręcznika do trygonometrii. W ten sposób nie uzyskasz dokładnej liczby, ale na pewno zobaczysz różnicę między ½ a 1,73/2 (sinus i cosinus kąta 30 stopni).

Aplikacja

Jednymi z pierwszych ekspertów, którzy zastosowali trygonometrię, byli żeglarze, którzy na pełnym morzu nie mieli innego punktu odniesienia poza niebem nad swoimi głowami. Dziś kapitanowie statków (samolotów i innych środków transportu) nie szukają najkrótszej drogi korzystając z gwiazd, lecz aktywnie korzystają z nawigacji GPS, co nie byłoby możliwe bez zastosowania trygonometrii.

W niemal każdym dziale fizyki znajdziesz obliczenia z wykorzystaniem sinusów i cosinusów: czy to zastosowanie siły w mechanice, obliczenia toru obiektów w kinematyce, drgania, propagacja fal, załamanie światła - po prostu nie da się obejść się bez podstawowej trygonometrii w formuły.

Kolejnym zawodem, który jest nie do pomyślenia bez trygonometrii, jest geodeta. Za pomocą teodolitu i poziomicy lub bardziej złożonego urządzenia - tachometru, osoby te mierzą różnicę wysokości pomiędzy różnymi punktami na powierzchni ziemi.

Powtarzalność

Trygonometria zajmuje się nie tylko kątami i bokami trójkąta, chociaż od tego zaczęła swoje istnienie. We wszystkich dziedzinach, w których występuje cykliczność (biologia, medycyna, fizyka, muzyka itp.) natkniesz się na wykres, którego nazwa jest prawdopodobnie Ci znana - jest to fala sinusoidalna.

Taki wykres jest okręgiem rozwiniętym wzdłuż osi czasu i wygląda jak fala. Jeśli kiedykolwiek pracowałeś z oscyloskopem na lekcjach fizyki, wiesz, o czym mówimy. Zarówno korektor muzyczny, jak i pulsometr wykorzystują w swoim działaniu wzory trygonometryczne.

Wreszcie

Myśląc o nauce trygonometrii, większość uczniów gimnazjów i liceów zaczyna uważać ją za naukę trudną i niepraktyczną, ponieważ zapoznają się jedynie z nudnymi informacjami z podręcznika.

Jeśli chodzi o niepraktyczność, widzieliśmy już, że w takim czy innym stopniu umiejętność obsługi sinusów i stycznych jest wymagana w prawie każdej dziedzinie działalności. A co do złożoności... Pomyśl: jeśli ludzie korzystali z tej wiedzy ponad dwa tysiące lat temu, kiedy dorosły miał mniejszą wiedzę niż dzisiejszy licealista, czy dla Ciebie realne jest studiowanie tej dziedziny nauki na poziomie podstawowym? Kilka godzin przemyślanej praktyki rozwiązywania problemów - a osiągniesz swój cel studiując kurs podstawowy, tzw. trygonometrię dla manekinów.