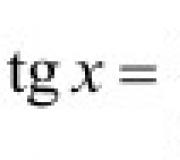त्रिकोणमिती सोपी आणि स्पष्ट आहे. त्रिकोणमिती त्रिकोणमितीय कार्ये स्पष्ट केली
त्रिकोणमितीय रूपांतरणे करताना, या टिपांचे अनुसरण करा:
- सुरुवातीपासून शेवटपर्यंत उदाहरणावर त्वरित उपाय शोधण्याचा प्रयत्न करू नका.
- संपूर्ण उदाहरण एकाच वेळी रूपांतरित करण्याचा प्रयत्न करू नका. छोटी पावले पुढे टाका.
- लक्षात ठेवा की त्रिकोणमितीमधील त्रिकोणमितीय सूत्रांव्यतिरिक्त, तुम्ही तरीही सर्व निष्पक्ष बीजगणितीय परिवर्तने (कंस, संक्षिप्त अपूर्णांक, संक्षिप्त गुणाकार सूत्रे इ.) वापरू शकता.
- सर्व काही ठीक होईल यावर विश्वास ठेवा.
मूळ त्रिकोणमितीय सूत्रे
त्रिकोणमितीमधील बहुतेक सूत्रे उजवीकडून डावीकडे आणि डावीकडून उजवीकडे दोन्ही वापरली जातात, त्यामुळे तुम्हाला ही सूत्रे इतक्या चांगल्या प्रकारे शिकण्याची गरज आहे की तुम्ही दोन्ही दिशांना काही सूत्र सहजपणे लागू करू शकता. प्रथम त्रिकोणमितीय फंक्शन्सच्या व्याख्या लिहू. एक काटकोन त्रिकोण असू द्या:
मग, साइनची व्याख्या:
कोसाइनची व्याख्या:
स्पर्शिका व्याख्या:
![]()
कोटँजेंटची व्याख्या:

मूळ त्रिकोणमितीय ओळख:
मूळ त्रिकोणमितीय ओळखीतील सर्वात सोपी परिणाम:
![]()
![]()
दुहेरी कोन सूत्रे.दुहेरी कोनाची साइन:

दुहेरी कोनाचा कोसाइन:
दुहेरी कोनाची स्पर्शिका:

दुहेरी कोनाचे कोटँजेंट:

अतिरिक्त त्रिकोणमितीय सूत्रे
त्रिकोणमितीय जोड सूत्रे.बेरीजचे साइन:
फरकाची साइन:
बेरीजचे कोसाइन:
फरकाचा कोसाइन:
बेरीजची स्पर्शिका:

फरकाची स्पर्शिका:

रकमेचा स्पर्शक:
फरकाचा स्पर्शक:
बेरीजचे उत्पादनामध्ये रूपांतर करण्यासाठी त्रिकोणमितीय सूत्रे.साइन्सची बेरीज:
साइन फरक:
कोसाइनची बेरीज:
कोसाइनमधील फरक:
स्पर्शिकेची बेरीज:

स्पर्शिका फरक:

कोटँजंट्सची बेरीज:

कोटँजेंट फरक:

उत्पादनाचे बेरीजमध्ये रूपांतर करण्यासाठी त्रिकोणमितीय सूत्रे.सायन्सचे उत्पादन:
साइन आणि कोसाइनचे उत्पादन:
कोसाइनचे उत्पादन:
पदवी कमी करण्याचे सूत्र.
![]()
![]()
![]()
![]()
अर्धकोन सूत्रे.
![]()
![]()
त्रिकोणमितीय घट सूत्रे
कोसाइन फंक्शन म्हणतात सहसंबंध sine फंक्शन्स आणि त्याउलट. त्याचप्रमाणे, स्पर्शिका आणि कोटँजेंट फंक्शन्स हे सहसंबंध आहेत. कमी करण्याचे सूत्र खालील नियमानुसार तयार केले जाऊ शकतात:
- जर रिडक्शन फॉर्म्युलामध्ये कोन 90 अंश किंवा 270 अंशांमधून वजा (जोडला) असेल, तर घटलेले कार्य कॉफंक्शनमध्ये बदलते;
- जर रिडक्शन फॉर्म्युलामध्ये 180 डिग्री किंवा 360 डिग्री मधून कोन वजा (जोडला) असेल, तर कमी केलेल्या फंक्शनचे नाव कायम ठेवले जाते;
- या प्रकरणात, कमी केलेले (म्हणजे मूळ) फंक्शन संबंधित क्वाड्रंटमध्ये असलेले चिन्ह कमी केलेल्या फंक्शनच्या समोर ठेवले जाते, जर आपण वजा (जोडलेला) कोन तीव्र आहे असे मानले तर.
कपात सूत्रेसारणी स्वरूपात दिले आहेत:

द्वारे त्रिकोणमितीय वर्तुळत्रिकोणमितीय कार्यांची सारणी मूल्ये निर्धारित करणे सोपे:

त्रिकोणमितीय समीकरणे
विशिष्ट त्रिकोणमितीय समीकरण सोडवण्यासाठी, ते सर्वात सोप्या त्रिकोणमितीय समीकरणांपैकी एकापर्यंत कमी केले पाहिजे, ज्याची खाली चर्चा केली जाईल. यासाठी:
- तुम्ही वर दिलेली त्रिकोणमितीय सूत्रे वापरू शकता. त्याच वेळी, तुम्हाला संपूर्ण उदाहरण एकाच वेळी बदलण्याचा प्रयत्न करण्याची आवश्यकता नाही, परंतु तुम्हाला लहान चरणांमध्ये पुढे जाण्याची आवश्यकता आहे.
- बीजगणितीय पद्धती वापरून काही अभिव्यक्ती बदलण्याच्या शक्यतेबद्दल आपण विसरू नये, म्हणजे. उदाहरणार्थ, कंसातून काहीतरी घ्या किंवा, उलट, कंस उघडा, एक अपूर्णांक कमी करा, एक संक्षिप्त गुणाकार सूत्र लागू करा, अपूर्णांकांना सामान्य भाजकात आणा आणि असेच.
- त्रिकोणमितीय समीकरणे सोडवताना, तुम्ही वापरू शकता गटबद्ध पद्धत. हे लक्षात ठेवले पाहिजे की अनेक घटकांचे उत्पादन शून्याच्या बरोबरीसाठी, त्यापैकी कोणतेही शून्य समान असणे पुरेसे आहे आणि बाकीचे अस्तित्वात होते.
- अर्ज करत आहे व्हेरिएबल बदलण्याची पद्धत, नेहमीप्रमाणे, प्रतिस्थापन सादर केल्यानंतर समीकरण सोपे झाले पाहिजे आणि त्यात मूळ चल नसावे. तुम्हाला रिव्हर्स रिप्लेसमेंट करणे देखील लक्षात ठेवणे आवश्यक आहे.
- लक्षात ठेवा की त्रिकोणमितीमध्ये एकसंध समीकरणे अनेकदा दिसतात.
- मॉड्यूल्स उघडताना किंवा त्रिकोणमितीय फंक्शन्ससह अतार्किक समीकरणे सोडवताना, तुम्हाला सामान्य फंक्शन्ससह संबंधित समीकरणे सोडवण्याच्या सर्व बारकावे लक्षात ठेवणे आणि विचारात घेणे आवश्यक आहे.
- ODZ बद्दल लक्षात ठेवा (त्रिकोणमितीय समीकरणांमध्ये, ODZ वरील निर्बंध प्रामुख्याने खाली येतात की आपण शून्याने विभाजित करू शकत नाही, परंतु इतर निर्बंधांबद्दल विसरू नका, विशेषत: तर्कसंगत शक्तींमधील अभिव्यक्तीच्या सकारात्मकतेबद्दल आणि सम शक्तींच्या मुळांच्या खाली). हे देखील लक्षात ठेवा की साइन आणि कोसाइनची मूल्ये फक्त वजा एक ते प्लस वन या श्रेणीत असू शकतात, सर्वसमावेशक.
मुख्य गोष्ट म्हणजे, जर तुम्हाला काय करावे हे माहित नसेल तर किमान काहीतरी करा आणि मुख्य म्हणजे त्रिकोणमितीय सूत्रे योग्यरित्या वापरणे. जर तुम्हाला जे मिळते ते चांगले आणि चांगले होत असेल तर उपाय चालू ठेवा आणि जर ते खराब झाले तर सुरुवातीस परत जा आणि इतर सूत्रे लागू करण्याचा प्रयत्न करा, जोपर्यंत तुम्हाला योग्य उपाय सापडत नाही तोपर्यंत हे करा.
सर्वात सोप्या त्रिकोणमितीय समीकरणांच्या निराकरणासाठी सूत्रे.साइनसाठी सोल्यूशन लिहिण्याचे दोन समतुल्य प्रकार आहेत:
इतर त्रिकोणमितीय कार्यांसाठी, नोटेशन अस्पष्ट आहे. कोसाइनसाठी:
स्पर्शिकेसाठी:
कोटँजंटसाठी:
काही विशेष प्रकरणांमध्ये त्रिकोणमितीय समीकरणे सोडवणे:
या तीन मुद्यांची यशस्वी, परिश्रमपूर्वक आणि जबाबदारीने अंमलबजावणी केल्याने तुम्हाला CT वर उत्कृष्ट परिणाम दाखवता येतील, तुमच्या क्षमतेपेक्षा जास्तीत जास्त.
चूक सापडली?
तुम्हाला प्रशिक्षण सामग्रीमध्ये त्रुटी आढळली आहे असे तुम्हाला वाटत असल्यास, कृपया त्याबद्दल ईमेलद्वारे लिहा. आपण सामाजिक नेटवर्क () वर त्रुटीची तक्रार देखील करू शकता. पत्रात, विषय (भौतिकशास्त्र किंवा गणित), विषय किंवा चाचणीचे नाव किंवा संख्या, समस्येची संख्या किंवा मजकूरातील जागा (पृष्ठ) सूचित करा जिथे, तुमच्या मते, त्रुटी आहे. संशयित त्रुटी काय आहे ते देखील वर्णन करा. तुमच्या पत्राकडे लक्ष दिले जाणार नाही, त्रुटी एकतर दुरुस्त केली जाईल किंवा ती त्रुटी का नाही हे तुम्हाला स्पष्ट केले जाईल.
तुमची गोपनीयता राखणे आमच्यासाठी महत्त्वाचे आहे. या कारणास्तव, आम्ही एक गोपनीयता धोरण विकसित केले आहे जे आम्ही तुमची माहिती कशी वापरतो आणि संचयित करतो याचे वर्णन करते. कृपया आमच्या गोपनीयता पद्धतींचे पुनरावलोकन करा आणि तुम्हाला काही प्रश्न असल्यास आम्हाला कळवा.
वैयक्तिक माहितीचे संकलन आणि वापर
वैयक्तिक माहिती डेटाचा संदर्भ देते ज्याचा वापर एखाद्या विशिष्ट व्यक्तीला ओळखण्यासाठी किंवा त्याच्याशी संपर्क साधण्यासाठी केला जाऊ शकतो.
तुम्ही आमच्याशी संपर्क साधता तेव्हा तुम्हाला तुमची वैयक्तिक माहिती देण्यास सांगितले जाऊ शकते.
खाली आम्ही एकत्रित केलेल्या वैयक्तिक माहितीच्या प्रकारांची आणि आम्ही अशी माहिती कशी वापरू शकतो याची काही उदाहरणे दिली आहेत.
आम्ही कोणती वैयक्तिक माहिती गोळा करतो:
- तुम्ही साइटवर अर्ज सबमिट करता तेव्हा, आम्ही तुमचे नाव, फोन नंबर, ईमेल पत्ता इत्यादीसह विविध माहिती गोळा करू शकतो.
आम्ही तुमची वैयक्तिक माहिती कशी वापरतो:
- आम्ही संकलित केलेली वैयक्तिक माहिती आम्हाला अनन्य ऑफर, जाहिराती आणि इतर कार्यक्रम आणि आगामी कार्यक्रमांसह तुमच्याशी संपर्क साधण्याची अनुमती देते.
- वेळोवेळी, महत्त्वाच्या सूचना आणि संप्रेषणे पाठवण्यासाठी आम्ही तुमची वैयक्तिक माहिती वापरू शकतो.
- आम्ही प्रदान करत असल्या सेवा सुधारण्यासाठी आणि तुम्हाला आमच्या सेवांसंबंधी शिफारशी प्रदान करण्यासाठी ऑडिट, डेटा विश्लेषण आणि विविध संशोधन करण्यासाठी आम्ही अंतर्गत उद्देशांसाठी वैयक्तिक माहिती देखील वापरू शकतो.
- तुम्ही बक्षीस सोडत, स्पर्धा किंवा तत्सम जाहिरातींमध्ये भाग घेतल्यास, आम्ही अशा कार्यक्रमांचे व्यवस्थापन करण्यासाठी तुम्ही प्रदान केलेली माहिती वापरू शकतो.
तृतीय पक्षांना माहितीचे प्रकटीकरण
तुमच्याकडून मिळालेली माहिती आम्ही तृतीय पक्षांना उघड करत नाही.
अपवाद:
- आवश्यक असल्यास - कायद्यानुसार, न्यायालयीन प्रक्रियेनुसार, कायदेशीर कार्यवाहीमध्ये आणि/किंवा सार्वजनिक विनंत्या किंवा रशियन फेडरेशनच्या प्रदेशातील सरकारी अधिकाऱ्यांच्या विनंत्यांच्या आधारावर - तुमची वैयक्तिक माहिती उघड करणे. सुरक्षा, कायद्याची अंमलबजावणी किंवा इतर सार्वजनिक महत्त्वाच्या उद्देशांसाठी असे प्रकटीकरण आवश्यक किंवा योग्य आहे हे आम्ही निर्धारित केल्यास आम्ही तुमच्याबद्दलची माहिती देखील उघड करू शकतो.
- पुनर्रचना, विलीनीकरण किंवा विक्री झाल्यास, आम्ही संकलित केलेली वैयक्तिक माहिती लागू उत्तराधिकारी तृतीय पक्षाकडे हस्तांतरित करू शकतो.
वैयक्तिक माहितीचे संरक्षण
तुमच्या वैयक्तिक माहितीचे नुकसान, चोरी आणि गैरवापर, तसेच अनधिकृत प्रवेश, प्रकटीकरण, बदल आणि विनाश यापासून संरक्षण करण्यासाठी आम्ही - प्रशासकीय, तांत्रिक आणि भौतिक यासह - खबरदारी घेतो.
कंपनी स्तरावर तुमच्या गोपनीयतेचा आदर करणे
तुमची वैयक्तिक माहिती सुरक्षित असल्याची खात्री करण्यासाठी, आम्ही आमच्या कर्मचाऱ्यांना गोपनीयता आणि सुरक्षा मानके संप्रेषण करतो आणि गोपनीयता पद्धतींची काटेकोरपणे अंमलबजावणी करतो.
या धड्यात आपण व्याख्या शिकू त्रिकोणमितीय कार्ये आणि त्यांचे मूलभूत गुणधर्म, सोबत काम कसे करायचे ते शिका त्रिकोणमितीय वर्तुळ, ते काय आहे ते जाणून घेऊया कार्य कालावधीआणि विविध लक्षात ठेवा कोन मोजण्याचे मार्ग. याव्यतिरिक्त, आम्ही वापर समजून घेऊ कपात सूत्रे.
हा धडा तुम्हाला कार्यांच्या प्रकारांपैकी एकाची तयारी करण्यास मदत करेल एटी 7.
गणितातील युनिफाइड स्टेट परीक्षेची तयारी
प्रयोग
धडा 7.त्रिकोणमितीचा परिचय.
सिद्धांत
धडा सारांश
आज आम्ही एक विभाग सुरू करत आहोत ज्याचे नाव "त्रिकोनोमेट्री" अनेकांसाठी भितीदायक आहे. चला हे लगेच स्पष्ट करूया की हा भूमितीच्या नावासारखा वेगळा विषय नाही, जसे काही लोकांना वाटते. जरी ग्रीकमधून अनुवादित "त्रिकोणमिति" या शब्दाचा अर्थ "त्रिकोणांचे मोजमाप" आहे आणि तो थेट भूमितीशी संबंधित आहे. याव्यतिरिक्त, भौतिकशास्त्र आणि तंत्रज्ञानामध्ये त्रिकोणमितीय गणना मोठ्या प्रमाणावर वापरली जाते. परंतु आपण काटकोन त्रिकोण वापरून भूमितीमध्ये मूलभूत त्रिकोणमितीय कार्ये कशी सादर केली जातात याचा विचार करून सुरुवात करू.
आम्ही फक्त "त्रिकोनोमेट्रिक फंक्शन" हा शब्द वापरला आहे - याचा अर्थ असा की आम्ही एका व्हेरिएबल आणि दुसऱ्या व्हेरिएबलमधील पत्रव्यवहाराच्या विशिष्ट नियमांचा संपूर्ण वर्ग सादर करू.
हे करण्यासाठी, एका काटकोन त्रिकोणाचा विचार करा, ज्यामध्ये, सोयीसाठी, बाजू आणि कोनांसाठी मानक नोटेशन्स वापरली जातात, जी आपण आकृतीमध्ये पाहू शकता:
उदाहरणार्थ, कोन विचारात घ्याआणि त्यासाठी खालील क्रिया प्रविष्ट करा:
कर्ण साइनच्या विरुद्ध बाजूचे गुणोत्तर म्हणू, म्हणजे.
कर्ण कोसाइनच्या समीप पायाचे गुणोत्तर म्हणू, म्हणजे. ;
समीप बाजूच्या विरुद्ध बाजूचे गुणोत्तर स्पर्शिका म्हटले जाईल, म्हणजे. ;
समीप बाजूच्या विरुद्ध बाजूच्या गुणोत्तराला कोटँजेंट म्हटले जाईल, म्हणजे. .
कोन असलेल्या या सर्व क्रिया म्हणतात त्रिकोणमितीय कार्ये. कोन स्वतःला सहसा म्हणतात त्रिकोणमितीय कार्याचा युक्तिवादआणि हे दर्शविले जाऊ शकते, उदाहरणार्थ, X द्वारे, सामान्यतः बीजगणित मध्ये प्रथा आहे.
हे त्वरित समजून घेणे महत्त्वाचे आहे की त्रिकोणमितीय कार्ये विशेषतः काटकोन त्रिकोणातील कोनावर अवलंबून असतात, त्याच्या बाजूंवर नाही. या सारख्या त्रिकोणाचा विचार केल्यास हे सिद्ध करणे सोपे आहे, ज्यामध्ये बाजूंची लांबी भिन्न असेल, परंतु बाजूंचे सर्व कोन आणि गुणोत्तर बदलणार नाहीत, म्हणजे. कोनांची त्रिकोणमितीय कार्ये देखील अपरिवर्तित राहतील.
त्रिकोणमितीय कार्यांच्या या व्याख्येनंतर, प्रश्न उद्भवू शकतो: "तेथे आहे, उदाहरणार्थ,? सर्व केल्यानंतर, कोपराकाटकोन त्रिकोणात असू शकत नाही» . विचित्रपणे, या प्रश्नाचे उत्तर होकारार्थी आहे, आणि या अभिव्यक्तीचे मूल्य समान आहे, आणि हे आणखी आश्चर्यकारक आहे, कारण सर्व त्रिकोणमितीय कार्ये काटकोन त्रिकोणाच्या बाजूंचे गुणोत्तर आहेत आणि बाजूंच्या लांबी आहेत. सकारात्मक संख्या.
पण यात विरोधाभास नाही. वस्तुस्थिती अशी आहे की, उदाहरणार्थ, भौतिकशास्त्रात, काही प्रक्रियांचे वर्णन करताना, कोनांची त्रिकोणमितीय फंक्शन्स केवळ मोठ्याच नव्हे तर मोठ्या आणि समान देखील वापरणे आवश्यक आहे. हे करण्यासाठी, तथाकथित वापरून त्रिकोणमितीय फंक्शन्सची गणना करण्यासाठी अधिक सामान्य नियम लागू करणे आवश्यक आहे "एकक त्रिकोणमितीय वर्तुळ".
हे एकक त्रिज्या असलेले वर्तुळ आहे, असे काढले आहे की त्याचे केंद्र कार्टेशियन विमानाच्या उगमस्थानी आहे.
 |
या वर्तुळातील कोनांचे चित्रण करण्यासाठी, ते कोठून ठेवायचे यावर तुम्ही सहमत असणे आवश्यक आहे. कोन संदर्भ किरण म्हणून abscissa अक्षाची सकारात्मक दिशा घेणे स्वीकारले जाते, म्हणजे. x-अक्ष. कोनांच्या निक्षेपाची दिशा घड्याळाच्या विरुद्ध दिशेने मानली जाते.या करारांवर आधारित, प्रथम तीव्र कोन बाजूला ठेवूया. हे अशा तीव्र कोनांसाठी आहे की काटकोन त्रिकोणात त्रिकोणमितीय फंक्शन्सची मूल्ये कशी काढायची हे आपल्याला आधीच माहित आहे. असे दिसून आले की चित्रित वर्तुळाचा वापर करून आपण त्रिकोणमितीय कार्ये देखील मोजू शकता, फक्त अधिक सोयीस्करपणे.
तीव्र कोनाच्या साइन आणि कोसाइनची मूल्ये या कोनाच्या बाजूच्या छेदनबिंदूच्या एकक वर्तुळासह समन्वय आहेत:
हे असे लिहिले जाऊ शकते:
![]() :
:
त्या वस्तुस्थितीवर आधारित x-अक्षाच्या बाजूचे समन्वय कोसाइनचे मूल्य दर्शवतात आणि y-अक्षावरील समन्वय कोनाच्या साइनचे मूल्य दर्शवतात, तुम्ही आकृतीत पाहिल्याप्रमाणे एकक वर्तुळासह समन्वय प्रणालीमध्ये अक्षांची नावे पुनर्नामित करणे सोयीचे आहे:
 |
abscissa अक्षाचे नामकरण कोसाइन अक्ष असे केले जाते आणि ऑर्डिनेट अक्षाचे साइन अक्ष असे केले जाते.
साइन आणि कोसाइन निर्धारित करण्यासाठी निर्दिष्ट नियम हे ते पर्यंतच्या श्रेणीमध्ये असलेल्या स्थूल कोन आणि कोन दोन्हीसाठी सामान्यीकृत आहे. या प्रकरणात, साइन्स आणि कोसाइन सकारात्मक आणि नकारात्मक दोन्ही मूल्ये घेऊ शकतात. विविध या त्रिकोणमितीय कार्यांच्या मूल्यांची चिन्हेप्रश्नातील कोन कोणत्या तिमाहीत येतो यावर अवलंबून, ते खालीलप्रमाणे चित्रित करण्याची प्रथा आहे:

जसे आपण पाहू शकता, त्रिकोणमितीय कार्यांची चिन्हे त्यांच्या संबंधित अक्षांच्या सकारात्मक आणि नकारात्मक दिशानिर्देशांद्वारे निर्धारित केली जातात.
याव्यतिरिक्त, हे लक्षात घेण्यासारखे आहे की एकक वर्तुळावरील बिंदूचा सर्वात मोठा समन्वय ऍब्सिसिसा आणि ऑर्डिनेट अक्ष या दोन्ही बाजूने समान आहे आणि सर्वात लहान वजा एक आहे. साइन आणि कोसाइन मूल्येया संख्यांपुरती मर्यादित:
![]()
![]()
हे रेकॉर्ड देखील सहसा या फॉर्ममध्ये लिहिलेले असतात:
त्रिकोणमितीय वर्तुळावर स्पर्शिका आणि कोटँजेंटची कार्ये ओळखण्यासाठी, अतिरिक्त घटक काढणे आवश्यक आहे: बिंदू A वर वर्तुळाची स्पर्शिका - कोनाच्या स्पर्शिकेचे मूल्य त्यातून निर्धारित केले जाते, आणि स्पर्शिका येथे बिंदू B - कोनाच्या कोटँजंटचे मूल्य त्यातून निर्धारित केले जाते.
 |
|||
 |
तथापि, आम्ही त्रिकोणमितीय वर्तुळावरील स्पर्शिका आणि कोटॅन्जंट्सच्या व्याख्येचा शोध घेणार नाही, कारण दिलेल्या कोनातील साइन आणि कोसाइनची मूल्ये जाणून घेऊन त्यांची सहज गणना केली जाऊ शकते, जी कशी करायची हे आपल्याला आधीच माहित आहे. त्रिकोणमितीय वर्तुळावर स्पर्शिका आणि कोटँजंटची गणना कशी करायची हे शिकण्यात तुम्हाला स्वारस्य असल्यास, 10 व्या वर्गाच्या बीजगणित अभ्यासक्रमाचे पुनरावलोकन करा.
आम्ही फक्त वर्तुळावरील प्रतिमा सूचित करतो स्पर्शिका आणि कोटँजेंट्सची चिन्हेकोनावर अवलंबून:

लक्षात ठेवा, साइन आणि कोसाइन मूल्यांच्या श्रेणींप्रमाणेच, तुम्ही स्पर्शिका आणि कोटँजंट मूल्यांच्या श्रेणी निर्दिष्ट करू शकता. त्रिकोणमितीय वर्तुळावरील त्यांच्या व्याख्येवर आधारित, या फंक्शन्सचे अर्थ मर्यादित नाहीत:
![]()
![]()
यासारखे आणखी काय लिहिले जाऊ शकते:
पासून ते पर्यंत श्रेणीतील कोनांच्या व्यतिरिक्त, त्रिकोणमितीय वर्तुळ आपल्याला मोठ्या कोनांसह आणि अगदी नकारात्मक कोनांसह कार्य करण्यास अनुमती देते. अशी कोन मूल्ये, जरी ती भूमितीसाठी निरर्थक वाटत असली तरी, काही भौतिक प्रक्रियांचे वर्णन करण्यासाठी वापरली जातात. उदाहरणार्थ, तुम्ही प्रश्नाचे उत्तर कसे द्याल: "एका दिवसात घड्याळाचा हात कोणत्या कोनात फिरेल?"या काळात ते दोन पूर्ण क्रांती पूर्ण करेल, आणि एका क्रांतीमध्ये ती उत्तीर्ण होईल, म्हणजे. एका दिवसात ते वळेल. जसे आपण पाहू शकता, अशा मूल्यांचा एक अतिशय व्यावहारिक अर्थ आहे. रोटेशनची दिशा दर्शविण्यासाठी कोन चिन्हे वापरली जातात - एक दिशा सकारात्मक कोनांनी मोजली जाते आणि दुसरी नकारात्मक कोनांनी मोजली जाते. त्रिकोणमितीय वर्तुळात हे कसे लक्षात घेतले जाऊ शकते?
अशा कोन असलेल्या वर्तुळावर ते खालीलप्रमाणे कार्य करतात:
1) पेक्षा मोठे असलेले कोन घड्याळाच्या उलट दिशेने प्लॉट केले जातात, आवश्यक तितक्या वेळा उगमस्थानातून जातात. उदाहरणार्थ, एक कोन तयार करण्यासाठी तुम्हाला दोन पूर्ण आवर्तन आणि दुसऱ्यामधून जावे लागेल. सर्व त्रिकोणमितीय कार्ये अंतिम स्थितीसाठी मोजली जातात. हे पाहणे सोपे आहे की सर्व त्रिकोणमितीय फंक्शन्ससाठी आणि साठीची मूल्ये समान असतील.
2) नकारात्मक कोन केवळ घड्याळाच्या दिशेने, सकारात्मक कोनांच्या समान तत्त्वानुसार अचूकपणे मांडले जातात.
फक्त मोठे कोन तयार करण्याच्या पद्धतीद्वारे, आपण असा निष्कर्ष काढू शकतो की भिन्न असलेल्या कोनांच्या साइन्स आणि कोसाइनची मूल्ये समान आहेत. जर आपण स्पर्शिका आणि कोटॅन्जंट्सच्या मूल्यांचे विश्लेषण केले, तर ते भिन्न कोनांसाठी समान असतील.
अशा किमान शून्य नसलेल्या संख्या, वितर्कात जोडल्यावर, फंक्शनचे मूल्य बदलत नाही, असे म्हणतात. कालावधीहे कार्य.
अशा प्रकारे, कालावधीसाइन आणि कोसाइन समान आहेत, आणि स्पर्शिका आणि कोटँजेंट. याचा अर्थ असा की तुम्ही विचाराधीन कोनातून हे पूर्णविराम कितीही जोडले किंवा वजा केले तरी त्रिकोणमितीय फंक्शन्सची मूल्ये बदलणार नाहीत.
उदाहरणार्थ, , आणि इ.
त्रिकोणमितीय फंक्शन्सच्या या गुणधर्माच्या अधिक तपशीलवार स्पष्टीकरण आणि अनुप्रयोगाकडे आम्ही नंतर परत येऊ.
एकाच युक्तिवादाच्या त्रिकोणमितीय फंक्शन्समध्ये काही संबंध आहेत जे बर्याचदा वापरले जातात आणि म्हणतात मूलभूत त्रिकोणमितीय ओळख.
ते यासारखे दिसतात:
1)
![]() , तथाकथित "त्रिकोणमितीय एकक"
, तथाकथित "त्रिकोणमितीय एकक"
3)
![]()
4)
![]()
5)
![]()
लक्षात घ्या की, उदाहरणार्थ, नोटेशनचा अर्थ असा आहे की संपूर्ण त्रिकोणमितीय कार्य स्क्वेअर केलेले आहे. त्या. ते या फॉर्ममध्ये दर्शविले जाऊ शकते: ![]() . हे समजून घेणे महत्त्वाचे आहे की हे नोटेशनच्या बरोबरीचे नाही जसे की, या प्रकरणात केवळ युक्तिवाद स्क्वेअर केला जातो आणि संपूर्ण फंक्शन नाही, आणि याशिवाय, या प्रकारच्या अभिव्यक्ती अत्यंत दुर्मिळ आहेत.
. हे समजून घेणे महत्त्वाचे आहे की हे नोटेशनच्या बरोबरीचे नाही जसे की, या प्रकरणात केवळ युक्तिवाद स्क्वेअर केला जातो आणि संपूर्ण फंक्शन नाही, आणि याशिवाय, या प्रकारच्या अभिव्यक्ती अत्यंत दुर्मिळ आहेत.
पहिल्या ओळखीपासून दोन अतिशय उपयुक्त परिणाम आहेत जे अनेक प्रकारच्या समस्या सोडवण्यासाठी उपयुक्त ठरू शकतात. साध्या परिवर्तनानंतर, तुम्ही त्याच कोनाच्या कोसाइनद्वारे साइन व्यक्त करू शकता आणि त्याउलट:
![]()
![]()
दोन संभाव्य अभिव्यक्ती चिन्हे दिसतात कारण अंकगणित वर्गमूळ घेतल्यास केवळ नकारात्मक मूल्ये मिळतात, आणि साइन आणि कोसाइन, जसे आपण आधीच पाहिले आहे, नकारात्मक मूल्ये असू शकतात. शिवाय, त्रिकोणमितीय वर्तुळ वापरून या फंक्शन्सची चिन्हे निश्चित करणे सर्वात सोयीचे आहे, त्यामध्ये कोणते कोन आहेत यावर अवलंबून.
आता लक्षात ठेवा की कोन दोन प्रकारे मोजले जाऊ शकतात: अंश आणि रेडियनमध्ये. एक अंश आणि एक रेडियनची व्याख्या दर्शवू.
एक पदवी- हा दोन त्रिज्यांद्वारे तयार केलेला कोन आहे जो वर्तुळाच्या बरोबरीचा चाप कमी करतो.
एक रेडियन- हा त्रिज्या समान लांबीच्या कमानाने जोडलेल्या दोन त्रिज्यांद्वारे तयार केलेला कोन आहे.
त्या. ते कोन मोजण्याचे दोन भिन्न मार्ग आहेत जे पूर्णपणे समान आहेत. त्रिकोणमितीय फंक्शन्सद्वारे वैशिष्ट्यीकृत भौतिक प्रक्रियांचे वर्णन करताना, कोनांचे रेडियन माप वापरण्याची प्रथा आहे, म्हणून आपल्याला त्याची देखील सवय करावी लागेल.
पाईच्या अपूर्णांकांमध्ये रेडियनमधील कोन मोजण्याची प्रथा आहे, उदाहरणार्थ, किंवा. या प्रकरणात, "pi" क्रमांकाचे मूल्य, जे 3.14 च्या बरोबरीचे आहे, बदलले जाऊ शकते, परंतु हे क्वचितच केले जाते.
कोनांचे अंश माप रेडियनमध्ये रूपांतरित करण्यासाठीकोन आहे या वस्तुस्थितीचा फायदा घ्या, ज्यावरून सामान्य भाषांतर सूत्र प्राप्त करणे सोपे आहे:
![]()
उदाहरणार्थ, रेडियनमध्ये रूपांतरित करू: ![]() .
.
याच्या उलटही आहे सुत्ररेडियनमधून अंशांमध्ये रूपांतरण:
![]()
उदाहरणार्थ, डिग्री मध्ये रूपांतरित करू: ![]() .
.
या विषयात आपण कोनाचे रेडियन माप बरेचदा वापरणार आहोत.
विविध कोनांच्या त्रिकोणमितीय फंक्शन्सद्वारे कोणती विशिष्ट मूल्ये दिली जाऊ शकतात हे लक्षात ठेवण्याची ही वेळ आहे. काही कोनांसाठी जे गुणाकार आहेत, तेथे आहे त्रिकोणमितीय कार्यांच्या मूल्यांची सारणी. सोयीसाठी, कोन अंश आणि रेडियन मापांमध्ये दिले आहेत.

हे कोन बऱ्याचदा अनेक समस्यांना सामोरे जातात आणि या टेबलमध्ये आत्मविश्वासाने नेव्हिगेट करण्यास सक्षम असणे उचित आहे. काही कोनांच्या स्पर्शिका आणि कोटँजंट मूल्यांना अर्थ नाही, जे टेबलमध्ये डॅश म्हणून सूचित केले आहे. हे असे का आहे याचा स्वतःसाठी विचार करा किंवा धड्याच्या इन्सर्टमध्ये त्याबद्दल अधिक तपशीलवार वाचा.
आपल्या पहिल्या त्रिकोणमितीच्या धड्यात आपल्याला परिचित होण्याची शेवटची गोष्ट आहे तथाकथित घट सूत्रे वापरून त्रिकोणमितीय कार्यांचे परिवर्तन.
असे दिसून आले की त्रिकोणमितीय कार्यांसाठी एक विशिष्ट प्रकारची अभिव्यक्ती आहे जी अगदी सामान्य आणि सोयीस्करपणे सरलीकृत आहे. उदाहरणार्थ, हे अभिव्यक्ती आहेत: इ.
त्या. आम्ही अशा फंक्शन्सबद्दल बोलू जे वितर्क म्हणून एक अनियंत्रित कोन घेतात, पूर्ण किंवा अर्ध्या भागात बदलतात. अशी फंक्शन्स एका युक्तिवादासाठी सरलीकृत केली जातात जी भागांच्या बेरीज किंवा वजाबाकीच्या अनियंत्रित कोनाइतकी असते. उदाहरणार्थ, ![]() , ए
, ए ![]() . तुम्ही बघू शकता, परिणाम विरुद्ध फंक्शन असू शकतो आणि फंक्शन चिन्ह बदलू शकते.
. तुम्ही बघू शकता, परिणाम विरुद्ध फंक्शन असू शकतो आणि फंक्शन चिन्ह बदलू शकते.
म्हणून, अशा फंक्शन्सचे रूपांतर करण्याचे नियम दोन टप्प्यात विभागले जाऊ शकतात. प्रथम, आपल्याला परिवर्तनानंतर कोणते कार्य मिळेल हे निर्धारित करणे आवश्यक आहे:
1) अनियंत्रित युक्तिवाद पूर्णांकात बदलल्यास, फंक्शन बदलत नाही. हे प्रकाराच्या फंक्शन्ससाठी खरे आहे, जेथे कोणतेही पूर्णांक;
एकेकाळी शाळेत त्रिकोणमितीच्या अभ्यासासाठी वेगळा अभ्यासक्रम असायचा. प्रमाणपत्रामध्ये तीन गणितीय विषयांमध्ये ग्रेड समाविष्ट होते: बीजगणित, भूमिती आणि त्रिकोणमिती.
त्यानंतर, शालेय शिक्षण सुधारणेचा भाग म्हणून, त्रिकोणमिती हा स्वतंत्र विषय म्हणून अस्तित्वात नाही. आधुनिक शाळेत, त्रिकोणमितीची पहिली ओळख 8 व्या वर्गाच्या भूमिती अभ्यासक्रमात होते. 10 व्या वर्गातील बीजगणित अभ्यासक्रमात या विषयाचा अधिक सखोल अभ्यास सुरू आहे.
सायन, कोसाइन, टॅन्जेंट आणि कोटँजेंटच्या व्याख्या प्रथम भूमितीमध्ये काटकोन त्रिकोणाच्या बाजूंच्या संबंधांद्वारे दिल्या जातात.
काटकोन त्रिकोणातील तीव्र कोन हे कर्णाच्या विरुद्ध बाजूचे गुणोत्तर असते.
कोसाइनकाटकोन त्रिकोणातील तीव्र कोन हे कर्णाच्या समीप पायाचे गुणोत्तर असते.
स्पर्शिकाकाटकोन त्रिकोणातील तीव्र कोन हे समीप बाजूच्या विरुद्ध बाजूचे गुणोत्तर असते.
कोटँजेंटकाटकोन त्रिकोणातील तीव्र कोन हे समीप बाजूचे विरुद्ध बाजूचे गुणोत्तर असते.
या व्याख्या फक्त तीव्र कोनांवर लागू होतात (0º ते 90°).
उदाहरणार्थ,
ABC त्रिकोणामध्ये, जेथे ∠C=90°, BC हा कोन A च्या विरुद्ध असलेला पाय आहे, AC हा कोन A ला लागून असलेला पाय आहे, AB कर्ण आहे.

![]()
10 व्या वर्गाचा बीजगणित अभ्यासक्रम कोणत्याही कोनासाठी (ऋणांसह) साइन, कोसाइन, स्पर्शिका आणि कोटँजेंटच्या व्याख्या सादर करतो.
मूळ - बिंदू O(0;0) वर केंद्र असलेले त्रिज्या R चे वर्तुळ विचारात घ्या. P 0 असे abscissa अक्षाच्या सकारात्मक दिशेसह वर्तुळाच्या छेदनबिंदूचा बिंदू दर्शवू.
भूमितीमध्ये, कोन दोन किरणांनी बांधलेल्या विमानाचा भाग मानला जातो. या व्याख्येसह, कोन 0° ते 180° पर्यंत बदलतो.
त्रिकोणमितीमध्ये, कोन हा प्रारंभिक बिंदू O भोवती OP 0 किरणाच्या फिरण्याच्या परिणामाचा मानला जातो.
त्याच वेळी, ट्रॅव्हर्सलची सकारात्मक दिशा म्हणून बीमला घड्याळाच्या उलट दिशेने वळवण्याचा आणि घड्याळाच्या दिशेने नकारात्मक (हा करार पृथ्वीभोवती सूर्याच्या वास्तविक हालचालीशी संबंधित आहे) म्हणून विचार करण्यास सहमती दर्शविली.
उदाहरणार्थ, जेव्हा किरण OP 0 हा बिंदू O भोवती घड्याळाच्या उलट दिशेने कोनात फिरवला जातो तेव्हा बिंदू P 0 हा बिंदू P α वर जाईल.
कोनाने α घड्याळाच्या दिशेने वळताना - F बिंदूकडे.
या व्याख्येसह, कोन कोणतेही मूल्य घेऊ शकते.
α°+360°, α°+360°·2,...,α°+360°·n, जेथे n पूर्णांक आहे (n∈ Ζ), पुन्हा P α बिंदूकडे जाऊ या:

कोन अंश आणि रेडियनमध्ये मोजले जातात.
1° हा विकसित कोनाच्या अंश मापाच्या 1/180 च्या बरोबरीचा कोन आहे.
1 रेडियन हा मध्य कोन आहे ज्याची चाप लांबी वर्तुळाच्या त्रिज्याएवढी आहे:
∠AOB=1 rad.
![]()
![]()
रेडियन चिन्हे सहसा लिहिली जात नाहीत. पदवी पदनाम रेकॉर्डमधून वगळले जाऊ शकत नाही.
उदाहरणार्थ,
बिंदू P α, बिंदू P 0 वरून किरण OP 0 भोवती बिंदू O भोवती कोन α विरुद्ध घड्याळाच्या दिशेने फिरवून मिळवलेला, त्यात P α (x;y) समन्वय असतो.
P α बिंदू पासून abscissa अक्षावर लंब P α A सोडू.

काटकोन त्रिकोणात OP α A:
P α A - कोन α च्या विरुद्ध असलेला पाय,
OA - कोनालगतचा पाय α,
OP α कर्ण आहे.
P α A=y, OA=x, OP α =R.
काटकोन त्रिकोणातील साइन, कोसाइन, स्पर्शिका आणि कोटँजेंटच्या व्याख्येनुसार आपल्याकडे आहे:
![]()
![]()
अशाप्रकारे, अनियंत्रित त्रिज्याच्या उत्पत्तीवर केंद्र असलेल्या वर्तुळाच्या बाबतीत साइनकोन α हे बिंदू P α च्या बिंदूचे त्रिज्येच्या लांबीचे गुणोत्तर आहे.
कोसाइनकोन α हे बिंदू P α च्या abscissa आणि त्रिज्येच्या लांबीचे गुणोत्तर आहे.
स्पर्शिकाकोन α हे बिंदू P α च्या बिंदूचे त्याच्या ऍब्सिसिसा चे गुणोत्तर आहे.
कोटँजेंटकोन α हे बिंदू P α च्या abscissa आणि त्याच्या ordinate चे गुणोत्तर आहे.
 साइन, कोसाइन, स्पर्शिका आणि कोटॅन्जंटची मूल्ये केवळ α च्या मूल्यावर अवलंबून असतात आणि त्रिज्या R च्या लांबीवर अवलंबून नसतात (हे वर्तुळांच्या समानतेवरून येते).
साइन, कोसाइन, स्पर्शिका आणि कोटॅन्जंटची मूल्ये केवळ α च्या मूल्यावर अवलंबून असतात आणि त्रिज्या R च्या लांबीवर अवलंबून नसतात (हे वर्तुळांच्या समानतेवरून येते).
म्हणून, R=1 निवडणे सोयीचे आहे.
मूळ आणि त्रिज्या R=1 केंद्र असलेल्या वर्तुळाला एकक वर्तुळ म्हणतात.
व्याख्या
1) सायनसकोन α ला एकक वर्तुळाच्या P α (x;y) बिंदूचे ऑर्डिनेट म्हणतात:
2) कोसाइनकोन α ला एकक वर्तुळाच्या P α (x;y) बिंदूचा abscissa म्हणतात:
3) स्पर्शिकाकोन α हे बिंदू P α (x;y) च्या ऑर्डिनेटचे त्याच्या abscissa चे गुणोत्तर आहे, म्हणजेच sinα आणि cosα चे गुणोत्तर (जेथे cosα≠0):
4) कोटँजेंटकोन α हे बिंदू P α (x;y) च्या abscissa चे त्याच्या ऑर्डिनेटचे गुणोत्तर आहे, म्हणजेच cosα ते sinα (जेथे sinα≠0 आहे):
![]()
अशाप्रकारे मांडलेल्या व्याख्या आपल्याला कोनांची त्रिकोणमितीय फंक्शन्सच नव्हे तर संख्यात्मक वितर्कांची त्रिकोणमितीय फंक्शन्स देखील विचारात घेण्यास अनुमती देतात (जर आपण sinα, cosα, tanα आणि ctgα α रेडियन्समधील कोनाची संबंधित त्रिकोणमितीय कार्ये मानतो, म्हणजे, α संख्येचा साइन हा α रेडियनमधील कोनाचा साइन आहे, α संख्येचा कोसाइन α रेडियन्समधील कोनाचा कोसाइन आहे, इ.).
ग्रेड 10 किंवा 11 मधील बीजगणित अभ्यासक्रमात त्रिकोणमितीय फंक्शन्सच्या गुणधर्मांचा एक स्वतंत्र विषय म्हणून अभ्यास केला जातो. त्रिकोणमितीय कार्ये भौतिकशास्त्रात मोठ्या प्रमाणावर वापरली जातात.
वर्ग: |साइन, कोसाइन, स्पर्शिका - हायस्कूलच्या विद्यार्थ्यांच्या उपस्थितीत या शब्दांचा उच्चार करताना, आपण खात्री बाळगू शकता की त्यापैकी दोन तृतीयांश पुढील संभाषणात रस गमावतील. याचे कारण हे आहे की शाळेत त्रिकोणमितीची मूलतत्त्वे वास्तवापासून पूर्णपणे अलिप्तपणे शिकवली जातात आणि त्यामुळे विद्यार्थ्यांना सूत्रे आणि प्रमेयांचा अभ्यास करण्यात महत्त्वाचा मुद्दा दिसत नाही.
खरं तर, जवळून परीक्षण केल्यावर, ज्ञानाचे हे क्षेत्र अतिशय मनोरंजक असल्याचे दिसून येते, तसेच लागू केले जाते - त्रिकोणमिती खगोलशास्त्र, बांधकाम, भौतिकशास्त्र, संगीत आणि इतर अनेक क्षेत्रांमध्ये वापरली जाते.
चला मूलभूत संकल्पनांशी परिचित होऊ या आणि गणित विज्ञानाच्या या शाखेचा अभ्यास करण्यासाठी अनेक कारणे सांगू.
कथा
मानवतेने कोणत्या वेळी भविष्यातील त्रिकोणमिती सुरवातीपासून तयार करण्यास सुरुवात केली हे अज्ञात आहे. तथापि, हे दस्तऐवजीकरण आहे की बीसीच्या दुसर्या सहस्राब्दीमध्ये, इजिप्शियन लोक या विज्ञानाच्या मूलभूत गोष्टींशी परिचित होते: पुरातत्वशास्त्रज्ञांना एका कार्यासह एक पॅपिरस सापडला ज्यामध्ये दोन ज्ञात बाजूंवर पिरॅमिडच्या झुकावचा कोन शोधणे आवश्यक होते.
प्राचीन बॅबिलोनच्या शास्त्रज्ञांनी अधिक गंभीर यश मिळवले. शतकानुशतके, खगोलशास्त्राचा अभ्यास करून, त्यांनी अनेक प्रमेयांमध्ये प्रभुत्व मिळवले, कोन मोजण्यासाठी विशेष पद्धती सादर केल्या, ज्या आज आपण वापरतो: अंश, मिनिटे आणि सेकंद हे ग्रीको-रोमन संस्कृतीत युरोपियन विज्ञानाने घेतले होते, ज्यामध्ये ही युनिट्स बॅबिलोनियन्समधून आली.
असे मानले जाते की त्रिकोणमितीच्या मूलभूत गोष्टींशी संबंधित प्रसिद्ध पायथागोरियन प्रमेय, जवळजवळ चार हजार वर्षांपूर्वी बॅबिलोनियन लोकांना माहित होते.
नाव
शब्दशः, "त्रिकोणमिति" या शब्दाचे भाषांतर "त्रिकोणांचे मोजमाप" असे केले जाऊ शकते. अनेक शतकांपासून विज्ञानाच्या या विभागातील अभ्यासाचा मुख्य उद्देश काटकोन त्रिकोण होता, किंवा अधिक तंतोतंत, कोनांचे परिमाण आणि त्याच्या बाजूंच्या लांबी यांच्यातील संबंध (आज, या विभागापासून त्रिकोणमितीचा अभ्यास सुरू होतो) . जीवनात अनेकदा अशी परिस्थिती असते जेव्हा ऑब्जेक्टचे सर्व आवश्यक पॅरामीटर्स (किंवा ऑब्जेक्टचे अंतर) मोजणे व्यावहारिकदृष्ट्या अशक्य असते आणि नंतर गणनेद्वारे गहाळ डेटा प्राप्त करणे आवश्यक होते.
उदाहरणार्थ, भूतकाळात, लोक अंतराळातील वस्तूंचे अंतर मोजू शकत नव्हते, परंतु या अंतरांची गणना करण्याचा प्रयत्न आपल्या युगाच्या आगमनापूर्वी झाला होता. नेव्हिगेशनमध्ये त्रिकोणमितीने देखील महत्त्वपूर्ण भूमिका बजावली: काही ज्ञानासह, कॅप्टन नेहमी रात्री ताऱ्यांद्वारे नेव्हिगेट करू शकतो आणि अभ्यासक्रम समायोजित करू शकतो.
मूलभूत संकल्पना
सुरवातीपासून त्रिकोणमितीवर प्रभुत्व मिळवण्यासाठी अनेक मूलभूत संज्ञा समजून घेणे आणि लक्षात ठेवणे आवश्यक आहे.

एका विशिष्ट कोनाचे साइन हे कर्णाच्या विरुद्ध बाजूचे गुणोत्तर असते. आपण हे स्पष्ट करूया की विरुद्ध पाय म्हणजे आपण ज्या कोनाचा विचार करत आहोत त्याच्या विरुद्ध असलेली बाजू आहे. अशा प्रकारे, जर कोन 30 अंश असेल, तर या कोनाचा साइन नेहमी, त्रिकोणाच्या कोणत्याही आकारासाठी, ½ असेल. कोनाचा कोसाइन म्हणजे कर्णाच्या समीप पायाचे गुणोत्तर.
स्पर्शिका म्हणजे विरुद्ध बाजूचे समीप बाजूचे गुणोत्तर (किंवा, जे समान आहे, साइन ते कोसाइनचे गुणोत्तर). कोटँजेंट हे स्पर्शिकेने भागलेले एकक आहे.
प्रसिद्ध क्रमांक Pi (3.14...), जो एका युनिटच्या त्रिज्या असलेल्या वर्तुळाच्या अर्ध्या लांबीचा आहे.
लोकप्रिय चुका
सुरवातीपासून त्रिकोणमिती शिकणारे लोक अनेक चुका करतात - मुख्यतः दुर्लक्षामुळे.
प्रथम, भूमिती समस्या सोडवताना, आपण हे लक्षात ठेवले पाहिजे की साइन्स आणि कोसाइनचा वापर फक्त काटकोन त्रिकोणामध्येच शक्य आहे. असे घडते की विद्यार्थ्याने त्रिकोणाची सर्वात लांब बाजू कर्ण म्हणून “स्वयंचलितपणे” घेतली आणि त्याला चुकीचे गणना परिणाम प्राप्त होतात.

दुसरे म्हणजे, प्रथम निवडलेल्या कोनासाठी साइन आणि कोसाइनची मूल्ये गोंधळात टाकणे सोपे आहे: लक्षात ठेवा की 30 अंशांची साइन संख्यात्मकदृष्ट्या 60 च्या कोसाइनच्या समान आहे आणि त्याउलट. तुम्ही चुकीची संख्या बदलल्यास, पुढील सर्व गणिते चुकीची असतील.
तिसरे म्हणजे, समस्येचे पूर्णपणे निराकरण होईपर्यंत, तुम्ही कोणत्याही मूल्यांना गोलाकार करू नये, मूळ काढू नये किंवा दशांश म्हणून सामान्य अपूर्णांक लिहू नये. बहुतेकदा विद्यार्थी त्रिकोणमितीच्या समस्येमध्ये "सुंदर" संख्या मिळविण्याचा प्रयत्न करतात आणि लगेच तीनचे मूळ काढतात, जरी एका क्रियेनंतर हे मूळ कमी केले जाऊ शकते.
"साइन" शब्दाची व्युत्पत्ती
"साइन" शब्दाचा इतिहास खरोखरच असामान्य आहे. वस्तुस्थिती अशी आहे की लॅटिनमधून या शब्दाचे शाब्दिक भाषांतर म्हणजे "पोकळ." याचे कारण असे की एका भाषेतून दुसऱ्या भाषेत भाषांतर करताना शब्दाची योग्य समज हरवली होती.
मूळ त्रिकोणमितीय फंक्शन्सची नावे भारतातून उद्भवली आहेत, जिथे साइन ही संकल्पना संस्कृतमधील "स्ट्रिंग" या शब्दाद्वारे दर्शविली गेली होती - वस्तुस्थिती अशी आहे की तो ज्या वर्तुळावर विसावला होता त्या वर्तुळाच्या कमानीसह तो भाग धनुष्यासारखा दिसत होता. . अरब सभ्यतेच्या उत्कर्षाच्या काळात, त्रिकोणमितीच्या क्षेत्रातील भारतीय कामगिरी उधार घेण्यात आल्या आणि हा शब्द लिप्यंतरण म्हणून अरबी भाषेत गेला. असे घडले की या भाषेत आधीच उदासीनता दर्शविणारा एक समान शब्द होता आणि जर अरबांना मूळ आणि उधार घेतलेल्या शब्दातील ध्वन्यात्मक फरक समजला असेल, तर युरोपियन लोकांनी, वैज्ञानिक ग्रंथांचे लॅटिनमध्ये भाषांतर केले, चुकून अरबी शब्दाचे अक्षरशः भाषांतर केले, ज्यात काहीही नव्हते. sine च्या संकल्पनेशी करा . आम्ही आजही त्याचा वापर करतो.
मूल्यांची सारणी
सर्व संभाव्य कोनांच्या सायन्स, कोसाइन आणि स्पर्शिकेसाठी संख्यात्मक मूल्ये असलेली सारणी आहेत. खाली आम्ही 0, 30, 45, 60 आणि 90 अंशांच्या कोनांसाठी डेटा सादर करतो, जो "डमी" साठी त्रिकोणमितीचा अनिवार्य विभाग म्हणून शिकला पाहिजे, ते लक्षात ठेवणे खूप सोपे आहे;

जर असे घडले की कोनाच्या साइन किंवा कोसाइनचे संख्यात्मक मूल्य “तुमच्या डोक्यातून निघून गेले”, तर ते स्वतः मिळवण्याचा एक मार्ग आहे.
भौमितिक प्रतिनिधित्व
चला एक वर्तुळ काढू आणि त्याच्या मध्यभागी abscissa आणि ordinate अक्ष काढू. abscissa अक्ष क्षैतिज आहे, ordinate अक्ष अनुलंब आहे. ते सहसा अनुक्रमे "X" आणि "Y" म्हणून स्वाक्षरी करतात. आता आपण वर्तुळाच्या मध्यभागी एक सरळ रेषा काढू जेणेकरून आपल्याला आवश्यक असलेला कोन तो आणि X अक्षाच्या दरम्यान मिळेल. शेवटी, ज्या बिंदूपासून सरळ रेषा वर्तुळाला छेदते, तिथून आपण X अक्षावर लंब टाकतो.

जर तुम्ही आवश्यक मूल्य विसरलात, उदाहरणार्थ, परीक्षेदरम्यान आणि तुमच्याकडे त्रिकोणमितीचे पाठ्यपुस्तक नसेल तर ही पद्धत अतिशय सुसंगत आहे. तुम्हाला अशा प्रकारे अचूक संख्या मिळणार नाही, परंतु तुम्हाला निश्चितपणे ½ आणि 1.73/2 (३० अंशांच्या कोनाचे साइन आणि कोसाइन) मधील फरक दिसेल.
अर्ज
त्रिकोणमिती वापरणारे काही पहिले तज्ञ खलाशी होते ज्यांच्या डोक्यावरच्या आकाशाशिवाय उंच समुद्रावर दुसरा संदर्भ बिंदू नव्हता. आज, जहाजांचे कर्णधार (विमान आणि वाहतुकीच्या इतर पद्धती) तारे वापरून सर्वात लहान मार्ग शोधत नाहीत, परंतु सक्रियपणे जीपीएस नेव्हिगेशनचा अवलंब करतात, जे त्रिकोणमिती वापरल्याशिवाय अशक्य आहे.
भौतिकशास्त्राच्या जवळजवळ प्रत्येक विभागात तुम्हाला सायन्स आणि कोसाइन वापरून गणिते सापडतील: यांत्रिकीमधील शक्तीचा वापर असो, किनेमॅटिक्समधील वस्तूंच्या मार्गाची गणना असो, कंपन, लहरी प्रसार, प्रकाशाचे अपवर्तन - तुम्ही मूलभूत त्रिकोणमितीशिवाय करू शकत नाही. सूत्रे.
त्रिकोणमितीशिवाय अकल्पनीय असा दुसरा व्यवसाय म्हणजे सर्वेक्षक. थिओडोलाइट आणि लेव्हल किंवा अधिक जटिल उपकरण - टॅकोमीटर वापरून, हे लोक पृथ्वीच्या पृष्ठभागावरील वेगवेगळ्या बिंदूंमधील उंचीमधील फरक मोजतात.
पुनरावृत्तीक्षमता
त्रिकोणमिती केवळ त्रिकोणाच्या कोन आणि बाजूंशी संबंधित नाही, जरी तिथूनच त्याचे अस्तित्व सुरू झाले. चक्रीयता असलेल्या सर्व क्षेत्रांमध्ये (जीवशास्त्र, वैद्यकशास्त्र, भौतिकशास्त्र, संगीत इ.) तुम्हाला एक आलेख दिसेल ज्याचे नाव तुम्हाला कदाचित परिचित असेल - ती एक साइन वेव्ह आहे.

असा आलेख म्हणजे वेळेच्या अक्षावर उलगडलेले वर्तुळ आहे आणि ते लहरीसारखे दिसते. तुम्ही भौतिकशास्त्राच्या वर्गात कधी ऑसिलोस्कोपवर काम केले असेल, तर आम्ही कशाबद्दल बोलत आहोत हे तुम्हाला माहीत आहे. म्युझिक इक्वेलायझर आणि हार्ट रेट मॉनिटर दोन्ही त्यांच्या कामात त्रिकोणमिती सूत्रे वापरतात.
शेवटी
त्रिकोणमिती कशी शिकायची याचा विचार करताना, बहुतेक मध्यम आणि उच्च माध्यमिक शाळेतील विद्यार्थी ते एक कठीण आणि अव्यवहार्य विज्ञान मानू लागतात, कारण त्यांना केवळ पाठ्यपुस्तकातून कंटाळवाणा माहिती मिळते.

अव्यवहार्यतेबद्दल, आम्ही आधीच पाहिले आहे की, एक किंवा दुसर्या प्रमाणात, क्रियाकलापांच्या जवळजवळ कोणत्याही क्षेत्रात साइन्स आणि स्पर्शिका हाताळण्याची क्षमता आवश्यक असते. जडणघडणीसाठी... विचार करा: जर लोकांनी हे ज्ञान दोन हजार वर्षांपूर्वी वापरले असेल, जेव्हा एखाद्या प्रौढ व्यक्तीला आजच्या हायस्कूलच्या विद्यार्थ्यापेक्षा कमी ज्ञान होते, तर तुमच्यासाठी वैयक्तिकरित्या या विज्ञान क्षेत्राचा मूलभूत स्तरावर अभ्यास करणे वास्तववादी आहे का? समस्यांचे निराकरण करण्यासाठी काही तासांचा विचारशील सराव - आणि आपण मूलभूत अभ्यासक्रम, डमींसाठी तथाकथित त्रिकोणमितीचा अभ्यास करून आपले ध्येय साध्य कराल.