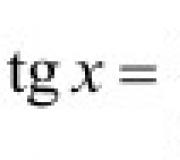बेरीजचे व्युत्पन्न कसे शोधायचे. फंक्शन्सच्या बीजगणितीय बेरीजचे व्युत्पन्न

व्युत्पन्न शोधण्याच्या ऑपरेशनला भिन्नता म्हणतात.

युक्तिवादाच्या वाढीच्या गुणोत्तराची मर्यादा म्हणून डेरिव्हेटिव्हची व्याख्या करून सर्वात सोप्या (आणि अगदी सोप्या नसलेल्या) फंक्शन्सचे डेरिव्हेटिव्ह शोधण्याच्या समस्या सोडवल्याचा परिणाम म्हणून, डेरिव्हेटिव्हची एक सारणी दिसून आली आणि नेमकी काही नियमभिन्नता आयझॅक न्यूटन (१६४३-१७२७) आणि गॉटफ्राइड विल्हेल्म लीबनिझ (१६४६-१७१६) हे व्युत्पन्न शोधण्याच्या क्षेत्रात काम करणारे पहिले होते.

म्हणून, आमच्या काळात, कोणत्याही फंक्शनचे व्युत्पन्न शोधण्यासाठी, तुम्हाला फंक्शनच्या वाढीच्या गुणोत्तराच्या वितर्काच्या वाढीच्या गुणोत्तराच्या वर नमूद केलेल्या मर्यादेची गणना करण्याची आवश्यकता नाही, परंतु तुम्हाला फक्त सारणी वापरण्याची आवश्यकता आहे. व्युत्पन्न आणि भिन्नतेचे नियम. व्युत्पन्न शोधण्यासाठी खालील अल्गोरिदम योग्य आहे.

व्युत्पन्न शोधण्यासाठी, तुम्हाला मुख्य चिन्हाखाली एक अभिव्यक्ती आवश्यक आहे साध्या फंक्शन्सचे घटकांमध्ये विभाजन कराआणि कोणती कृती निश्चित करा (उत्पादन, बेरीज, भागफल)ही कार्ये संबंधित आहेत. पुढे, आम्हाला डेरिव्हेटिव्हच्या सारणीमध्ये प्राथमिक फंक्शन्सचे डेरिव्हेटिव्ह आणि उत्पादनाच्या व्युत्पन्नांची सूत्रे, बेरीज आणि भागफल - भिन्नतेच्या नियमांमध्ये आढळतात. पहिल्या दोन उदाहरणांनंतर व्युत्पन्न सारणी आणि भिन्नता नियम दिले आहेत.

उदाहरण १.फंक्शनचे व्युत्पन्न शोधा

उपाय. भिन्नतेच्या नियमांवरून आपल्याला असे आढळून येते की फंक्शन्सच्या बेरीजची व्युत्पत्ती ही फंक्शन्सच्या डेरिव्हेटिव्हची बेरीज असते, म्हणजे.

डेरिव्हेटिव्हजच्या तक्त्यावरून आपल्याला कळते की "x" चे व्युत्पन्न एक समान आहे आणि साइनचे व्युत्पन्न कोसाइन सारखे आहे. आम्ही ही मूल्ये डेरिव्हेटिव्हच्या बेरजेमध्ये बदलतो आणि समस्येच्या स्थितीनुसार आवश्यक व्युत्पन्न शोधतो:

उदाहरण २.फंक्शनचे व्युत्पन्न शोधा

उपाय. आम्ही एका बेरजेचे व्युत्पन्न म्हणून फरक करतो ज्यामध्ये दुसऱ्या पदाचा स्थिर घटक असतो तो व्युत्पन्नाच्या चिन्हातून काढला जाऊ शकतो:

एखादी गोष्ट कोठून येते याबद्दल अजूनही प्रश्न उद्भवत असल्यास, ते सामान्यतः व्युत्पन्न सारणी आणि भिन्नतेच्या सोप्या नियमांशी परिचित झाल्यानंतर साफ केले जातात. आम्ही सध्या त्यांच्याकडे जात आहोत.

साध्या फंक्शन्सच्या व्युत्पन्नांची सारणी

1. स्थिरांक (संख्या) चे व्युत्पन्न. फंक्शन एक्सप्रेशनमधील कोणतीही संख्या (1, 2, 5, 200...) नेहमी शून्य बरोबर. हे लक्षात ठेवणे फार महत्वाचे आहे, कारण ते खूप वेळा आवश्यक असते
2. स्वतंत्र व्हेरिएबलचे व्युत्पन्न. बर्याचदा "X". नेहमी एक समान. हे बर्याच काळासाठी लक्षात ठेवणे देखील महत्त्वाचे आहे
3. पदवीचे व्युत्पन्न. समस्या सोडवताना, आपल्याला नॉन-स्क्वेअर रूट्स पॉवरमध्ये रूपांतरित करणे आवश्यक आहे.
4. पॉवर -1 च्या व्हेरिएबलचे व्युत्पन्न
5. वर्गमूळाचे व्युत्पन्न
6. साइनचे व्युत्पन्न
7. कोसाइनचे व्युत्पन्न
8. स्पर्शिकेचे व्युत्पन्न
9. कोटँजेंटचे व्युत्पन्न
10. आर्कसिनचे व्युत्पन्न
11. आर्ककोसिनचे व्युत्पन्न
12. आर्कटँजेंटचे व्युत्पन्न
13. आर्क कोटँजेंटचे व्युत्पन्न
14. नैसर्गिक लॉगरिदमचे व्युत्पन्न
15. लॉगरिदमिक फंक्शनचे व्युत्पन्न
16. घातांकाचे व्युत्पन्न
17. घातांकीय कार्याचे व्युत्पन्न

भिन्नतेचे नियम

1. बेरीज किंवा फरकाचे व्युत्पन्न
2. उत्पादनाचे व्युत्पन्न
2अ. एका स्थिर घटकाने गुणाकार केलेल्या अभिव्यक्तीचे व्युत्पन्न
3. भागफलाचे व्युत्पन्न
4. जटिल कार्याचे व्युत्पन्न

नियम १.जर कार्ये

काही ठिकाणी भिन्नता आहे, नंतर कार्ये एकाच बिंदूवर भिन्न आहेत

आणि

त्या फंक्शन्सच्या बीजगणितीय बेरीजचे व्युत्पन्न हे या फंक्शन्सच्या डेरिव्हेटिव्हच्या बीजगणितीय बेरजेइतके असते.

परिणाम. जर दोन भिन्न कार्ये स्थिर पदानुसार भिन्न असतील तर त्यांचे व्युत्पन्न समान आहेत, म्हणजे

नियम 2.जर कार्ये

काही ठिकाणी भिन्नता आहेत, नंतर त्यांचे उत्पादन त्याच बिंदूवर भिन्न आहे

आणि

त्या दोन फंक्शन्सच्या उत्पादनाचे व्युत्पन्न या प्रत्येक फंक्शनच्या उत्पादनांच्या बेरजेइतके असते आणि दुसऱ्याचे व्युत्पन्न होते.

परिणाम १. व्युत्पन्नाच्या चिन्हातून स्थिर घटक काढला जाऊ शकतो:

परिणाम २. अनेक भिन्न कार्यांच्या उत्पादनाचे व्युत्पन्न प्रत्येक घटकाच्या व इतर सर्व घटकांच्या व्युत्पन्नाच्या उत्पादनांच्या बेरजेइतके असते.

उदाहरणार्थ, तीन गुणकांसाठी:

नियम 3.जर कार्ये

काही ठिकाणी भिन्नता आणि , मग या टप्प्यावर त्यांचा भागांक देखील भिन्न आहेu/v , आणि

त्या दोन फंक्शन्सच्या भागफलाचे व्युत्पन्न अपूर्णांकाच्या बरोबरीचे असते, ज्याचा अंश हा भाजकाच्या उत्पादनांमध्ये फरक असतो आणि अंश आणि अंशाचे व्युत्पन्न आणि भाजकाचे व्युत्पन्न आणि भाजकाचा वर्ग असतो माजी अंश.

इतर पानांवर गोष्टी कुठे शोधायच्या

वास्तविक समस्यांमधील उत्पादनाचे व्युत्पन्न आणि भागफल शोधताना, एकाच वेळी अनेक भिन्नता नियम लागू करणे नेहमीच आवश्यक असते. अधिक उदाहरणेया डेरिव्हेटिव्ह्जसाठी - लेखात"उत्पादनाचे व्युत्पन्न आणि कार्यांचे भागफल".

टिप्पणी.तुम्ही एका स्थिरांकाचा (म्हणजे संख्या) बेरीजमधील संज्ञा आणि स्थिर घटक म्हणून गोंधळ करू नये! पदाच्या बाबतीत, त्याचे व्युत्पन्न शून्याच्या बरोबरीचे असते आणि स्थिर घटकाच्या बाबतीत, ते व्युत्पन्नांच्या चिन्हातून काढले जाते. या ठराविक चूक, जे वर येते प्रारंभिक टप्पाडेरिव्हेटिव्ह्जचा अभ्यास करत आहे, परंतु ते अनेक एक- आणि दोन-भाग उदाहरणे सोडवतात, सरासरी विद्यार्थी यापुढे ही चूक करत नाही.

आणि जर, उत्पादन किंवा भागांक वेगळे करताना, आपल्याकडे एक संज्ञा आहे u"v, ज्यामध्ये u- एक संख्या, उदाहरणार्थ, 2 किंवा 5, म्हणजे, एक स्थिर, नंतर या संख्येचे व्युत्पन्न शून्य समान असेल आणि म्हणून, संपूर्ण संज्ञा शून्य असेल (या प्रकरणाची उदाहरण 10 मध्ये चर्चा केली आहे).

इतर सामान्य चूक- साध्या फंक्शनचे व्युत्पन्न म्हणून जटिल फंक्शनच्या व्युत्पन्नाचे यांत्रिक समाधान. म्हणून जटिल कार्याचे व्युत्पन्नएक स्वतंत्र लेख समर्पित आहे. परंतु प्रथम आपण साध्या फंक्शन्सचे डेरिव्हेटिव्ह शोधण्यास शिकू.

वाटेत, आपण अभिव्यक्ती बदलल्याशिवाय करू शकत नाही. हे करण्यासाठी, तुम्हाला नवीन विंडोमध्ये मॅन्युअल उघडावे लागेल. शक्ती आणि मुळांसह क्रियाआणि अपूर्णांकांसह ऑपरेशन्स .

जर तुम्ही पॉवर्स आणि रूट्ससह अपूर्णांकांच्या डेरिव्हेटिव्ह्जसाठी उपाय शोधत असाल, म्हणजे, जेव्हा फंक्शन असे दिसते , नंतर "शक्ती आणि मुळांसह अपूर्णांकांची बेरीज" या धड्याचे अनुसरण करा.

आपल्याकडे एखादे कार्य असल्यास , नंतर तुम्ही "साध्या त्रिकोणमितीय फंक्शन्सचे व्युत्पन्न" हा धडा घ्याल.

चरण-दर-चरण उदाहरणे - व्युत्पन्न कसे शोधायचे

उदाहरण ३.फंक्शनचे व्युत्पन्न शोधा

उपाय. आम्ही फंक्शन एक्स्प्रेशनचे भाग परिभाषित करतो: संपूर्ण अभिव्यक्ती उत्पादनाचे प्रतिनिधित्व करते आणि त्याचे घटक बेरीज असतात, ज्याच्या दुसऱ्यामध्ये एक स्थिर घटक असतो. आम्ही उत्पादन भिन्नता नियम लागू करतो: दोन फंक्शन्सच्या उत्पादनाचे व्युत्पन्न या प्रत्येक फंक्शनच्या उत्पादनांच्या बेरजेइतके दुसऱ्याच्या व्युत्पन्नाने केले जाते:

पुढे, आम्ही बेरीजच्या भिन्नतेचा नियम लागू करतो: कार्यांच्या बीजगणितीय बेरीजचे व्युत्पन्न या फंक्शन्सच्या व्युत्पन्नांच्या बीजगणितीय बेरजेइतके असते. आमच्या बाबतीत, प्रत्येक बेरीजमध्ये दुसऱ्या टर्ममध्ये वजा चिन्ह असते. प्रत्येक बेरीजमध्ये आपण स्वतंत्र चल पाहतो, ज्याचे व्युत्पन्न एक समान असते आणि स्थिर (संख्या), ज्याचे व्युत्पन्न शून्य असते. तर, “X” एक मध्ये बदलते आणि वजा 5 शून्यात बदलते. दुसऱ्या अभिव्यक्तीमध्ये, "x" ला 2 ने गुणाकार केला जातो, म्हणून आपण "x" चे व्युत्पन्न म्हणून समान एककाने दोन गुणाकार करतो. आम्हाला खालील व्युत्पन्न मूल्ये मिळतात:

आम्ही सापडलेल्या डेरिव्हेटिव्हला उत्पादनांच्या बेरीजमध्ये बदलतो आणि समस्येच्या स्थितीनुसार आवश्यक असलेल्या संपूर्ण कार्याचे व्युत्पन्न मिळवतो:

उदाहरण ४.फंक्शनचे व्युत्पन्न शोधा

उपाय. आम्हाला भागफलाचे व्युत्पन्न शोधणे आवश्यक आहे. भाग वेगळे करण्यासाठी आम्ही सूत्र लागू करतो: दोन फंक्शन्सच्या भागाचे व्युत्पन्न अपूर्णांकाच्या बरोबरीचे असते, ज्याचा अंश हा भाजकाच्या उत्पादनांमध्ये फरक असतो आणि अंश आणि अंश आणि अंशाचे व्युत्पन्न आणि व्युत्पन्न भाजक, आणि भाजक हा पूर्वीच्या अंशाचा वर्ग आहे. आम्हाला मिळते:

आम्हाला अगोदरच उदाहरण २ मधील अंशातील घटकांचे व्युत्पन्न आढळले आहे. वर्तमान उदाहरणातील अंकातील दुसरा घटक असलेला गुणाकार वजा चिन्हाने घेतला आहे हे देखील आपण विसरू नये:

जर तुम्ही समस्यांचे निराकरण शोधत असाल ज्यामध्ये तुम्हाला फंक्शनचे व्युत्पन्न शोधणे आवश्यक आहे, जेथे मुळे आणि शक्तींचा सतत ढीग आहे, उदाहरणार्थ, , मग वर्गात स्वागत आहे "शक्ती आणि मुळांसह अपूर्णांकांच्या बेरजेचे व्युत्पन्न" .

जर तुम्हाला sine, cosines, tangents आणि इतरांच्या व्युत्पन्नांबद्दल अधिक जाणून घ्यायचे असेल तर त्रिकोणमितीय कार्ये, म्हणजे, जेव्हा फंक्शन असे दिसते , मग तुमच्यासाठी एक धडा "साध्या त्रिकोणमितीय कार्यांचे व्युत्पन्न" .

उदाहरण ५.फंक्शनचे व्युत्पन्न शोधा

उपाय. या फंक्शनमध्ये आपण उत्पादन पाहतो, त्यातील एक घटक आहे वर्गमुळस्वतंत्र व्हेरिएबलमधून, ज्याचे व्युत्पन्न आपण व्युत्पन्न सारणीमध्ये पाहिले आहे. वर्गमूळाच्या व्युत्पन्नाचे उत्पादन आणि सारणी मूल्य वेगळे करण्यासाठी नियम वापरून, आम्ही प्राप्त करतो:

उदाहरण 6.फंक्शनचे व्युत्पन्न शोधा

उपाय. या फंक्शनमध्ये आपण एक भाग पाहतो ज्याचा लाभांश हा स्वतंत्र चलचे वर्गमूळ आहे. भागांच्या भिन्नतेचा नियम वापरून, ज्याची आम्ही पुनरावृत्ती केली आणि उदाहरण 4 मध्ये लागू केले आणि वर्गमूळाच्या व्युत्पन्नाचे सारणीबद्ध मूल्य, आम्ही प्राप्त करतो:

अंशातील अपूर्णांक काढून टाकण्यासाठी, अंश आणि भाजक यांचा द्वारे गुणाकार करा.

पहिला स्तर

फंक्शनचे व्युत्पन्न. सर्वसमावेशक मार्गदर्शक (2019)

एका डोंगराळ भागातून जाणाऱ्या सरळ रस्त्याची कल्पना करू या. म्हणजेच, ते वर आणि खाली जाते, परंतु उजवीकडे किंवा डावीकडे वळत नाही. जर अक्ष रस्त्याच्या कडेने क्षैतिज दिशेने आणि अनुलंब निर्देशित केला असेल, तर रस्ता रेषा काही सतत कार्याच्या आलेखासारखी असेल:

अक्ष म्हणजे शून्य उंचीची एक विशिष्ट पातळी; जीवनात आपण समुद्र पातळीचा वापर करतो.

अशा रस्त्याने पुढे जाताना आपण वर किंवा खालीही जातो. आम्ही असेही म्हणू शकतो: जेव्हा युक्तिवाद बदलतो (ॲब्सिसा अक्षाच्या बाजूने हालचाल), फंक्शनचे मूल्य बदलते (ऑर्डिनेट अक्षाच्या बाजूने हालचाल). आता आपण विचार करूया की आपल्या रस्त्याची “खळी” कशी ठरवायची? हे कोणत्या प्रकारचे मूल्य असू शकते? हे अगदी सोपे आहे: विशिष्ट अंतर पुढे गेल्यावर उंची किती बदलेल. खरंच, रस्त्याच्या वेगवेगळ्या भागांवर, एक किलोमीटर पुढे (x-अक्षाच्या बाजूने) पुढे जात असताना, आपण वर जाऊ किंवा खाली पडू. विविध प्रमाणातसमुद्रसपाटीशी संबंधित मीटर (ऑर्डिनेट अक्षाच्या बाजूने).

चला प्रगती दर्शवू ("डेल्टा x" वाचा).

ग्रीक अक्षर (डेल्टा) हे सामान्यतः गणितामध्ये "बदल" असा उपसर्ग म्हणून वापरला जातो. म्हणजे - हे प्रमाणातील बदल आहे, - एक बदल; मग ते काय आहे? ते बरोबर आहे, परिमाणात बदल.

महत्त्वाचे: अभिव्यक्ती एक संपूर्ण, एक चल असते. “डेल्टा” ला “x” किंवा इतर कोणत्याही अक्षरापासून कधीही वेगळे करू नका! म्हणजेच, उदाहरणार्थ, .

तर, आम्ही पुढे, क्षैतिजरित्या, पुढे सरकलो आहोत. जर आपण रस्त्याच्या रेषेची तुलना फंक्शनच्या आलेखाशी केली, तर आपण उदय कसा दर्शवू? नक्कीच, . म्हणजेच जसजसे आपण पुढे जातो तसतसे आपण उंच वर जातो.

मूल्याची गणना करणे सोपे आहे: जर सुरुवातीला आपण उंचीवर होतो आणि पुढे गेल्यावर आपल्याला उंचीवर आढळले तर. जर शेवटचा बिंदू सुरुवातीच्या बिंदूपेक्षा कमी असेल तर तो नकारात्मक असेल - याचा अर्थ आपण चढत नाही तर उतरत आहोत.

चला "स्टीपनेस" कडे परत जाऊया: हे एक मूल्य आहे जे अंतराचे एक युनिट पुढे जाताना उंची किती (उंचतेने) वाढते हे दर्शवते:

आपण असे गृहीत धरू की रस्त्याच्या काही भागावर, एक किलोमीटरने पुढे गेल्यावर, रस्ता एक किलोमीटरने वर येतो. मग या ठिकाणी उतार समान आहे. आणि रस्ता, मी पुढे जात असताना, किमीने घसरला तर? मग उतार समान आहे.

आता एका टेकडीच्या माथ्यावर पाहू. तुम्ही शिखराच्या अर्धा किलोमीटर आधी विभागाची सुरुवात आणि त्यानंतर अर्धा किलोमीटरचा शेवट घेतल्यास, तुम्ही पाहू शकता की उंची जवळपास सारखीच आहे.

म्हणजेच, आमच्या तर्कानुसार, असे दिसून आले की येथे उतार जवळजवळ शून्याच्या समान आहे, जे स्पष्टपणे सत्य नाही. फक्त किलोमीटर अंतरावर बरेच काही बदलू शकते. स्टेपनेसचे अधिक पुरेसे आणि अचूक मूल्यांकन करण्यासाठी लहान क्षेत्रांचा विचार करणे आवश्यक आहे. उदाहरणार्थ, आपण एक मीटर हलवताना उंचीमधील बदल मोजल्यास, परिणाम अधिक अचूक असेल. परंतु ही अचूकता देखील आपल्यासाठी पुरेशी नसू शकते - शेवटी, जर रस्त्याच्या मधोमध एक खांब असेल तर आपण ते सहजपणे पार करू शकतो. मग आपण कोणते अंतर निवडावे? सेंटीमीटर? मिलिमीटर? कमी चांगले आहे!

IN वास्तविक जीवनजवळच्या मिलिमीटरपर्यंतचे अंतर मोजणे पुरेसे आहे. पण गणितज्ञ नेहमी परिपूर्णतेसाठी प्रयत्नशील असतात. त्यामुळे या संकल्पनेचा शोध लागला अमर्याद, म्हणजे, निरपेक्ष मूल्य हे आपण नाव देऊ शकत असलेल्या कोणत्याही संख्येपेक्षा कमी आहे. उदाहरणार्थ, तुम्ही म्हणता: एक ट्रिलियनवा! किती कमी? आणि तुम्ही या संख्येला - ने विभाजित करा आणि ते आणखी कमी होईल. वगैरे. जर आपल्याला असे लिहायचे असेल की एक परिमाण अमर्याद आहे, तर आपण असे लिहू: (आम्ही वाचतो “x शून्याकडे झुकतो”). समजून घेणं खूप गरजेचं आहे की ही संख्या शून्य नाही!पण त्याच्या अगदी जवळ. याचा अर्थ असा आहे की आपण त्यास विभाजित करू शकता.

infinitesimal च्या विरुद्ध असलेली संकल्पना infinitesimal is infinitely large (). तुम्ही असमानतेवर काम करत असताना तुम्हाला कदाचित हे आधीच कळले असेल: ही संख्या तुम्ही विचार करू शकत असलेल्या कोणत्याही संख्येपेक्षा जास्त आहे. जर तुम्ही सर्वात मोठी संख्या घेऊन आलात, तर फक्त दोनने गुणाकार करा आणि तुम्हाला आणखी मोठी संख्या मिळेल. आणि जे घडते त्याहूनही अनंत आहे. किंबहुना, अमर्याद मोठे आणि अमर्याद लहान हे एकमेकांचे व्युत्क्रम आहेत, म्हणजे at, आणि उलट: at.

आता आपण आपल्या रस्त्यावर परत जाऊया. आदर्शपणे गणना केलेला उतार हा मार्गाच्या अमर्याद विभागासाठी मोजला जाणारा उतार आहे, म्हणजे:

मी लक्षात घेतो की असीम विस्थापनासह, उंचीमधील बदल देखील अपरिमित असेल. पण मी तुम्हाला आठवण करून देतो की infinitesimal याचा अर्थ असा नाही शून्याच्या बरोबरीचे. जर तुम्ही अनंत संख्यांना एकमेकांद्वारे विभाजित केले तर तुम्हाला पूर्णपणे सामान्य संख्या मिळू शकते, उदाहरणार्थ, . म्हणजेच, एक लहान मूल्य दुसऱ्यापेक्षा कितीतरी पटीने मोठे असू शकते.

हे सर्व कशासाठी? रस्ता, खडी... आम्ही कार रॅलीला जात नाही, तर आम्ही गणित शिकवत आहोत. आणि गणितात सर्व काही अगदी सारखेच असते, फक्त वेगळे म्हटले जाते.

व्युत्पन्न संकल्पना

फंक्शनचे व्युत्पन्न म्हणजे वितर्काच्या अमर्याद वाढीसाठी फंक्शनच्या वाढीशी वितर्क वाढण्याचे गुणोत्तर.

वाढत्या प्रमाणातगणितात ते बदल म्हणतात. आर्ग्युमेंट () अक्षाच्या बाजूने फिरताना ज्या प्रमाणात बदलते त्याला म्हणतात युक्तिवाद वाढआणि अक्षाच्या बाजूने अंतराने पुढे जाताना फंक्शन (उंची) किती बदलली आहे हे निर्दिष्ट केले जाते कार्य वाढआणि नियुक्त केले आहे.

तर, फंक्शनचे व्युत्पन्न हे केव्हाचे गुणोत्तर आहे. आम्ही व्युत्पन्न फंक्शनच्या समान अक्षराने दर्शवतो, फक्त वरच्या उजवीकडे प्राइमसह: किंवा फक्त. तर, या नोटेशन्सचा वापर करून व्युत्पन्न सूत्र लिहू:

रस्त्याच्या सादृश्याप्रमाणे, येथे जेव्हा कार्य वाढते तेव्हा व्युत्पन्न सकारात्मक असते आणि जेव्हा ते कमी होते तेव्हा ते नकारात्मक असते.

व्युत्पन्न शुन्य बरोबर असणे शक्य आहे का? नक्कीच. उदाहरणार्थ, जर आपण सपाट क्षैतिज रस्त्यावर गाडी चालवत आहोत, तर खडी शून्य आहे. आणि हे खरे आहे, उंची अजिबात बदलत नाही. तर ते डेरिव्हेटिव्हसह आहे: स्थिर फंक्शनचे व्युत्पन्न (स्थिर) शून्याच्या बरोबरीचे आहे:

कारण अशा फंक्शनची वाढ कोणत्याहीसाठी शून्य असते.

टेकडीचे उदाहरण लक्षात ठेवूया. असे दिसून आले की विभागाच्या टोकांची व्यवस्था करणे शक्य आहे वेगवेगळ्या बाजूवरून, जेणेकरून टोकांची उंची समान असेल, म्हणजे, विभाग अक्षाच्या समांतर असेल:

परंतु मोठे विभाग चुकीच्या मोजमापाचे लक्षण आहेत. आपण आपला सेगमेंट स्वतःच्या समांतर वर वाढवू, नंतर त्याची लांबी कमी होईल.

अखेरीस, जेव्हा आपण शीर्षस्थानी असीम जवळ असतो, तेव्हा खंडाची लांबी अमर्याद होईल. परंतु त्याच वेळी, ते अक्षाच्या समांतर राहिले, म्हणजे, त्याच्या टोकावरील उंचीमधील फरक शून्य इतका आहे (त्याकडे कल नाही, परंतु समान आहे). तर व्युत्पन्न

हे अशा प्रकारे समजले जाऊ शकते: जेव्हा आपण अगदी शीर्षस्थानी उभे असतो तेव्हा डावीकडे किंवा उजवीकडे एक लहान शिफ्ट आपली उंची नगण्यपणे बदलते.

एक पूर्णपणे बीजगणितीय स्पष्टीकरण देखील आहे: शिरोबिंदूच्या डावीकडे कार्य वाढते आणि उजवीकडे ते कमी होते. जसे आपण आधी शोधून काढले, जेव्हा फंक्शन वाढते तेव्हा व्युत्पन्न सकारात्मक असते आणि जेव्हा ते कमी होते तेव्हा ते नकारात्मक असते. परंतु ते उडी न घेता सहजतेने बदलते (कारण रस्ता कुठेही त्याचा उतार झपाट्याने बदलत नाही). म्हणून, नकारात्मक आणि सकारात्मक मूल्यांमध्ये असणे आवश्यक आहे. हे असे असेल जेथे फंक्शन वाढणार नाही किंवा कमी होणार नाही - शिरोबिंदूवर.

कुंडसाठीही हेच खरे आहे (ज्या क्षेत्रामध्ये डावीकडील कार्य कमी होते आणि उजवीकडे वाढते):

वाढीव बद्दल थोडे अधिक.

म्हणून आम्ही युक्तिवाद परिमाणात बदलतो. आपण कोणत्या मूल्यातून बदलतो? आता त्याचा (वाद) काय झाला? आम्ही कोणताही बिंदू निवडू शकतो आणि आता आम्ही त्यातून नाचू.

समन्वयासह एक बिंदू विचारात घ्या. त्यातील फंक्शनचे मूल्य समान आहे. मग आम्ही समान वाढ करतो: आम्ही समन्वय वाढवतो. आता वाद काय? खुप सोपे: . आता फंक्शनचे मूल्य काय आहे? जेथे युक्तिवाद जातो, त्याचप्रमाणे कार्य: . फंक्शन वाढीचे काय? काहीही नवीन नाही: ही अजूनही रक्कम आहे ज्याद्वारे फंक्शन बदलले आहे:

वाढ शोधण्याचा सराव करा:

1. जेव्हा वितर्काची वाढ समान असेल तेव्हा फंक्शनची वाढ शोधा.
2. एका बिंदूवरील फंक्शनसाठीही हेच आहे.

उपाय:

IN विविध मुद्देसमान वितर्क वाढीसह, फंक्शन वाढ भिन्न असेल. याचा अर्थ असा की प्रत्येक बिंदूवरील व्युत्पन्न भिन्न आहे (आम्ही अगदी सुरुवातीलाच याबद्दल चर्चा केली - वेगवेगळ्या बिंदूंवर रस्त्याची तीव्रता वेगळी आहे). म्हणून, जेव्हा आपण व्युत्पन्न लिहितो, तेव्हा आपण कोणत्या बिंदूवर सूचित केले पाहिजे:

पॉवर फंक्शन.

पॉवर फंक्शन हे एक फंक्शन आहे जिथे वितर्क काही प्रमाणात आहे (तार्किक, बरोबर?).

शिवाय - कोणत्याही प्रमाणात: .

सर्वात सोपा केस- हे तेव्हा होते जेव्हा घातांक:

चला एका बिंदूवर त्याचे व्युत्पन्न शोधू. चला व्युत्पन्नाची व्याख्या आठवूया:

त्यामुळे युक्तिवाद वरून बदलतो. फंक्शनची वाढ काय आहे?

वाढ ही आहे. परंतु कोणत्याही टप्प्यावर फंक्शन त्याच्या वितर्क बरोबरीचे असते. म्हणून:

व्युत्पन्न समान आहे:

चे व्युत्पन्न समान आहे:

b) आता विचार करा चतुर्भुज कार्य (): .

आता ते लक्षात ठेवूया. याचा अर्थ असा की वाढीचे मूल्य दुर्लक्षित केले जाऊ शकते, कारण ते अमर्याद आहे, आणि म्हणून इतर पदाच्या पार्श्वभूमीवर नगण्य आहे:

तर, आम्ही आणखी एक नियम घेऊन आलो:

c) आम्ही तार्किक मालिका सुरू ठेवतो: .

ही अभिव्यक्ती वेगवेगळ्या प्रकारे सरलीकृत केली जाऊ शकते: बेरीजच्या घनाच्या संक्षिप्त गुणाकारासाठी सूत्र वापरून पहिला कंस उघडा किंवा घन सूत्राचा फरक वापरून संपूर्ण अभिव्यक्तीचे गुणांक बनवा. सुचविलेल्या कोणत्याही पद्धती वापरून ते स्वतः करण्याचा प्रयत्न करा.

तर, मला खालील गोष्टी मिळाल्या:

आणि पुन्हा ते लक्षात ठेवूया. याचा अर्थ असा आहे की आम्ही समाविष्ट असलेल्या सर्व अटींकडे दुर्लक्ष करू शकतो:

आम्हाला मिळते: .

ड) मोठ्या शक्तींसाठी समान नियम मिळू शकतात:

e) असे दिसून आले की हा नियम एका अनियंत्रित घातांकासह पॉवर फंक्शनसाठी सामान्यीकृत केला जाऊ शकतो, पूर्णांक देखील नाही:

नियम या शब्दात तयार केला जाऊ शकतो: "पदवी गुणांक म्हणून पुढे आणली जाते आणि नंतर कमी केली जाते."

आम्ही हा नियम नंतर सिद्ध करू (जवळजवळ अगदी शेवटी). आता काही उदाहरणे पाहू. फंक्शन्सचे व्युत्पन्न शोधा:

1. (दोन प्रकारे: सूत्राद्वारे आणि व्युत्पन्नाची व्याख्या वापरून - फंक्शनच्या वाढीची गणना करून);

1. . यावर विश्वास ठेवा किंवा नाही, हे एक पॉवर फंक्शन आहे. जर तुम्हाला प्रश्न असतील तर "हे कसे आहे? पदवी कुठे आहे?", "" हा विषय लक्षात ठेवा!
   होय, होय, मूळ देखील एक पदवी आहे, फक्त अंशात्मक: .
   याचा अर्थ असा की आपले वर्गमूळ फक्त घातांक असलेली एक शक्ती आहे:
   .
   आम्ही अलीकडे शिकलेले सूत्र वापरून व्युत्पन्न शोधतो:

   या टप्प्यावर ते पुन्हा अस्पष्ट झाल्यास, विषयाची पुनरावृत्ती करा “”!!! (ऋण घातांकासह पदवी बद्दल)

2. . आता घातांक:

   आणि आता व्याख्येद्वारे (आपण अद्याप विसरलात का?):
   ;
   .
   आता, नेहमीप्रमाणे, आम्ही समाविष्ट असलेल्या शब्दाकडे दुर्लक्ष करतो:
   .

3. . मागील प्रकरणांचे संयोजन: .

त्रिकोणमितीय कार्ये.

येथे आपण उच्च गणितातील एक तथ्य वापरू:

अभिव्यक्तीसह.

तुम्ही संस्थेच्या पहिल्या वर्षात पुरावा शिकाल (आणि तिथे जाण्यासाठी, तुम्हाला युनिफाइड स्टेट परीक्षा चांगल्या प्रकारे उत्तीर्ण होणे आवश्यक आहे). आता मी ते फक्त ग्राफिक पद्धतीने दाखवतो:

आपण पाहतो की जेव्हा फंक्शन अस्तित्वात नसते - आलेखावरील बिंदू कापला जातो. पण मूल्याच्या जवळ, फंक्शन हे "उद्दिष्ट" आहे.

याव्यतिरिक्त, तुम्ही हा नियम कॅल्क्युलेटर वापरून तपासू शकता. होय, होय, लाजू नका, कॅल्क्युलेटर घ्या, आम्ही अद्याप युनिफाइड स्टेट परीक्षेत नाही.

तर, चला प्रयत्न करूया: ;

तुमचे कॅल्क्युलेटर रेडियन मोडवर स्विच करायला विसरू नका!

इ. आम्ही पाहतो की कमी, द जवळचे मूल्यशी संबंध

अ) कार्याचा विचार करा. नेहमीप्रमाणे, त्याची वाढ शोधूया:

सायन्सचा फरक उत्पादनात बदलू. हे करण्यासाठी, आम्ही सूत्र वापरतो (विषय "" लक्षात ठेवा): .

आता व्युत्पन्न:

चला बदलूया: . मग अनंतासाठी ते देखील अनंत आहे: . साठी अभिव्यक्ती फॉर्म घेते:

आणि आता आपल्याला ते अभिव्यक्तीसह आठवते. आणि तसेच, बेरीजमध्ये (म्हणजे, येथे) असीम प्रमाण दुर्लक्षित केले जाऊ शकते तर काय?

तर, आम्हाला खालील नियम मिळतात: साइनचे व्युत्पन्न कोसाइनच्या बरोबरीचे आहे:

हे मूलभूत ("टेब्युलर") व्युत्पन्न आहेत. येथे ते एका सूचीमध्ये आहेत:

नंतर आम्ही त्यांना आणखी काही जोडू, परंतु हे सर्वात महत्वाचे आहेत, कारण ते बर्याचदा वापरले जातात.

सराव:

1. एका बिंदूवर फंक्शनचे व्युत्पन्न शोधा;
2. फंक्शनचे व्युत्पन्न शोधा.

उपाय:

1. प्रथम, मध्ये व्युत्पन्न शोधू सामान्य दृश्य, आणि नंतर त्याचे मूल्य बदला:
   ;
   .
2. येथे आपल्याकडे पॉवर फंक्शनसारखे काहीतरी आहे. चला तिला आणण्याचा प्रयत्न करूया
   सामान्य दृश्य:
   .
   छान, आता तुम्ही सूत्र वापरू शकता:
   .
   .
3. . Eeeeeee….. हे काय आहे????

ठीक आहे, तुम्ही बरोबर आहात, आम्हाला अद्याप असे डेरिव्हेटिव्ह कसे शोधायचे हे माहित नाही. येथे आपल्याकडे अनेक प्रकारच्या फंक्शन्सचे संयोजन आहे. त्यांच्यासोबत काम करण्यासाठी, तुम्हाला आणखी काही नियम शिकण्याची आवश्यकता आहे:

घातांक आणि नैसर्गिक लॉगरिदम.

गणितात एक फंक्शन आहे ज्याचे कोणत्याही मूल्याचे व्युत्पन्न एकाच वेळी फंक्शनच्या मूल्यासारखे असते. त्याला "घातांक" म्हणतात, आणि एक घातांकीय कार्य आहे

या फंक्शनचा आधार स्थिर आहे - तो अनंत आहे दशांश, म्हणजे, एक अपरिमेय संख्या (जसे की). त्याला "युलर नंबर" असे म्हणतात, म्हणूनच ते अक्षराने दर्शविले जाते.

तर, नियम:

लक्षात ठेवणे खूप सोपे आहे.

बरं, आता फार दूर जाऊ नका, उलट फंक्शनचा लगेच विचार करूया. कोणते फंक्शन घातांकीय कार्याचा व्यस्त आहे? लॉगरिदम:

आमच्या बाबतीत, आधार संख्या आहे:

अशा लॉगरिथमला (म्हणजे बेससह लॉगरिदम) "नैसर्गिक" म्हणतात आणि आम्ही त्यासाठी एक विशेष नोटेशन वापरतो: आम्ही त्याऐवजी लिहितो.

ते काय समान आहे? अर्थात, .

नैसर्गिक लॉगरिथमचे व्युत्पन्न देखील खूप सोपे आहे:

उदाहरणे:

1. फंक्शनचे व्युत्पन्न शोधा.
2. फंक्शनचे व्युत्पन्न काय आहे?

उत्तरे: प्रदर्शक आणि नैसर्गिक लॉगरिथम- डेरिव्हेटिव्ह्जच्या बाबतीत फंक्शन्स अनन्यपणे सोपे आहेत. इतर कोणत्याही बेससह घातांकीय आणि लॉगरिदमिक फंक्शन्समध्ये भिन्न व्युत्पन्न असेल, ज्याचे आम्ही नंतर विश्लेषण करू. चला नियमांचे पालन करूयाभिन्नता

भिन्नतेचे नियम

कशाचे नियम? पुन्हा नवीन पद, पुन्हा?!...

भेदव्युत्पन्न शोधण्याची प्रक्रिया आहे.

इतकंच. या प्रक्रियेला तुम्ही एका शब्दात आणखी काय म्हणू शकता? डेरिव्हेटिव्ह नाही... गणितज्ञ डिफरेंशियलला फंक्शनची समान वाढ म्हणतात. ही संज्ञा लॅटिन भिन्नता - फरक पासून आली आहे. येथे.

हे सर्व नियम काढताना, आम्ही दोन फंक्शन्स वापरू, उदाहरणार्थ, आणि. आम्हाला त्यांच्या वाढीसाठी सूत्रांची देखील आवश्यकता असेल:

एकूण 5 नियम आहेत.

व्युत्पन्न चिन्हातून स्थिरांक काढला जातो.

जर - काही स्थिर संख्या (स्थिर), नंतर.

अर्थात, हा नियम फरकासाठी देखील कार्य करतो: .

चला सिद्ध करूया. ते असू द्या, किंवा सोपे.

उदाहरणे.

फंक्शन्सचे डेरिव्हेटिव्ह शोधा:

1. एका टप्प्यावर;
2. एका टप्प्यावर;
3. एका टप्प्यावर;
4. बिंदूवर

उपाय:

1. (व्युत्पन्न सर्व बिंदूंवर समान आहे, कारण ते एक रेखीय कार्य आहे, लक्षात ठेवा?);

उत्पादनाचे व्युत्पन्न

येथे सर्व काही समान आहे: चला एक नवीन कार्य सादर करू आणि त्याची वाढ शोधू:

व्युत्पन्न:

उदाहरणे:

1. फंक्शन्सचे व्युत्पन्न शोधा आणि;
2. एका बिंदूवर फंक्शनचे व्युत्पन्न शोधा.

उपाय:

घातांकीय कार्याचे व्युत्पन्न

आता तुमचे ज्ञान कोणत्याही घातांकीय फंक्शनचे व्युत्पन्न कसे शोधायचे हे शिकण्यासाठी पुरेसे आहे, फक्त घातांकच नाही (ते काय आहे ते तुम्ही विसरला आहात का?).

तर, कुठे काही संख्या आहे.

आम्हाला फंक्शनचे डेरिव्हेटिव्ह आधीच माहित आहे, म्हणून आमचे फंक्शन नवीन बेसवर कमी करण्याचा प्रयत्न करूया:

यासाठी आपण वापरणार आहोत साधा नियम: . मग:

बरं, काम झालं. आता व्युत्पन्न शोधण्याचा प्रयत्न करा आणि हे कार्य जटिल आहे हे विसरू नका.

घडले?

येथे, स्वत: ला तपासा:

सूत्र हे घातांकाच्या व्युत्पन्नाशी अगदी सारखेच असल्याचे दिसून आले: जसे ते होते, ते तसेच राहिले, फक्त एक घटक दिसला, जो फक्त एक संख्या आहे, परंतु चल नाही.

उदाहरणे:
फंक्शन्सचे डेरिव्हेटिव्ह शोधा:

उत्तरे:

ही फक्त एक संख्या आहे जी कॅल्क्युलेटरशिवाय मोजली जाऊ शकत नाही, म्हणजेच ती आणखी लिहिता येणार नाही. साध्या स्वरूपात. म्हणून, आम्ही उत्तरात या फॉर्ममध्ये सोडतो.

लॉगरिदमिक फंक्शनचे व्युत्पन्न

हे येथे समान आहे: तुम्हाला नैसर्गिक लॉगरिथमचे व्युत्पन्न आधीच माहित आहे:

म्हणून, भिन्न बेससह अनियंत्रित लॉगरिथम शोधण्यासाठी, उदाहरणार्थ:

आपल्याला हा लॉगरिथम बेसवर कमी करणे आवश्यक आहे. तुम्ही लॉगरिदमचा आधार कसा बदलता? मला आशा आहे की तुम्हाला हे सूत्र आठवत असेल:

फक्त आता आम्ही त्याऐवजी लिहू:

भाजक हा फक्त एक स्थिरांक आहे (एक स्थिर संख्या, व्हेरिएबलशिवाय). व्युत्पन्न अगदी सोप्या पद्धतीने प्राप्त केले जाते:

घातांक आणि लॉगरिदमिक फंक्शन्सचे व्युत्पन्न युनिफाइड स्टेट परीक्षेत जवळजवळ कधीच आढळत नाहीत, परंतु ते जाणून घेणे अनावश्यक होणार नाही.

जटिल कार्याचे व्युत्पन्न.

"जटिल कार्य" म्हणजे काय? नाही, हा लॉगरिदम नाही आणि आर्कटँजंट नाही. ही फंक्शन्स समजणे कठीण असू शकते (जरी तुम्हाला लॉगरिदम अवघड वाटत असेल तर, "लोगॅरिथम" हा विषय वाचा आणि तुम्हाला बरे वाटेल), परंतु गणिताच्या दृष्टिकोनातून, "जटिल" या शब्दाचा अर्थ "कठीण" असा होत नाही.

एका लहान कन्व्हेयर बेल्टची कल्पना करा: दोन लोक बसले आहेत आणि काही वस्तूंसह काही क्रिया करत आहेत. उदाहरणार्थ, पहिला रॅपरमध्ये चॉकलेट बार गुंडाळतो आणि दुसरा रिबनने बांधतो. परिणाम एक संमिश्र वस्तू आहे: एक चॉकलेट बार गुंडाळलेला आणि रिबनने बांधलेला. चॉकलेट बार खाण्यासाठी, तुम्हाला उलटे पायऱ्या करणे आवश्यक आहे उलट क्रमात.

चला एक समान गणितीय पाइपलाइन तयार करू: प्रथम आपण एका संख्येचा कोसाइन शोधू, आणि नंतर परिणामी संख्येचा वर्ग करू. तर, आम्हाला एक क्रमांक (चॉकलेट) दिला जातो, मला त्याचा कोसाइन (रॅपर) सापडतो आणि मग मला जे मिळाले ते तुम्ही वर्ग करा (ते रिबनने बांधा). काय झालं? कार्य. हे एक उदाहरण आहे जटिल कार्य: जेव्हा, त्याचे मूल्य शोधण्यासाठी, आम्ही थेट व्हेरिएबलसह पहिली क्रिया करतो, आणि नंतर दुसरी क्रिया पहिल्यापासून काय निष्पन्न होते.

आपण समान पायऱ्या उलट क्रमाने सहजपणे करू शकतो: प्रथम आपण त्याचे वर्गीकरण करा आणि नंतर मी परिणामी संख्येचा कोसाइन शोधतो: . अंदाज लावणे सोपे आहे की परिणाम जवळजवळ नेहमीच वेगळा असेल. महत्वाचे वैशिष्ट्यजटिल कार्ये: जेव्हा क्रियांचा क्रम बदलतो तेव्हा कार्य बदलते.

दुसऱ्या शब्दात, कॉम्प्लेक्स फंक्शन हे फंक्शन आहे ज्याचा वितर्क हे दुसरे फंक्शन आहे: .

पहिल्या उदाहरणासाठी, .

दुसरे उदाहरण: (समान गोष्ट). .

आम्ही शेवटची कृती करू असे म्हटले जाईल "बाह्य" कार्य, आणि क्रिया प्रथम केली - त्यानुसार "अंतर्गत" कार्य(ही अनौपचारिक नावे आहेत, मी ती फक्त सोप्या भाषेत सामग्री स्पष्ट करण्यासाठी वापरतो).

कोणते फंक्शन बाह्य आहे आणि कोणते अंतर्गत आहे हे स्वतः ठरवण्याचा प्रयत्न करा:

उत्तरे:आतील आणि बाह्य फंक्शन्स वेगळे करणे हे व्हेरिएबल्स बदलण्यासारखेच आहे: उदाहरणार्थ, फंक्शनमध्ये

1. आपण प्रथम कोणती कृती करू? प्रथम, साइनची गणना करू, आणि त्यानंतरच ते घन करू. याचा अर्थ ते अंतर्गत कार्य आहे, परंतु बाह्य कार्य आहे.
   आणि मूळ कार्य त्यांची रचना आहे: .
2. अंतर्गत: ; बाह्य: .
   परीक्षा:.
3. अंतर्गत: ; बाह्य: .
   परीक्षा:.
4. अंतर्गत: ; बाह्य: .
   परीक्षा:.
5. अंतर्गत: ; बाह्य: .
   परीक्षा:.

आपण व्हेरिएबल्स बदलतो आणि फंक्शन मिळवतो.

बरं, आता आपण आपली चॉकलेट बार काढू आणि डेरिव्हेटिव्ह शोधू. प्रक्रिया नेहमी उलट केली जाते: प्रथम आपण बाह्य कार्याचे व्युत्पन्न शोधतो, नंतर आतील कार्याच्या व्युत्पन्नाने परिणाम गुणाकार करतो. मूळ उदाहरणाच्या संबंधात, हे असे दिसते:

दुसरे उदाहरण:

तर, शेवटी अधिकृत नियम तयार करूया:

जटिल कार्याचे व्युत्पन्न शोधण्यासाठी अल्गोरिदम:

हे सोपे दिसते, बरोबर?

चला उदाहरणांसह तपासूया:

उपाय:

1) अंतर्गत: ;

बाह्य: ;

2) अंतर्गत: ;

(आत्तापर्यंत ते कापण्याचा प्रयत्न करू नका! कोसाइनच्या खाली काहीही येत नाही, लक्षात ठेवा?)

3) अंतर्गत: ;

बाह्य: ;

हे ताबडतोब स्पष्ट होते की हे तीन-स्तरीय जटिल कार्य आहे: सर्व केल्यानंतर, हे स्वतःच एक जटिल कार्य आहे आणि आम्ही त्यातून मूळ देखील काढतो, म्हणजेच आम्ही तिसरी क्रिया करतो (आम्ही चॉकलेट ठेवतो. रॅपर आणि ब्रीफकेसमध्ये रिबनसह). परंतु घाबरण्याचे कोणतेही कारण नाही: आम्ही अजूनही हे कार्य नेहमीप्रमाणेच त्याच क्रमाने "अनपॅक" करू: शेवटपासून.

म्हणजेच, प्रथम आपण मूळ, नंतर कोसाइन आणि नंतर कंसात अभिव्यक्ती वेगळे करतो. आणि मग आपण ते सर्व गुणाकार करतो.

अशा परिस्थितीत, क्रियांची संख्या करणे सोयीस्कर आहे. म्हणजेच, आपल्याला काय माहित आहे याची कल्पना करूया. या अभिव्यक्तीच्या मूल्याची गणना करण्यासाठी आम्ही कोणत्या क्रमाने क्रिया करू? चला एक उदाहरण पाहू:

जितक्या नंतर क्रिया केली जाईल तितके संबंधित कार्य अधिक "बाह्य" असेल. क्रियांचा क्रम पूर्वीप्रमाणेच आहे:

येथे घरटे साधारणपणे 4-स्तरीय असते. चला कृतीचा मार्ग निश्चित करूया.

1. मूलगामी अभिव्यक्ती. .

2. रूट. .

3. साइन. .

4. चौरस. .

5. हे सर्व एकत्र ठेवणे:

व्युत्पन्न. मुख्य गोष्टींबद्दल थोडक्यात

फंक्शनचे व्युत्पन्न- वितर्काच्या अमर्याद वाढीसाठी फंक्शनच्या वाढीशी युक्तिवादाच्या वाढीचे गुणोत्तर:

मूलभूत व्युत्पन्न:

भिन्नतेचे नियम:

स्थिरांक व्युत्पन्न चिन्हातून काढला जातो:

बेरीजचे व्युत्पन्न:

उत्पादनाचे व्युत्पन्न:

भागाचे व्युत्पन्न:

जटिल कार्याचे व्युत्पन्न:

जटिल कार्याचे व्युत्पन्न शोधण्यासाठी अल्गोरिदम:

1. आम्ही "अंतर्गत" फंक्शन परिभाषित करतो आणि त्याचे व्युत्पन्न शोधतो.
2. आम्ही "बाह्य" फंक्शन परिभाषित करतो आणि त्याचे व्युत्पन्न शोधतो.
3. आम्ही पहिल्या आणि दुसऱ्या बिंदूंचे परिणाम गुणाकार करतो.

"उच्च गणिताचे घटक" या शैक्षणिक विषयातील परीक्षेसाठी प्रश्न

विशेष 230115 "संगणक प्रणालींमध्ये प्रोग्रामिंग" साठी

2012\2013 शैक्षणिक वर्ष.

मॅट्रिक्स आणि त्यांच्यावर ऑपरेशन्स.

(बद्दल.शून्य मॅट्रिक्स एक मॅट्रिक्स आहे ज्याचे सर्व घटक 0 च्या समान आहेत.

बद्दल.समान परिमाण mxn चे दोन मॅट्रिक्स म्हणतात समान, छेदनबिंदूवर असल्यास i-th ओळआणि एक आणि दुसऱ्या मॅट्रिक्समधील j-व्या स्तंभात समान संख्या आहे; i=1, 2, ..., m; j=1, 2, ..., n .

द्या ए= (a ij) काही मॅट्रिक्स आहे आणि g ही अनियंत्रित संख्या आहे, नंतर g ए= (g a ij), म्हणजे, जेव्हा मॅट्रिक्स A ला संख्या g ने गुणाकार केला जातो, तेव्हा मॅट्रिक्स A बनवणाऱ्या सर्व संख्यांचा g संख्येने गुणाकार केला जातो.

A आणि B हे समान परिमाण A = (a ij), B = (b ij) चे मॅट्रिक्स असू द्या, तर त्यांची बेरीज A + B ही समान परिमाणाचा मॅट्रिक्स C = (c ij) आहे, c ij सूत्रावरून निर्धारित = a ij + b ij, म्हणजे, दोन मॅट्रिक्स जोडताना, त्यांच्यामध्ये समान रीतीने असलेल्या संख्या जोड्यांमध्ये जोडल्या जातात.

मॅट्रिक्स A चा मॅट्रिक्स B ने गुणाकार केला जाऊ शकतो, म्हणजे, मॅट्रिक्स A च्या स्तंभ n ची संख्या मॅट्रिक्स B च्या पंक्तींच्या संख्येइतकी असल्यास मॅट्रिक्स C = AB आढळू शकते आणि मॅट्रिक्स C मध्ये मॅट्रिक्स A इतक्या पंक्ती असतील. पंक्ती आहेत आणि मॅट्रिक्समध्ये जितके स्तंभ B आहेत तितके स्तंभ आहेत. मॅट्रिक्स C चा प्रत्येक घटक सूत्राद्वारे परिभाषित केला जातो.

उत्पादन मॅट्रिक्स C चे घटक c ij बेरीज समानपहिल्या फॅक्टर मॅट्रिक्सच्या i-व्या पंक्तीच्या घटकांची उत्पादने आणि दुसऱ्या घटक मॅट्रिक्सच्या j-व्या स्तंभातील संबंधित घटकांची उत्पादने.

निर्धारकाची संकल्पना आणि त्याचे गुणधर्म.

या शब्दाचे इतर अर्थ आहेत, पहा निर्धारक (मूल्ये) .

निर्धारक(किंवा निर्धारक) - मूलभूत संकल्पनांपैकी एक रेखीय बीजगणित. निर्धारक मॅट्रिक्सआहे बहुपदीचौरस मॅट्रिक्सच्या घटकांमधून (म्हणजे, ज्यामध्ये पंक्ती आणि स्तंभांची संख्या समान आहे). सामान्यतः मॅट्रिक्सकोणत्याही कम्युटेटिव्हवर परिभाषित केले जाऊ शकते अंगठी, या प्रकरणात निर्धारक समान रिंगचा एक घटक असेल.

गुणधर्म 1. निर्धारकाचे मूल्य बदलणार नाही जर त्याच्या सर्व पंक्ती स्तंभांद्वारे बदलल्या गेल्या असतील आणि प्रत्येक पंक्ती समान संख्येसह स्तंभाने बदलली असेल, म्हणजे

गुणधर्म 2. निर्धारकाच्या दोन स्तंभ किंवा दोन ओळींची पुनर्रचना करणे म्हणजे त्याचा -1 ने गुणाकार करणे समतुल्य आहे.

गुणधर्म 3. जर निर्धारकाला दोन समान स्तंभ किंवा दोन समान पंक्ती असतील, तर ते शून्य आहे.

गुणधर्म 4. एका स्तंभातील सर्व घटकांचा किंवा निर्धारकाच्या एका पंक्तीचा k कोणत्याही संख्येने गुणाकार करणे हे k या संख्येने निर्धारकाचा गुणाकार करण्यासारखे आहे.

गुणधर्म 5. जर काही स्तंभ किंवा काही पंक्तीचे सर्व घटक शून्याच्या समान असतील, तर निर्धारक स्वतः शून्य असेल. ही मालमत्ता मागील एक विशेष केस आहे (k=0 साठी).

गुणधर्म 6. जर दोन स्तंभांचे किंवा निर्धारकाच्या दोन ओळींचे संबंधित घटक प्रमाणबद्ध असतील, तर निर्धारक शून्याच्या बरोबरीचा असेल.

गुणधर्म 7. जर निर्धारकाच्या nव्या स्तंभाचा किंवा nव्या पंक्तीचा प्रत्येक घटक दोन पदांची बेरीज असेल, तर निर्धारक दोन निर्धारकांची बेरीज म्हणून प्रस्तुत केला जाऊ शकतो, त्यापैकी एक nव्या स्तंभात किंवा अनुक्रमे, nव्या मध्ये पंक्तीमध्ये नमूद केलेल्या अटींपैकी पहिली आहे, आणि दुसरी - दुसरी; उर्वरित ठिकाणी उभे असलेले घटक तीन निर्धारकांच्या माइलस्टोनसाठी समान आहेत.

गुणधर्म 8. जर एखाद्या विशिष्ट स्तंभाच्या (किंवा काही पंक्ती) घटकांमध्ये आम्ही दुसऱ्या स्तंभाचे (किंवा दुसरी पंक्ती) संबंधित घटक जोडले, ज्याला कोणत्याही सामान्य घटकाने गुणाकार केला, तर निर्धारकाचे मूल्य बदलणार नाही. उदाहरणार्थ. निर्धारकांचे पुढील गुणधर्म बीजगणितीय पूरक आणि किरकोळ या संकल्पनेशी संबंधित आहेत. घटकाचा किरकोळ हा घटक ज्याच्या छेदनबिंदूवर आहे त्या पंक्ती आणि स्तंभाला ओलांडून दिलेल्या घटकातून मिळवलेला निर्धारक असतो.

निर्धारकाच्या कोणत्याही घटकाची बीजगणितीय पूरकता या घटकाच्या किरकोळ बरोबरीची असते, जर घटक स्थित असलेल्या छेदनबिंदूवरील पंक्ती आणि स्तंभाच्या संख्यांची बेरीज सम संख्या असेल तर त्याच्या चिन्हासह घेतले जाते. ही संख्या विषम असल्यास विरुद्ध चिन्ह.

आम्ही घटकाचे बीजगणितीय पूरक समान नावाच्या कॅपिटल अक्षराने आणि त्या घटकालाच दर्शविणाऱ्या अक्षराच्या समान संख्येने दर्शवू.

गुणधर्म 9. निर्धारक हा कोणत्याही स्तंभाच्या (किंवा पंक्ती) घटकांच्या बीजगणितीय पूरकांच्या बेरजेइतका असतो. दुसऱ्या शब्दांत, खालील समानता धारण करतात:

निर्धारकांची गणना.

निर्धारकांची गणना त्यांच्या ज्ञात गुणधर्मांवर आधारित आहे, जी सर्व ऑर्डरच्या निर्धारकांना लागू होते. हे गुणधर्म आहेत:

1. तुम्ही निर्धारकाच्या दोन पंक्ती (किंवा दोन स्तंभ) पुनर्रचना केल्यास, निर्धारक चिन्ह बदलेल.

2. जर निर्धारकाच्या दोन स्तंभांचे (किंवा दोन पंक्ती) संबंधित घटक समान किंवा प्रमाणात असतील, तर निर्धारक शून्य असेल.

3. जर तुम्ही पंक्ती आणि स्तंभांचा क्रम राखून त्यांची अदलाबदल केली तर निर्धारकाचे मूल्य बदलणार नाही.

4. पंक्तीच्या (किंवा स्तंभ) सर्व घटकांमध्ये समान घटक असल्यास, तो निर्धारक चिन्हातून बाहेर काढला जाऊ शकतो.

5. दुसऱ्या पंक्तीचे (किंवा स्तंभ) संबंधित घटक एकाच पंक्तीच्या (किंवा स्तंभ) घटकांमध्ये जोडल्यास, त्याच संख्येने गुणाकार केल्यास निर्धारकाचे मूल्य बदलणार नाही. थर्ड-ऑर्डर निर्धारकांसाठी, ही मालमत्ता लिहिली जाऊ शकते, उदाहरणार्थ, याप्रमाणे:

6. सूत्र वापरून द्वितीय-क्रम निर्धारकाची गणना केली जाते

7. सूत्र वापरून तृतीय-क्रम निर्धारकाची गणना केली जाते

थर्ड-ऑर्डर निर्धारकाची गणना करण्यासाठी एक सोयीस्कर योजना आहे (चित्र 1 आणि चित्र 2 पहा).

अंजीर मध्ये दर्शविलेल्या आकृतीनुसार. 1, जोडलेल्या घटकांची उत्पादने त्यांच्या स्वतःच्या चिन्हासह घेतली जातात आणि अंजीरमधील आकृतीनुसार. 2 - उलट सह. निर्धारकाचे मूल्य परिणामी सहा उत्पादनांच्या बीजगणितीय बेरजेइतके असते.

रेखीय समीकरणांची प्रणाली. मूलभूत संकल्पना आणि व्याख्या.

प्रणालीmр रेखीय बीजगणितीय समीकरणे सहn अज्ञात(किंवा, रेखीय प्रणाली, देखील वापरले संक्षेप SLAU) व्ही रेखीय बीजगणितफॉर्मच्या समीकरणांची एक प्रणाली आहे

प्रणाली रेखीय समीकरणेतीन व्हेरिएबल्समधून संच ठरवतो विमाने. छेदनबिंदू हा उपाय आहे.

येथे समीकरणांची संख्या आहे आणि अज्ञातांची संख्या आहे. x 1 , x 2 , …, x n- अज्ञात जे निर्धारित करणे आवश्यक आहे. a 11 , a 12 , …, a mn- सिस्टम गुणांक - आणि b 1 , b 2 , … b मी- मुक्त सदस्य - ज्ञात असल्याचे गृहीत धरले जाते . गुणांक निर्देशांक ( a ij) प्रणाली समीकरण संख्या दर्शवतात ( i) आणि अज्ञात ( j), ज्यावर हा गुणांक अनुक्रमे उभा आहे .

प्रणाली (1) म्हणतात एकसंध , जर त्याच्या सर्व मुक्त अटी शून्य समान असतील ( b 1 = b 2 = … = b मी= 0), अन्यथा - विषम.

प्रणाली (1) म्हणतात चौरस , संख्या असल्यास मीसंख्येच्या समान समीकरणे nअज्ञात

उपायप्रणाली (1) - संच nसंख्या c 1 , c 2 , …, c n, जसे की प्रत्येकाची बदली c iऐवजी x iप्रणालीमध्ये (1) त्याची सर्व समीकरणे मध्ये बदलते ओळख.

प्रणाली (1) म्हणतात संयुक्त , त्यात किमान एक उपाय असल्यास, आणि संयुक्त नसलेले, तिच्याकडे एकच उपाय नसेल तर.

प्रकार (1) च्या संयुक्त प्रणालीमध्ये एक किंवा अधिक उपाय असू शकतात.

उपाय c 1 (1) , c 2 (1) , …, c n(1) आणि c 1 (2) , c 2 (2) , …, c n(2) फॉर्मच्या संयुक्त प्रणाली (1) म्हणतात विविध, किमान एक समानतेचे उल्लंघन झाल्यास:

फॉर्मची संयुक्त प्रणाली (1) म्हणतात निश्चित , त्यात एक अद्वितीय उपाय असल्यास; जर त्यात किमान दोन भिन्न उपाय असतील तर त्याला म्हणतात अनिश्चित. अज्ञात पेक्षा अधिक समीकरणे असल्यास, त्याला म्हणतात पुन्हा परिभाषित .

रेखीय समीकरणांच्या प्रणाली सोडवण्याच्या पद्धती (क्रेमर आणि गॉस पद्धत).

गॉस पद्धत - क्लासिक सोल्यूशन पद्धत रेखीय बीजगणितीय समीकरणांची प्रणाली(SLAU). ही क्रमिक निर्मूलनाची पद्धत आहे चलजेव्हा, प्राथमिक परिवर्तनांचा वापर करून, समीकरणांची एक प्रणाली समतुल्य त्रिकोणी प्रणालीमध्ये कमी केली जाते, ज्यामधून शेवटच्या (संख्येनुसार) व्हेरिएबल्सपासून सुरू होणारी इतर सर्व चल क्रमाने आढळतात. .

क्रेमरची पद्धत (क्रेमरचा नियम)- चौरस सोडवण्याची पद्धत रेखीय बीजगणितीय समीकरणांची प्रणालीशून्य नसलेल्या सह निर्धारक मुख्य मॅट्रिक्स(आणि अशा समीकरणांसाठी एक अनोखा उपाय आहे). नावाने हाक मारली गॅब्रिएल क्रेमर(1704-1752), ज्याने या पद्धतीचा शोध लावला.

वेक्टर. त्यांच्यावर रेखीय ऑपरेशन्स.

वेक्टर हा एक निर्देशित विभाग आहे. जर सदिशाची सुरुवात बिंदू A वर असेल आणि शेवट B बिंदूवर असेल, तर वेक्टरला AB असे नाव दिले जाते. जर व्हेक्टरची सुरुवात आणि शेवट दर्शविला नसेल, तर ते लोअरकेस अक्षराने दर्शविले जाते लॅटिन वर्णमालाअ, ब, क,…. BA व्हेक्टर AB च्या विरुद्ध निर्देशित केलेला सदिश दर्शवतो. एक सदिश ज्याचा आरंभ आणि शेवट एकसारखा असतो त्याला शून्य म्हणतात आणि ō ने दर्शविले जाते. त्याची दिशा अनिश्चित आहे.

व्हेक्टरची लांबी किंवा मापांक म्हणजे त्याची सुरुवात आणि शेवट यामधील अंतर. रेकॉर्ड |AB| आणि |a| AB आणि a या सदिशांचे मॉड्यूल दर्शवा.

व्हेक्टर एकाच रेषेला समांतर असल्यास समरेख म्हणतात आणि समान समतलाला समांतर असल्यास कॉप्लॅनर म्हणतात.

दोन सदिश समरेषीय असतील, त्यांची दिशा समान असेल आणि त्यांची लांबी समान असेल तर त्यांना समान म्हटले जाते.

वेक्टरवरील रेखीय ऑपरेशन्समध्ये हे समाविष्ट आहे:

1) सदिशाचा संख्येने गुणाकार (एक सदिश a आणि संख्या α चे गुणाकार हा α∙a दर्शविणारा सदिश आहे. (किंवा त्याउलट a∙α), ज्याचे मॉड्यूलस |α a| =| α||a|, आणि दिशा व्हेक्टर a च्या दिशेशी एकरूप होते, जर α>0, आणि विरुद्ध असेल तर α< 0.

2) सदिश जोडणे (सदिशांची बेरीज एक सदिश आहे, द्वारे दर्शविली जाते, ज्याची सुरूवात पहिल्या वेक्टरच्या सुरूवातीस a 1 असते आणि शेवट शेवटच्या वेक्टर a n च्या शेवटी असते, तुटलेली रेषा बनलेली असते. या जोडणीच्या नियमाला खंडित रेषा बंद करण्याचा नियम म्हणतात.

सरळ रेषेवर ई दिशा दिलेली आहे, धन म्हणून घेतली जाते, त्याला ई अक्ष म्हणतात.

सदिशांचे रेखीय संयोजन a i हा एक सदिश a आहे, ज्याची सूत्राने व्याख्या केली आहे, जिथे काही संख्या आहेत.

जर n सदिश a i समानता प्रणालीसाठी

ही प्रणाली रेखीयरित्या स्वतंत्र आहे असे म्हटले तरच खरे आहे. जर समानता (1) साठी समाधानी असेल, त्यापैकी किमान एक शून्यापेक्षा भिन्न असेल, तर ai च्या सदिश प्रणालीला रेखीय अवलंबित म्हणतात. उदाहरणार्थ, त्रिमितीय अवकाशातील कोणतेही समरेखीय सदिश, तीन कॉप्लॅनर वेक्टर, चार किंवा अधिक सदिश नेहमी रेखीय अवलंबित असतात.

अंतराळातील तीन क्रमबद्ध रेखीय स्वतंत्र वेक्टर ē 1, ē 2, ē 3 यांना आधार म्हणतात. नॉन-कॉप्लॅनर वेक्टरचा क्रमबद्ध तिप्पट नेहमी आधार बनवतो. अंतराळातील कोणताही सदिश a चा आधार ē 1, ē 2, ē 3, म्हणजेच आधार सदिशांच्या रेखीय संयोजनाप्रमाणे a चे प्रतिनिधित्व करतो: a= xē 1 + yē 2 + zē 3, जेथे x, y, z ē 1, ē 2, ē 3 या आधारावर निर्देशांक वेक्टर a आहेत. आधाराला ऑर्थोनॉर्मल म्हणतात जर त्याचे वेक्टर परस्पर लंब असतील आणि एकक लांबी असेल. असा आधार i, j, k, म्हणजे i=(1, 0, 0), j=(0, 1, 0), k=(0, 0, 1) द्वारे दर्शविला जातो.

उदाहरण 5. वेक्टर ऑर्थोनॉर्मल आधारावर i, j, k निर्देशांकांद्वारे निर्दिष्ट केले जातात: a=(2;-1;8), e 1 = (1,2,3), e 2 = (1,-1,- 2), e 3 = (1,-6,0). तिहेरी e 1, e 2, e 3 एक आधार बनवतो याची खात्री करा आणि या आधारावर सदिशाचे समन्वय शोधा.

उपाय. जर निर्धारक , e 1, e 2, e 3 या सदिशांच्या समन्वयाने बनलेला, 0 च्या बरोबरीचा नसतो, तर e 1, e 2, e 3 हे सदिश रेखीयरित्या स्वतंत्र असतात आणि म्हणून, एक आधार तयार करतात. आम्ही खात्री करतो की = -18-4+3-12=-31 अशा प्रकारे, तिहेरी e 1, e 2, e 3 हा आधार आहे.

x, y, z च्या आधारे e 1, e 2, e 3 मधील सदिश a चे समन्वय दर्शवू. नंतर a = (x,y,z) = xe 1 + yе 2 + zе 3. अटीनुसार a = 2i – j +8k, e 1 = i +2j +3k, e 2 = i – j -2k, e 3 = i – 6j, नंतर समानतेवरून a = xe1 + ye 2 + zе 3 it खालील प्रमाणे, की 2i – j +8k = xi + 2xj + 3xk + yi – yj -2yk +zi -6zj = (x+y+z)i +(2x-y-6z)j +(3x-2y)k. तुम्ही बघू शकता, परिणामी समानतेच्या डाव्या बाजूचा वेक्टर उजव्या बाजूच्या वेक्टरच्या बरोबरीचा आहे आणि हे फक्त तेव्हाच शक्य आहे जेव्हा त्यांचे संबंधित निर्देशांक समान असतील. येथून आम्हाला अज्ञात x, y, z शोधण्यासाठी एक प्रणाली मिळते:

त्याचे समाधान: x = 2, y = -1, z = 1. तर, a = 2e 1 – e 2 + e 3 = (2,-1,1).

वेक्टर विघटन. वेक्टरचे डॉट उत्पादन.

स्केलर उत्पादनकधी कधी अंतर्गत उत्पादन- दोन वर शस्त्रक्रिया वेक्टर, ज्याचा परिणाम म्हणजे संख्या ( स्केलर), समन्वय प्रणालीपासून स्वतंत्र आणि घटक वेक्टरची लांबी आणि त्यांच्यामधील कोन दर्शविते. हे ऑपरेशन गुणाकाराशी संबंधित आहे लांबीवेक्टर x चालू प्रक्षेपणवेक्टर y ते वेक्टर x. हे ऑपरेशन सहसा असे मानले जाते बदलीआणि रेखीयप्रत्येक घटकासाठी.

सामान्यतः खालीलपैकी एक नोटेशन वापरले जाते:

किंवा ( पदनाम डिराक, अनेकदा वापरले क्वांटम यांत्रिकीराज्य वेक्टरसाठी):

हे सहसा गृहीत धरले जाते की स्केलर उत्पादन सकारात्मक निश्चित आहे, म्हणजे

सगळ्यांसाठी .

हे गृहित धरले नाही, तर काम म्हणतात अनिश्चित.

डॉट उत्पादनव्ही वेक्टर जागावर फील्ड जटिल(किंवा वास्तविक) संख्याघटकांच्या प्रत्येक जोडीसाठी परिभाषित केलेली (किंवा) मूल्ये घेणारे आणि खालील अटी पूर्ण करणारे घटकांचे कार्य आहे:

लक्षात घ्या की व्याख्येच्या परिच्छेद 2 वरून ते खालीलप्रमाणे आहे. म्हणून, जटिल (सामान्य बाबतीत) मूल्ये असूनही, आयटम 3 अर्थपूर्ण आहे डॉट उत्पादन.

वेक्टरचे क्रॉस उत्पादन.

वेक्टर कलाकृती- हे स्यूडोव्हेक्टर, लंबदोन घटकांपासून तयार केलेले विमान, जे परिणाम आहे बायनरी ऑपरेशन"वेक्टर गुणाकार" संपला वेक्टरतीन आयामांमध्ये युक्लिडियन जागा. कामही नाही बदली, किंवा सहयोगी(हे आहे विरोधी) आणि पेक्षा वेगळे आहे वेक्टरचे स्केलर उत्पादन. अनेक अभियांत्रिकी आणि भौतिकशास्त्राच्या समस्यांमध्ये, तुम्हाला दोन विद्यमान समस्यांशी लंब वेक्टर तयार करण्यास सक्षम असणे आवश्यक आहे - वेक्टर उत्पादन ही संधी प्रदान करते. क्रॉस उत्पादन हे सदिशांच्या लंबाचे "मापन" करण्यासाठी उपयुक्त आहे - दोन सदिशांच्या क्रॉस उत्पादनाची लांबी त्यांच्या लांबीच्या गुणाकाराच्या समान असते जर ते लंब असतील आणि जर सदिश समांतर किंवा समांतर असतील तर ते शून्यावर कमी होते.

सदिश उत्पादनाची व्याख्या वेगवेगळ्या प्रकारे आणि सैद्धांतिकदृष्ट्या कोणत्याही परिमाणाच्या जागेत करता येते. nआपण उत्पादनाची गणना करू शकता n-1वेक्टर, त्या सर्वांसाठी लंबवत एकच वेक्टर मिळवणे. परंतु जर उत्पादन सदिश परिणामांसह गैर-क्षुल्लक बायनरी उत्पादनांपुरते मर्यादित असेल, तर पारंपारिक वेक्टर उत्पादन केवळ तीन आयामांमध्ये परिभाषित केले जाते आणि सात-आयामीमोकळी जागा परिणाम वेक्टर उत्पादन, स्केलर प्रमाणे, यावर अवलंबून असते मेट्रिक्सयुक्लिडियन जागा.

वेक्टर कोऑर्डिनेट्समधून गणना करण्याच्या सूत्राच्या विपरीत डॉट उत्पादनतीन आयामांमध्ये आयताकृती समन्वय प्रणाली, क्रॉस उत्पादनासाठी सूत्र अवलंबून असते अभिमुखताआयताकृती समन्वय प्रणाली किंवा, दुसऱ्या शब्दांत, त्याचे " चिरालिटी».

वेक्टरचे मिश्रित उत्पादन

मिश्रित उत्पादन वेक्टर - स्केलर उत्पादन वेक्टरवर वेक्टर उत्पादन वेक्टरआणि:

कधी कधी म्हणतात ट्रिपल स्केलर उत्पादन vectors, वरवर पाहता परिणाम आहे की वस्तुस्थितीमुळे स्केलर(अधिक तंतोतंत - स्यूडोस्केलर).

भौमितिक अर्थ:मिश्रित उत्पादनाचे मॉड्यूलस संख्यात्मकदृष्ट्या व्हॉल्यूमच्या समान असते समांतर पाईप केलेले, सुशिक्षित वेक्टर .

मिश्रित तुकडा स्क्यू-सममितीयत्याच्या सर्व युक्तिवादांच्या संबंधात:

म्हणजेच, कोणत्याही दोन घटकांची पुनर्रचना केल्याने उत्पादनाचे चिन्ह बदलते. ते त्याचे पालन करते

विशेषतः,

वापरून मिश्रित काम सोयीस्करपणे लिहिता येते लेव्ही-सिविटा चिन्ह (टेन्सर):

(ऑर्थोनॉर्मल आधारावर शेवटच्या सूत्रामध्ये, सर्व निर्देशांक कमी म्हणून लिहिले जाऊ शकतात; या प्रकरणात, हे सूत्र थेट निर्धारकासह सूत्राची पुनरावृत्ती करते, तथापि, या प्रकरणात एक गुणक (-1) स्वयंचलितपणे प्राप्त होतो डावे तळ).

विमानात कार्टेशियन आयताकृती समन्वय प्रणाली.

चला विमानावर दोन परस्पर लंब सरळ रेषा घेऊ - दोन समन्वय अक्ष Ox आणि Oy वर दर्शविलेल्या सकारात्मक दिशानिर्देशांसह (चित्र 1). Ox आणि Oy या सरळ रेषांना समन्वय अक्ष म्हणतात, त्यांच्या छेदनबिंदूचा बिंदू O हा निर्देशांकांचा उगम आहे.

निवडलेल्या स्केल युनिटसह Ox, Oy या समन्वय अक्षांना विमानावरील कार्टेशियन आयताकृती (किंवा आयताकृती) समन्वय प्रणाली म्हणतात.

प्लेनच्या एका अनियंत्रित बिंदू M ला दोन संख्या देऊ: abscissa x, बिंदू M पासून Oy अक्षापर्यंतच्या अंतराच्या समान, M Oy च्या उजवीकडे असल्यास "+" चिन्हासह घेतले जाते आणि M Oy च्या डावीकडे असल्यास “-” चिन्ह; y ordinate, बिंदू M पासून Ox अक्षापर्यंतच्या अंतराच्या समान, M Ox च्या वर असल्यास "+" चिन्हासह आणि M Ox च्या खाली असल्यास "-" चिन्हासह. abscissa x आणि ordinate y यांना M(x;y) बिंदूचे कार्टेशियन आयताकृती निर्देशांक म्हणतात.

मूळमध्ये निर्देशांक आहेत (0;0). समन्वय अक्ष विमानाला चार भागांमध्ये विभागतात ज्याला चतुर्थांश किंवा चतुर्थांश म्हणतात (कधीकधी समन्वय कोन देखील म्हणतात). धनात्मक अर्ध-अक्ष Ox आणि Oy मधील समतल भागाला प्रथम चतुर्थांश म्हणतात. पुढे, चतुर्भुज घड्याळाच्या उलट दिशेने क्रमांकित केले जातात (चित्र 2). पहिल्या क्वाड्रंटच्या सर्व बिंदूंसाठी x>0, y>0; क्वाड्रंट x च्या बिंदू I साठी<0, у>0, I I I चतुर्थांश x मध्ये<0, у<0 и в IV квадранте х>0, y<0.

ध्रुवीय समन्वय.

ध्रुवीय समन्वय प्रणाली- द्विमितीय समन्वय प्रणाली ज्यामध्ये विमानावरील प्रत्येक बिंदू दोन संख्यांनी परिभाषित केला जातो - ध्रुवीय कोन आणि ध्रुवीय त्रिज्या. ध्रुवीय समन्वय प्रणाली विशेषतः अशा प्रकरणांमध्ये उपयुक्त आहे जिथे बिंदूंमधील संबंध त्रिज्या आणि कोनांच्या संदर्भात अधिक सहजपणे दर्शवले जातात; अधिक सामान्य मध्ये कार्टेशियनकिंवा आयताकृती समन्वय प्रणाली, असे संबंध केवळ अर्ज करून स्थापित केले जाऊ शकतात त्रिकोणमितीयसमीकरणे

ध्रुवीय समन्वय प्रणाली एका किरणाद्वारे परिभाषित केली जाते, ज्याला शून्य किंवा ध्रुवीय अक्ष म्हणतात. ज्या बिंदूतून हा किरण निघतो त्याला उगम किंवा ध्रुव म्हणतात. विमानावरील कोणताही बिंदू दोन ध्रुवीय निर्देशांकांद्वारे परिभाषित केला जातो: रेडियल आणि कोणीय. रेडियल समन्वय (सामान्यतः द्वारे दर्शविला जातो) एका बिंदूपासून उत्पत्तीपर्यंतच्या अंतराशी संबंधित असतो. कोनीय समन्वय, याला ध्रुवीय कोन किंवा सुद्धा म्हणतात दिगंशआणि दर्शविले जाते , या बिंदूवर जाण्यासाठी ध्रुवीय अक्ष घड्याळाच्या उलट दिशेने फिरवला पाहिजे त्या कोनाइतका आहे.

अशा प्रकारे परिभाषित केलेल्या रेडियल समन्वयातून मूल्ये घेऊ शकतात शून्यआधी अनंत, आणि कोनीय समन्वय 0° ते 360° पर्यंत बदलतो. तथापि, सोयीसाठी, ध्रुवीय समन्वयाच्या मूल्यांची श्रेणी पलीकडे वाढविली जाऊ शकते

विमानावरील सरळ रेषेचे समीकरण

Ax + Wu + C = 0,

शिवाय, स्थिरांक A आणि B एकाच वेळी शून्याच्या समान नाहीत. या पहिल्या क्रमाचे समीकरण म्हणतात सरळ रेषेचे सामान्य समीकरण. A, B आणि C स्थिरांकांच्या मूल्यांवर अवलंबून, खालील विशेष प्रकरणे शक्य आहेत:

C = 0, A ≠0, B ≠ 0 - सरळ रेषा उगमस्थानातून जाते

A = 0, B ≠0, C ≠0 (बाय + C = 0) - ऑक्स अक्षाच्या समांतर सरळ रेषा

B = 0, A ≠0, C ≠ 0 (Ax + C = 0) – Oy अक्षाच्या समांतर सरळ रेषा

B = C = 0, A ≠0 - सरळ रेषा Oy अक्षाशी एकरूप आहे

A = C = 0, B ≠0 - सरळ रेषा ऑक्स अक्षाशी जुळते

कोणत्याही प्रारंभिक परिस्थितीनुसार सरळ रेषेचे समीकरण वेगवेगळ्या स्वरूपात सादर केले जाऊ शकते.

रेषेचे समीकरण वापरण्याची मुख्य कार्ये

उत्तर देऊ शकत नाही

द्वितीय क्रम वक्र

द्वितीय क्रम वक्र- बिंदूंचे भौमितिक स्थान ज्यांचे कार्टेशियन आयताकृती समन्वय फॉर्मचे समीकरण पूर्ण करतात

ज्यामध्ये किमान एक गुणांक शून्यापेक्षा वेगळा आहे.

संख्या क्रम आणि कार्य मर्यादा

संख्या क्रम मर्यादा. एक संख्या क्रम विचारात घ्या ज्याची सामान्य संज्ञा काही संख्येपर्यंत पोहोचते a अनुक्रमांक वाढवत आहे n. या प्रकरणात, संख्या क्रम असल्याचे म्हटले जाते मर्यादा. या संकल्पनेची अधिक कठोर व्याख्या आहे.

या व्याख्येचा अर्थ असा आहे aतेथे आहे मर्यादासंख्या क्रम जर त्याची सामान्य संज्ञा मर्यादेशिवाय जवळ येत असेल aवाढीसह n. भौमितिकदृष्ट्या, याचा अर्थ असा आहे की कोणत्याही > 0 साठी अशी संख्या सापडू शकते एनपासून सुरू होते n > एन सर्वअनुक्रमाचे सदस्य मध्यांतराच्या आत स्थित आहेत ( a a). मर्यादा असलेला क्रम म्हणतात अभिसरण; अन्यथा - भिन्न.

क्रम म्हणतात मर्यादित, अशी संख्या अस्तित्वात असल्यास एमकाय | u n | एम  सगळ्यांसाठी n . वाढत्या किंवा कमी होणाऱ्या क्रमाला म्हणतात नीरस.

मर्यादा आणि त्यांच्या अनुप्रयोगांबद्दल मूलभूत प्रमेये

प्रमेय १ . (समानतेच्या मर्यादेपर्यंत जाण्याबद्दल)जर दोन फंक्शन्स एका विशिष्ट बिंदूच्या आसपास समान मूल्ये घेतात, तर या बिंदूवर त्यांची मर्यादा एकसारखी असते.

प्रमेय 2. (असमानतेच्या मर्यादेपर्यंत जाण्याबद्दल)फंक्शनचे मूल्य असल्यास f(x) एका विशिष्ट बिंदूच्या शेजारच्या भागात फंक्शनच्या संबंधित मूल्यांपेक्षा जास्त नसावे g(x) , नंतर फंक्शनची मर्यादा f(x) या टप्प्यावर फंक्शनची मर्यादा ओलांडत नाही g(x) .

प्रमेय 3 . स्थिरांकाची मर्यादा ही स्थिरांकाच्या बरोबरीची असते.

पुरावा. f(x)=cचला ते सिद्ध करूया.

चला एक अनियंत्रित >0 घेऊ.  तुम्ही कोणतेही घेऊ शकता

सकारात्मक संख्या. नंतर येथे

प्रमेय 4. कार्यमध्ये दोन भिन्न मर्यादा असू शकत नाहीत

एक बिंदू.

पुरावा. याच्या उलट गृहीत धरू. द्या

आणि .

द्वारे मर्यादा आणि अनंत कार्य यांच्यातील कनेक्शनवरील प्रमेय:

f(x)- ए= - b.m येथे,

f(x)- बी= - b.m येथे

या समानता वजा केल्यास, आम्हाला मिळते:

बी-ए= - .

येथे समानतेच्या दोन्ही बाजूंच्या मर्यादेपर्यंत, आमच्याकडे आहे:

बी-ए=0, म्हणजे बी=ए. आम्हाला एक विरोधाभास मिळतो जो प्रमेय सिद्ध करतो.

प्रमेय 5. फंक्शन्सच्या बीजगणितीय बेरीजच्या प्रत्येक पदाला मर्यादा असल्यास, बीजगणितीय बेरीजची देखील मर्यादा असते आणि बीजगणितीय बेरजेची मर्यादा मर्यादेच्या बीजगणितीय बेरजेइतकी असते.

.

पुरावा. द्या , , .

नंतर, द्वारे मर्यादा आणि b मधील कनेक्शनवरील प्रमेय.मी. कार्ये:

कुठे - b.m येथे

या समानता बीजगणितानुसार जोडूया:

f(x)+ g(x)- h(x-(A+B-C)= ,

कुठे b.m येथे

मर्यादा आणि b.m यांच्यातील कनेक्शनबद्दलच्या प्रमेयानुसार. वैशिष्ट्ये:

A+B-C= .

प्रमेय 6. फंक्शन्सच्या मर्यादित संख्येच्या उत्पादनाच्या प्रत्येक घटकाला मर्यादा असल्यास, उत्पादनाची देखील मर्यादा आहे आणि उत्पादनाची मर्यादा मर्यादेच्या गुणाकाराच्या समान आहे.

.

परिणाम.स्थिर घटक मर्यादा चिन्हाच्या पलीकडे जाऊ शकतो.

.

प्रमेय 7. जर कार्ये f(x) आणि g(x) मर्यादा आहे,

आणि , नंतर त्यांच्या भागाला देखील मर्यादा आहे, आणि भागाची मर्यादा मर्यादेच्या भागाकाराच्या समान आहे.

, .

कार्याची सातत्य

अंजीर मध्ये. 15, आणि फंक्शनचा आलेख दर्शविला आहे . त्याला सतत आलेख म्हणणे स्वाभाविक आहे कारण तो कागदावरून न उचलता पेन्सिलच्या एका हालचालीने काढता येतो. चला एक अनियंत्रित बिंदू (संख्या) सेट करूया. त्याच्या जवळचा आणखी एक बिंदू फॉर्ममध्ये लिहिला जाऊ शकतो, जेथे एक सकारात्मक किंवा ऋण संख्या आहे ज्याला वाढ म्हणतात. फरक

वाढीशी संबंधित बिंदूवर फंक्शनची वाढ म्हणतात. इथे अभिप्रेत आहे ते . अंजीर मध्ये. 15, आणि विभागाच्या लांबीच्या समान आहे.

आम्ही शून्याकडे प्रयत्न करू; मग प्रश्नातील फंक्शनसाठी, हे स्पष्टपणे शून्याकडे कल असेल:

. (1)

आता चित्र 15, b मधील आलेखाचा विचार करू. यात दोन सतत तुकडे असतात आणि. तथापि, हे तुकडे सतत जोडलेले नसतात, आणि म्हणूनच आलेखाला खंडित म्हणणे स्वाभाविक आहे. आलेखाने बिंदूवर एकल-मूल्य असलेले कार्य चित्रित करण्यासाठी, आपण हे मान्य करूया की ते जोडणाऱ्या खंडाच्या लांबीच्या समान आहे आणि ; याचे चिन्ह म्हणून, बिंदू ग्राफवर वर्तुळासह चित्रित केला आहे, तर बिंदूवर एक बाण काढलेला आहे, जो आलेखाशी संबंधित नाही हे दर्शवितो. जर बिंदू आलेखाशी संबंधित असेल, तर बिंदूवर फंक्शनचे दोन मूल्य असेल.

आता आपण एक वाढ जोडू आणि फंक्शनची संबंधित वाढ निश्चित करू:

जर आपला कल शून्याकडे असेल, तर आता शून्याकडे कशाचा कल असेल हे आता सांगता येणार नाही. शून्याकडे झुकणाऱ्या नकारात्मक लोकांसाठी हे खरे आहे, परंतु सकारात्मक लोकांसाठी हे अजिबात खरे नाही: आकृती दर्शवते की, जर सकारात्मक राहिल्यास, शून्याकडे झुकत असेल, तर संबंधित वाढ ही लांबीच्या समान सकारात्मक संख्येकडे झुकते. विभाग

या विचारांनंतर, या विभागातील एका बिंदूवर सतत मध्यांतरावर परिभाषित केलेल्या फंक्शनला कॉल करणे स्वाभाविक आहे जर या बिंदूवर त्याची वाढ, वाढीशी संबंधित, कोणत्याही प्रकारे शून्याकडे झुकत असेल. हे (सातत्यतेचे गुणधर्म) संबंधाच्या स्वरूपात लिहिलेले आहे (1) किंवा याप्रमाणे:

एंट्री (2) असे वाचते: कोणत्याही कायद्यानुसार जेव्हा ती शून्याकडे झुकते तेव्हा मर्यादा शून्याच्या बरोबरीची असते. तथापि, "कोणत्याही कायद्यानुसार" ही अभिव्यक्ती सहसा वगळली जाते, ती सूचित करते.

जर बिंदूवर परिभाषित केलेले कार्य निरंतर नसेल, म्हणजे, जर गुणधर्म (2) शून्याकडे झुकण्याच्या किमान एका मार्गाने धारण करत नसेल, तर त्यास बिंदूवर खंडित असे म्हणतात.

अंजीर मध्ये दर्शविलेले कार्य. 15, a, कोणत्याही बिंदूवर सतत असते, परंतु अंजीर मध्ये दर्शविलेले कार्य. 15, b, स्पष्टपणे, कोणत्याही बिंदूवर, बिंदूचा अपवाद वगळता सतत असतो, कारण नंतरच्यासाठी, संबंध (2) जेव्हा सकारात्मक राहतो तेव्हा समाधानी नसते.

खंडावरील (मध्यांतर) कोणत्याही बिंदूवर सतत असणाऱ्या कार्याला त्या खंडावर (मध्यांतर) सतत म्हणतात.

एक सतत फंक्शन गणितीयदृष्ट्या एक गुणधर्म व्यक्त करते ज्याचा आपण व्यवहारात अनेकदा सामना करतो, म्हणजे स्वतंत्र व्हेरिएबलमधील एक लहान वाढ अवलंबून व्हेरिएबल (फंक्शन) मधील लहान वाढीशी संबंधित असते. अखंड कार्याची उत्कृष्ट उदाहरणे म्हणजे शरीराच्या गतीचे विविध नियम, शरीराने वेळेवर प्रवास केलेल्या मार्गाचे अवलंबित्व व्यक्त करतात. वेळ आणि जागा सतत चालू असतात. हा किंवा तो गतीचा नियम त्यांच्या दरम्यान एक विशिष्ट सतत कनेक्शन स्थापित करतो, ज्याची वैशिष्ट्य म्हणजे वेळेची एक लहान वाढ पथाच्या लहान वाढीशी संबंधित आहे.

मनुष्य त्याच्या सभोवतालच्या तथाकथित सतत माध्यमांचे निरीक्षण करून निरंतरतेच्या अमूर्ततेकडे आला - घन, द्रव किंवा वायू, उदाहरणार्थ धातू, पाणी, हवा. खरं तर, कोणतेही भौतिक माध्यम म्हणजे एकमेकांपासून विभक्त झालेल्या मोठ्या संख्येने हलणारे कण. तथापि, हे कण आणि त्यांच्यातील अंतर हे माध्यमांच्या आकारमानाच्या तुलनेत इतके लहान आहेत की एखाद्याला मॅक्रोस्कोपिक भौतिक घटनांमध्ये सामोरे जावे लागते की अशा अनेक घटनांचा अभ्यास केला जात असलेल्या माध्यमाच्या वस्तुमानाचा अंदाजे विचार केला तर त्यांचा चांगला अभ्यास केला जाऊ शकतो. त्याने व्यापलेल्या जागेत कोणतेही अंतर न ठेवता सतत वितरित केले जाते. अनेक भौतिक शाखा या गृहीतकावर आधारित आहेत, उदाहरणार्थ हायड्रोडायनॅमिक्स, एरोडायनॅमिक्स आणि लवचिकता सिद्धांत. इतर अनेक विषयांप्रमाणेच सातत्य ही गणितीय संकल्पना नैसर्गिकरित्या या विषयांमध्ये मोठी भूमिका बजावते.

सतत फंक्शन्स फंक्शन्सचा मुख्य वर्ग बनवतात ज्यासह गणितीय विश्लेषण चालते.

सतत फंक्शन्सची उदाहरणे प्राथमिक फंक्शन्स आहेत (खाली § 3.8 पहा). ते ज्या ठिकाणी परिभाषित केले आहेत त्या बदलाच्या अंतराने ते सतत असतात.

गणितातील अखंड कार्ये निसर्गात आढळणाऱ्या अखंड प्रक्रिया प्रतिबिंबित करतात. प्रभावादरम्यान, उदाहरणार्थ, शरीराची गती अचानक बदलते. अनेक गुणवत्तेची संक्रमणे जंपसह असतात. उदाहरणार्थ, एक ग्रॅम पाण्याचे तापमान (बर्फ) आणि त्यात असलेल्या उष्णतेच्या कॅलरीजचे प्रमाण, जेव्हा ते आणि दरम्यान बदलते, जर आपण पारंपारिकपणे असे गृहीत धरले की , च्या मूल्यावर, खालील सूत्रांद्वारे व्यक्त केले जाते:

आम्ही गृहीत धरतो की बर्फाची उष्णता क्षमता 0.5 आहे. जेव्हा हे कार्य अनिश्चित होते - बहु-मूल्यवान; सोयीसाठी, आम्ही हे मान्य करू शकतो की यासाठी खूप निश्चित मूल्य लागते, उदाहरणार्थ. फंक्शन, येथे स्पष्टपणे खंडित आहे, अंजीर मध्ये दर्शविले आहे. 16.

एका बिंदूवर फंक्शनची सातत्य परिभाषित करू.

फंक्शनला एका बिंदूवर सतत म्हटले जाते, जर ते या बिंदूच्या काही परिसरात परिभाषित केले असेल, बिंदूसह, आणि जर या बिंदूवर त्याची वाढ, युक्तिवादाच्या वाढीशी संबंधित, शून्य असेल:

जर आपण ठेवले तर, आपल्याला येथे सातत्य ची खालील समतुल्य व्याख्या मिळते: फंक्शन एका बिंदूवर सतत असते जर ते या बिंदूच्या काही शेजारी परिभाषित केले असेल, बिंदूसह, आणि जर

; (4)

किंवा भाषेत देखील: जर प्रत्येकासाठी असे असेल तर

समानता (4) खालीलप्रमाणे देखील लिहिली जाऊ शकते:

. (4’)

हे दर्शविते की सतत कार्याच्या चिन्हाखाली एखादी व्यक्ती मर्यादेपर्यंत जाऊ शकते.

उदाहरण 1. स्थिरांक हे असे कार्य आहे जे कोणत्याही बिंदूवर सतत असते. खरं तर, बिंदू फंक्शनच्या मूल्याशी संबंधित आहे, बिंदू त्याच मूल्याशी संबंधित आहे . म्हणून

.

उदाहरण 2. फंक्शन कोणत्याही मूल्यासाठी सतत असते कारण आणि म्हणून, साठी.

उदाहरण 3. फंक्शन कोणत्याहीसाठी सतत असते. खरंच,

पण प्रत्येकासाठी असमानता आहे

जर , तर हे अंजीर पासून खालीलप्रमाणे आहे. 17, जे त्रिज्या 1 चे वर्तुळ दर्शविते (लांबीचा चाप तिच्याद्वारे जोडलेल्या जीवापेक्षा मोठा आहे, ज्याची लांबी आहे). जेव्हा असमानता (6) समानतेमध्ये बदलते. जर तर . शेवटी, जर, तर . (5) पासून (6) वर आधारित ते खालीलप्रमाणे आहे

,

पण मग साहजिकच

आम्ही असेही म्हणू शकतो की प्रत्येकासाठी असे शोधणे शक्य आहे

एक महत्त्वाचे प्रमेय लक्षात घेऊ या.

प्रमेय 1. जर फंक्शन्स आणि एका बिंदूवर सतत असतील, तर त्यांची बेरीज, फरक, गुणाकार आणि भागफल (at) देखील या बिंदूवर सतत असतात.

हे प्रमेय थेट प्रमेय 6 §3.2 चे अनुसरण करते, या प्रकरणात ते लक्षात घेऊन

फंक्शन (कॉम्प्लेक्स फंक्शन) पासून फंक्शनच्या सातत्य बद्दल एक महत्वाची प्रमेय देखील सत्य आहे.

प्रमेय 2. बिंदूवर सतत असणारे फंक्शन आणि बिंदूवर सतत असणारे दुसरे फंक्शन देऊ. मग जटिल कार्य बिंदूवर सतत आहे.

पुरावा. लक्षात घ्या की एखाद्या बिंदूवर फंक्शनच्या सातत्यच्या व्याख्येनुसार ते या बिंदूच्या काही शेजारच्या भागात परिभाषित केले गेले आहे. म्हणून

येथे एक प्रतिस्थापन सादर केले आहे आणि बिंदूवरील सातत्य लक्षात घेतले आहे .

उदाहरण 4. कार्य

जेथे स्थिर गुणांक असतात, त्याला पदवीचे बहुपद म्हणतात. हे कोणासाठीही निरंतर आहे. शेवटी, प्राप्त करण्यासाठी, स्थिर संख्या आणि कार्यावर आधारित, मर्यादित संख्येच्या अंकगणित ऑपरेशन्स करणे आवश्यक आहे - बेरीज, वजाबाकी आणि गुणाकार. परंतु स्थिरांक हे एक सतत कार्य आहे (उदाहरण 1 पहा), आणि एक कार्य देखील सतत असते (उदाहरण 2 पहा), त्यामुळे प्रमेय 1 वरून सातत्य येते.

उदाहरण 5. फंक्शन सतत आहे. ही दोन सतत कार्यांची रचना आहे: , .

उदाहरण 6. कार्य

विनिर्दिष्ट साठी सतत आहे , कारण (प्रमेय 1 पहा) ते अखंड फंक्शन्सच्या भागाकाराच्या भागाच्या बरोबरीचे आहे आणि विभाजक शून्य (निर्दिष्ट केलेल्या साठी) च्या समान नाही.

उदाहरण 7. कार्य

कोणत्याहीसाठी सतत असते, कारण ती सतत फंक्शन्सची रचना आहे: , , (प्रमेय 2 पहा).

उदाहरण 8. फंक्शन सतत आहे कारण

उदाहरण 9. जर एखाद्या बिंदूवर फंक्शन सतत असेल, तर फंक्शन देखील या बिंदूवर सतत असेल.

हे प्रमेय 2 आणि उदाहरण 8 वरून पुढे आले आहे, कारण फंक्शन ही दोन सतत फंक्शन्सची रचना आहे, .

फंक्शनच्या मर्यादेसाठी §3.2 च्या संबंधित प्रमेय 1 आणि 2 चे थेट पालन करणारे आणखी दोन प्रमेय लक्षात घेऊ.

प्रमेय 3. जर एखाद्या बिंदूवर फंक्शन सतत असेल, तर या बिंदूचा एक अतिपरिचित क्षेत्र आहे ज्यावर तो बद्ध आहे.

प्रमेय 4. जर फंक्शन बिंदूवर सतत असेल आणि , तर त्या बिंदूचा शेजार आहे

.

शिवाय, जर, तर

आणि जर, तर

व्युत्पन्न संकल्पना.

व्युत्पन्न(एका ​​बिंदूवर कार्ये) - मूलभूत संकल्पना विभेदक कॅल्क्युलस, फंक्शनच्या बदलाचा दर दर्शवितो (दिलेल्या बिंदूवर). म्हणून परिभाषित केले आहे मर्यादाफंक्शनची वाढ आणि त्याची वाढ यांच्यातील संबंध युक्तिवादजेव्हा युक्तिवाद वाढतो शून्य, अशी मर्यादा अस्तित्वात असल्यास. ज्या फंक्शनमध्ये मर्यादित व्युत्पन्न (काही टप्प्यावर) असते त्याला भिन्नता (त्या टप्प्यावर) म्हणतात.

व्युत्पन्न गणना करण्याच्या प्रक्रियेस म्हणतात भिन्नता. उलट प्रक्रिया - शोधणे अँटीडेरिव्हेटिव्ह - एकत्रीकरण.

डेरिव्हेटिव्ह्जचा भौमितीय आणि यांत्रिक अर्थ..

भिन्नतेचे नियम.

फंक्शन्सच्या बीजगणितीय बेरीजचे व्युत्पन्न

प्रमेय १. व्युत्पन्नदोन भिन्न कार्यांची बेरीज (फरक) ही या फंक्शन्सच्या डेरिव्हेटिव्हच्या बेरजेशी (फरक) समान आहे:

(u±v)" = u"±v"

परिणाम. भिन्न कार्यांच्या मर्यादित बीजगणितीय बेरीजचे व्युत्पन्न हे पदांच्या व्युत्पन्नांच्या समान बीजगणितीय बेरजेइतके असते. उदाहरणार्थ,

(u - v + w)" = u" - v" + w"

फंक्शन्सच्या उत्पादनाचे व्युत्पन्न द्वारे निर्धारित केले जाते

प्रमेय 2. दोन भिन्न कार्यांच्या गुणाकाराचे व्युत्पन्न पहिल्या फंक्शनच्या गुणाकाराच्या आणि दुसऱ्याचे व्युत्पन्न अधिक दुसऱ्या फंक्शनचे उत्पादन आणि पहिल्याचे व्युत्पन्न समान असते, म्हणजे.

(uv)" = u"v + uv"

परिणाम 1. व्युत्पन्न (cv)" = cv" (c = const) च्या चिन्हातून स्थिर घटक काढला जाऊ शकतो.

परिणाम 2. अनेक भिन्न कार्यांच्या उत्पादनाचे व्युत्पन्न इतर सर्वांनी केलेल्या प्रत्येकाच्या व्युत्पन्नाच्या उत्पादनांच्या बेरजेइतके असते.

उदाहरणार्थ, (uvw)" = u"vw + uv"w + uvw"

दोन फंक्शन्सच्या भागाचे व्युत्पन्न

खालील प्रमेयाद्वारे व्यक्त केले जाते.

प्रमेय 3. दोन भिन्न कार्यांच्या भागाचे व्युत्पन्न सूत्राद्वारे निर्धारित केले जाते

जटिल कार्याचे व्युत्पन्न द्वारे व्यक्त केले जाते

प्रमेय 4. जर y = f(u) आणि u = (ф(x)) त्यांच्या वितर्कांची भिन्न कार्ये आहेत, तर जटिल कार्याचे व्युत्पन्न y = f (ф(x)) अस्तित्त्वात आहे आणि इंटरमीडिएट आर्ग्युमेंटच्या संदर्भात या फंक्शनच्या डेरिव्हेटिव्हच्या गुणाकाराच्या आणि स्वतंत्र व्हेरिएबलच्या संदर्भात इंटरमीडिएट वितर्काच्या व्युत्पन्नाच्या समान आहे, म्हणजे.

मध्ये खूप वेळा डेरिव्हेटिव्ह्जवरील गणितातील चाचण्याजटिल कार्ये दिली आहेत, उदाहरणार्थ, y = sin(cos5x). अशा फंक्शनचे व्युत्पन्न -5sin5x*sin(cos5x) च्या बरोबरीचे असते.

खालील व्हिडिओमध्ये जटिल कार्याची गणना करण्याचे उदाहरण पहा

प्राथमिक कार्यांचे व्युत्पन्न.

भिन्नता समस्या सोडवताना, एखाद्याला फंक्शन्सचे व्युत्पन्न शोधणे आवश्यक आहे विविध वर्ग. या लेखात आपण मुख्य पाहू भिन्नता नियम, जे डेरिव्हेटिव्ह शोधताना आम्ही सतत वापरतो. आम्ही हे सर्व नियम फंक्शनच्या डेरिव्हेटिव्हच्या व्याख्येवर आधारित सिद्ध करू आणि निश्चितपणे यावर लक्ष केंद्रित करू तपशीलवार उपायत्यांच्या अर्जाचे तत्त्व समजून घेण्यासाठी उदाहरणे.

भिन्नतेचे नियम सिद्ध करताना, आम्ही असे गृहीत धरू की फंक्शन्स f(x) आणि g(x) काही अंतराल X वर भिन्न आहेत.

म्हणजेच, कोणत्याहीसाठी हे खरे आहे की, संबंधित फंक्शन्सची वाढ कुठे आहे.

दुसर्या पोस्ट मध्ये.

फरक करण्याच्या मूलभूत नियमांमध्ये हे समाविष्ट आहे:

व्युत्पन्न चिन्हाच्या पलीकडे एक स्थिर घटक पार पाडणे.

चला सूत्र सिद्ध करूया. डेरिव्हेटिव्हच्या व्याख्येनुसार आमच्याकडे आहे:

एक अनियंत्रित घटक मर्यादेपर्यंत जाण्याच्या चिन्हाच्या पलीकडे नेला जाऊ शकतो (हे मर्यादेच्या गुणधर्मांवरून ओळखले जाते), म्हणून

हे भिन्नतेच्या पहिल्या नियमाचा पुरावा पूर्ण करते.

डेरिव्हेटिव्ह्जचे सारणी आणि डेरिव्हेटिव्ह्ज शोधण्याचे नियम वापरण्यासाठी बऱ्याचदा प्रथम भिन्न कार्याचे स्वरूप सोपे करणे आवश्यक आहे. खालील उदाहरणे स्पष्टपणे याची पुष्टी करतात.

उदाहरण.

फंक्शन डिफरेंशन करा .

उपाय.

लॉगरिदमिक फंक्शनच्या गुणधर्मांवर आधारित, तुम्ही नोटेशनवर जाऊ शकता. लॉगरिदमिक फंक्शनचे व्युत्पन्न लक्षात ठेवणे आणि स्थिर घटक जोडणे बाकी आहे:

उदाहरण.

उपाय.

मूळ फंक्शनचे रूपांतर करूया .

आम्ही व्युत्पन्न चिन्हाच्या बाहेर गुणक ठेवण्याचा नियम लागू करतो आणि सारणीमधून घातांकीय कार्याचे व्युत्पन्न घेतो:

बेरीजचे व्युत्पन्न, फरकाचे व्युत्पन्न.

भिन्नतेचा दुसरा नियम सिद्ध करण्यासाठी, आम्ही व्युत्पन्नाची व्याख्या आणि सतत कार्याच्या मर्यादेचा गुणधर्म वापरतो.

त्याच प्रकारे, हे सिद्ध केले जाऊ शकते की n फंक्शन्सच्या बेरीज (फरक) चे व्युत्पन्न n डेरिव्हेटिव्हच्या बेरीज (फरक) च्या बरोबरीचे आहे.

उदाहरण.

फंक्शनचे व्युत्पन्न शोधा .

उपाय.

मूळ फंक्शनचे स्वरूप सोपे करू.

आम्ही व्युत्पन्न बेरीज (फरक) नियम वापरतो:

मागील परिच्छेदात, आम्ही सिद्ध केले की स्थिर घटक व्युत्पन्न चिन्हातून काढला जाऊ शकतो, म्हणून

डेरिव्हेटिव्ह्जचे सारणी वापरणे बाकी आहे:

फंक्शन्सच्या उत्पादनाचे व्युत्पन्न.

दोन फंक्शन्सच्या गुणाकारात फरक करण्याचा नियम सिद्ध करूया.

फंक्शन्सच्या गुणाकाराच्या वाढीच्या गुणोत्तराची मर्यादा आणि वितर्क वाढूया. आम्ही ते विचारात घेऊ आणि (आर्ग्युमेंटची वाढ शून्याकडे झुकत असल्याने फंक्शनची वाढ शून्य होते).

Q.E.D.

उदाहरण.

कार्य वेगळे करा .

उपाय.

IN या उदाहरणात. आम्ही उत्पादन व्युत्पन्न नियम लागू करतो:

आम्ही मूलभूत प्राथमिक कार्यांच्या डेरिव्हेटिव्ह्जच्या सारणीकडे वळतो आणि उत्तर मिळवतो:

उदाहरण.

फंक्शनचे व्युत्पन्न शोधा.

उपाय.

या उदाहरणात . त्यामुळे,

तीन फंक्शन्सच्या उत्पादनाचे व्युत्पन्न शोधण्याचे प्रकरण पाहू. तत्त्वतः, समान प्रणाली वापरून चार, पाच आणि पंचवीस कार्यांचे उत्पादन वेगळे करणे शक्य आहे.

उदाहरण.

फंक्शनचे वेगळेपण करा.

उपाय.

दोन फंक्शन्सच्या गुणाकाराच्या भिन्नतेच्या नियमापासून आपण पुढे जाऊ. फंक्शन f(x) म्हणून आम्ही उत्पादन (1+x)sinx चा विचार करू आणि g(x) म्हणून आम्ही lnx घेऊ:

शोधण्यासाठी आम्ही पुन्हा उत्पादन व्युत्पन्न नियम लागू करतो:

आम्ही व्युत्पन्न बेरीज नियम आणि व्युत्पन्न सारणी वापरतो:

चला निकाल बदलू:

तुम्ही बघू शकता, काहीवेळा तुम्हाला एका उदाहरणात अनेक भिन्नता नियम लागू करावे लागतात. यात काहीही क्लिष्ट नाही, मुख्य गोष्ट म्हणजे सातत्याने कार्य करणे आणि सर्वकाही एकत्र न करणे.

उदाहरण.

फंक्शनचे व्युत्पन्न शोधा.

उपाय.

फंक्शन अभिव्यक्तींमधील फरक दर्शवते आणि म्हणून

पहिल्या अभिव्यक्तीमध्ये आम्ही दोन व्युत्पन्नाचे चिन्ह म्हणून घेतो आणि दुसऱ्या अभिव्यक्तीमध्ये आम्ही उत्पादनामध्ये फरक करण्यासाठी नियम लागू करतो:

दोन कार्यांच्या भागाचे व्युत्पन्न (अपूर्णांकाचे व्युत्पन्न).

दोन फंक्शन्स (अपूर्णांक) च्या भागफलामध्ये फरक करण्याचा नियम सिद्ध करूया. . हे लक्षात घेण्यासारखे आहे की X मध्यांतरातील कोणत्याही x साठी g(x) नाहीसे होत नाही.

tion, ज्यामुळे समानता (3.10) ही सैद्धांतिक अभ्यास आणि अंदाजे गणनेमध्ये महत्त्वाची भूमिका बजावते.

फंक्शनचे व्युत्पन्न आणि भिन्नता शोधण्याच्या ऑपरेशनला म्हणतात भिन्नताहे कार्य. सामान्य नावदोन्ही ऑपरेशन्स त्यांच्या स्पष्ट अवलंबनाद्वारे स्पष्ट केल्या आहेत. फॉर्म्युला (3.8) च्या आधारे, फंक्शनचा फरक फक्त त्याच्या गुणाकाराने मिळवला जातो

वाहक त्रुटी ज्या फंक्शनच्या वाढीला त्याच्या भिन्नतेसह बदलताना उद्भवतात.

फंक्शनची वाढ आणि फरक शोधू

y = 3(x+ x) 2 + (x+ x) − 3 x2 − x= 6 x x+ 3(x) 2 + x= (6 x+ 1) x+ (x) 2 .

नंतर dy = (6 x + 1) x. चला x = 1 या बिंदूवर udy ची गणना करूया जर x = 0, 1 y = 7 0, 1 + 3 0, 01 = 0, 73; dy = 7 0 , 1 = 0 , 7 .

परिपूर्ण त्रुटी y − dy = 0.73 − 0.7 = 0.03 आहे, आणि संबंधित त्रुटी

y = 0 0 , , 03 73 ≈0 .04 .

3.5. बेरीज, गुणाकार आणि फंक्शन्सची व्युत्पन्न

आपण कोर्समधून प्रसिद्ध आठवूया हायस्कूलभिन्नता नियम, जे काही प्रकरणांमध्ये थेट परिभाषाचा अवलंब न करता फंक्शन्सचे डेरिव्हेटिव्ह शोधण्याची परवानगी देतात.

प्रमेय 3.3. जर फंक्शन्स u = u (x) आणि v = v (x)

वेगळे करण्यायोग्य

या समानता पदाचा dx ने गुणाकार केल्याने, आम्हाला भिन्नतेच्या दृष्टीने लिहिलेले समान नियम प्राप्त होतात

पुरावा. प्रमेयाच्या सर्व भागांचा पुरावा पूर्णपणे एकसमानपणे चालविला जात असल्याने, आम्ही त्यापैकी एक सिद्ध करू, उदाहरणार्थ, दुसरा.

y = uv दर्शवू. चला x increment x देऊ, आणि द्या

संदर्भित, आणि म्हणून सतत (प्रमेय 3.2), म्हणून

टेल व्युत्पन्न आणि विभेदक चिन्हांमधून काढले जाऊ शकते.

तीन घटकांच्या बाबतीत, क्रमाने सूत्र लागू करणे

(3.12), आम्हाला आढळते

(uvw) ′ = ((uv) w) ′ = (uv) ′ w+ (uv) w′+ (u′ v+ uv′ ) w+ uvw′ = = u ′ vw + uv ′ w + uvw ′.

कोणत्याही घटकांच्या उत्पादनामध्ये फरक करताना समान नियम वैध आहे.

पुढील परिच्छेदांमध्ये, मुख्य प्राथमिक कार्यांचे व्युत्पन्न प्राप्त केले जातील.

३.६. त्रिकोणमितीय कार्यांचे व्युत्पन्न

त्रिकोणमितीय फंक्शन्सचे डेरिव्हेटिव्ह शोधू या

चला पहिला मिळवूया. फंक्शन y ची वाढ = sin x at pointx, co-

दुसरे सूत्र अशाच प्रकारे सिद्ध झाले आहे. तिसरे आणि चौथे सूत्र प्राप्त होते जर स्पर्शिका आणि कोटँजेंट साइन आणि कोसाइनच्या संदर्भात व्यक्त केले गेले आणि सूत्र वापरला (3.13).

३.७. लॉगरिदमिक फंक्शन्समध्ये फरक करणे

चला त्यापैकी पहिले सिद्ध करूया. फंक्शन y ची वाढ = पॉइंटएक्सवर एक x लॉग करा, सह-

(आम्ही येथे आयडेंटिटी log a A = log a e ln A वापरला आहे).

३.८. जटिल कार्याचा भेद.

शक्ती आणि घातांकीय कार्यांचे व्युत्पन्न

y = f (u) या सूत्रांद्वारे क्लिष्ट फंक्शन y वितर्क देऊ द्या,

u = ϕ (x) (परिच्छेद १.४.३ पहा)

प्रमेय 3.4 (एक जटिल कार्याच्या व्युत्पन्न बद्दल). जर कार्ये

फंक्शन y ची वाढ y = f (u) . प्रमेयाच्या परिस्थितीनुसार फंक्शन y = f (u) हे विचाराधीन u या बिंदूवर वेगळे करण्यायोग्य असल्याने, या बिंदूवर त्याची वाढ फॉर्ममध्ये दर्शविली जाऊ शकते (व्याख्या 3.4 पहा)

x → 0, आम्ही (3.18) वर पोहोचतो.

समानता (3.18) पदाचा dx द्वारे संज्ञा गुणाकार केल्याने, आम्हाला जटिल कार्याच्या भिन्नतेसाठी एक अभिव्यक्ती मिळते

dy = f′ (u) du.

टिप्पणी. फंक्शन y = f (u) च्या भिन्नतेचे तंतोतंत समान स्वरूप असेल जर u ​​हा वितर्क फंक्शन नसून स्वतंत्र चल असेल. यालाच म्हणतात अपरिवर्तनीय मालमत्ता(स्वातंत्र्य) युक्तिवादाच्या संदर्भात भिन्नतेच्या स्वरूपाचे. हे लक्षात घेतले पाहिजे की जर u ​​स्वतंत्र व्हेरिएबल असेल तर du = u ही त्याची अनियंत्रित वाढ आहे, जर u ​​इंटरमीडिएट आर्ग्युमेंट असेल (म्हणजे फंक्शन), तर du हा या फंक्शनचा भिन्नता आहे, म्हणजे, a. मूल्य जे त्याच्या वाढीशी जुळत नाही u.

शेवटचे प्रमेय वापरून, भिन्नता सूत्रे मिळवणे सोपे आहे

शेवटच्या समानतेची डावी बाजू x चे जटिल कार्य आहे. शेवटच्या समानतेच्या दोन्ही बाजूंना x (जटिल फंक्शन म्हणून डावी बाजू) संदर्भात फरक करून, आम्ही प्राप्त करतो

1 y y′ =a 1 x ,

y ′ =ay x =ax x a =ax a − 1 .

हे दर्शविणे सोपे आहे की हा परिणाम x साठी देखील सत्य आहे< 0 , если только при

या प्रकरणात x α अर्थ प्राप्त होतो. पूर्वी, केस α = n साठी परिणाम प्राप्त झाला होता. दुसरे सूत्र असेच मिळते, ज्यावरून, a = e च्या विशेष प्रकरणात, शेवटचे सूत्र पुढे येते.

टिप्पणी. प्राथमिक लॉगरिथमचे तंत्र, जे पॉवर फंक्शन वेगळे करण्यासाठी सूत्र प्राप्त करण्यासाठी वापरले गेले होते, त्याला स्वतंत्र महत्त्व आहे आणि फंक्शनच्या लॉगरिथमच्या व्युत्पन्नाच्या नंतरच्या शोधाच्या संयोगाने म्हटले जाते.

lnx ) "= cosx lnx + sin x x .

त्यामुळे,

y ′ = x sin x (cosx lnx + sin x x)

टिप्पणी. गुंतागुंतीच्या फंक्शनमध्ये फरक करण्याचा नियम अस्पष्टपणे निर्दिष्ट केलेल्या फंक्शनचे व्युत्पन्न शोधण्यासाठी देखील लागू केला जाऊ शकतो.

खरंच, जर x आणि y मधला संबंध F (x, y) = 0 या स्वरूपात दिला असेल आणि हे समीकरण y च्या सापेक्ष सोडवता येण्याजोगे असेल, तर व्युत्पन्न y′ समीकरणातून शोधता येईल.

३.९. व्यस्त कार्याचा भेद.

व्यस्त त्रिकोणमितीय कार्यांचे भेद

दोन परस्पर दिले जाऊ द्या व्यस्त कार्ये y = f (x) आणि x = ϕ (y)

(खंड 1.4.8 पहा).

प्रमेय 3.5 (विलोम कार्याच्या व्युत्पन्न बद्दल). जर कार्ये