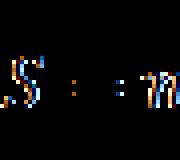Kā vienkāršot matemātisko izteiksmi. Video pamācība "Izteiksmju vienkāršošana

1. piezīme

Loģisko funkciju var uzrakstīt, izmantojot loģisku izteiksmi, un pēc tam varat doties uz loģisko ķēdi. Ir nepieciešams vienkāršot loģiskās izteiksmes, lai iegūtu pēc iespējas vienkāršāku (tātad lētāku) loģisko shēmu. Faktiski loģiskā funkcija, loģiskā izteiksme un loģiskā ķēde ir trīs dažādas valodas, kas runā par vienu un to pašu vienību.

Lai vienkāršotu loģiskās izteiksmes, izmantojiet loģikas algebras likumi.

Dažas transformācijas ir līdzīgas formulu pārveidojumiem klasiskajā algebrā (kopējā faktora iekavās, izmantojot komutācijas un kombinācijas likumus utt.), savukārt citas transformācijas ir balstītas uz īpašībām, kuru klasiskajām algebras operācijām nepiemīt (izmantojot sadales likumu konjunkcijai, likumi absorbcijas, līmēšanas, de Morgana likumi utt.).

Loģiskas algebras likumi ir formulēti loģisko pamatoperāciju veikšanai - “NOT” - inversija (nigācija), “UN” - konjunkcija (loģiskā reizināšana) un “OR” - disjunkcija (loģiskā saskaitīšana).

Dubultās noliegšanas likums nozīmē, ka darbība "NOT" ir atgriezeniska: ja to lietojat divas reizes, tad galu galā loģiskā vērtība nemainīsies.

Izslēgtā vidus likums nosaka, ka jebkura loģiskā izteiksme ir patiesa vai nepatiesa (“nav trešā”). Tāpēc, ja $A=1$, tad $\bar(A)=0$ (un otrādi), kas nozīmē, ka šo lielumu konjunkcija vienmēr ir vienāda ar nulli, bet disjunkcija ir vienāda ar vienu.

$((A + B) → C) \cdot (B → C \cdot D) \cdot C.$

Vienkāršosim šo formulu:

3. attēls

Tas nozīmē, ka $ A = 0 $, $ B = 1 $, $ C = 1 $, $ D = 1 $.

Atbilde: studenti $B$, $C$ un $D$ spēlē šahu, bet students $A$ nespēlē.

Vienkāršojot loģiskās izteiksmes, varat veikt šādu darbību secību:

1. Aizstāt visas “nepamata” darbības (ekvivalence, implikācija, XOR utt.) ar to izteiksmēm, izmantojot inversijas, konjunkcijas un disjunkcijas pamatoperācijas.
2. Paplašiniet sarežģītu izteiksmju inversijas saskaņā ar de Morgana noteikumiem tā, lai tikai atsevišķiem mainīgajiem būtu noliegšanas darbības.
3. Pēc tam vienkāršojiet izteiksmi, izmantojot iekavu izvēršanu, kopējo faktoru iekavās un citus loģikas algebras likumus.

2. piemērs

Šeit secīgi tiek lietots de Morgana likums, sadales likums, izslēgtā vidus likums, komutatīvais likums, atkārtošanās likums, atkal komutatīvais likums un absorbcijas likums.

Literatūra izteiksme (vai izteiksme ar mainīgajiem) ir matemātiskā izteiksme, kas sastāv no cipariem, burtiem un matemātisko darbību zīmēm. Piemēram, šī izteiksme ir burtiska:

a+b+4

Izmantojot burtiskas izteiksmes, varat pierakstīt likumus, formulas, vienādojumus un funkcijas. Spēja manipulēt ar burtiskām izteiksmēm ir labas algebras un augstākās matemātikas zināšanu atslēga.

Jebkura nopietna matemātikas problēma ir saistīta ar vienādojumu risināšanu. Un, lai varētu atrisināt vienādojumus, jums ir jāspēj strādāt ar burtiskām izteiksmēm.

Lai strādātu ar burtiskām izteiksmēm, labi jāapgūst pamata aritmētika: saskaitīšana, atņemšana, reizināšana, dalīšana, matemātikas pamatlikumi, daļskaitļi, darbības ar daļskaitļiem, proporcijas. Un ne tikai mācīties, bet kārtīgi izprast.

Mainīgie lielumi

Tiek saukti burti, kas ietverti burtiskās izteiksmēs mainīgie. Piemēram, izteiksmē a+b+4 burti ir mainīgie a Un b. Ja šo mainīgo vietā aizvietojam jebkurus skaitļus, tad burtiskā izteiksme a+b+4 pārvērtīsies par skaitlisko izteiksmi, kuras vērtību var atrast.

Tiek saukti skaitļi, kas ir aizstāti ar mainīgajiem mainīgās vērtības. Piemēram, mainīsim mainīgo vērtības a Un b. Izmantojiet vienādības zīmi, lai mainītu vērtības

a = 2, b = 3

Mēs esam mainījuši mainīgo vērtības a Un b. mainīgs a piešķirta vērtība 2 , mainīgs b piešķirta vērtība 3 . Rezultātā burtiskā izteiksme a+b+4 pārvērš parastā skaitliskā izteiksmē 2+3+4 kuras vērtību var atrast:

2 + 3 + 4 = 9

Ja mainīgie tiek reizināti, tie tiek rakstīti kopā. Piemēram, ieraksts ab nozīmē to pašu, ko ieraksts a × b. Ja mainīgo vietā aizstājam a Un b cipariem 2 Un 3 , tad mēs iegūstam 6

2 x 3 = 6

Kopā jūs varat arī ierakstīt skaitļa reizināšanu ar izteiksmi iekavās. Piemēram, tā vietā a × (b + c) var uzrakstīt a(b+c). Piemērojot reizināšanas sadales likumu, iegūstam a(b + c)=ab+ac.

Likmes

Burtiskajās izteiksmēs bieži var atrast apzīmējumu, kurā, piemēram, kopā ir rakstīts skaitlis un mainīgais 3a. Faktiski tas ir saīsinājums skaitļa 3 reizināšanai ar mainīgo. a un šis ieraksts izskatās 3×a .

Citiem vārdiem sakot, izteiksme 3a ir skaitļa 3 un mainīgā reizinājums a. Numurs 3 šajā darbā sauc koeficients. Šis koeficients parāda, cik reizes mainīgais tiks palielināts a. Šo izteiksmi var lasīt kā " a trīs vai trīs reizes A" vai "palieliniet mainīgā vērtību a trīs reizes", bet visbiežāk lasa kā "trīs a«

Piemēram, ja mainīgais a ir vienāds ar 5 , tad izteiksmes vērtība 3a būs vienāds ar 15.

3 x 5 = 15

runājot vienkārša valoda, koeficients ir skaitlis, kas ir pirms burta (pirms mainīgā).

Piemēram, var būt vairāki burti 5abc. Šeit koeficients ir skaitlis 5 . Šis koeficients parāda, ka mainīgo lielumu reizinājums abc palielinās piecas reizes. Šo izteiksmi var lasīt kā " abc piecas reizes" vai "palieliniet izteiksmes vērtību abc piecas reizes" vai "piecas abc«.

Ja mainīgo vietā abc aizvietojiet skaitļus 2, 3 un 4, pēc tam izteiksmes vērtību 5abc būs vienāds ar 120

5 x 2 x 3 x 4 = 120

Varat garīgi iedomāties, kā vispirms tika reizināti skaitļi 2, 3 un 4, un iegūtā vērtība palielinājās piecas reizes:

Koeficienta zīme attiecas tikai uz koeficientu un neattiecas uz mainīgajiem lielumiem.

Apsveriet izteiksmi −6b. Mīnuss koeficienta priekšā 6 , attiecas tikai uz koeficientu 6 , un neattiecas uz mainīgo b. Izpratne par šo faktu ļaus turpmāk nepieļaut kļūdas ar zīmēm.

Atrodiet izteiksmes vērtību −6b plkst b = 3.

−6b −6 × b. Skaidrības labad mēs uzrakstām izteiksmi −6b paplašinātā formā un aizstāt mainīgā vērtību b

−6b = −6 × b = −6 × 3 = −18

2. piemērs Atrodiet izteiksmes vērtību −6b plkst b = –5

Uzrakstīsim izteiksmi −6b paplašinātā formā

−6b = −6 × b = −6 × (−5) = 30

3. piemērs Atrodiet izteiksmes vērtību −5a+b plkst a = 3 Un b = 2

−5a+b ir saīsinātā forma vārdam −5 × a + b, tāpēc skaidrības labad mēs rakstām izteiksmi −5×a+b paplašinātā formā un aizstāt mainīgo vērtības a Un b

−5a + b = −5 × a + b = −5 × 3 + 2 = −15 + 2 = −13

Dažreiz burti tiek rakstīti bez koeficienta, piemēram a vai ab. Šajā gadījumā koeficients ir viens:

bet mērvienību tradicionāli nepieraksta, tāpēc viņi vienkārši raksta a vai ab

Ja pirms burta ir mīnuss, tad koeficients ir skaitlis −1 . Piemēram, izteiksme -a patiesībā izskatās −1a. Šis ir mīnus viens un mainīgā reizinājums a. Tas iznāca šādi:

−1 × a = −1a

Šeit slēpjas mazs triks. Izteicienā -a mīnus pirms mainīgā a faktiski attiecas uz "neredzamo vienību", nevis mainīgo a. Tāpēc, risinot problēmas, jums jābūt uzmanīgiem.

Piemēram, ņemot vērā izteiksmi -a un mums tiek lūgts atrast tā vērtību a = 2, tad skolā mainīgā vietā aizstājām divnieku a un saņemt atbildi −2 , īsti nekoncentrējoties uz to, kā tas izrādījās. Faktiski mīnus viens tika reizināts ar pozitīvu skaitli 2

-a = -1 × a

−1 × a = −1 × 2 = −2

Ja ir dota izteiksme -a un tam ir jāatrod tā vērtība a = –2, tad aizstājam −2 mainīgā vietā a

-a = -1 × a

–1 × a = –1 × (–2) = 2

Lai izvairītos no kļūdām, sākumā var skaidri uzrakstīt neredzamas vienības.

4. piemērs Atrodiet izteiksmes vērtību abc plkst a=2 , b=3 Un c=4

Izteiksme abc 1 × a × b × c. Skaidrības labad mēs uzrakstām izteiksmi abc a, b Un c

1 x a x b x c = 1 x 2 x 3 x 4 = 24

5. piemērs Atrodiet izteiksmes vērtību abc plkst a=−2 , b=−3 Un c=−4

Uzrakstīsim izteiksmi abc paplašinātā formā un aizstāt mainīgo vērtības a, b Un c

1 × a × b × c = 1 × (–2) × (–3) × (–4) = –24

6. piemērs Atrodiet izteiksmes vērtību − abc plkst a=3, b=5 un c=7

Izteiksme − abc ir saīsinātā forma vārdam −1 × a × b × c. Skaidrības labad mēs uzrakstām izteiksmi − abc paplašinātā formā un aizstāt mainīgo vērtības a, b Un c

−abc = −1 × a × b × c = –1 × 3 × 5 × 7 = –105

7. piemērs Atrodiet izteiksmes vērtību − abc plkst a=−2 , b=−4 un c=−3

Uzrakstīsim izteiksmi − abc paplašināts:

−abc = −1 × a × b × c

Aizstāt mainīgo vērtību a , b Un c

−abc = −1 × a × b × c = −1 × (−2) × (−4) × (−3) = 24

Kā noteikt koeficientu

Dažreiz ir jāatrisina problēma, kurā ir jānosaka izteiksmes koeficients. Principā šis uzdevums ir ļoti vienkāršs. Tas ir pietiekami, lai varētu pareizi reizināt skaitļus.

Lai noteiktu koeficientu izteiksmē, jums atsevišķi jāreizina šajā izteiksmē iekļautie skaitļi un atsevišķi jāreizina burti. Iegūtais skaitliskais koeficients būs koeficients.

1. piemērs 7 m × 5 a × (−3) × n

Izteiksme sastāv no vairākiem faktoriem. To var skaidri redzēt, ja izteiksme ir rakstīta izvērstā formā. Tas ir, darbojas 7 m Un 5a rakstīt formā 7 × m Un 5×a

7 × m × 5 × a × (–3) × n

Mēs piemērojam reizināšanas asociatīvo likumu, kas ļauj reizināt faktorus jebkurā secībā. Proti, atsevišķi reiziniet ciparus un atsevišķi reiziniet burtus (mainīgos):

−3 × 7 × 5 × m × a × n = –105 cilvēks

Koeficients ir −105 . Pēc pabeigšanas burtu daļu vēlams sakārtot alfabētiskā secībā:

-105 no rīta

2. piemērs Nosakiet koeficientu izteiksmē: −a×(−3)×2

−a × (−3) × 2 = −3 × 2 × (−a) = −6 × (−a) = 6a

Koeficients ir 6.

3. piemērs Nosakiet koeficientu izteiksmē:

Sareizināsim ciparus un burtus atsevišķi:

Koeficients ir –1. Lūdzu, ņemiet vērā, ka vienība netiek reģistrēta, jo koeficients 1 parasti netiek reģistrēts.

Šie šķietami vienkāršie uzdevumi ar mums var izspēlēt ļoti nežēlīgu joku. Bieži vien izrādās, ka koeficienta zīme ir iestatīta nepareizi: vai nu tiek izlaists mīnuss, vai, gluži pretēji, tas ir iestatīts veltīgi. Lai izvairītos no šīm kaitinošajām kļūdām, tas ir jāapgūst labā līmenī.

Termini burtiskā izteiksmē

Saskaitot vairākus skaitļus, tiek iegūta šo skaitļu summa. Skaitļus, kas summējas, sauc par terminiem. Var būt vairāki termini, piemēram:

1 + 2 + 3 + 4 + 5

Ja izteiksme sastāv no terminiem, to ir daudz vieglāk aprēķināt, jo to ir vieglāk pievienot nekā atņemt. Bet izteiksmē var būt ne tikai saskaitīšana, bet arī atņemšana, piemēram:

1 + 2 − 3 + 4 − 5

Šajā izteiksmē skaitļi 3 un 5 tiek atņemti, nevis pievienoti. Bet nekas neliedz mums aizstāt atņemšanu ar saskaitīšanu. Tad mēs atkal iegūstam izteiksmi, kas sastāv no terminiem:

1 + 2 + (−3) + 4 + (−5)

Tas nekas, ka cipari -3 un -5 tagad ir ar mīnusa zīmi. Galvenais ir tas, ka visi skaitļi šajā izteiksmē ir savienoti ar saskaitīšanas zīmi, tas ir, izteiksme ir summa.

Abi izteicieni 1 + 2 − 3 + 4 − 5 Un 1 + 2 + (−3) + 4 + (−5) ir vienādi ar vienu un to pašu vērtību - mīnus viens

1 + 2 − 3 + 4 − 5 = −1

1 + 2 + (−3) + 4 + (−5) = −1

Tādējādi izteiksmes vērtība necietīs no tā, ka mēs kaut kur aizstāsim atņemšanu ar saskaitīšanu.

Jūs varat arī aizstāt atņemšanu ar saskaitīšanu burtiskās izteiksmēs. Piemēram, apsveriet šādu izteiksmi:

7a + 6b - 3c + 2d - 4s

7a + 6b + (-3c) + 2d + (-4s)

Jebkurām mainīgo vērtībām a, b, c, d Un s izteiksmes 7a + 6b - 3c + 2d - 4s Un 7a + 6b + (-3c) + 2d + (-4s) būs vienāda ar to pašu vērtību.

Jums jābūt gatavam tam, ka skolotājs skolā vai skolotājs institūtā var nosaukt terminus pat tos skaitļus (vai mainīgos), kas tie nav.

Piemēram, ja atšķirība ir uzrakstīta uz tāfeles a-b, tad skolotājs to neteiks a ir mazais, un b- pašrisks. Viņš abus mainīgos nosauks par vienu kopīgu vārdu - noteikumiem. Un viss formas izteiksmes dēļ a-b matemātiķis redz, kā summa a + (-b). Šajā gadījumā izteiksme kļūst par summu un mainīgajiem a Un (-b) kļūt par sastāvdaļām.

Līdzīgi termini

Līdzīgi termini ir termini, kuriem ir viena burta daļa. Piemēram, apsveriet izteiksmi 7a + 6b + 2a. Noteikumi 7.a Un 2a ir tāda pati burta daļa - mainīgais a. Tātad noteikumi 7.a Un 2a ir līdzīgi.

Parasti līdzīgi termini tiek pievienoti, lai vienkāršotu izteiksmi vai atrisinātu vienādojumu. Šo operāciju sauc līdzīgu terminu samazināšana.

Lai iegūtu līdzīgus terminus, jums jāsaskaita šo terminu koeficienti un rezultāts jāreizina ar kopējo burtu daļu.

Piemēram, izteiksmē mēs sniedzam līdzīgus terminus 3a + 4a + 5a. Šajā gadījumā visi termini ir līdzīgi. Mēs saskaitām to koeficientus un reizinim rezultātu ar kopējo burtu daļu - ar mainīgo a

3a + 4a + 5a = (3 + 4 + 5) × a = 12a

Šādi termini parasti tiek doti prātā, un rezultāts tiek ierakstīts nekavējoties:

3a + 4a + 5a = 12a

Varat arī strīdēties šādi:

Bija 3 mainīgie a, tiem tika pievienoti vēl 4 mainīgie a un vēl 5 mainīgie a. Rezultātā mēs saņēmām 12 mainīgos a

Apskatīsim vairākus līdzīgu terminu samazināšanas piemērus. Ņemot vērā, ka šī tēma ir ļoti svarīga, sākumā mēs detalizēti pierakstīsim katru detaļu. Neskatoties uz to, ka šeit viss ir ļoti vienkārši, lielākā daļa cilvēku pieļauj daudz kļūdu. Lielākoties neuzmanības, nevis nezināšanas dēļ.

1. piemērs 3a + 2a + 6a + 8 a

Mēs pievienojam koeficientus šai izteiksmei un reizinim rezultātu ar kopējo burtu daļu:

3a + 2a + 6a + 8a = (3 + 2 + 6 + 8) × a = 19a

dizains (3 + 2 + 6 + 8) × a jūs nevarat pierakstīt, tāpēc mēs nekavējoties pierakstīsim atbildi

3a + 2a + 6a + 8a = 19a

2. piemērs Izteicienā iekļaujiet līdzīgus terminus 2a+a

Otrais termiņš a rakstīts bez koeficienta, bet patiesībā pirms tā ir koeficients 1 , ko mēs neredzam tāpēc, ka tas nav ierakstīts. Tātad izteiksme izskatās šādi:

2a + 1a

Tagad mēs piedāvājam līdzīgus terminus. Tas ir, mēs pievienojam koeficientus un reizinim rezultātu ar kopējo burtu daļu:

2a + 1a = (2 + 1) × a = 3a

Īsi uzrakstīsim risinājumu:

2a + a = 3a

2a+a, jūs varat strīdēties citā veidā:

3. piemērs Izteicienā iekļaujiet līdzīgus terminus 2a - a

Aizstāsim atņemšanu ar saskaitīšanu:

2a + (–a)

Otrais termiņš (-a) rakstīts bez koeficienta, bet patiesībā tā izskatās (-1a). Koeficients −1 atkal neredzams, jo tas nav ierakstīts. Tātad izteiksme izskatās šādi:

2a + (-1a)

Tagad mēs piedāvājam līdzīgus terminus. Mēs pievienojam koeficientus un reizinim rezultātu ar kopējo burtu daļu:

2a + (-1a) = (2 + (-1)) × a = 1a = a

Parasti raksta īsāk:

2a − a = a

Līdzīgu terminu iekļaušana izteiksmē 2a-a Varat arī strīdēties citā veidā:

Bija 2 mainīgie a , tika atņemts viens mainīgais a , kā rezultātā bija tikai viens mainīgais a

4. piemērs Izteicienā iekļaujiet līdzīgus terminus 6a - 3a + 4a - 8a

6a - 3a + 4a - 8a = 6a + (-3a) + 4a + (-8a)

Tagad mēs piedāvājam līdzīgus terminus. Mēs saskaitām koeficientus un reizinim rezultātu ar kopējo burtu daļu

(6 + (−3) + 4 + (−8)) × a = −1a = −a

Īsi uzrakstīsim risinājumu:

6a - 3a + 4a - 8a = -a

Ir izteicieni, kas satur vairākas dažādas līdzīgu terminu grupas. Piemēram, 3a + 3b + 7a + 2b. Uz šādām izteiksmēm attiecas tie paši noteikumi, kas uz pārējām, proti, saskaitot koeficientus un reizinot rezultātu ar kopējo burtu daļu. Bet, lai izvairītos no kļūdām, dažādas terminu grupas ir ērti pasvītrot ar dažādām līnijām.

Piemēram, izteiksmē 3a + 3b + 7a + 2b tie termini, kas satur mainīgo a, var pasvītrot ar vienu rindiņu, un tie termini, kas satur mainīgo b, var pasvītrot ar divām rindiņām:

Tagad mēs varam ieviest līdzīgus noteikumus. Tas ir, pievienojiet koeficientus un reiziniet rezultātu ar kopējo burtu daļu. Tas jādara abām terminu grupām: terminiem, kas satur mainīgo a un terminiem, kas satur mainīgo b.

3a + 3b + 7a + 2b = (3+7) ×a + (3 + 2) × b = 10a + 5b

Atkal, mēs atkārtojam, izteiksme ir vienkārša, un līdzīgus terminus var dot prātā:

3a + 3b + 7a + 2b = 10a + 5b

5. piemērs Izteicienā iekļaujiet līdzīgus terminus 5a - 6a - 7b + b

Ja iespējams, mēs aizstājam atņemšanu ar saskaitīšanu:

5a − 6a −7b + b = 5a + (−6a) + (−7b) + b

Pasvītrojiet līdzīgus terminus ar dažādām līnijām. Termini, kas satur mainīgos a pasvītrot ar vienu rindiņu, un termini saturs ir mainīgie b, pasvītrots ar divām rindiņām:

Tagad mēs varam ieviest līdzīgus noteikumus. Tas ir, pievienojiet koeficientus un reiziniet rezultātu ar kopējo burtu daļu:

5a + (−6a) + (−7b) + b = (5 + (−6)) × a + ((−7) + 1) × b = −a + (−6b)

Ja izteiksmē ir parastie skaitļi bez alfabētiskajiem faktoriem, tie tiek pievienoti atsevišķi.

6. piemērs Izteicienā iekļaujiet līdzīgus terminus 4a + 3a - 5 + 2b + 7

Ja iespējams, aizstāsim atņemšanu ar saskaitīšanu:

4a + 3a - 5 + 2b + 7 = 4a + 3a + (-5) + 2b + 7

Piedāvāsim līdzīgus terminus. Skaitļi −5 Un 7 nav burtiski faktori, bet tie ir līdzīgi termini - jums tie vienkārši jāsaskaita. Un termins 2b paliks nemainīgs, jo tas ir vienīgais šajā izteiksmē, kam ir burtu faktors b, un tam nav ko pievienot:

4a + 3a + (−5) + 2b + 7 = (4 + 3) × a + 2b + (−5) + 7 = 7a + 2b + 2

Īsi uzrakstīsim risinājumu:

4a + 3a - 5 + 2b + 7 = 7a + 2b + 2

Terminus var pasūtīt tā, lai tie termini, kuriem ir viena burta daļa, atrastos vienā un tajā pašā izteiksmes daļā.

7. piemērs Izteicienā iekļaujiet līdzīgus terminus 5t+2x+3x+5t+x

Tā kā izteiksme ir vairāku terminu summa, tas ļauj mums to novērtēt jebkurā secībā. Tāpēc termini, kas satur mainīgo t, var rakstīt izteiksmes sākumā un terminus, kas satur mainīgo x izteiksmes beigās:

5t+5t+2x+3x+x

Tagad mēs varam pievienot līdzīgus terminus:

5t + 5t + 2x + 3x + x = (5+5) × t + (2+3+1) × x = 10t + 6x

Īsi uzrakstīsim risinājumu:

5t + 2x + 3x + 5t + x = 10t + 6x

Pretējo skaitļu summa ir nulle. Šis noteikums darbojas arī burtiskām izteiksmēm. Ja izteiksmē ir tie paši termini, bet ar pretējas zīmes, tad tos var novērst līdzīgu terminu samazināšanas stadijā. Citiem vārdiem sakot, vienkārši izmetiet tos no izteiksmes, jo to summa ir nulle.

8. piemērs Izteicienā iekļaujiet līdzīgus terminus 3t - 4t - 3t + 2t

Ja iespējams, aizstāsim atņemšanu ar saskaitīšanu:

3t - 4t - 3t + 2t = 3t + (-4t) + (-3t) + 2t

Noteikumi 3t Un (-3t) ir pretēji. Pretēju vārdu summa ir vienāda ar nulli. Ja mēs noņemsim šo nulli no izteiksmes, tad izteiksmes vērtība nemainīsies, tāpēc mēs to noņemsim. Un mēs to noņemsim ar parasto noteikumu dzēšanu 3t Un (-3t)

Rezultātā mums būs izteiksme (−4t) + 2t. Šajā izteiksmē varat pievienot līdzīgus vārdus un iegūt galīgo atbildi:

(−4t) + 2t = ((−4) + 2) × t = −2t

Īsi uzrakstīsim risinājumu:

Izteiksmes vienkāršošana

"vienkāršo izteicienu" un tālāk ir jāvienkāršo izteiksme. Vienkāršojiet izteiksmi nozīmē padarīt to vienkāršāku un īsāku.

Faktiski mēs jau esam nodarbojušies ar izteiksmju vienkāršošanu, samazinot daļskaitļus. Pēc samazināšanas frakcija kļuva īsāka un vieglāk lasāma.

Apsveriet šādu piemēru. Vienkāršojiet izteiksmi.

Šo uzdevumu burtiski var saprast šādi: "Dariet visu, ko varat darīt ar šo izteiksmi, bet padariet to vienkāršāku" .

Šajā gadījumā jūs varat samazināt daļskaitli, proti, dalīt daļas skaitītāju un saucēju ar 2:

Ko vēl var darīt? Jūs varat aprēķināt iegūto daļu. Tad mēs iegūstam decimāldaļu 0,5

Rezultātā frakcija tika vienkāršota līdz 0,5.

Pirmajam jautājumam, kas jāuzdod sev, risinot šādas problēmas, vajadzētu būt "ko var darīt?" . Jo ir lietas, ko vari darīt, un ir lietas, ko nevari.

Cits svarīgs punkts Jāpatur prātā, ka izteiksmes vērtība nedrīkst mainīties pēc izteiksmes vienkāršošanas. Atgriezīsimies pie izteiciena. Šī izteiksme ir dalījums, ko var izpildīt. Pēc šīs dalīšanas mēs iegūstam šīs izteiksmes vērtību, kas ir vienāda ar 0,5

Bet mēs vienkāršojām izteiksmi un ieguvām jaunu vienkāršotu izteiksmi. Jaunās vienkāršotās izteiksmes vērtība joprojām ir 0,5

Bet mēs arī mēģinājām vienkāršot izteiksmi, to aprēķinot. Rezultātā galīgā atbilde bija 0,5.

Tādējādi neatkarīgi no tā, kā mēs vienkāršojam izteiksmi, iegūto izteiksmju vērtība joprojām ir 0,5. Tas nozīmē, ka vienkāršošana katrā posmā tika veikta pareizi. Tas ir tas, uz ko mums jātiecas, vienkāršojot izteicienus - izteiciena nozīmei nevajadzētu ciest no mūsu darbībām.

Bieži vien ir jāvienkāršo burtiski izteicieni. Uz tiem attiecas tie paši vienkāršošanas noteikumi kā uz skaitliskām izteiksmēm. Varat veikt jebkuru derīgu darbību, ja vien izteiksmes vērtība nemainās.

Apskatīsim dažus piemērus.

1. piemērs Vienkāršojiet izteiksmi 5,21 s × t × 2,5

Lai vienkāršotu šo izteiksmi, varat reizināt ciparus atsevišķi un burtus atsevišķi. Šis uzdevums ir ļoti līdzīgs tam, ko mēs apsvērām, kad mācījāmies noteikt koeficientu:

5,21 s × t × 2,5 = 5,21 × 2,5 × s × t = 13,025 × st = 13,025 st

Tātad izteiksme 5,21 s × t × 2,5 vienkāršots līdz 13.025.

2. piemērs Vienkāršojiet izteiksmi −0,4×(−6,3b)×2

Otrais darbs (−6.3b) var pārtulkot mums saprotamā formā, proti, rakstīt formā ( −6,3) × b , tad atsevišķi reiziniet ciparus un atsevišķi reiziniet burtus:

− 0,4 × (−6.3b) × 2 = − 0,4 × (−6,3) × b × 2 = 5,04b

Tātad izteiksme −0,4×(−6,3b)×2 vienkāršots līdz 5.04b

3. piemērs Vienkāršojiet izteiksmi

Uzrakstīsim šo izteiksmi sīkāk, lai skaidri redzētu, kur atrodas cipari un kur burti:

Tagad mēs reizinām ciparus atsevišķi un reizinām burtus atsevišķi:

Tātad izteiksme vienkāršots līdz −abc.Šo risinājumu var uzrakstīt īsāk:

Vienkāršojot izteiksmes, daļskaitļus var samazināt risināšanas procesā, nevis pašās beigās, kā mēs to darījām ar parastās frakcijas. Piemēram, ja risināšanas laikā sastopamies ar formas izteiksmi, tad nemaz nav nepieciešams aprēķināt skaitītāju un saucēju un rīkoties šādi:

Daļu var samazināt, izvēloties gan koeficientu skaitītājā, gan saucējā un samazinot šos faktorus ar to lielāko kopīgo dalītāju. Citiem vārdiem sakot, izmantojiet , kurā mēs detalizēti neaprakstām, kā tika sadalīts skaitītājs un saucējs.

Piemēram, skaitītājā koeficientu 12 un saucējā koeficientu 4 var samazināt par 4. Paturam prātā četrinieku un, dalot 12 un 4 ar šo četrinieku, rakstam atbildes pie šiem skaitļiem, ņemot vērā iepriekš tos izsvītroja

Tagad jūs varat reizināt iegūtos mazos faktorus. Šajā gadījumā to nav daudz, un jūs varat tos pavairot savā prātā:

Ar laiku var atklāties, ka, risinot kādu konkrētu problēmu, izteicieni sāk “pabiezēt”, tāpēc vēlams pierast pie ātriem aprēķiniem. Tas, ko var aprēķināt prātā, ir jāaprēķina prātā. To, ko var ātri nogriezt, vajadzētu ātri nogriezt.

4. piemērs Vienkāršojiet izteiksmi

Tātad izteiksme vienkāršots līdz

5. piemērs Vienkāršojiet izteiksmi

Mēs reizinām ciparus atsevišķi un burtus atsevišķi:

Tātad izteiksme vienkāršots līdz mn.

6. piemērs Vienkāršojiet izteiksmi

Uzrakstīsim šo izteiksmi sīkāk, lai skaidri redzētu, kur atrodas cipari un kur burti:

Tagad mēs reizinām ciparus atsevišķi un burtus atsevišķi. Aprēķinu ērtībai decimāldaļdaļa −6,4 un jaukts numurs var pārvērst parastajās daļās:

Tātad izteiksme vienkāršots līdz

Šī piemēra risinājumu var uzrakstīt daudz īsāk. Tas izskatīsies šādi:

7. piemērs Vienkāršojiet izteiksmi

Mēs reizinām ciparus atsevišķi un burtus atsevišķi. Aprēķinu ērtībai jauktos skaitļus un decimāldaļas 0,1 un 0,6 var pārvērst parastajās daļās:

Tātad izteiksme vienkāršots līdz abcd. Ja izlaižat detaļas, šo risinājumu var uzrakstīt daudz īsāk:

Ievērojiet, kā daļa ir samazināta. Var samazināt arī jaunus reizinātājus, kas iegūti, samazinot iepriekšējos reizinātājus.

Tagad parunāsim par to, ko nevajadzētu darīt. Vienkāršojot izteiksmes, stingri aizliegts reizināt ciparus un burtus, ja izteiksme ir summa, nevis reizinājums.

Piemēram, ja vēlaties vienkāršot izteiksmi 5a + 4b, tad to nevar rakstīt šādi:

Tas ir līdzvērtīgs faktam, ka, ja mums lūgtu pievienot divus skaitļus, mēs tos reizinātu, nevis pievienotu.

Aizstājot jebkuras mainīgo vērtības a Un b izteiksme 5a+4b pārvēršas par vienkāršu skaitlisku izteiksmi. Pieņemsim mainīgos a Un b ir šādas nozīmes:

a = 2, b = 3

Tad izteiksmes vērtība būs 22

5a + 4b = 5 × 2 + 4 × 3 = 10 + 12 = 22

Vispirms tiek veikta reizināšana, un pēc tam rezultāti tiek pievienoti. Un, ja mēs mēģinātu vienkāršot šo izteiksmi, reizinot ciparus un burtus, mēs iegūtu sekojošo:

5a + 4b = 5 × 4 × a × b = 20ab

20ab = 20 x 2 x 3 = 120

Izrādās pavisam cita izteiciena nozīme. Pirmajā gadījumā tas izrādījās 22 , otrajā gadījumā 120 . Tas nozīmē, ka izteiksmes vienkāršošana 5a + 4b tika veikta nepareizi.

Pēc izteiksmes vienkāršošanas tās vērtība nedrīkst mainīties ar vienādām mainīgo vērtībām. Ja, aizstājot jebkuru mainīgo vērtību sākotnējā izteiksmē, tiek iegūta viena vērtība, tad pēc izteiksmes vienkāršošanas jāiegūst tāda pati vērtība kā pirms vienkāršošanas.

Ar izteiksmi 5a + 4b patiesībā neko nevar izdarīt. Vieglāk nekļūst.

Ja izteiksmē ir līdzīgi termini, tos var pievienot, ja mūsu mērķis ir vienkāršot izteiksmi.

8. piemērs Vienkāršojiet izteiksmi 0,3a–0,4a+a

0,3a - 0,4a + a = 0,3a + (-0,4a) + a = (0,3 + (-0,4) + 1) × a = 0,9a

vai īsāks: 0,3a - 0,4a + a = 0.9a

Tātad izteiksme 0,3a–0,4a+a vienkāršots līdz 0.9a

9. piemērs Vienkāršojiet izteiksmi −7,5a − 2,5b + 4a

Lai vienkāršotu šo izteiksmi, varat pievienot līdzīgus terminus:

−7.5a − 2.5b + 4a = −7.5a + (−2.5b) + 4a = ((−7.5) + 4)×a + (−2.5b) = −3.5a + (−2.5b)

vai īsāks −7.5a − 2.5b + 4a = −3.5a + (−2.5b)

jēdziens (−2,5 b) palika nemainīgs, jo nebija ar ko to salocīt.

10. piemērs Vienkāršojiet izteiksmi

Lai vienkāršotu šo izteiksmi, varat pievienot līdzīgus terminus:

Koeficients bija aprēķina ērtībai.

Tātad izteiksme vienkāršots līdz

11. piemērs. Vienkāršojiet izteiksmi

Lai vienkāršotu šo izteiksmi, varat pievienot līdzīgus terminus:

Tātad izteiksme vienkāršots līdz .

IN šis piemērs saprātīgāk būtu vispirms pievienot pirmo un pēdējo koeficientu. Šajā gadījumā mēs iegūtu īsu risinājumu. Tas izskatītos šādi:

12. piemērs. Vienkāršojiet izteiksmi

Lai vienkāršotu šo izteiksmi, varat pievienot līdzīgus terminus:

Tātad izteiksme vienkāršots līdz .

Termins palika nemainīgs, jo tam nebija ko pievienot.

Šo risinājumu var uzrakstīt daudz īsāk. Tas izskatīsies šādi:

Īsajā risinājumā nav iekļautas darbības, kas paredz atņemšanas aizstāšanu ar saskaitīšanu, un detalizēts ieraksts par to, kā daļskaitļi tika samazināti līdz kopsaucējam.

Vēl viena atšķirība ir tā, ka iekšā detalizēts risinājums atbilde izskatās , bet īsumā kā . Patiesībā tas ir tas pats izteiciens. Atšķirība ir tāda, ka pirmajā gadījumā atņemšana tiek aizstāta ar saskaitīšanu, jo sākumā, kad mēs rakstījām risinājumu detalizēts skats, mēs esam aizstājuši atņemšanu ar saskaitīšanu, kur vien iespējams, un šī aizstāšana ir saglabāta atbildei.

Identitātes. Identiskas vienādas izteiksmes

Pēc tam, kad esam vienkāršojuši jebkuru izteiksmi, tā kļūst vienkāršāka un īsāka. Lai pārbaudītu, vai izteiksme ir pareizi vienkāršota, pietiek ar jebkuru mainīgo vērtību aizstāt vispirms ar iepriekšējo izteiksmi, kas bija jāvienkāršo, un pēc tam ar jauno, kas tika vienkāršota. Ja vērtība abās izteiksmēs ir vienāda, izteiksme tiek vienkāršota pareizi.

Apsveriet vienkāršākais piemērs. Ļaujiet tai pieprasīt izteiksmes vienkāršošanu 2a × 7b. Lai vienkāršotu šo izteiksmi, varat atsevišķi reizināt ciparus un burtus:

2a × 7b = 2 × 7 × a × b = 14ab

Pārbaudīsim, vai esam pareizi vienkāršojuši izteiksmi. Lai to izdarītu, aizstājiet jebkuru mainīgo vērtību a Un b vispirms uz pirmo izteiksmi, kas bija jāvienkāršo, un pēc tam uz otro, kas tika vienkāršota.

Ļaujiet mainīgo vērtībām a , b būs šādi:

a = 4, b = 5

Aizstājiet tos pirmajā izteiksmē 2a × 7b

Tagad aizstāsim tās pašas mainīgo vērtības izteiksmē, kas izrietēja no vienkāršošanas 2a × 7b, proti, izteiksmē 14ab

14ab = 14x4x5 = 280

Mēs redzam, ka plkst a=4 Un b=5 pirmās izteiksmes vērtība 2a × 7b un otrās izteiksmes vērtību 14ab vienāds

2a × 7b = 2 × 4 × 7 × 5 = 280

14ab = 14x4x5 = 280

Tas pats notiks ar citām vērtībām. Piemēram, ļaujiet a=1 Un b=2

2a × 7b = 2 × 1 × 7 × 2 = 28

14ab = 14 x 1 x 2 = 28

Tādējādi jebkurām mainīgo vērtībām izteiksmes 2a × 7b Un 14ab ir vienādi ar to pašu vērtību. Tādus izteicienus sauc identiski vienādi.

Mēs secinām, ka starp izteicieniem 2a × 7b Un 14ab jūs varat likt vienādības zīmi, jo tās ir vienādas ar vienu un to pašu vērtību.

2a × 7b = 14ab

Vienādība ir jebkura izteiksme, kas ir savienota ar vienādības zīmi (=).

Un formas vienlīdzība 2a × 7b = 14ab sauca identitāti.

Identitāte ir vienādība, kas attiecas uz jebkuru mainīgo vērtību.

Citi identitātes piemēri:

a + b = b + a

a(b+c) = ab + ac

a(bc) = (ab)c

Jā, matemātikas likumi, kurus mēs pētījām, ir identitātes.

Patiesas skaitliskās vienādības ir arī identitātes. Piemēram:

2 + 2 = 4

3 + 3 = 5 + 1

10 = 7 + 2 + 1

Lemjot grūts uzdevums, lai atvieglotu aprēķinu, sarežģītā izteiksme tiek aizstāta ar vienkāršāku izteiksmi, kas ir identiski vienāda ar iepriekšējo. Tādu nomaiņu sauc identiska izteiksmes transformācija vai vienkārši izteiksmes konvertēšana.

Piemēram, mēs vienkāršojām izteiksmi 2a × 7b, un iegūstiet vienkāršāku izteiksmi 14ab. Šo vienkāršošanu var saukt par identitātes transformāciju.

Jūs bieži varat atrast uzdevumu, kas saka "pierādiet, ka vienlīdzība ir identitāte" un tad tiek dota pierādāmā vienlīdzība. Parasti šī vienlīdzība sastāv no divām daļām: vienādības kreisās un labās daļas. Mūsu uzdevums ir veikt identiskas pārvērtības ar vienu no vienādības daļām un iegūt otru daļu. Vai arī veiciet identiskas transformācijas ar abām vienādības daļām un pārliecinieties, ka abās vienādības daļās ir vienādas izteiksmes.

Piemēram, pierādīsim, ka vienlīdzība 0,5a × 5b = 2,5ab ir identitāte.

Vienkāršojiet šīs vienlīdzības kreiso pusi. Lai to izdarītu, reiziniet ciparus un burtus atsevišķi:

0,5 × 5 × a × b = 2,5ab

2,5ab = 2,5ab

Nelielas identiskas transformācijas rezultātā kreisā puse vienlīdzība kļuva vienāda ar vienlīdzības labo pusi. Tātad mēs esam pierādījuši, ka vienlīdzība 0,5a × 5b = 2,5ab ir identitāte.

No identiskiem pārveidojumiem mēs iemācījāmies saskaitīt, atņemt, reizināt un dalīt skaitļus, samazināt daļskaitļus, iegūt līdzīgus vārdus un arī vienkāršot dažas izteiksmes.

Bet tās ir tālu no visām identiskām transformācijām, kas pastāv matemātikā. Ir daudz vairāk identisku pārvērtību. Nākotnē mēs to redzēsim atkal un atkal.

Uzdevumi patstāvīgam risinājumam:

Vai jums patika nodarbība?
Pievienojieties mūsu jaunajai Vkontakte grupai un sāciet saņemt paziņojumus par jaunām nodarbībām

Algebrisko izteiksmju vienkāršošana ir viena no algebras apguves atslēgām un ārkārtīgi noderīga prasme visiem matemātiķiem. Vienkāršošana ļauj samazināt sarežģītu vai garu izteiksmi līdz vienkāršai izteiksmei, ar kuru ir viegli strādāt. Vienkāršošanas pamatprasmes ir labas pat tiem, kuri nav entuziasma par matemātiku. Paturot dažus vienkārši noteikumi, jūs varat vienkāršot daudzus visbiežāk sastopamos algebrisko izteiksmju veidus bez īpašām matemātikas zināšanām.

Soļi

Svarīgas definīcijas

1. Līdzīgi dalībnieki. Tie ir dalībnieki ar tādas pašas kārtas mainīgo, dalībnieki ar vienādiem mainīgajiem vai brīvie dalībnieki (dalībnieki, kas nesatur mainīgo). Citiem vārdiem sakot, līdzīgi termini ietver vienu mainīgo tādā pašā mērā, ietver vairākus identiskus mainīgos vai vispār neiekļauj mainīgo. Terminu secībai izteiksmē nav nozīmes.

   • Piemēram, 3x 2 un 4x 2 ir līdzīgi terminiem, jo ​​tie satur otrās kārtas mainīgo "x" (otrajā pakāpē). Tomēr x un x 2 nav līdzīgi dalībnieki, jo tie satur dažādu secību mainīgo "x" (pirmā un otrā). Tāpat -3yx un 5xz nav līdzīgi dalībnieki, jo tajos ir dažādi mainīgie.

2. Faktorizācija. Tas ir tādu skaitļu atrašana, kuru reizinājums noved pie sākotnējā skaitļa. Jebkuram sākotnējam skaitlim var būt vairāki faktori. Piemēram, skaitli 12 var sadalīt šādās faktoru sērijās: 1 × 12, 2 × 6 un 3 × 4, tāpēc mēs varam teikt, ka skaitļi 1, 2, 3, 4, 6 un 12 ir faktori no skaitlis 12. Koeficienti ir tādi paši kā dalītāji , tas ir, skaitļi, ar kuriem dalās sākotnējais skaitlis.

   • Piemēram, ja vēlaties faktorēt skaitli 20, ierakstiet to šādi: 4×5.
   • Ņemiet vērā, ka, veicot faktoringu, tiek ņemts vērā mainīgais. Piemēram, 20x = 4 (5 x).
   • Pirmskaitļus nevar ņemt vērā, jo tie dalās tikai ar sevi un 1.

3. Atcerieties un ievērojiet darbību secību, lai izvairītos no kļūdām.

   • Kronšteini
   • Grāds
   • Reizināšana
   • Divīzija
   • Papildinājums
   • Atņemšana

   Casting Like Members

   1. Pierakstiet izteiksmi. Vienšūņi algebriskās izteiksmes(kas nesatur frakcijas, saknes un tā tālāk) var atrisināt (vienkāršoti) tikai dažās darbībās.

      • Piemēram, vienkāršojiet izteiksmi 1 + 2x - 3 + 4x.

   2. Definējiet līdzīgus dalībniekus (dalībniekus ar tādas pašas kārtas mainīgo, dalībniekus ar vienādiem mainīgajiem vai brīvos dalībniekus).

      • Atrodiet līdzīgus terminus šajā izteiksmē. Termini 2x un 4x satur tādas pašas secības mainīgo (pirmais). Arī 1 un -3 ir bezmaksas dalībnieki (neietver mainīgo). Tādējādi šajā izteiksmē termini 2x un 4x ir līdzīgi, un dalībnieki 1 un -3 ir arī līdzīgi.

   3. Dodiet līdzīgus dalībniekus. Tas nozīmē to pievienošanu vai atņemšanu un izteiksmes vienkāršošanu.

      • 2x+4x= 6x
      • 1 - 3 = -2

   4. Pārrakstiet izteiksmi, ņemot vērā dotos terminus. Jūs saņemsiet vienkāršu izteiksmi ar mazāk terminu. Jaunā izteiksme ir vienāda ar sākotnējo.

      • Mūsu piemērā: 1 + 2x - 3 + 4x = 6x - 2, tas ir, sākotnējā izteiksme ir vienkāršota un ar to ir vieglāk strādāt.

   5. Ievērojiet secību, kādā tiek veiktas darbības, izlejot līdzīgus terminus. Mūsu piemērā bija viegli ieviest līdzīgus terminus. Tomēr sarežģītu izteicienu gadījumā, kuros dalībnieki ir ievietoti iekavās un ir klāt daļskaitļi un saknes, šādus terminus nav tik vienkārši ieviest. Šādos gadījumos ievērojiet darbību secību.

      • Piemēram, apsveriet izteiksmi 5(3x - 1) + x((2x)/(2)) + 8 - 3x. Šeit būtu kļūda uzreiz definēt 3x un 2x kā līdzīgus terminus un tos citēt, jo vispirms ir jāpaplašina iekavas. Tāpēc veiciet darbības to secībā.
        • 5(3x-1) + x((2x)/(2)) + 8 - 3x
        • 15x - 5 + x(x) + 8 - 3x
        • 15x - 5 + x 2 + 8 - 3x. Tagad, ja izteiksmē ir ietvertas tikai saskaitīšanas un atņemšanas darbības, varat nodot līdzīgus terminus.
        • x 2 + (15x - 3x) + (8 - 5)
        • x 2 + 12x + 3

   Reizinātāja ievietošana iekavās

   1. Atrodiet visu izteiksmes koeficientu lielāko kopīgo dalītāju (gcd). GCD ir lielākais skaitlis, ar kuru dalās visi izteiksmes koeficienti.

      • Piemēram, apsveriet vienādojumu 9x 2 + 27x - 3. Šajā gadījumā gcd=3, jo jebkurš šīs izteiksmes koeficients dalās ar 3.

   2. Sadaliet katru izteiksmes terminu ar gcd. Iegūtie termini saturēs mazākus koeficientus nekā sākotnējā izteiksmē.

      • Mūsu piemērā katru izteiksmes vienumu sadaliet ar 3.
        • 9x2/3=3x2
        • 27x/3=9x
        • -3/3 = -1
        • Izrādījās izteiksme 3x2 + 9x-1. Tas nav vienāds ar sākotnējo izteiksmi.

   3. Uzrakstiet sākotnējo izteiksmi kā vienādu ar gcd reizinājumu ar iegūto izteiksmi. Tas ir, ievietojiet iegūto izteiksmi iekavās un izlieciet GCD no iekavām.

      • Mūsu piemērā: 9x 2 + 27x - 3 = 3 (3 x 2 + 9 x - 1)

   4. Daļskaitļu izteiksmju vienkāršošana, izņemot reizinātāju no iekavām. Kāpēc vienkārši izņemt reizinātāju no iekavām, kā tas tika darīts iepriekš? Pēc tam, lai uzzinātu, kā vienkāršot sarežģītas izteiksmes, piemēram, daļskaitļus. Šajā gadījumā faktora izlikšana no iekavām var palīdzēt atbrīvoties no daļskaitļa (no saucēja).

      • Piemēram, apsveriet daļskaitļu izteiksmi (9x 2 + 27x - 3)/3. Izmantojiet iekavas, lai vienkāršotu šo izteiksmi.
        • Izņemiet koeficientu 3 (kā jūs to darījāt iepriekš): (3(3x 2 + 9x - 1))/3
        • Ņemiet vērā, ka gan skaitītājam, gan saucējam tagad ir skaitlis 3. To var samazināt, un jūs saņemsiet izteiksmi: (3x 2 + 9x - 1) / 1
        • Tā kā jebkura daļa, kuras saucējā ir skaitlis 1, ir vienāda ar skaitītāju, sākotnējā daļskaitļa izteiksme tiek vienkāršota līdz: 3x2 + 9x-1.

   Papildu vienkāršošanas metodes

4. Apsveriet vienkāršu piemēru: √(90). Skaitli 90 var sadalīt šādos faktoros: 9 un 10 un no 9 ekstrakts Kvadrātsakne(3) un izņemiet 3 no zem saknes.
   • √(90)
   • √ (9 × 10)
   • √(9) × √(10)
   • 3×√(10)
   • 3√(10)

5. Izteicienu vienkāršošana ar pilnvarām. Dažās izteiksmēs ir terminu reizināšanas vai dalīšanas darbības ar pakāpi. Ja termini tiek reizināti ar vienu bāzi, to pakāpes tiek saskaitītas; dalot terminus ar vienu un to pašu bāzi, to pakāpes tiek atņemtas.

   • Piemēram, apsveriet izteiksmi 6x 3 × 8x 4 + (x 17 / x 15). Reizināšanas gadījumā saskaitiet eksponentus, bet dalīšanas gadījumā atņemiet tos.
     • 6 x 3 x 8 x 4 + (x 17/x15)
     • (6 × 8) x 3 + 4 + (x 17–15)
     • 48x7+x2
   • Tālāk ir sniegts noteikumu skaidrojums par terminu reizināšanu un dalīšanu ar pakāpi.
     • Vārdu reizināšana ar pilnvarām ir līdzvērtīga terminu reizināšanai ar sevi. Piemēram, tā kā x 3 = x × x × x un x 5 = x × x × x × x × x, tad x 3 × x 5 = (x × x × x) × (x × x × x × x × x), vai x 8 .
     • Tāpat terminu sadalīšana ar pilnvarām ir līdzvērtīga terminu dalīšanai ar sevi. x 5 /x 3 \u003d (x × x × x × x × x) / (x × x × x). Tā kā līdzīgus vārdus, kas ir gan skaitītājā, gan saucējā, var samazināt, divu "x" vai x 2 reizinājums paliek skaitītājā.

• Vienmēr ievērojiet zīmes (plus vai mīnus) pirms izteiksmes terminiem, jo ​​daudziem cilvēkiem ir grūtības izvēlēties pareizo zīmi.
• Lūdziet palīdzību, ja nepieciešams!
• Algebrisko izteiksmju vienkāršošana nav vienkārša, taču, ja jūs to paņemat, jūs varat izmantot šo prasmi visu mūžu.

Jebkurā valodā var izteikt vienu un to pašu informāciju dažādi vārdi un apgrozījumu. Matemātiskā valoda nav izņēmums. Taču vienu un to pašu izteiksmi var līdzvērtīgi uzrakstīt dažādos veidos. Un dažās situācijās viens no ierakstiem ir vienkāršāks. Šajā nodarbībā mēs runāsim par izteicienu vienkāršošanu.

Cilvēki sazinās tālāk dažādās valodās. Mums svarīgs salīdzinājums ir pāris "krievu valoda - matemātiskā valoda". To pašu informāciju var sniegt dažādās valodās. Bet turklāt vienā valodā to var izrunāt atšķirīgi.

Piemēram: “Pēteris ir draugs ar Vasju”, “Vasja ir draugs ar Petju”, “Pēteris un Vasja ir draugi”. Saka savādāk, bet viens un tas pats. Izmantojot jebkuru no šīm frāzēm, mēs saprastu, kas ir uz spēles.

Apskatīsim šo frāzi: "Zēns Petja un zēns Vasja ir draugi." Mēs saprotam, ko jautājumā. Tomēr mums nepatīk, kā šī frāze skan. Vai mēs nevaram to vienkāršot, pateikt to pašu, bet vienkāršāk? "Zēns un zēns" - jūs varat teikt vienreiz: "Zēni Petja un Vasja ir draugi."

"Zēni" ... Vai pēc viņu vārdiem nav skaidrs, ka viņi nav meitenes. Mēs noņemam "zēnus": "Petja un Vasja ir draugi." Un vārdu "draugi" var aizstāt ar "draugiem": "Petja un Vasja ir draugi." Rezultātā pirmā, garā, neglītā frāze tika aizstāta ar līdzvērtīgu apgalvojumu, ko ir vieglāk pateikt un vieglāk saprast. Mēs esam vienkāršojuši šo frāzi. Vienkāršot nozīmē pateikt vieglāk, bet nezaudēt, nesagrozīt nozīmi.

Tas pats notiek matemātiskajā valodā. To pašu var teikt dažādi. Ko nozīmē izteiksmes vienkāršošana? Tas nozīmē, ka oriģinālajai izteiksmei ir daudz līdzvērtīgu izteicienu, tas ir, tie, kas nozīmē vienu un to pašu. Un no visa šī daudzuma mums jāizvēlas visvienkāršākais, mūsuprāt, vai vispiemērotākais mūsu tālākajiem mērķiem.

Piemēram, apsveriet skaitlisku izteiksmi. Tas būs līdzvērtīgs .

Tas būs arī līdzvērtīgs pirmajiem diviem: .

Izrādās, ka mēs esam vienkāršojuši savus izteicienus un atraduši īsāko ekvivalentu izteiksmi.

Skaitliskām izteiksmēm jums vienmēr ir jādara viss darbs un līdzvērtīga izteiksme jāiegūst kā viens skaitlis.

Apsveriet burtiskas izteiksmes piemēru . Acīmredzot tas būs vienkāršāk.

Vienkāršojot burtiskās izteiksmes, jums jāveic visas iespējamās darbības.

Vai vienmēr ir jāvienkāršo izteiksme? Nē, reizēm mums ērtāks būs līdzvērtīgs, bet garāks apzīmējums.

Piemērs: atņemiet skaitli no skaitļa.

Var aprēķināt, bet, ja pirmais skaitlis būtu attēlots ar tā ekvivalentu apzīmējumu: , tad aprēķini būtu momentāni: .

Tas ir, vienkāršota izteiksme mums ne vienmēr ir izdevīga turpmākiem aprēķiniem.

Tomēr ļoti bieži mēs saskaramies ar uzdevumu, kas izklausās tikai kā "vienkāršojiet izteiksmi".

Vienkāršojiet izteicienu: .

Risinājums

1) Veiciet darbības pirmajā un otrajā iekavā: .

2) Aprēķiniet produktus: .

Acīmredzot pēdējai izteiksmei ir vienkāršāka forma nekā sākotnējai. Mēs to esam vienkāršojuši.

Lai vienkāršotu izteiksmi, tas jāaizstāj ar ekvivalentu (vienāds).

Lai noteiktu līdzvērtīgu izteiksmi, jums ir:

1) veikt visas iespējamās darbības,

2) izmantot saskaitīšanas, atņemšanas, reizināšanas un dalīšanas īpašības, lai vienkāršotu aprēķinus.

Saskaitīšanas un atņemšanas īpašības:

1. Saskaitīšanas komutatīva īpašība: summa nemainās no terminu pārkārtošanas.

2. Saskaitīšanas asociatīvā īpašība: lai divu skaitļu summai pievienotu trešo skaitli, pirmajam skaitlim var pievienot otrā un trešā skaitļa summu.

3. Īpašība atņemt summu no skaitļa: lai atņemtu summu no skaitļa, jūs varat atņemt katru terminu atsevišķi.

Reizināšanas un dalīšanas īpašības

1. Reizināšanas komutatīvā īpašība: reizinājums nemainās no faktoru permutācijas.

2. Asociatīvā īpašība: lai reizinātu skaitli ar divu skaitļu reizinājumu, vispirms to var reizināt ar pirmo koeficientu un pēc tam iegūto reizinājumu ar otro koeficientu.

3. Reizināšanas sadales īpašība: lai reizinātu skaitli ar summu, tas jāreizina ar katru vārdu atsevišķi.

Apskatīsim, kā mēs faktiski veicam garīgos aprēķinus.

Aprēķināt:

Risinājums

1) Iedomājieties, kā

2) Pirmo reizinātāju attēlosim kā bitu vārdu summu un veiksim reizināšanu:

3) varat iedomāties, kā un veikt reizināšanu:

4) Aizstāt pirmo koeficientu ar ekvivalentu summu:

Sadales likumu var izmantot arī pretējā virzienā: .

Veiciet tālāk norādītās darbības.

1) 2)

Risinājums

1) Ērtības labad varat izmantot izplatīšanas likumu, tikai izmantojiet to pretējā virzienā - izņemiet kopējo koeficientu no iekavām.

2) Izņemsim kopējo koeficientu no iekavām

Virtuvē un gaitenī nepieciešams iegādāties linoleju. Virtuves zona - gaitenis -. Ir trīs veidu linoleji: par un rubļi par. Cik būs katrs no trīs veidi linolejs? (1. att.)

Rīsi. 1. Problēmas stāvokļa ilustrācija

Risinājums

1. metode. Varat atsevišķi noskaidrot, cik daudz naudas būs nepieciešams, lai virtuvē iegādātos linoleju, un pēc tam pievienot to gaitenī un saskaitīt iegūtos darbus.

Zināms, ka matemātikā nevar iztikt bez izteiksmju vienkāršošanas. Tas ir nepieciešams pareizai un ātrs lēmums dažādas problēmas, kā arī dažāda veida vienādojumi. Pārrunātā vienkāršošana nozīmē mērķa sasniegšanai nepieciešamo darbību skaita samazināšanu. Rezultātā aprēķini tiek ievērojami atviegloti, un laiks tiek ievērojami ietaupīts. Bet kā vienkāršot izteiksmi? Šim nolūkam tiek izmantotas noteiktas matemātiskās attiecības, ko bieži dēvē par formulām vai likumiem, kas ļauj izteiksmes padarīt daudz īsākas, tādējādi vienkāršojot aprēķinus.

Nav noslēpums, ka mūsdienās nav grūti vienkāršot izteicienu tiešsaistē. Šeit ir saites uz dažām populārākajām vietnēm:

Tomēr tas nav iespējams ar katru izteiksmi. Tāpēc mēs sīkāk apsvērsim tradicionālākas metodes.

Kopējā dalītāja izņemšana

Gadījumā, ja vienā izteiksmē ir monomi, kuriem ir vienādi faktori, ar tiem var atrast koeficientu summu un pēc tam reizināt ar tiem kopējo koeficientu. Šo darbību sauc arī par "kopējā dalītāja atņemšanu". Konsekventi lietojot šī metode, dažreiz ir iespējams ievērojami vienkāršot izteiksmi. Galu galā algebra kopumā ir balstīta uz faktoru un dalītāju grupēšanu un pārgrupēšanu.

Vienkāršākās formulas saīsinātai reizināšanai

Viena no iepriekš aprakstītās metodes sekām ir reducētās reizināšanas formulas. Kā ar viņu palīdzību vienkāršot izteiksmes, tas ir daudz skaidrāk tiem, kuri šīs formulas pat nav iemācījušies no galvas, bet zina, kā tās ir atvasinātas, proti, no kurienes tās nāk, un attiecīgi arī to matemātisko raksturu. Iepriekšējais apgalvojums principā paliek spēkā visā mūsdienu matemātikā, sākot no pirmās klases līdz Mehānikas un matemātikas nodaļu augstākajiem kursiem. Kvadrātu starpība, starpības un summas kvadrāts, kubu summa un starpība - visas šīs formulas plaši izmanto elementārajā, kā arī augstākajā matemātikā, gadījumos, kad uzdevumu risināšanai nepieciešams vienkāršot izteiksmi. . Šādu transformāciju piemērus var viegli atrast jebkurā skolas mācību grāmatā par algebru vai, vēl vienkāršāk, globālajā tīmeklī.

Pakāpju saknes

Elementārā matemātika, ja paskatās uz to kopumā, ir bruņota ar ne tik daudziem veidiem, kā jūs varat vienkāršot izteiksmi. Grādi un darbības ar tiem, kā likums, lielākajai daļai studentu ir salīdzinoši viegli. Tikai tagad daudziem mūsdienu skolēniem un studentiem ir ievērojamas grūtības, kad ir nepieciešams vienkāršot izteicienu ar saknēm. Un tas ir pilnīgi nepamatoti. Jo sakņu matemātiskais raksturs neatšķiras no to pašu pakāpju rakstura, ar kurām parasti ir daudz mazāk grūtību. Ir zināms, ka skaitļa, mainīgā vai izteiksmes kvadrātsakne nav nekas cits kā tas pats skaitlis, mainīgais vai izteiksme ar pakāpi "viena sekunde", kuba sakne ir tāda pati ar "vienas trešdaļas" pakāpi, un tā sarakstes ceļā.

Izteikumu vienkāršošana ar daļskaitļiem

Apsveriet arī izplatītu piemēru, kā vienkāršot izteiksmi ar daļskaitļiem. Gadījumos, kad izteicieni ir dabiskās frakcijas, no saucēja un skaitītāja jāizvēlas kopīgs koeficients un pēc tam jāsamazina daļa par to. Ja monomiāļiem ir vienādi reizinātāji, kas palielināti pakāpēs, ir jāuzrauga pakāpju vienlīdzība, tos summējot.

Vienkāršāko trigonometrisko izteiksmju vienkāršošana

Daži atsevišķi ir saruna par to, kā vienkāršot trigonometrisko izteiksmi. Visplašākā trigonometrijas sadaļa, iespējams, ir pirmais posms, kurā matemātikas studenti saskarsies ar nedaudz abstraktiem jēdzieniem, problēmām un to risināšanas metodēm. Šeit ir atbilstošas ​​formulas, no kurām pirmā ir pamata trigonometriskā identitāte. Ar pietiekamu matemātisku domāšanas veidu var izsekot visu galveno identitātes sistemātiskai atvasināšanai no šīs identitātes trigonometriskās identitātes un formulas, tostarp formulas argumentu atšķirībai un summai, dubultie, trīskāršie argumenti, samazināšanas formulas un daudzas citas. Protams, šeit nevajadzētu aizmirst pašas pirmās metodes, piemēram, kopējā faktora izņemšanu, kas tiek pilnībā izmantotas kopā ar jaunām metodēm un formulām.

Apkopojot, šeit ir daži vispārīgi padomi lasītājam:

• Polinomi ir jāfaktorē, tas ir, tie ir jāatspoguļo noteikta skaita faktoru reizinājuma formā - monomiāli un polinomi. Ja ir tāda iespēja, ir nepieciešams izņemt kopējo faktoru no iekavām.
• Labāk ir iegaumēt visas saīsinātās reizināšanas formulas bez izņēmuma. To nav tik daudz, bet tie ir pamats matemātisko izteiksmju vienkāršošanai. Nedrīkst aizmirst arī par perfektu kvadrātu izcelšanas metodi trinomiālos, kas ir apgrieztā darbība vienai no saīsinātajām reizināšanas formulām.
• Visas esošās daļas izteiksmē ir jāsamazina pēc iespējas biežāk. To darot, neaizmirstiet, ka tiek samazināti tikai reizinātāji. Kad saucējs un skaitītājs algebriskās daļas reizinot ar to pašu skaitli, kas atšķiras no nulles, daļskaitļu vērtības nemainās.
• Kopumā visas izteiksmes var pārveidot ar darbībām vai ar ķēdi. Pirmā metode ir labāka, jo. starpposma darbību rezultāti ir vieglāk pārbaudāmi.
• Diezgan bieži matemātiskās izteiksmēs ir jāizvelk saknes. Jāatceras, ka pāra grādu saknes var iegūt tikai no nenegatīva skaitļa vai izteiksmes, un nepāra grādu saknes var iegūt pilnībā no jebkādām izteiksmēm vai skaitļiem.

Mēs ceram, ka mūsu raksts palīdzēs jums nākotnē izprast matemātiskās formulas un iemācīs tās pielietot praksē.