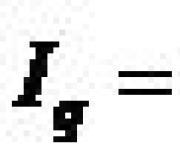Pierādīt ar matemātisko indukciju. Matemātiskās indukcijas metode un tās pielietojums problēmu risināšanā

Ievads

Galvenā daļa

1. Pilnīga un nepilnīga indukcija

2. Matemātiskās indukcijas princips

3. Matemātiskās indukcijas metode

4. Piemēru risinājums

5. Vienādības

6. Skaitļu dalījums

7. Nevienlīdzība

Secinājums

Izmantotās literatūras saraksts

Ievads

Deduktīvās un induktīvās metodes ir jebkura matemātiskā pētījuma pamatā. Deduktīvā spriešanas metode ir spriešana no vispārīgā uz konkrēto, t.i. argumentācija, kuras sākumpunkts ir vispārējais rezultāts, bet beigu punkts ir konkrētais rezultāts. Indukcija tiek izmantota, pārejot no konkrētiem rezultātiem uz vispārīgiem, t.i. ir pretstats deduktīvajai metodei.

Lai gan matemātiskās indukcijas metodes pielietošanas lauks ir audzis, skolas mācību programmā tai tiek veltīts maz laika. Nu saki, ka noderīgu cilvēku atnesīs tās divas vai trīs nodarbības, par kurām viņš dzird piecus teorijas vārdus, atrisina piecas primitīvas problēmas un rezultātā saņem pieci par nezināšanu.

Bet tas ir tik svarīgi – prast domāt induktīvi.

Galvenā daļa

Sākotnējā nozīmē vārds "indukcija" tiek attiecināts uz argumentāciju, ar kuras palīdzību tiek iegūti vispārīgi secinājumi, pamatojoties uz vairākiem konkrētiem apgalvojumiem. Vienkāršākā šāda veida argumentācijas metode ir pilnīga indukcija. Šeit ir šādas argumentācijas piemērs.

Jānosaka, ka katrs naturāls pāra skaitlis n robežās 4< n < 20 представимо в виде суммы двух простых чисел. Для этого возьмём все такие числа и выпишем соответствующие разложения:

4=2+2; 6=3+3; 8=5+3; 10=7+3; 12=7+5;

14=7+7; 16=11+5; 18=13+5; 20=13+7.

Šīs deviņas vienādības parāda, ka katrs no mums interesējošajiem skaitļiem patiešām ir attēlots kā divu galveno terminu summa.

Tādējādi pilnīga indukcija ir tāda, ka vispārīgais apgalvojums tiek pierādīts atsevišķi katrā no ierobežota skaita iespējamo gadījumu.

Dažkārt vispārējo rezultātu var paredzēt, ņemot vērā nevis visus, bet gan lielu skaitu īpašo gadījumu (tā sauktā nepilnīgā indukcija).

Nepilnīgas indukcijas rezultātā iegūtais rezultāts tomēr paliek tikai hipotēze, līdz to pierāda precīza matemātiska argumentācija, aptverot visus īpašos gadījumus. Citiem vārdiem sakot, nepilnīga indukcija matemātikā netiek uzskatīta par likumīgu stingras pierādīšanas metodi, bet tā ir spēcīga metode jaunu patiesību atklāšanai.

Pieņemsim, piemēram, ir jāatrod pirmo n secīgo nepāra skaitļu summa. Apsveriet īpašus gadījumus:

1+3+5+7+9=25=5 2

Apsverot šos dažus īpašos gadījumus, var izdarīt šādu vispārīgu secinājumu:

1+3+5+…+(2n-1)=n 2

tie. pirmo n secīgo nepāra skaitļu summa ir n 2

Protams, veiktais novērojums vēl nevar kalpot par pierādījumu iepriekš minētās formulas pamatotībai.

Pilnīgai indukcijai matemātikā ir tikai ierobežots pielietojums. Daudzi interesanti matemātiski apgalvojumi aptver bezgalīgu skaitu īpašu gadījumu, un mēs nevaram pārbaudīt bezgalīgu skaitu gadījumu. Nepilnīga indukcija bieži noved pie kļūdainiem rezultātiem.

Daudzos gadījumos izeja no šāda veida grūtībām ir ķerties pie īpašas spriešanas metodes, ko sauc par matemātiskās indukcijas metodi. Tas ir šādi.

Pieņemsim, ka jāpierāda noteikta apgalvojuma derīgums jebkuram naturālam skaitlim n (piemēram, jāpierāda, ka pirmo n nepāra skaitļu summa ir vienāda ar n 2). Šī apgalvojuma tieša pārbaude katrai n vērtībai nav iespējama, jo naturālo skaitļu kopa ir bezgalīga. Lai pierādītu šo apgalvojumu, vispirms pārbaudiet tā derīgumu n=1. Tad tiek pierādīts, ka jebkurai k naturālajai vērtībai apskatāmā apgalvojuma derīgums n=k nozīmē tā derīgumu arī n=k+1.

Tad apgalvojums tiek uzskatīts par pierādītu visiem n. Patiešām, apgalvojums ir patiess n=1. Bet tad tas ir spēkā arī nākamajam skaitlim n=1+1=2. Apgalvojuma derīgums n=2 nozīmē tā derīgumu n=2+

1=3. Tas nozīmē apgalvojuma derīgumu n=4 un tā tālāk. Ir skaidrs, ka galu galā mēs sasniegsim jebkuru naturālu skaitli n. Tādējādi apgalvojums ir patiess jebkuram n.

Apkopojot teikto, mēs formulējam šādu vispārīgu principu.

Matemātiskās indukcijas princips.

Ja teikums A(n) atkarībā no naturālā skaitļan, taisnība parn=1 un no tā, ka tā ir patiesan=k(Kurk-jebkurš naturāls skaitlis), no tā izriet, ka tas attiecas arī uz nākamo skaitlin=k+1, tad pieņēmums A(n) attiecas uz jebkuru naturālu skaitlin.

Vairākos gadījumos var būt nepieciešams pierādīt noteikta apgalvojuma derīgumu nevis visiem naturālajiem skaitļiem, bet tikai n>p, kur p ir fiksēts naturāls skaitlis. Šajā gadījumā matemātiskās indukcijas princips ir formulēts šādi. Ja teikums A(n) attiecas uzn=pun ja A(k) Þ A(k+1)jebkuramk>p,tad teikums A(n)taisnība jebkuramn> lpp.

Pierādīšana ar matemātiskās indukcijas metodi tiek veikta šādi. Pirmkārt, tiek pārbaudīts pierādāmais apgalvojums, ja n=1, t.i., tiek konstatēts apgalvojuma A(1) patiesums. Šo pierādījumu daļu sauc par indukcijas bāzi. Tam seko pierādījuma daļa, ko sauc par indukcijas soli. Šajā daļā apgalvojuma derīgums n=k+1 ir pierādīts, pieņemot, ka apgalvojums ir patiess pie n=k (induktīvais pieņēmums), t.i. pierādīt, ka A(k)ÞA(k+1).

1. PIEMĒRS

Pierādīt, ka 1+3+5+…+(2n-1)=n 2 .

Risinājums: 1) Mums ir n=1=1 2 . Tāpēc

apgalvojums ir patiess n=1, t.i. A(1) ir taisnība.

2) Pierādīsim, ka A(k)ÞA(k+1).

Lai k ir jebkurš naturāls skaitlis un apgalvojums ir patiess, ja n=k, t.i.

1+3+5+…+(2k-1)=k 2 .

Pierādīsim, ka tad apgalvojums ir patiess arī nākamajam naturālajam skaitlim n=k+1, t.i. Kas

1+3+5+…+(2k+1)=(k+1) 2 .

Patiešām,

1+3+5+…+(2k-1)+(2k+1)=k 2 +2k+1=(k+1) 2 .

Tātad A(k)ÞA(k+1). Pamatojoties uz matemātiskās indukcijas principu, mēs secinām, ka pieņēmums A(n) ir patiess jebkuram nОN.

2. PIEMĒRS

Pierādiet to

1+x+x 2 +x 3 +…+x n =(x n+1 -1)/(x-1), kur x¹1

Risinājums: 1) Ja n=1 mēs iegūstam

1+x=(x2-1)/(x-1)=(x-1)(x+1)/(x-1)=x+1

tāpēc n=1 formula ir patiesa; A(1) ir taisnība.

2) Lai k ir jebkurš naturāls skaitlis un lai formula būtu patiesa, ja n=k, t.i.

1 + x + x 2 + x 3 + ... + x k \u003d (x k + 1 -1) / (x-1).

Pierādīsim, ka tad vienlīdzība

1+x+x 2 +x 3 +…+x k +x k+1 =(x k+2 -1)/(x-1).

Patiešām

1+х+х 2 +x 3 +…+х k +x k+1 =(1+x+x 2 +x 3 +…+x k)+x k+1 =

=(x k+1 -1)/(x-1)+x k+1 =(x k+2 -1)/(x-1).

Tātad A(k)ÞA(k+1). Pamatojoties uz matemātiskās indukcijas principu, mēs secinām, ka formula ir patiesa jebkuram naturālam skaitlim n.

3. PIEMĒRS

Pierādīt, ka izliekta n-stūra diagonāļu skaits ir n(n-3)/2.

Risinājums: 1) Ja n=3, apgalvojums ir patiess

Un 3 ir pareizi, jo trijstūrī

 A 3 =3(3-3)/2=0 diagonāles;

2 A(3) ir patiess.

2) Pieņemsim, ka jebkurā

izliekts k-gon ir-

A 1 sya A k \u003d k (k-3) / 2 diagonāles.

A k Pierādīsim, ka tad izliektā veidā

(k+1)-gon skaitlis

diagonāles A k+1 =(k+1)(k-2)/2.

Pieņemsim А 1 А 2 А 3 …A k A k+1 -izliekts (k+1)-leņķis. Iezīmēsim tajā diagonāli A 1 A k. Lai saskaitītu kopējo šī (k + 1)-stūra diagonāļu skaitu, jāsaskaita diagonāļu skaits k-gonā A 1 A 2 ...A k , iegūtajam skaitlim jāpievieno k-2, t.i. (k+1)-stūra diagonāļu skaits, kas izplūst no virsotnes A k+1 , un papildus jāņem vērā diagonāle A 1 A k.

Tādējādi

 k+1 = k +(k-2)+1=k(k-3)/2+k-1=(k+1)(k-2)/2.

Tātad A(k)ÞA(k+1). Matemātiskās indukcijas principa dēļ apgalvojums ir patiess jebkuram izliektam n-stūrim.

4. PIEMĒRS

Pierādiet, ka jebkuram n apgalvojums ir patiess:

1 2 +2 2 +3 2 +…+n 2 =n(n+1)(2n+1)/6.

Risinājums: 1) Lai n=1, tad

X 1 \u003d 1 2 = 1 (1 + 1) (2 + 1) / 6 = 1.

Tādējādi n=1 apgalvojums ir patiess.

2) Pieņemsim, ka n=k

X k \u003d k 2 \u003d k (k + 1) (2k + 1) / 6.

3) Apsveriet šo apgalvojumu n=k+1

Xk+1 =(k+1)(k+2)(2k+3)/6.

X k+1 =1 2 +2 2 +3 2 +…+k 2 +(k+1) 2 = k(k+1)(2k+1)/6+ +(k+1) 2 =(k (k+1)(2k+1)+6(k+1) 2)/6=(k+1)(k(2k+1)+

6(k+1))/6=(k+1)(2k2 +7k+6)/6=(k+1)(2(k+3/2)(k+)

2))/6=(k+1)(k+2)(2k+3)/6.

Mēs esam pierādījuši vienādības derīgumu n=k+1, tāpēc, izmantojot matemātiskās indukcijas metodi, apgalvojums ir patiess jebkuram naturālam n.

5. PIEMĒRS

Pierādiet, ka jebkurai dabiskajai n vienādība ir patiesa:

1 3 +2 3 +3 3 +…+n 3 =n 2 (n+1) 2 /4.

Risinājums: 1) n=1.

Tad X 1 = 1 3 = 1 2 (1+1) 2 /4 = 1.

Mēs redzam, ka n=1 apgalvojums ir patiess.

2) Pieņemsim, ka vienādība ir patiesa n=k

Matemātiskās indukcijas metode

Ievads

Galvenā daļa

Pilnīga un nepilnīga indukcija
Matemātiskās indukcijas princips
Matemātiskās indukcijas metode
Piemēru risinājums
Vienlīdzība
Skaitļu dalījums
nevienlīdzības

Secinājums

Izmantotās literatūras saraksts

Ievads

Bet tas ir tik svarīgi – prast domāt induktīvi.

Galvenā daļa

4=2+2; 6=3+3; 8=5+3; 10=7+3; 12=7+5;

14=7+7; 16=11+5; 18=13+5; 20=13+7.

Šīs deviņas vienādības parāda, ka katrs no mums interesējošajiem skaitļiem patiešām ir attēlots kā divu galveno terminu summa.

Tādējādi pilnīga indukcija ir tāda, ka vispārīgais apgalvojums tiek pierādīts atsevišķi katrā no ierobežota skaita iespējamo gadījumu.

Dažkārt vispārējo rezultātu var paredzēt, ņemot vērā nevis visus, bet gan lielu skaitu īpašo gadījumu (tā sauktā nepilnīgā indukcija).

Pieņemsim, piemēram, ir jāatrod pirmo n secīgo nepāra skaitļu summa. Apsveriet īpašus gadījumus:

1+3+5+7+9=25=5 2

Apsverot šos dažus īpašos gadījumus, var izdarīt šādu vispārīgu secinājumu:

1+3+5+…+(2n-1)=n 2

tie. pirmo n secīgo nepāra skaitļu summa ir n 2

Protams, veiktais novērojums vēl nevar kalpot par pierādījumu iepriekš minētās formulas pamatotībai.

Daudzos gadījumos izeja no šāda veida grūtībām ir ķerties pie īpašas spriešanas metodes, ko sauc par matemātiskās indukcijas metodi. Tas ir šādi.

1=3. Tas nozīmē apgalvojuma derīgumu n=4 un tā tālāk. Ir skaidrs, ka galu galā mēs sasniegsim jebkuru naturālu skaitli n. Tādējādi apgalvojums ir patiess jebkuram n.

Apkopojot teikto, mēs formulējam šādu vispārīgu principu.

Matemātiskās indukcijas princips.

Ja teikums A(n), kas ir atkarīgs no naturāla skaitļa n, ir patiess n=1, un no tā, ka tas ir patiess n=k (kur k ir jebkurš naturāls skaitlis), tad tas ir arī patiess nākamajam skaitlim n=k +1, tad pieņēmums A(n) ir patiess jebkuram naturālam skaitlim n.

Ja priekšlikums A(n) ir patiess pie n=p un ja A(k)ÞA(k+1) jebkuram k>p, tad priekšlikums A(n) ir patiess jebkuram n>p.

Pierādīt, ka 1+3+5+…+(2n-1)=n 2 .

Risinājums: 1) Mums ir n=1=1 2 . Tāpēc

apgalvojums ir patiess n=1, t.i. A(1) ir taisnība.

2) Pierādīsim, ka A(k)ÞA(k+1).

Lai k ir jebkurš naturāls skaitlis un apgalvojums ir patiess, ja n=k, t.i.

1+3+5+…+(2k-1)=k 2 .

Pierādīsim, ka tad apgalvojums ir patiess arī nākamajam naturālajam skaitlim n=k+1, t.i. Kas

1+3+5+…+(2k+1)=(k+1) 2 .

Patiešām,

1+3+5+…+(2k-1)+(2k+1)=k 2 +2k+1=(k+1) 2 .

Tātad A(k)ÞA(k+1). Pamatojoties uz matemātiskās indukcijas principu, mēs secinām, ka pieņēmums A(n) ir patiess jebkuram nОN.

Pierādiet to

1+x+x 2 +x 3 +…+x n =(x n+1 -1)/(x-1), kur x¹1

Risinājums: 1) Ja n=1 mēs iegūstam

1+x=(x2-1)/(x-1)=(x-1)(x+1)/(x-1)=x+1

tāpēc n=1 formula ir patiesa; A(1) ir taisnība.

2) Lai k ir jebkurš naturāls skaitlis un lai formula būtu patiesa, ja n=k, t.i.

1 + x + x 2 + x 3 + ... + x k \u003d (x k + 1 -1) / (x-1).

Pierādīsim, ka tad vienlīdzība

1+x+x 2 +x 3 +…+x k +x k+1 =(x k+2 -1)/(x-1).

Patiešām

1+х+х 2 +x 3 +…+х k +x k+1 =(1+x+x 2 +x 3 +…+x k)+x k+1 =

=(x k+1 -1)/(x-1)+x k+1 =(x k+2 -1)/(x-1).

Tātad A(k)ÞA(k+1). Pamatojoties uz matemātiskās indukcijas principu, mēs secinām, ka formula ir patiesa jebkuram naturālam skaitlim n.

Pierādīt, ka izliekta n-stūra diagonāļu skaits ir n(n-3)/2.

Risinājums: 1) Ja n=3, apgalvojums ir patiess

Un 3 ir pareizi, jo trijstūrī

 A 3 =3(3-3)/2=0 diagonāles;

2 A(3) ir patiess.

2) Pieņemsim, ka jebkurā

izliekts k-gon ir-

A 1 sya A k \u003d k (k-3) / 2 diagonāles.

A k Pierādīsim, ka tad izliektā veidā

(k+1)-gon skaitlis

diagonāles A k+1 =(k+1)(k-2)/2.

Tādējādi

 k+1 = k +(k-2)+1=k(k-3)/2+k-1=(k+1)(k-2)/2.

Tātad A(k)ÞA(k+1). Matemātiskās indukcijas principa dēļ apgalvojums ir patiess jebkuram izliektam n-stūrim.

Pierādiet, ka jebkuram n apgalvojums ir patiess:

1 2 +2 2 +3 2 +…+n 2 =n(n+1)(2n+1)/6.

Risinājums: 1) Lai n=1, tad

X 1 \u003d 1 2 = 1 (1 + 1) (2 + 1) / 6 = 1.

Tādējādi n=1 apgalvojums ir patiess.

2) Pieņemsim, ka n=k

X k \u003d k 2 \u003d k (k + 1) (2k + 1) / 6.

3) Apsveriet šo apgalvojumu n=k+1

Xk+1 =(k+1)(k+2)(2k+3)/6.

X k+1 =1 2 +2 2 +3 2 +…+k 2 +(k+1) 2 = k(k+1)(2k+1)/6+ +(k+1) 2 =(k (k+1)(2k+1)+6(k+1) 2)/6=(k+1)(k(2k+1)+

6(k+1))/6=(k+1)(2k2 +7k+6)/6=(k+1)(2(k+3/2)(k+)

2))/6=(k+1)(k+2)(2k+3)/6.

Mēs esam pierādījuši vienādības derīgumu n=k+1, tāpēc, izmantojot matemātiskās indukcijas metodi, apgalvojums ir patiess jebkuram naturālam n.

Pierādiet, ka jebkurai dabiskajai n vienādība ir patiesa:

1 3 +2 3 +3 3 +…+n 3 =n 2 (n+1) 2 /4.

Risinājums: 1) n=1.

Tad X 1 = 1 3 = 1 2 (1+1) 2 /4 = 1.

Mēs redzam, ka n=1 apgalvojums ir patiess.

2) Pieņemsim, ka vienādība ir patiesa n=k

X k \u003d k 2 (k + 1) 2/4.

3) Pierādīsim šī apgalvojuma patiesumu n=k+1, t.i.

X k+1 =(k+1) 2 (k+2) 2 /4. X k+1 =1 3 +2 3 +…+k 3 +(k+1) 3 =k 2 (k+1) 2 /4+(k+1) 3 = (k 2 (k++1) 2 +4(k+1) 3)/4=(k+1) 2 (k 2 +4k+4)/4=(k+1) 2 (k+2) 2 /4.

No iepriekšminētā pierādījuma ir skaidrs, ka apgalvojums ir patiess n=k+1, tāpēc vienādība ir patiesa jebkuram naturālam n.

Pierādiet to

((2 3 +1)/(2 3 -1))´((3 3 +1)/(3 3 -1))´…´((n 3 +1)/(n 3 -1))= 3n(n+1)/2(n2+n+1), kur n>2.

Risinājums: 1) n=2 identitāte izskatās šādi: (2 3 +1)/(2 3 -1)=(3´2´3)/2(2 2 +2+1),

tie. tas ir pareizi.

2) Pieņemsim, ka izteiksme ir patiesa n=k

(2 3 +1)/(2 3 -1)´…´(k 3 +1)/(k 3 -1)=3k(k+1)/2(k2+k+1).

3) Pierādīsim izteiksmes pareizību n=k+1.

(((2 3 +1)/(2 3 -1))´…´((k 3 +1)/(k 3 -1)))´(((k+1) 3 +

1)/((k+1) 3 -1))=(3k(k+1)/2(k2 +k+1))´((k+2)((k+)

1) 2-(k+1)+1)/k((k+1) 2 +(k+1)+1))=3(k+1)(k+2)/2´

´((k+1) 2 +(k+1)+1).

Mēs esam pierādījuši vienādības derīgumu n=k+1, tāpēc matemātiskās indukcijas metodes dēļ apgalvojums ir patiess jebkuram n>2

Pierādiet to

1 3-2 3 +3 3 -4 3 +…+(2n-1) 3-(2n) 3 =-n 2 (4n+3)

jebkurai dabiskai n.

Risinājums: 1) Lai n=1, tad

1 3 -2 3 =-1 3 (4+3); -7=-7.

2) Pieņemsim, ka n=k, tad

1 3 -2 3 +3 3 -4 3 +…+(2k-1) 3-(2k) 3 =-k 2 (4k+3).

3) Pierādīsim šī apgalvojuma patiesumu n=k+1

(1 3 k+2 3 +…+(2 k-1) 3 (2 k) 3)+(2 k+1) 3 (2 k+2) 3 = k 2 (4 k+3)+

+(2k+1)3-(2k+2)3 =-(k+1)3 (4(k+1)+3).

Ir pierādīts arī vienādības derīgums n=k+1, tāpēc apgalvojums ir patiess jebkuram naturālam skaitlim n.

Pierādiet identitātes derīgumu

(1 2 /1´3)+(2 2/3´5)+…+(n 2 /(2n-1)´(2n+1))=n(n+1)/2(2n+1)

jebkurai dabiskai n.

1) Ja n=1, identitāte ir patiesa 1 2 /1´3=1(1+1)/2(2+1).

2) Pieņemsim, ka n=k

(1 2 /1'3)+…+(k 2 /(2k-1)´(2k+1))=k(k+1)/2(2k+1).

3) Pierādīsim, ka identitāte ir patiesa n=k+1.

(1 2 /1´3)+…+(k 2 /(2k-1)(2k+1))+(k+1) 2 /(2k+1)(2k+3)=(k(k+ 1) )/2(2k+1))+((k+1) 2 /(2k+1)(2k+3))=((k+1)/(2k+1))´((k/2) +((k+1)/(2k+3)))=(k+1)(k+2)´ (2k+1)/2(2k+1)(2k+3)=(k+1) (k+2)/2(2(k+1)+1).

No iepriekš minētā pierādījuma var redzēt, ka apgalvojums ir patiess jebkuram naturālam skaitlim n.

Pierādīt, ka (11 n+2 +12 2n+1) dalās ar 133 bez atlikuma.

Risinājums: 1) Lai n=1, tad

11 3 + 12 3 \u003d (11 + 12) (11 2 -132 + 12 2) \u003d 23´133.

Bet (23´133) dalās ar 133 bez atlikuma, tāpēc n=1 apgalvojums ir patiess; A(1) ir taisnība.

2) Pieņemsim, ka (11 k+2 +12 2k+1) dalās ar 133 bez atlikuma.

3) Pierādīsim to šajā gadījumā

(11 k+3 +12 2k+3) dalās ar 133 bez atlikuma. Patiešām, 11 k+3 +12 2k+3 =11´11 k+2 +12 2´ 12 2k+1 =11´11 k+2 +

+(11+133)´12 2k+1 =11(11 k+2 +12 2k+1)+133´12 2k+1.

Iegūtā summa dalās ar 133 bez atlikuma, jo tās pirmais loceklis ar pieņēmumu dalās ar 133 bez atlikuma, bet otrajā viens no faktoriem ir 133. Tātad А(k)ÞА(k+1). Izmantojot matemātiskās indukcijas metodi, apgalvojums ir pierādīts.

Pierādīt, ka jebkuram n 7 n -1 dalās ar 6 bez atlikuma.

Risinājums: 1) Lai n=1, tad X 1 =7 1 -1=6 tiek dalīts ar 6 bez atlikuma. Tātad n=1 apgalvojums ir patiess.

2) Pieņemsim, ka n=k

7 k -1 dalās ar 6 bez atlikuma.

3) Pierādīsim, ka apgalvojums ir patiess n=k+1.

X k+1 =7 k+1 -1=7´7 k -7+6=7(7 k -1)+6.

Pirmais loceklis dalās ar 6, jo 7 k -1 dalās ar 6 pēc pieņēmuma, bet otrais loceklis ir 6. Tātad 7 n -1 ir skaitļa 6 reizinājums jebkuram naturālam n. Izmantojot matemātiskās indukcijas metodi, apgalvojums ir pierādīts.

Pierādīt, ka 3 3n-1 +2 4n-3 patvaļīgai naturālai n dalās ar 11.
Risinājums: 1) Lai n=1, tad

X 1 \u003d 3 3-1 +2 4-3 \u003d 3 2 +2 1 \u003d 11 tiek dalīts ar 11 bez atlikuma. Tādējādi n=1 apgalvojums ir patiess.

2) Pieņemsim, ka n=k

X k \u003d 3 3k-1 +2 4k-3 dalās ar 11 bez atlikuma.

3) Pierādīsim, ka apgalvojums ir patiess n=k+1.

X k+1 =3 3(k+1)-1 +2 4(k+1)-3 =3 3k+2 +2 4k+1 =3 3´ 3 3k-1 +2 4´ 2 4k-3 =

27´3 3k-1 +16´2 4k-3 =(16+11)´3 3k-1 +16´2 4k-3 =16´3 3k-1 +

11´3 3k-1 +16´2 4k-3 =16(3 3k-1 +2 4k-3)+11´3 3k-1.

Pirmais loceklis dalās ar 11 bez atlikuma, jo 3 3k-1 +2 4k-3 dalās ar 11 pēc pieņēmuma, otrais dalās ar 11, jo viens no tā faktoriem ir skaitlis 11. Tātad summa ir arī dalās ar 11 bez atlikuma jebkuram naturālam n. Izmantojot matemātiskās indukcijas metodi, apgalvojums ir pierādīts.

Pierādīt, ka 11 2n -1 patvaļīgam pozitīvam veselam skaitlim n dalās ar 6 bez atlikuma.

Risinājums: 1) Lai n=1, tad 11 2 -1=120 dalās ar 6 bez atlikuma. Tātad n=1 apgalvojums ir patiess.

2) Pieņemsim, ka n=k

11 2k -1 dalās ar 6 bez atlikuma.

11 2(k+1) -1=121´11 2k -1=120´11 2k +(11 2k -1).

Abi termini dalās ar 6 bez atlikuma: pirmais satur skaitļa 120 daudzkārtni, bet otrais dalās ar 6 bez atlikuma, pieņemot pieņēmumu. Tātad summa dalās ar 6 bez atlikuma. Izmantojot matemātiskās indukcijas metodi, apgalvojums ir pierādīts.

Pierādīt, ka 3 3n+3 -26n-27 patvaļīgam pozitīvam veselam skaitlim n dalās ar 26 2 (676) bez atlikuma.

Risinājums: Vispirms pierādīsim, ka 3 3n+3 -1 dalās ar 26 bez atlikuma.

Ja n=0

3 3 -1=26 dalās ar 26

Pieņemsim, ka n=k

3 3k+3 -1 dalās ar 26

Pierādīsim šo apgalvojumu

patiess n=k+1.

3 3k+6 -1=27´3 3k+3 -1=26´3 3k+3 +(3 3k+3 -1) – dalās ar 26

Tagad pierādīsim apgalvojumu, kas formulēts problēmas nosacījumā.

1) Ir skaidrs, ka n=1 apgalvojums ir patiess

3 3+3 -26-27=676

2) Pieņemsim, ka n=k

izteiksme 3 3k+3 -26k-27 dalās ar 26 2 bez atlikuma.

3) Pierādīsim, ka apgalvojums ir patiess n=k+1

3 3k+6 -26(k+1)-27=26(3 3k+3 -1)+(3 3k+3 -26k-27).

Abi termini dalās ar 26 2 ; pirmā dalās ar 26 2, jo esam pierādījuši, ka izteiksme iekavās dalās ar 26, bet otrā – ar induktīvo hipotēzi. Izmantojot matemātiskās indukcijas metodi, apgalvojums ir pierādīts.

Pierādīt, ja n>2 un x>0, tad nevienādība

(1+x) n >1+n´x.

Risinājums: 1) Ja n=2, nevienādība ir patiesa, jo

(1+x) 2 =1+2x+x 2 >1+2x.

Tātad A(2) ir taisnība.

2) Pierādīsim, ka A(k)ÞA(k+1), ja k> 2. Pieņemsim, ka A(k) ir patiess, t.i., ka nevienādība

(1+x) k > 1+k´x. (3)

Pierādīsim, ka tad arī A(k+1) ir patiess, t.i., ka nevienādība

(1+x) k+1 >1+(k+1)´x.

Patiešām, reizinot abas nevienādības (3) puses ar pozitīvu skaitli 1+x, mēs iegūstam

(1+x) k+1 >(1+k´x)(1+x).

Apsveriet pēdējo nevienlīdzīgo labo pusi

stva; mums ir

(1+k´x)(1+x)=1+(k+1)´x+k´x 2 >1+(k+1)´x.

Rezultātā mēs to iegūstam

(1+x) k+1 >1+(k+1)´x.

Tātad A(k)ÞA(k+1). Pamatojoties uz matemātiskās indukcijas principu, var apgalvot, ka Bernulli nevienādība ir spēkā jebkurai

Pierādiet, ka nevienlīdzība ir patiesa

(1+a+a 2) m > 1+m´a+(m(m+1)/2)´a 2, ja a> 0.

Risinājums: 1) Ja m=1

(1+a+a 2) 1 > 1+a+(2/2)´a 2 abas daļas ir vienādas.

2) Pieņemsim, ka m=k

(1+a+a 2) k >1+k´a+(k(k+1)/2)´a 2

3) Pierādīsim, ka m=k+1 nevienādība ir patiesa

(1+a+a 2) k+1 =(1+a+a 2)(1+a+a 2) k >(1+a+a 2)(1+k´a+

+(k(k+1)/2)´a 2)=1+(k+1)´a+((k(k+1)/2)+k+1)´a 2 +

+((k(k+1)/2)+k)´a 3 +(k(k+1)/2)´a 4 > 1+(k+1)´a+

+((k+1)(k+2)/2)´a 2 .

Mēs esam pierādījuši nevienādības derīgumu m=k+1, tāpēc, izmantojot matemātiskās indukcijas metodi, nevienādība ir patiesa jebkuram naturālam m.

Pierādiet, ka n>6 nevienādība

3 n >n´2 n+1 .

Risinājums: Pārrakstīsim nevienādību formā

Par n=7 mums ir

37/27 =2187/128>14=2´7

nevienlīdzība ir patiesa.

Pieņemsim, ka n=k

3) Pierādīsim nevienādības pareizību n=k+1.

3k+1 /2k+1 =(3k /2k)´(3/2)>2k´(3/2)=3k>2(k+1).

Tā kā k>7, pēdējā nevienādība ir acīmredzama.

Pamatojoties uz matemātiskās indukcijas metodi, nevienlīdzība ir spēkā jebkurai dabiskajai n.

Pierādiet, ka n>2 nevienādība

1+(1/2 2)+(1/3 2)+…+(1/n 2)<1,7-(1/n).

Risinājums: 1) n=3 nevienādība ir patiesa

1+(1/2 2)+(1/3 2)=245/180<246/180=1,7-(1/3).

Pieņemsim, ka n=k

1+(1/2 2)+(1/3 2)+…+(1/k 2)=1,7-(1/k).

3) mēs pierādīsim neesības derīgumu

vienādības n=k+1

(1+(1/2 2)+…+(1/k 2))+(1/(k+1) 2)<1,7-(1/k)+(1/(k+1) 2).

Pierādīsim, ka 1,7-(1/k)+(1/(k+1) 2)<1,7-(1/k+1)Û

w(1/(k+1) 2)+(1/k+1)<1/kÛ(k+2)/(k+1) 2 <1/kÛ

Ûk(k+2)<(k+1) 2Û k 2 +2k

Pēdējais ir acīmredzams, un tāpēc

1+(1/2 2)+(1/3 2)+…+(1/(k+1) 2)<1,7-(1/k+1).

Izmantojot matemātiskās indukcijas metodi, tiek pierādīta nevienlīdzība.

Secinājums

Jo īpaši, izpētījis matemātiskās indukcijas metodi, es uzlaboju savas zināšanas šajā matemātikas jomā, kā arī uzzināju, kā atrisināt problēmas, kuras iepriekš nebija manā spēkos.

Būtībā tie bija loģiski un izklaidējoši uzdevumi, t.i. tikai tie, kas palielina interesi par pašu matemātiku kā zinātni. Šādu uzdevumu risināšana kļūst par izklaidējošu nodarbi un var piesaistīt matemātikas labirintos arvien vairāk zinātkāru. Manuprāt, tas ir jebkuras zinātnes pamatā.

Turpinot pētīt matemātiskās indukcijas metodi, mēģināšu iemācīties to pielietot ne tikai matemātikā, bet arī fizikas, ķīmijas un pašas dzīves uzdevumu risināšanā.

MATEMĀTIKA:

LEKCIJAS, UZDEVUMI, RISINĀJUMI

Mācību grāmata / V. G. Boltjanskis, Ju. V. Sidorovs, M. I. Šabuņins. Potpourri LLC 1996.

ALGEBRA UN ANALĪZES PRINCIPI

Mācību grāmata / I.T.Demidovs, A.N.Kolmogorovs, S.I.Švartsburga, O.S.Ivaševs-Musatovs, B.E.Veits. "Apgaismība" 1975.

Viena no svarīgākajām matemātiskās pierādīšanas metodēm ir pareizi matemātiskās indukcijas metode. Lielāko daļu formulu, kas attiecas uz visiem naturālajiem skaitļiem n, var pierādīt ar matemātisko indukciju (piemēram, aritmētiskās progresijas pirmo n vārdu summas formula, Ņūtona binominālā formula utt.).

Šajā rakstā mēs vispirms pakavēsimies pie pamatjēdzieniem, pēc tam aplūkosim pašu matemātiskās indukcijas metodi un analizēsim tās pielietojuma piemērus vienlīdzību un nevienlīdzību pierādīšanā.

Lapas navigācija.

Indukcija un dedukcija.

ar indukcijas palīdzību sauc par pāreju no īpašiem uz vispārīgiem apgalvojumiem. Gluži pretēji, tiek saukta pāreja no vispārīgiem apgalvojumiem uz konkrētiem atskaitīšana.

Privāta paziņojuma piemērs: 254 dalās ar 2 bez atlikuma.

No šī konkrētā apgalvojuma var formulēt daudz vispārīgāku apgalvojumu, gan patiesu, gan nepatiesu. Piemēram, vispārīgāks apgalvojums, ka visi veseli skaitļi, kas beidzas ar 4, dalās ar 2 bez atlikuma, ir patiess, savukārt apgalvojums, ka visi trīsciparu skaitļi dalās ar 2 bez atlikuma, ir nepatiess.

Tādējādi indukcija ļauj iegūt daudzus vispārīgus apgalvojumus, kuru pamatā ir zināmi vai acīmredzami fakti. Un matemātiskās indukcijas metode ir paredzēta, lai noteiktu saņemto apgalvojumu pamatotību.

Kā piemēru apsveriet ciparu secību: , n ir patvaļīgs naturāls skaitlis. Tad šīs secības pirmo n elementu summu secība būs šāda

Pamatojoties uz šo faktu, ar indukcijas palīdzību var apgalvot, ka .

Mēs piedāvājam šīs formulas pierādījumu.

Matemātiskās indukcijas metode.

Matemātiskās indukcijas metode ir balstīta uz matemātiskās indukcijas princips.

Tas sastāv no sekojošā: noteikts apgalvojums ir patiess jebkuram naturālam n ja

tas ir derīgs n = 1 un
no apgalvojuma derīguma jebkurai patvaļīgai naturālai n = k izriet, ka tas ir patiess n = k+1 .

Tas ir, pierādīšana ar matemātiskās indukcijas metodi tiek veikta trīs posmos:

pirmkārt, apgalvojuma derīgumu pārbauda jebkuram naturālam skaitlim n (parasti pārbaudi veic n = 1 );
otrkārt, apgalvojuma derīgums tiek pieņemts jebkuram naturālam n=k ;
treškārt, tiek pierādīta apgalvojuma derīgums skaitlim n=k+1, sākot no otrā punkta pieņēmuma.

Vienādojumu un nevienādību pierādījumu piemēri ar matemātiskās indukcijas metodi.

Atgriezīsimies pie iepriekšējā piemēra un pierādīsim formulu .

Pierādījums.

Matemātiskās indukcijas metode ietver trīs punktu pierādījumu.

Tādējādi visi trīs matemātiskās indukcijas metodes soļi ir pabeigti, un līdz ar to ir pierādīts mūsu pieņēmums par formulu.

Apskatīsim trigonometrisko uzdevumu.

Piemērs.

Pierādīt identitāti .

Risinājums.

Pirmkārt, mēs pārbaudām vienādību n = 1. Lai to izdarītu, mums ir vajadzīgas trigonometrijas pamatformulas.

Tas nozīmē, ka vienādība ir patiesa n = 1 .

Otrkārt, pieņemsim, ka vienādība ir patiesa n = k , tas ir, identitātei

Treškārt, mēs pievēršamies vienlīdzības pierādījumam ja n = k+1 , pamatojoties uz otro punktu.

Tā kā pēc formulas no trigonometrijas

Tas

Vienlīdzības pierādījums no trešā punkta ir pabeigts, tāpēc sākotnējā identitāte tiek pierādīta ar matemātiskās indukcijas metodi.

Var pierādīt ar matemātisko indukciju.

Piemērs nevienādības pierādīšanai ar matemātisko indukciju ir atrodams sadaļā par mazāko kvadrātu metodi, atvasinot formulas aproksimācijas koeficientu atrašanai.

Bibliogrāfija.

Sominskis I.S., Golovina L.I., Jagloms I.M. Par matemātisko indukciju.

Saratovas apgabala Izglītības ministrija

Saratovas Valsts sociāli ekonomiskā universitāte

Reģionālais skolēnu matemātikas un datordarbu konkurss

"Nākotnes vektors — 2007"

«Matemātiskās indukcijas metode.

Tās pielietojums algebrisko problēmu risināšanā"

(sadaļa "matemātika")

radošs darbs

10"A" klases skolēni

SM "Ģimnāzija Nr.1"

Saratovas Oktjabrskas rajons

Harutjunjans Gajana.

Darba vadītājs:

matemātikas skolotājs

Grišina Irina Vladimirovna

Saratova

2007

Ievads…………………………………………………………………………………3

Matemātiskās indukcijas princips un tā

pierādījums ……………………………………………………………………………..4

Problēmu risināšanas piemēri…………………………………………………………………..9

Secinājums………………………………………………………………………………..16

Literatūra……………………………………………………………………………………17

Ievads.

Matemātiskās indukcijas metodi var salīdzināt ar progresu. Mēs sākam no zemākā, loģiskās domāšanas rezultātā nonākam līdz augstākajam. Cilvēks vienmēr ir tiecies pēc progresa, pēc spējas loģiski attīstīt savu domu, kas nozīmē, ka pati daba viņam ir lēmusi domāt induktīvi un nostiprināt savu domu ar pierādījumiem, kas veikti saskaņā ar visiem loģikas likumiem.
Šobrīd matemātiskās indukcijas metodes pielietošanas lauks ir audzis, bet diemžēl skolas mācību programmā tai tiek veltīts maz laika. Bet tas ir tik svarīgi – prast domāt induktīvi.

Matemātiskās indukcijas princips un tā pierādījums

Pievērsīsimies matemātiskās indukcijas metodes būtībai. Apskatīsim dažādus apgalvojumus. Tos var iedalīt vispārīgajos un specifiskajos. Sniegsim vispārīgu apgalvojumu piemērus.

Visiem Krievijas pilsoņiem ir tiesības uz izglītību.

Jebkurā paralelogramā diagonāles krustošanās punktā ir sadalītas uz pusēm.

Visi skaitļi, kas beidzas ar nulli, dalās ar 5.

Atbilstoši privātu paziņojumu piemēri:

Petrovam ir tiesības uz izglītību.

Paralelogrammā ABCD diagonāles krustojuma punktā ir sadalītas uz pusēm.

140 dalās ar 5.

Pāreju no vispārīgiem apgalvojumiem uz konkrētiem sauc par dedukciju (no latīņu valodas atskaitījums - secinājums saskaņā ar loģikas noteikumiem).

Apsveriet deduktīvās secinājuma piemēru.

Visiem Krievijas pilsoņiem ir tiesības uz izglītību. (1)

Petrovs ir Krievijas pilsonis. (2)

Petrovam ir tiesības uz izglītību. (3)

No vispārējā apgalvojuma (1) ar (2) palīdzību tiek iegūts konkrētais apgalvojums (3).

Apgriezto pāreju no konkrētiem apgalvojumiem uz vispārīgiem apgalvojumiem sauc par indukciju (no latīņu valodas indukcija - norādījumi).

Indukcija var radīt gan pareizus, gan nepareizus secinājumus.

Paskaidrosim to ar diviem piemēriem.

140 dalās ar 5. (1)

Visi skaitļi, kas beidzas ar nulli, dalās ar 5. (2)

140 dalās ar 5. (1)

Visi trīsciparu skaitļi dalās ar 5. (2)

No konkrētā apgalvojuma (1) iegūst vispārīgo apgalvojumu (2). Apgalvojums (2) ir patiess.

Otrais piemērs parāda, kā vispārīgu apgalvojumu (3) var iegūt no konkrēta apgalvojuma (1) , turklāt apgalvojums (3) nav patiess.

Uzdosim sev jautājumu, kā izmantot indukciju matemātikā, lai iegūtu tikai pareizus secinājumus. Apskatīsim dažus indukcijas piemērus, kas matemātikā ir nepieņemami.

1. piemērs.

Apsveriet kvadrātveida trinomu ar šādu formu Р(x)= x 2 + x + 41, kam Leonards Eilers pievērsa uzmanību.

P(0) = 41, P(1) = 43, P(2) = 47, P(3) = 53, P(4) = 61, P(5) = 71, P(6) = 83, P (7) = 97, P(8) = 113, P(9) = 131, P(10) = 151.

Mēs redzam, ka katru reizi trinoma vērtība ir pirmskaitlis. Pamatojoties uz iegūtajiem rezultātiem, mēs apgalvojam, ka, aizstājot aplūkojamo trinomu, nevis x Jebkurš nenegatīvs vesels skaitlis vienmēr rada pirmskaitli.

Tomēr izdarīto secinājumu nevar uzskatīt par ticamu. Kas noticis? Fakts ir tāds, ka argumentācijā vispārīgi apgalvojumi par jebkuru x tiek sniegti tikai tāpēc, ka šis apgalvojums izrādījās patiess dažām x vērtībām.

Patiešām, rūpīgāk izpētot trinomu P(x), skaitļi P(0), P(1), ..., P(39) ir pirmskaitļi, bet P(40) = 41 2 ir salikts skaitlis. Un pavisam skaidri: P(41) = 41 2 +41+41 ir 41 reizinājums.

Šajā piemērā mēs tikāmies ar apgalvojumu, kas ir patiess 40 īpašos gadījumos un tomēr kopumā izrādījās negodīgs.

Apskatīsim vēl dažus piemērus.

2. piemērs

17. gadsimtā V.G. Leibnics pierādīja, ka jebkuram naturālam n skaitļi formā n 3 - n ir skaitļa 3 daudzkārtņi, n 5 - n ir 5 daudzkārtņi, n 7 - n ir 7 daudzkārtņi. Pamatojoties uz to, viņš ierosināja, ka jebkuram nepāra k un naturālais n, skaitlis n k - n k daudzkārtnis, bet drīz viņš pats pamanīja, ka 2 9 -2=510, kas, acīmredzot, nedalās ar 9.

Apskatītie piemēri ļauj izdarīt svarīgu secinājumu: apgalvojums var būt patiess vairākos īpašos gadījumos un tajā pašā laikā netaisnīgs kopumā.

Protams, rodas jautājums: ir apgalvojums, kas ir patiess vairākos atsevišķos gadījumos; nav iespējams izskatīt visus īpašos gadījumus; kā zināt, vai šis apgalvojums vispār ir patiess?

Šo jautājumu dažreiz var atrisināt, izmantojot īpašu spriešanas metodi, ko sauc par matemātiskās indukcijas metodi. Šī metode ir balstīta uz matemātiskās indukcijas princips, secināts šādi: apgalvojums ir patiess jebkuram dabiskajam n, ja:

tas ir derīgs n = 1;

no apgalvojuma derīguma kādam patvaļīgam naturālam n =k , izriet, ka tas ir patiess n = k +1.

Pierādījums.

Pieņemsim pretējo, tas ir, lai apgalvojums būtu patiess ne katram dabiskajam n. Tad ir tāds naturāls skaitlis m, ka

apgalvojums par n = m nav patiess,

visiem n

Ir skaidrs, ka m >1, jo n =1 apgalvojums ir patiess (1. nosacījums). Tāpēc m -1 ir naturāls skaitlis. Naturālam skaitlim m -1 apgalvojums ir patiess, bet nākamajam naturālajam skaitlim m nav patiess. Tas ir pretrunā ar 2. nosacījumu. Iegūtā pretruna parāda, ka pieņēmums ir nepareizs. Tāpēc apgalvojums ir patiess jebkuram dabiskajam n, h.e.d.

Pierādījumu, kas balstīts uz matemātiskās indukcijas principu, sauc par pierādījumu ar matemātiskās indukcijas metodi. Šādam pierādījumam vajadzētu sastāvēt no divām daļām, sākot no divu neatkarīgu teorēmu pierādījuma.

1. teorēma. Apgalvojums ir patiess, ja n =1.

2. teorēma. Apgalvojums ir patiess n =k +1, ja tas ir patiess n=k, kur k ir patvaļīgs naturāls skaitlis.

Ja abas šīs teorēmas ir pierādītas, tad, pamatojoties uz matemātiskās indukcijas principu, apgalvojums ir patiess jebkuram
dabiskais n .

Jāuzsver, ka pierādīšanai ar matemātisko indukciju noteikti ir jāpierāda gan 1., gan 2. teorēma. 2. teorēmas neievērošana noved pie nepareiziem secinājumiem (1.-2. piemēri). Parādīsim ar piemēru, cik nepieciešams ir 1. teorēmas pierādījums.

3. piemērs. "Teorēma": katrs naturālais skaitlis ir vienāds ar naturālo skaitli, kas tam seko.

Pierādīšana tiks veikta ar matemātiskās indukcijas metodi.

Pieņemsim, ka k =k +1 (1).

Pierādīsim, ka k +1=k +2 (2). Lai to izdarītu, katrai "vienlīdzības" daļai pievienojiet 1. Mēs iegūstam "vienlīdzību" (2). Izrādās, ja apgalvojums ir patiess n =k , tad tas ir patiess arī n =k +1. utt.

Acīmredzama "teorēmas" "seka": visi naturālie skaitļi ir vienādi.

Kļūda slēpjas tajā, ka 1. teorēma, kas nepieciešama matemātiskās indukcijas principa piemērošanai, nav pierādīta un nav patiesa, bet ir pierādīta tikai otrā teorēma.

1. un 2. teorēma ir īpaši svarīga.

1. teorēma rada indukcijas pamatu. 2. teorēma dod tiesības uz neierobežotu automātisku šīs bāzes paplašināšanu, tiesības pāriet no šī konkrētā gadījuma uz nākamo, no n uz n + 1.

Ja 1. teorēma nav pierādīta, bet 2. teorēma ir pierādīta, tad līdz ar to indukcijas pamats nav izveidots, un tad nav jēgas piemērot 2. teorēmu, jo patiesībā nav ko paplašināt.

Ja 2. teorēma nav pierādīta, bet ir pierādīta tikai teorēma 1, tad, lai gan ir izveidota bāze indukcijas veikšanai, nav tiesību paplašināt šo bāzi.

Piezīmes.

Dažkārt otrā pierādījuma daļa balstās uz apgalvojuma derīgumu ne tikai n =k, bet arī n =k -1. Šajā gadījumā pirmajā daļā esošais apgalvojums ir jāpārbauda nākamajām divām n vērtībām.

Dažkārt apgalvojums tiek pierādīts nevis jebkuram naturālam n , bet gan n > m , kur m ir kāds vesels skaitlis. Šajā gadījumā pierādījuma pirmajā daļā apgalvojums tiek pārbaudīts n = m +1 un, ja nepieciešams, vairākām turpmākajām n vērtībām.

Apkopojot teikto, mums ir šāds: matemātiskās indukcijas metode ļauj, meklējot vispārīgu likumu, pārbaudīt hipotēzes, kas rodas šajā gadījumā, atmest nepatiesās un apgalvot patiesās.

Ikviens zina, kāda nozīme ir atsevišķu novērojumu un eksperimentu rezultātu vispārināšanas (ti, indukcijas) procesiem empīriskajām, eksperimentālajām zinātnēm. Savukārt matemātika jau sen tiek uzskatīta par klasisku tīri deduktīvu metožu ieviešanas piemēru, jo vienmēr tieši vai netieši tiek pieņemts, ka visi matemātiskie priekšlikumi (izņemot tos, kas pieņemti kā sākotnējie – aksiomas) ir pierādīti un konkrēti pielietojumi. no šiem priekšlikumiem ir atvasināti no pierādījumiem, kas piemēroti vispārīgiem gadījumiem (dukcija).

Ko matemātikā nozīmē indukcija? Vai tā jāsaprot kā ne visai uzticama metode, un kā meklēt šādu induktīvo metožu uzticamības kritēriju? Vai tāda paša rakstura matemātisko secinājumu pārliecība kā eksperimentālo zinātņu eksperimentālie vispārinājumi, lai nebūtu slikti “pārbaudīt” jebkuru pierādītu faktu? Patiesībā tas tā nav.

Hipotēzes indukcijai (vadīšanai) ir ļoti svarīga, bet tīri heiristiska loma matemātikā: tā ļauj uzminēt, kādam vajadzētu būt risinājumam. Bet matemātiskie priekšlikumi tiek noteikti tikai deduktīvi. Un matemātiskās indukcijas metode ir tīri deduktīva pierādīšanas metode. Patiešām, pierādījums, kas veikts ar šo metodi, sastāv no divām daļām:

tā sauktais "bāze" - vēlamā teikuma deduktīvs pierādījums vienam (vai vairākiem) naturāliem skaitļiem;

induktīvs solis, kas sastāv no vispārēja apgalvojuma deduktīva pierādījuma. Teorēma ir precīzi pierādīta visiem naturālajiem skaitļiem. No pierādītā pamata, piemēram, skaitlim 0, mēs ar indukcijas soli iegūstam pierādījumu skaitlim 1, tad tādā pašā veidā 2, 3 ... - un tādējādi apgalvojumu var pamatot jebkurš naturāls skaitlis.

Citiem vārdiem sakot, nosaukums "matemātiskā indukcija" ir saistīts ar to, ka šī metode mūsu prātos vienkārši ir saistīta ar tradicionālo induktīvo spriešanu (galu galā, pamats patiešām ir pierādīts tikai konkrētam gadījumam); induktīvais solis, atšķirībā no induktīvās spriešanas ticamības kritērijiem, pamatojoties uz pieredzi dabas un sociālajās zinātnēs, ir vispārīgs apgalvojums, kam nav vajadzīgs īpašs priekšnoteikums un kas tiek pierādīts saskaņā ar stingriem deduktīvās spriešanas kanoniem. Tāpēc matemātisko indukciju sauc par "pilnīgu" vai "perfektu", jo tā ir deduktīva, pilnīgi uzticama pierādīšanas metode.

Problēmu risinājumu piemēri

Indukcija algebrā

Apsveriet vairākus algebrisko problēmu piemērus, kā arī dažādu nevienādību pierādījumus, kurus var atrisināt, izmantojot matemātiskās indukcijas metodi.

1. uzdevums. Uzminiet summas formulu un pierādiet to.

A( n )= 2  1 2 + 3  2 2 + …..+(n +1) n 2 .

Risinājums.

1. Pārveidosim izteiksmi summai А(n):

A(n)= 2  1 2 + 3  2 2 + ….+ (n+1) n 2 = (1+1) 1 2 + (2+1) 2 2 + …. + (n+1) n 2 = =1  1 2 + 2  2 2 + …+n  n 2 + 1 2 + 2 2 +… +n 2 =1 3 + 2 3 +… +n 3 +1 2 + 2 2 +… +n 2 = В(n) + C(n), kur B(n) = 1 3 + 2 3 + …..+ n 3, C(n) = 1 2 + 2 2 + …+ n 2 .

2. Aplūkosim summas C (n) un B (n).

a) C( n ) = 1 2 + 2 2 +…+ n 2 . Viena no matemātiskās indukcijas metodes bieži sastopamajām problēmām ir pierādīt, ka jebkurai dabiskajai n vienlīdzība

1 2 + 2 2 +…+ n 2 = (1)

Pieņemsim, ka (1) ir patiess visiem n  N.

b ) B(n) = 1 3 + 2 3 + …..+ n 3 . Novērosim, kā mainās B (n) vērtības atkarībā no n.

B(1) = 1 3 = 1 .

B(2) = 1 3 + 2 3 = 9 = 3 2 = (1 + 2) 2

B(3) = 1 3 + 2 3 + 3 3 = 36 =

Tādējādi var pieņemt, ka
B (n) = (1 + 2 + ….+ n) 2 =
(2)

c) Rezultātā par summu А(n) mēs iegūstam

A( n) ==

= (*)

3. Pierādīsim iegūto formulu (*) ar matemātiskās indukcijas metodi.

a) pārbaudiet vienādību (*) n = 1.

A(1) = 2  =2,

Acīmredzot formula (*) ir patiesa, ja n = 1.

b) pieņemsim, ka formula (*) ir patiesa n=k , kur k N, tas ir, vienādība

A(k)=

Pamatojoties uz pieņēmumu, mēs pierādīsim formulas n =k +1 derīgumu. Tiešām,

A(k+1)=

Tā kā formula (*) ir patiesa n =1, un no pieņēmuma, ka tā ir patiesa kādam naturālam k , izriet, ka tā ir patiesa n =k +1, pamatojoties uz matemātiskās indukcijas principu, mēs secinām, ka vienlīdzība

attiecas uz jebkuru dabisko n .

2. uzdevums.

Aprēķiniet summu 1-2 + 3-4 +…(-1) n -1 n .

Risinājums.

Pierakstīsim summu vērtības dažādām n vērtībām pēc kārtas.

A(1)=1, A(2)=1-2=-1, A(3)=1-2+3=2, A(4)=1-2+3-4= -2,

A(5)=1-2+3-4+5=3, A(6)=1-2+3-4+5-6= -3.

Vērojot modeli, varam pieņemt, ka A (n)= - pāra n un A (n)=
par nepāra n. Apvienosim abus rezultātus vienā formulā:

A(n) =
, kur r ir atlikums, dalot n ar 2.

UN r , acīmredzami nosaka šāds noteikums

0 ja n ir pāra,

1 ja n ir nepāra.

Tad r(var uzminēt) var attēlot kā:

Visbeidzot mēs iegūstam formulu A (n):

A(n)=

(*)

Pierādīsim vienādību (*) visiem n  N matemātiskās indukcijas metode.

2. a) Pārbaudiet vienādību (*) n =1. A(1) = 1 =

Vienlīdzība ir godīga

b) Pieņemsim, ka vienādība

1-2+3-4+…+(-1) n-1 n=

taisnība plkst n=k. Pierādīsim, ka tas der arī n =k + 1, t.i.

A(k+1)=

Patiešām,

A(k+1)=A(k)+(-1) k (k+1) =

Q.E.D.

Matemātiskās indukcijas metodi izmanto arī dalāmības problēmu risināšanai.

3. uzdevums.

Pierādīt, ka skaitlis N (n)=n 3 + 5n jebkuram naturālam n dalās ar 6.

Pierādījums.

Plkst n =1 skaitlis N (1)=6, un tāpēc apgalvojums ir patiess.

Lai skaitlis N (k )=k 3 +5k kādam naturālam k dalās ar 6. Pierādīsim, ka N (k +1)= (k +1) 3 + 5(k +1) dalās ar 6. Patiešām, mums ir
N (k +1) = (k +1) 3 + 5 (k +1) = (k 3 +5 k ) + 3 k (k +1) + 6.

Tāpēc ka k un k +1 ir blakus esoši naturāli skaitļi, tad viens no tiem obligāti ir pāra, tāpēc izteiksme 3k (k +1) dalās ar 6. Tādējādi iegūstam, ka N (k +1) arī dalās ar 6. Izvade skaitlis N (n)=n 3 + 5n jebkuram naturālam n dalās ar 6.

Apsveriet sarežģītākas dalāmības problēmas risinājumu, kad vairākas reizes jāpiemēro pilnīgas matemātiskās indukcijas metode.

4. uzdevums.

Pierādiet, ka jebkuram dabiskajam n skaitlim
nav pat dalāms ar 2 n +3 .

Pierādījums.

Iedomājies
darba formā
=

= (*)

Pieņemot, ka (*) pirmais faktors nedalās vienmērīgi ar skaitli 2 k +3 , tas ir, saliktā skaitļa attēlojumā
pirmskaitļu reizinājuma veidā skaitlis 2 atkārtojas ne vairāk kā (k + 2) reizes. Tātad, lai pierādītu, ka skaitlis
nav dalāms ar 2 k +4 , mums tas jāpierāda
nedalās ar 4.

Lai pierādītu šo apgalvojumu, mēs pierādam palīgapgalvojumu: jebkuram naturālam n skaitlis 3 2 n +1 nedalās ar 4. Ja n =1, apgalvojums ir acīmredzams, jo 10 nedalās ar 4 bez atlikuma. Pieņemot, ka 3 2 k +1 nedalās ar 4, pierāda, ka arī 3 2(k +1) +1 nedalās
ar 4. Pēdējo izteiksmi attēlosim kā summu:

3 2(k+1) +1=3 2k+2 +1=3 2k * 9+1=(3 2k +1)+8 * 3 2k . Summas otrais loceklis dalās ar 4, bet pirmais nedalās. Tāpēc visa summa bez atlikuma nedalās ar 4. Palīgapgalvojums ir pierādīts.

Tagad tas ir skaidrs
nedalās ar 4, jo 2k ir pāra skaitlis.

Visbeidzot, mēs iegūstam šo numuru
nav vienmērīgi dalāms ar 2 n +3 jebkuram naturālam n .

Apsveriet tagad piemēru indukcijas pielietošanai nevienlīdzības pierādījumā.

5. uzdevums.

Kuram naturālajam n ir spēkā nevienādība 2 n > 2n + 1?

Risinājums.

1. Kad n=121< 2*1+1,

plkst n=2 2 2< 2*2+1,

plkst n = 3 2 3 > 2*3+1,

plkst n = 4 2 4 > 2*4+1.

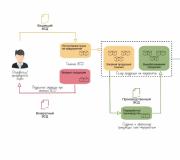
Acīmredzot nevienādība ir spēkā jebkurai dabiskai n  3. Pierādīsim šo apgalvojumu.

2. Kad n =3 nevienādības derīgums jau ir parādīts. Tagad lai nevienādība ir spēkā n =k , kur k ir kāds naturāls skaitlis, kas nav mazāks par 3, t.i.

2 k > 2k+1 (*)

Pierādīsim, ka tad nevienādība ir spēkā arī n =k +1, tas ir, 2 k +1 >2(k +1)+1. Reizinot (*) ar 2, iegūstam 2 k +1 >4k +2. Salīdzināsim izteiksmes 2(k +1)+1 un 4k +2.

4k+2-(2(k+1)+1)=2k-1. Acīmredzot 2k -1>0 jebkuram dabiskajam k . Tad 4k +2>2(k +1)+1, t.i. 2k+1 >2(k+1)+1. Apgalvojums ir pierādīts.

6. uzdevums.

Nevienādība n nenegatīvu skaitļu vidējam aritmētiskajam un ģeometriskajam (Košī nevienādība)., mēs iegūstam =

Ja vismaz viens no numuriem
ir vienāds ar nulli, tad ir spēkā arī nevienādība (**).

Secinājums.

Veicot darbu, izpētīju matemātiskās indukcijas metodes būtību un tās pierādīšanu. Darbā ir izklāstītas problēmas, kurās svarīga loma bija nepilnīgai indukcijai, kas noved pie pareiza risinājuma, un pēc tam tiek veikts pierādījums, kas iegūts ar matemātiskās indukcijas metodi.

Literatūra.

Boltjanskis V.G., Sidorovs Ju.V., Šaburins M.I. Lekcijas un uzdevumi elementārajā matemātikā; Zinātne, 1974.

Viļenkins N.Ya. , Shvartsburd S.I. Matemātiskā analīze.
M.: Izglītība, 1973. gads.

Gaļitskis M.L., Moškovičs M.M., Švartsburds S.I. Padziļināta algebras un matemātiskās analīzes kursa izpēte - M .: Izglītība, 1990.

Potapovs M.K., Aleksandrovs V.V., Pasičenko P.I. Algebra un elementāro funkciju analīze.- M.: Nauka, 1980.

Sominskis I.S., Golovina M.L., Jagloms I.M. Par matemātisko indukciju.- M.: Nauka, 1967.g.

Daudzās matemātikas jomās ir jāpierāda tāda apgalvojuma patiesums, kas ir atkarīgs no , t.i., priekšlikuma patiesums p(n) Priekš " nнN (jebkuram n IESL p(n) pa labi).

To bieži var pierādīt matemātiskās indukcijas metode.

Šīs metodes pamatā ir matemātiskās indukcijas princips. To parasti izvēlas kā vienu no aritmētikas aksiomām un tāpēc pieņem bez pierādījumiem. Saskaņā ar matemātiskās indukcijas principu teikums p(n) tiek uzskatīts par patiesu visām mainīgā lieluma dabiskajām vērtībām, ja ir izpildīti divi nosacījumi:

1. Piedāvājums p(n) patiess priekš n= 1.

2. No teikuma, ka p(n) patiess priekš n =k (k - patvaļīgs naturāls skaitlis), no tā izriet, ka tas ir patiess n =k+ 1.

Ar matemātiskās indukcijas metodi saprot šādu pierādīšanas metodi

1. Pārbaudiet apgalvojuma patiesumu n= 1 ir indukcijas bāze.

2. Pieņemsim, ka apgalvojums ir patiess n = k - induktīvs pieņēmums.

3. Pierādiet, ka tad tas attiecas arī uz n =k+ 1 induktīvā pāreja.

Dažreiz ieteikums p(n) izrādās taisnība ne visiem dabiskajiem n, un sākot no dažiem par n = n 0. Šajā gadījumā indukcijas bāzē tiek pārbaudīta patiesība p(n) plkst n = n 0.

1. piemērsĻaujiet . Pierādiet to

1. Indukcijas bāze: kad n= 1 pēc definīcijas S 1 = 1 un pēc formulas iegūstam vienu rezultātu. Apgalvojums ir pareizs.

n=k Un .

n=k+ 1. Pierādīsim, ka .

Patiešām, pēc induktīvā pieņēmuma

Pārveidosim šo izteiksmi

Induktīvā pāreja ir pierādīta.

komentēt. Ir lietderīgi pierakstīt, kas ir dots (induktīvs pieņēmums) un kas jāpierāda!

2. piemērs Pierādīt

1. Indukcijas bāze. Plkst n= 1, apgalvojums acīmredzami ir patiess.

2. Induktīvs pieņēmums. Ļaujiet n=k Un

3. Induktīvā pāreja. Ļaujiet n=k+ 1. Pierādīsim:

Patiešām, pieņemsim labo pusi kvadrātā kā divu skaitļu summu:

Izmantojot induktīvo pieņēmumu un aritmētiskās progresijas summas formulu: , iegūstam

3. piemērs Pierādiet nevienlīdzību

1. Indukcijas pamats šajā gadījumā ir apgalvojuma patiesuma pārbaude par , t.i. nevienlīdzība ir jāpārbauda. Lai to izdarītu, pietiek ar nevienlīdzības kvadrātu: vai 63< 64 – неравенство верно.

2. Ļaujiet nevienlīdzībai būt patiesai , t.i.

3. Ļaujiet , pierādiet:

Mēs izmantojam indukcijas hipotēzi

Zinot, kādai vajadzētu izskatīties pierādāmās nevienlīdzības labajā pusē, mēs izvēlamies šo daļu

Atliek konstatēt, ka papildu faktors nepārsniedz vienotību. Tiešām,

4. piemērs Pierādiet, ka jebkurš naturāls skaitlis beidzas ar ciparu.

1. Mazākais naturālais skaitlis, no kura apgalvojums ir patiess, ir vienāds ar . .

2. Lai skaitlis beidzas ar . Tas nozīmē, ka šo skaitli var uzrakstīt kā , kur ir kāds naturāls skaitlis. Tad .

3. Ļaujiet . Pierādīsim, ka tas beidzas ar . Izmantojot iegūto attēlojumu, mēs iegūstam

Pēdējam numuram ir tieši vieni.

Pieteikums

1.4. Matemātiskās indukcijas metode

Kā zināms, matemātiskie apgalvojumi (teorēmas) ir jāpamato, jāpierāda. Tagad iepazīsimies ar vienu no pierādīšanas metodēm - matemātiskās indukcijas metodi.

Plašā nozīmē indukcija ir spriešanas veids, kas ļauj pāriet no konkrētiem apgalvojumiem uz vispārīgiem. Apgriezto pāreju no vispārīgiem apgalvojumiem uz konkrētiem sauc par dedukciju.

Dedukcija vienmēr noved pie pareiziem secinājumiem. Piemēram, mēs zinām vispārīgo rezultātu: visi veseli skaitļi, kas beidzas ar nulli, dalās ar 5. No tā, protams, varam secināt, ka jebkurš konkrēts skaitlis, kas beidzas ar 0, piemēram, 180, dalās ar 5.

Tajā pašā laikā indukcija var novest pie nepareiziem secinājumiem. Piemēram, pamanot, ka skaitlis 60 dalās ar skaitļiem 1, 2, 3, 4, 5, 6, mums nav tiesību secināt, ka 60 vispār dalās ar jebkuru skaitli.

Matemātiskās indukcijas metode ļauj daudzos gadījumos stingri pierādīt vispārīgā apgalvojuma P(n) pamatotību, kura formulējumā ir iekļauts naturāls skaitlis n.

Metodes pielietojums ietver 3 posmus.

1) Indukcijas bāze: pārbaudām apgalvojuma P(n) derīgumu, ja n = 1 (vai citai, privātai n vērtībai, no kuras tiek pieņemts P(n) derīgums).

2) Indukcijas pieņēmums: pieņemam, ka P(n) ir patiess, ja n = k.

3) Indukcijas solis: izmantojot pieņēmumu, pierāda, ka P(n) ir patiess, ja n = k + 1.

Rezultātā varam secināt, ka P(n) ir derīgs jebkuram n ∈ N. Patiešām, ja n = 1, apgalvojums ir patiess (indukcijas bāze). Un tāpēc tas attiecas arī uz n = 2, jo pāreja no n = 1 uz n = 2 ir pamatota (indukcijas solis). Atkal un atkal pielietojot indukcijas soli, iegūstam P(n) derīgumu n = 3, 4, 5, . . ., t.i., P(n) derīgums visiem n.

14. piemērs. Pirmo n nepāra naturālu skaitļu summa ir n2: 1 + 3 + 5 + ...

+ (2n - 1) = n2.

Pierādīšana tiks veikta ar matemātiskās indukcijas metodi.

1) Bāze: ja n=1, kreisajā pusē ir tikai viens vārds, mēs iegūstam: 1 = 1.

Apgalvojums ir pareizs.

2) Pieņēmums: pieņemam, ka kādam k vienādība ir patiesa: 1 + 3 + 5 + ... + (2k - 1) = k2.

Problēmu risināšana par sitienu iespējamību šāvienu laikā

Problēmas vispārīgais izklāsts ir šāds:

Varbūtība trāpīt mērķī ar vienu šāvienu ir vienāda ar $p$. $n$ šāvieni. Atrodiet varbūtību, ka mērķis tiks trāpīts tieši $k$ reizes (būs $k$ sitieni).

Mēs izmantojam Bernulli formulu un iegūstam:

$$ P_n(k)=C_n^k \cdot p^k \cdot (1-p)^(n-k) = C_n^k \cdot p^k \cdot q^(n-k).

Šeit $C_n^k$ ir kombināciju skaits no $n$ līdz $k$.

Ja problēma ir saistīta ar vairākām bultiņām ar dažādas varbūtības trāpīšana mērķī, teorija, risinājumu piemēri un kalkulators, ko varat atrast šeit.

Video apmācība un Excel veidne

Noskatieties mūsu video par problēmu risināšanu ar Bernulli kadriem, uzziniet, kā izmantot Excel, lai atrisinātu izplatītas problēmas.

Excel aprēķinu failu no video var lejupielādēt bez maksas un izmantot savu problēmu risināšanai.

Piemēri problēmu risināšanai par sitienu mērķī šāvienu sērijā

Apskatīsim dažus tipiskus piemērus.

1. piemērs Izšāva 7 šāvienus. Iespēja trāpīt ar vienu metienu ir 0,705. Atrodiet varbūtību, ka būs tieši 5 trāpījumi.

Iegūstam, ka problēma ir saistīta ar atkārtotiem neatkarīgiem testiem (šāvieni mērķī), kopā tiek izšauti $n=7$ šāvieni, varbūtība trāpīt ar katru $p=0,705$, varbūtība izlaist $q=1-p = 1-0,705 = 0,295 USD.

Mums jāatrod, ka būs tieši $k=5$ trāpījumi. Mēs visu aizstājam formulā (1) un iegūstam: $$ P_7(5)=C_(7)^5 \cdot 0.705^5 \cdot 0.295^2 = 21\cdot 0.705^5 \cdot 0.295^2= 0.318. $$

2. piemērs Varbūtība trāpīt mērķī ar vienu šāvienu ir 0,4.

Uz mērķi tiek raidīti četri neatkarīgi šāvieni. Atrodiet varbūtību, ka mērķī tiks trāpīts vismaz viens.

Izpētām uzdevumu un pierakstām parametrus: $n=4$ (šāviens), $p=0.4$ (trāpījuma varbūtība), $k \ge 1$ (būs vismaz viens trāpījums).

Mēs izmantojam pretēja notikuma varbūtības formulu (nav trāpījuma):

$$ P_4(k \ge 1) = 1-P_4(k \lt 1) = 1-P_4(0) = $$ $$ =1-C_(4)^0 \cdot 0.4^0 \cdot 0,6 ^4 =1-0,6^4=1-0,13=0,87. $$

Varbūtība trāpīt vismaz reizi četros ir 0,87 jeb 87%.

3. piemērs Varbūtība, ka šāvējs trāpīs mērķī, ir 0,3.

Atrodi varbūtību, ka ar 6 šāvieniem mērķī tiks trāpīts trīs līdz sešas reizes.

Atšķirībā no iepriekšējām problēmām, šeit ir jāatrod iespējamība, ka trāpījumu skaits būs noteiktā intervālā (un ne precīzi vienāds ar kādu skaitli). Bet formula ir tāda pati.

Atradīsim varbūtību, ka mērķī tiks trāpīts no trīs līdz sešām reizēm, tas ir, būs vai nu 3, vai 4, vai 5, vai 6 sitieni.

Šīs varbūtības aprēķina pēc formulas (1):

$$ P_6(3)=C_(6)^3 \cpunkts 0,3^3\cpunkts 0,7^3 = 0,185. $$ $$ P_6(4)=C_(6)^4 \cpunkts 0,3^4\cpunkts 0,7^2 = 0,06. $$ $$ P_6(5)=C_(6)^5 \cpunkts 0,3^5\cpunkts 0,7^1 = 0,01. $$ $$ P_6(6)=C_(6)^6 \cpunkts 0,3^6\cpunkts 0,7^0 = 0,001.

Tā kā notikumi nav savietojami, vēlamo varbūtību var atrast, izmantojot varbūtību saskaitīšanas formulu: $$ P_6(3 \le k \le 6)=P_6(3)+P_6(4)+P_6(5)+P_6(6) =$$$$ = 0,185+0,06+0,01+0,001=0,256.$$

4. piemērs Vismaz viena trāpījuma iespēja ar četriem šāvieniem mērķī ir 0,9984. Atrodi varbūtību trāpīt mērķī ar vienu šāvienu.

Apzīmēsim varbūtību trāpīt mērķī ar vienu šāvienu. Ievadīsim notikumu:
$A = $ (no četriem šāvieniem vismaz viens trāpīs mērķī),
kā arī tā pretējais notikums, ko var uzrakstīt šādi:
$\overline(A) = $ (Visi 4 šāvieni netrāpīs mērķī, nav trāpījumu).

Pierakstīsim notikuma $A$ varbūtības formulu.

Pierakstīsim zināmās vērtības: $n=4$, $P(A)=0,9984$. Aizvietojiet formulā (1) un iegūstiet:

$$ P(A)=1-P(\overline(A))=1-P_4(0)=1-C_(4)^0 \cdot p^0 \cdot (1-p)^4=1- (1-p)^4=0,9984.

Mēs atrisinām iegūto vienādojumu:

$ 1-(1-p)^4=0,9984,\\ (1-p)^4=0,0016,\\ 1-p=0,2,\\ p=0,8. $$

Tātad varbūtība trāpīt mērķī ar vienu šāvienu ir 0,8.

Paldies, ka lasījāt un dalījāties ar citiem

Noderīgas saites

Risinājumā atrodiet gatavus uzdevumus:

Tiešsaistes aprēķini, izmantojot Bernulli formulu

Nevienādības atrisināšana ar kalkulatoru

Nevienlīdzība matemātikā attiecas uz visiem vienādojumiem, kur "="" aizstāj ar jebkuru no šīm rakstzīmēm: \ [> \] \ [\geq \] \ [

* lineārs;

* kvadrāts;

* daļskaitlis;

* orientējoši;

* trigonometrisks;

* logaritmisks.

Atkarībā no tā nevienādības sauc par lineārām, daļējām utt.

Jums jāzina šādas pazīmes:

* nevienādības ar lielāku par (>) vai mazāku par (

* Nevienādības ar ikonām, kas ir lielākas vai vienādas ar \[\geq\] mazākas vai vienādas ar [\leq\], tiek sauktas par neprofesionālām;

* ikona nav viena un tā pati \[\ne\], bet gadījumi ar šo ikonu ir jāatrisina visu laiku.

Šāda nevienlīdzība tiek atrisināta ar identitāšu transformācijām.

Izlasiet arī mūsu rakstu "Tiešsaistes vienādojuma pilnīga risinājuma atrisināšana"

Pieņemsim, ka pastāv šāda nevienlīdzība:

Mēs to atrisinām tāpat kā lineāro vienādojumu, taču mums rūpīgi jāuzrauga nevienlīdzības zīme.

Pirmkārt, mēs pārvietojam terminus no nezināmā uz kreiso pusi, no zināmā uz labo, apgriežot simbolus:

Pēc tam abas puses sadalām ar -4 un apgriežam nevienlīdzības zīmi:

Šī ir atbilde uz šo vienādojumu.

Kur es varu atrisināt nevienlīdzību internetā?

Jūs varat atrisināt vienādojumu mūsu vietnē pocketteacher.ru.

Bernulli nevienlīdzības kalkulators

Dažu sekunžu laikā bezmaksas tiešsaistes glābšanas risinājums atrisinās jebkuras sarežģītības tiešsaistes vienādojumu. Viss, kas jums jādara, ir ievadiet savus datus glābšanā. Mūsu vietnē varat arī noskatīties video instrukcijas un uzzināt, kā atrisināt vienādojumu.

Un, ja jums ir jautājumi, varat tos uzdot mūsu Vkontakte grupā: pocketteacher. Pievienojieties mūsu grupai, mēs ar prieku jums palīdzēsim.

Pilnas matemātiskās indukcijas metode

Vienādojumu risināšana / Diferenciālvienādojumi

Diferenciālvienādojumu risinājums

Ievadiet atšķir.
vienādojums:

Ar kalkulatoru varat atrisināt dažādas sarežģītības diferenciālvienādojumus.

Pierādīt ar matemātisko indukciju. Matemātiskās indukcijas metode un tās pielietojums problēmu risināšanā

Indukcija un dedukcija.

Matemātiskās indukcijas metode.

Vienādojumu un nevienādību pierādījumu piemēri ar matemātiskās indukcijas metodi.

Ievads.

Matemātiskās indukcijas princips un tā pierādījums

Indukcija algebrā

Apsveriet vairākus algebrisko problēmu piemērus, kā arī dažādu nevienādību pierādījumus, kurus var atrisināt, izmantojot matemātiskās indukcijas metodi.

6. uzdevums.

Secinājums.

Literatūra.

Problēmu risināšana par sitienu iespējamību šāvienu laikā

Video apmācība un Excel veidne

Piemēri problēmu risināšanai par sitienu mērķī šāvienu sērijā

Noderīgas saites

Nevienādības atrisināšana ar kalkulatoru

Kur es varu atrisināt nevienlīdzību internetā?

Bernulli nevienlīdzības kalkulators

Pilnas matemātiskās indukcijas metode

Diferenciālvienādojumu risinājums

Ievadiet atšķir. vienādojums:

Atrisināto diferenciālvienādojumu piemēri

Ievadiet atšķir.
vienādojums: