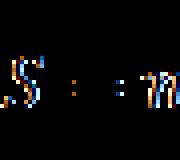Mrežni kalkulator relativne pogreške. Relativna greška

3.1 Pogreška aritmetičke sredine. Kao što je ranije navedeno, mjerenja u osnovi ne mogu biti apsolutno točna. Stoga se tijekom mjerenja javlja problem određivanja intervala u kojem se najvjerojatnije nalazi prava vrijednost mjerene veličine. Takav interval je označen kao apsolutna greška mjerenja.

Ako pretpostavimo da su grube pogreške u mjerenjima eliminirane, a sustavne pogreške pomnim ugađanjem instrumenata i cijele instalacije minimizirane i nisu presudne, tada će rezultati mjerenja uglavnom sadržavati samo slučajne pogreške, a to su predznakoizmjenične vrijednosti. Dakle, ako se provodi više ponovljenih mjerenja iste veličine, tada je najvjerojatnija vrijednost izmjerene veličine njezina aritmetička sredina:

Prosječna apsolutna greška naziva se aritmetička sredina modula apsolutne pogreške pojedinačnih mjerenja:

Posljednja nejednakost obično se piše kao konačni rezultat mjerenja na sljedeći način:

(5)

pri čemu apsolutnu pogrešku a cf treba izračunati (zaokružiti) na jednu ili dvije značajne znamenke. Apsolutna pogreška pokazuje koji predznak broja sadrži netočnosti, dakle, u izrazu za vjenčanje ostavite sve točne brojeve i jedan upitan. To jest, prosječna vrijednost i prosječna pogreška izmjerene vrijednosti moraju se izračunati na istu znamenku iste znamenke. Na primjer: g = (9,78 ± 0,24) m/s 2.

Relativna greška. Apsolutna pogreška određuje interval najvjerojatnijih vrijednosti izmjerene vrijednosti, ali ne karakterizira stupanj točnosti mjerenja. Na primjer, udaljenost između naselja, mjereno s točnošću od nekoliko metara, može se pripisati vrlo preciznim mjerenjima, dok će mjerenje promjera žice s točnošću od 1 mm, u većini slučajeva, biti vrlo približno mjerenje.

Stupanj točnosti izvedenih mjerenja karakterizira relativna pogreška.

sredina relativna pogreška ili jednostavno relativna mjerna pogreška je omjer prosječne apsolutne mjerne pogreške i prosječne vrijednosti izmjerene veličine:

Relativna pogreška je bezdimenzijska veličina i obično se izražava u postocima.

3.2 Greška metode ili instrumentalna greška. Aritmetička srednja vrijednost izmjerene veličine je to bliža stvarnoj što se više mjerenja vrši, dok apsolutna pogreška mjerenja s porastom njihovog broja teži vrijednosti koja je određena metodom mjerenja i Tehničke specifikacije korištenih uređaja.

Greška metode ili se pogreška instrumenta može izračunati iz jednog mjerenja, poznavajući klasu točnosti instrumenta ili druge podatke tehnička putovnica instrument, koji označava ili klasu točnosti instrumenta, ili njegovu apsolutnu ili relativnu grešku mjerenja.

Klasa točnosti instrument izražava u postotku nominalni relativna pogreška uređaja, odnosno relativnu grešku mjerenja kada je izmjerena vrijednost jednaka graničnoj vrijednosti za ovaj uređaj

Apsolutna pogreška uređaja ne ovisi o vrijednosti mjerene veličine.

Relativna pogreška instrumenta (prema definiciji):

(10)

odakle se vidi da je relativna instrumentalna pogreška tim manja bliže značenje izmjerenu vrijednost do granice mjerenja ovog uređaja. Stoga se preporučuje odabir uređaja tako da izmjerena vrijednost bude 60-90% vrijednosti za koju je uređaj predviđen. Pri radu s višegraničnim instrumentima također treba nastojati osigurati da se očitanje vrši u drugoj polovici ljestvice.

Pri radu s jednostavnim instrumentima (ravnalo, čaša itd.), čije klase točnosti i pogreške nisu određene tehničkim karakteristikama, uzima se apsolutna pogreška izravnih mjerenja. pola podjela skale ovog uređaja. (Cijena podjele je vrijednost izmjerene količine kada instrument očitava u jednom podjelu).

Instrumentalna pogreška neizravnih mjerenja može se izračunati korištenjem pravila aproksimacije. Izračun pogreške neizravnih mjerenja temelji se na dva uvjeta (pretpostavke):

1. Apsolutne pogreške mjerenja uvijek su vrlo male u usporedbi s izmjerenim vrijednostima. Stoga se apsolutne pogreške (u teoriji) mogu smatrati infinitezimalnim priraštajima izmjerenih veličina, a mogu se zamijeniti odgovarajućim diferencijalima.

2. Ako je fizikalna veličina koja se utvrđuje neizravno funkcija jedne ili više izravno mjerenih veličina, tada je apsolutna pogreška funkcije, zbog infinitezimalnih inkremenata, također infinitezimalna veličina.

Pod ovim pretpostavkama, apsolutne i relativne pogreške mogu se izračunati korištenjem dobro poznatih izraza iz teorije diferencijalnog računa funkcija mnogih varijabli:

	(11)
	(12)

Apsolutne pogreške izravnih mjerenja mogu imati predznak plus ili minus, ali nije poznato koji. Stoga se pri određivanju pogrešaka smatra najnepovoljnijim slučajem kada pogreške izravnih mjerenja pojedinih veličina imaju isti predznak, odnosno apsolutna pogreška ima najveću vrijednost. Stoga se pri računanju priraštaja funkcije f(x 1 ,x 2 ,…,h n) prema formulama (11) i (12), parcijalni prirasti moraju se dodati u apsolutnoj vrijednosti. Dakle, korištenjem aproksimacije Dh i ≈ dx i , i izraze (11) i (12), za infinitezimalne inkremente Da može se napisati:

	(13)
	(14)

Ovdje: A - neizravno mjerena fizikalna veličina, odnosno određena računskom formulom, Da je apsolutna greška njegovog mjerenja, x 1, x 2,... x n; Dh 1, Dx 2 ,..., Dh n ,- fizikalne veličine izravnih mjerenja, odnosno njihove apsolutne pogreške.

Dakle: a) apsolutna pogreška neizravne metode mjerenja jednaka je zbroju modula umnožaka parcijalnih derivacija mjerne funkcije i odgovarajućih apsolutnih pogrešaka izravnih mjerenja; b) relativna pogreška neizravne metode mjerenja jednaka je zbroju modula diferencijala iz logaritma prirodna funkcija mjerenje određeno računskom formulom.

Izrazi (13) i (14) omogućuju izračunavanje apsolutne i relativne pogreške iz jednog mjerenja. Imajte na umu da je za smanjenje izračuna pomoću navedenih formula dovoljno izračunati jednu od pogrešaka (apsolutnu ili relativnu), a drugu izračunati pomoću jednostavnog odnosa između njih:

(15)

U praksi se češće koristi formula (13), budući da se kod logaritmiranja formule za izračun umnošci raznih veličina pretvaraju u odgovarajuće zbrojeve, a potencijska i eksponencijalna funkcija u umnoške, što znatno pojednostavljuje proces diferencijacije.

Za praktične smjernice za izračunavanje nesigurnosti neizravne mjerne metode može se koristiti sljedeće pravilo:

Za izračun relativne pogreške neizravne metode mjerenja potrebno je:

1. Odredite apsolutne pogreške (instrumentalne ili prosječne) izravnih mjerenja.

2. Uzmite logaritam izračunate (radne) formule.

3. Uzimajući vrijednosti izravnih mjerenja kao nezavisne varijable, pronađite ukupni diferencijal iz rezultirajućeg izraza.

4. Zbrojite sve parcijalne razlike u apsolutnim vrijednostima, zamjenjujući varijable razlike u njima odgovarajućim apsolutnim pogreškama izravnih mjerenja.

Na primjer, gustoća cilindričnog tijela izračunava se po formuli:

(16)

Gdje m, D, h - izmjerene količine.

Dobivamo formulu za izračunavanje pogrešaka.

1. Na temelju korištene opreme utvrđujemo apsolutne pogreške u mjerenju mase, promjera i visine cilindra (∆m, ∆D, ∆h odnosno).

2. Logaritmiramo izraz (16):

3. Razlikovati:

4. Zamjenom diferencijala nezavisnih varijabli s apsolutnim pogreškama i dodavanjem modula parcijalnih inkremenata dobivamo:

5. Korištenje numeričkih vrijednosti m, D, h, D, m, h, očekujemo E.

6. Izračunajte apsolutnu pogrešku

Gdje r izračunati po formuli (16).

Pozivamo vas da se sami uvjerite da u slučaju šupljeg cilindra ili cijevi s unutarnjim promjerom D1 i vanjski promjer D2

Izračunu pogreške mjerne metode (izravne ili neizravne) potrebno je pribjeći u slučajevima kada višestruka mjerenja nije moguće izvesti pod istim uvjetima ili dugo traju.

Ako je određivanje pogreške mjerenja temeljni zadatak, tada se mjerenja obično provode opetovano i izračunavaju se i pogreška aritmetičke sredine i pogreška metode (pogreška instrumenta). U konačnom rezultatu označite najveći od njih.

O točnosti izračuna

Pogreška rezultata određena je ne samo netočnostima mjerenja, već i netočnostima izračuna. Izračuni se moraju izvesti tako da je njihova pogreška za red veličine manja od pogreške rezultata mjerenja. Da biste to učinili, zapamtite pravila matematička radnja s bliskim brojevima.

Rezultati mjerenja su približni brojevi. U okvirnom broju svi brojevi moraju biti točni. Posljednja točna znamenka približnog broja je takva znamenka čija pogreška ne prelazi jednu jedinicu znamenke. Sve znamenke od 1 do 9 i 0, ako je u sredini ili na kraju broja, nazivaju se značajnim. U broju 2330 postoje 4 značajne znamenke, au broju 6,1 × 10 2 - samo dvije, u broju 0,0503 - tri, jer su nule lijevo od pet beznačajne. Upisivanje broja 2,39 znači da su svi znakovi do drugog iza decimalne točke točni, a upisivanje 1,2800 znači da su i treći i četvrti znak točni. U broju 1,90 postoje tri značajne znamenke, što znači da smo pri mjerenju uzeli u obzir ne samo jedinice, već i desetinke i stotinke, a u broju 1,9 samo dvije značajne brojke, što znači da smo uzeli u obzir cijele brojeve i desetinke. a točnost je ovaj broj 10 puta manji.

Pravila zaokruživanja brojeva

Prilikom zaokruživanja ostavljaju se samo ispravni znakovi, ostali se odbacuju.

1. Zaokruživanje se postiže jednostavnim odbacivanjem znamenki ako je prva od odbačenih znamenki manja od 5.

2. Ako je prva od odbačenih znamenki veća od 5, tada se zadnja znamenka povećava za jedan. Posljednja znamenka se također povećava kada je prva od odbačenih znamenki 5 nakon koje slijedi jedna ili više znamenki različitih od nule.

Na primjer, različita zaokruživanja broja 35,856 bila bi: 35,9; 36.

3. Ako je odbačena znamenka 5, a iza nje nema značajnih znamenki, tada se zaokružuje na najbliži paran broj, odnosno zadnja znamenka koja se sprema ostaje nepromijenjena ako je parna i povećava se za jedan ako je neparan.

Na primjer, 0,435 zaokružuje se na 0,44; 0,365 zaokružuje se na 0,36.

Apsolutne i relativne pogreške

Moramo se nositi s približnim brojevima kada izračunavamo vrijednosti bilo koje funkcije ili kada mjerimo i obrađujemo fizičke veličine dobivene kao rezultat eksperimenata. U oba slučaja morate znati ispravno zapisati vrijednosti približnih brojeva i njihovu pogrešku.

Približan broj A zove se broj koji se malo razlikuje od točnog broja A i zamjenjuje potonje u proračunima. Ako se zna da A< А , To A naziva se približna vrijednost broja A nedostatkom; Ako a > a, - tada u višku. Ako A je približna vrijednost broja A, onda pišu a ≈ A.

Pod greškom ili greškom A približan broj A obično se shvaća kao razlika između odgovarajućeg točnog broja A i zadane približne, tj.

Da bismo dobili točan broj A, potrebno je dodati njegovu grešku približnoj vrijednosti broja, tj.

U mnogim slučajevima, znak greške je nepoznat. Tada je preporučljivo koristiti apsolutnu pogrešku približnog broja

Iz gornjeg unosa proizlazi da je apsolutna pogreška približnog broja A naziva se modul razlike između odgovarajućeg točnog broja A i njegovu približnu vrijednost A, tj.

Točan broj A najčešće je nepoznata, pa nije moguće pronaći pogrešku ili apsolutnu pogrešku. U tom slučaju, umjesto nepoznate teorijske pogreške, korisno je uvesti njezinu gornju procjenu, tzv. graničnu apsolutnu pogrešku.

Pod graničnom apsolutnom pogreškom približnog broja A podrazumijeva se svaki broj koji nije manji od apsolutne pogreške tog broja, tj.

Ako u zadnjem unosu umjesto formule (1.1), možemo napisati

(1.2)

Iz toga proizlazi da točan broj A sadržano unutar granica

Dakle, razlika je aproksimacija broja A nedostatkom, i - aproksimacija broja A u visku. U ovom slučaju, radi sažetosti, koristimo oznaku

Jasno je da je granična apsolutna pogreška definirana dvosmisleno: ako je određeni broj granična apsolutna pogreška, tada je svaki veći od pozitivnog broja također granična apsolutna pogreška. U praksi se nastoji izabrati najmanji i najjednostavniji mogući broj , koji zadovoljava nejednakost (1.2).

Na primjer, ako smo kao rezultat mjerenja dobili duljinu segmenta l\u003d 210 cm ± 0,5 cm, onda je ovdje granična apsolutna pogreška = 0,5 cm, te točnu vrijednost l segment je zatvoren unutar granica od 209,5 cm ≤l≤ 210,5 cm.

Apsolutna pogreška nije dovoljna za karakterizaciju točnosti mjerenja ili izračuna. Tako npr. ako se pri mjerenju duljina dva štapa dobiju rezultati l 1= 95,6 cm ± 0,1 cm i l 2= 8,3 ± 0,1 cm, tada je, unatoč slučajnosti graničnih apsolutnih pogrešaka, točnost prvog mjerenja veća od druge. To pokazuje da je za točnost mjerenja važnija ne apsolutna, već relativna pogreška, koja ovisi o vrijednostima izmjerenih veličina.

Relativna greška δ približan broj A je omjer apsolutne pogreške ovog broja i modula odgovarajućeg točnog broja A, oni.

Slično graničnoj apsolutnoj pogrešci, definicija se također koristi za graničnu relativnu pogrešku. Granična relativna pogreška ovog približnog broja A naziva se bilo koji broj koji nije manji od relativne pogreške tog broja

oni. odakle slijedi

Dakle, za graničnu apsolutnu pogrešku broja A može se prihvatiti

Pošto u praksi A≈a, tada se umjesto formule (1.3) često koristi formula

1.2 Decimalni zapis približnih brojeva

Svaka pozitiva decimalni broj a može se prikazati kao konačni ili beskonačni razlomak

gdje su decimalne znamenke broja A( = 0,1,2,...,9), a najviša znamenka a m- broj znamenki u cijelom dijelu broja A, A n- broj znamenki u zapisu razlomačkog dijela broja A. Na primjer:

5214,73... = 5 10 3 + 2 10 2 + 1 10 1 + 4 10 0 +7 10 -1 + 3 10 -2 ... (1,5)

Svaka znamenka na određenom mjestu u broju A napisano u obliku (1.4) ima svoju težinu. Dakle, broj na prvom mjestu (tj.) teži 10 m, na drugom - 10 m-1 itd.

U praksi se najčešće ne koristi zapis u obliku (1.4), već se koristi skraćeni zapis brojeva u obliku niza koeficijenata pri odgovarajućim potencijama broja 10. ovaj broj u potencijama broja 10.

U praksi se uglavnom radi s približnim brojevima u obliku konačnih decimalni razlomci. Za ispravnu usporedbu različitih računskih i eksperimentalnih rezultata uvodi se koncept značajna znamenka u rezultatskom zapisniku. svi spremljeno decimalne vrijednosti ( i = m,m- 1,…, m-n+ 1) osim nule i nula ako je između značajnih znamenki ili je predstavnik pohranjenog decimalnog mjesta na kraju broja nazivaju se značajnim znamenkama približnog broja A. U ovom slučaju, nule povezane s faktorom 10 n nisu značajni.

Uz položajnu oznaku broja A u decimalnom brojevnom sustavu ponekad morate unijeti dodatne nule na početku ili kraju broja. Na primjer,

A= 7 10 -3 + 0 10 -4 + 1 10 -5 + 0 10 -6 = 0,00 7010

b= 2 10 9 + 0 10 8 + 0 10 7 + 3 10 6 + 0 10 5 = 2003000000.

Takve nule (podvučene u primjerima) ne smatraju se značajnim znamenkama.

Značajna znamenka približnog broja je svaka znamenka u njegovom decimalnom prikazu koja je različita od nule.,kao i nula ako se nalazi između značajnih znamenki ili je predstavnik pohranjenog decimalnog mjesta. Sve ostale nule koje su dio približnog broja i služe samo za označavanje njegovih decimalnih mjesta ne računaju se kao značajni brojevi.

Na primjer, u broju 0,002080 prve tri nule nisu značajne znamenke, jer služe samo za određivanje decimalnih mjesta ostalih znamenki. Preostale dvije nule su značajne znamenke, budući da je prva između značajnih znamenki 2 i 8, a druga označava da je decimalno mjesto 10 -6 pohranjeno u približnom broju. Ako u danom broju 0,002080 posljednja znamenka nije značajna, tada taj broj treba napisati kao 0,00208. S ove točke gledišta, brojevi 0,002080 i 0,00208 nisu ekvivalentni, jer prvi od njih sadrži četiri značajne znamenke, a drugi samo tri.

Uz pojam značajne figure, pojam o točan broj. Treba napomenuti da ovaj koncept postoji u dvije definicije - u suziti I široki smisao.

Definicija(u širem smislu) . To kažu n prve značajne znamenke broja (brojeći s lijeva na desno) su vjeran u širokom smislu, ako apsolutna greška ovog broja ne prelazi jedinicu (težinu) n- vruće pražnjenje. (Objašnjenje: 1 10 1 - ovdje je težina 1 jednaka 10; 1 10 0 - ovdje je težina 1 jednaka 1; 1 10 -1 - ovdje je težina 1 jednaka 0,1; 1 10 -2 - ovdje je težina 1 jednaka do 0,01 i t .d.).

Definicija(u užem smislu). To kažu n prve značajne znamenke približnog broja su točne ako apsolutna pogreška ovog broja ne prelazi pola jedinice (težina) n- vruće pražnjenje. (Objašnjenje: 1 10 1 - ovdje je težina polovice 1 5; 1 10 0 - ovdje je težina polovice 1 0,5; 1 10 -1 - 0,05 itd.).

Na primjer, u približnom broju Na temelju prve definicije, značajni brojevi 3,4 i 5 su točni u širem smislu, a broj 6 je dvojben. Na temelju druge definicije, značajni brojevi 3 i 4 točni su u užem smislu, a brojevi 5 i 6 dvojbeni. Važno je naglasiti da točnost približnog broja ne ovisi o broju značajnih znamenki, već o broju ispraviti značajne znamenke.

Kako u teorijskom promišljanju tako i u praktične aplikacije definicija ispravne figure u užem smislu nalazi više primjene.

Dakle, ako za približan broj a, zamjena broja A, poznato je da

(1.6)

zatim, po definiciji, prvi n brojevima ovaj broj je točan.

Na primjer, za točan broj A= 35,97 broj A= 36,00 je aproksimacija s tri valjane znamenke. Sljedeće razmišljanje dovodi do ovog rezultata. Budući da je apsolutna pogreška našeg približnog broja 0,03, po definiciji mora zadovoljiti uvjet

(1.7)

U našem približnom broju 36,00, 3 je prva značajna znamenka (tj. ), tako da m= 1. Dakle, očito je da će uvjet (1.7) biti zadovoljen za n = 3.

Obično se uzima kada se decimalni zapis približnog broja piši samo točne brojeve. Ako se zna da je ovaj približni broj točno napisan, tada se iz zapisa može utvrditi najveća apsolutna pogreška. Kod ispravnog bilježenja apsolutna pogreška ne prelazi polovicu najmanje značajne znamenke koja slijedi iza zadnje točne znamenke (ili polovicu jedinice zadnje točne znamenke, koja je ista)

Na primjer, dani približni brojevi ispravno napisani: a = 3,8; b= 0,0283; c = 4260. Prema definiciji, granične apsolutne pogreške ovih brojeva bit će: = 0,05; = 0,00005; = 0,5.

Fizičke veličine karakteriziraju koncept "točnosti pogreške". Postoji izreka da se mjerenjem dolazi do znanja. Tako će se moći saznati koja je visina kuće ili duljina ulice, kao i mnoge druge.

Uvod

Razumimo značenje pojma "mjeriti vrijednost". Proces mjerenja je usporedba s homogenim veličinama, koje se uzimaju kao jedinica.

Litre se koriste za određivanje volumena, grami se koriste za izračunavanje mase. Radi lakšeg izračunavanja uveli smo SI sustav međunarodna klasifikacija jedinice.

Za mjerenje duljine močvare u metrima, mase - kilogramima, volumena - kubičnim litrama, vremena - sekundama, brzine - metrima u sekundi.

Pri računanju fizičkih veličina nije uvijek potrebno koristiti tradicionalan način, dovoljno je primijeniti izračun pomoću formule. Na primjer, da biste izračunali pokazatelje kao što je prosječna brzina, morate prijeđenu udaljenost podijeliti s vremenom provedenim na cesti. Tako se računa prosječna brzina.

Koristeći mjerne jedinice koje su deset, sto, tisuću puta veće od pokazatelja prihvaćenih mjernih jedinica, nazivaju se višestruki.

Naziv svakog prefiksa odgovara njegovom broju množitelja:

Deca.
Hecto.
Kilo.
Mega.
Giga.
Tera.

U fizikalnoj znanosti za pisanje takvih faktora koristi se potencija broja 10. Na primjer, milijun se označava kao 10 6 .

U jednostavnom ravnalu duljina ima mjernu jedinicu - centimetar. 100 puta je manji od metra. Ravnalo od 15 cm dugo je 0,15 m.

Ravnalo je najjednostavnija vrsta mjernog instrumenta za mjerenje duljine. Složenije uređaje predstavljaju termometar - tako da higrometar - za određivanje vlažnosti, ampermetar - za mjerenje razine sile kojom se širi električna struja.

Koliko će točna biti mjerenja?

Uzmite ravnalo i jednostavnu olovku. Naš zadatak je izmjeriti duljinu ovog pribora.

Prvo morate odrediti koja je cijena podjele navedena na ljestvici mjerni uređaj. Na dva podjeljka, koji su najbliži potezi ljestvice, ispisani su brojevi, na primjer, "1" i "2".

Potrebno je izračunati koliko se podjela nalazi unutar intervala ovih brojeva. Ako dobro brojite, dobit ćete "10". Od broja koji je veći oduzmite broj koji će biti manji i podijelite s brojem koji čini razdjelnike između znamenki:

(2-1)/10 = 0,1 (cm)

Tako utvrđujemo da je cijena koja određuje podjelu dopisnice broj 0,1 cm ili 1 mm. Jasno je prikazano kako se pomoću bilo kojeg mjernog uređaja utvrđuje pokazatelj cijene za podjelu.

Mjerenjem olovke duljine nešto manje od 10 cm iskoristit ćemo stečeno znanje. Da nema malih podjela na ravnalu, zaključak bi bio da predmet ima duljinu od 10 cm.Ovu približnu vrijednost nazivamo greškom mjerenja. Označava razinu netočnosti koja se može tolerirati u mjerenju.

Određivanje parametara duljine olovke s više visoka razina točnosti, većom vrijednošću podjele postiže se veća točnost mjerenja, što daje manju pogrešku.

U ovom slučaju nije moguće izvršiti apsolutno točna mjerenja. A pokazatelji ne bi trebali prelaziti veličinu cijene podjele.

Utvrđeno je da dimenzije pogreške mjerenja iznose ½ cijene koja je navedena na podjelama instrumenta kojim se određuju dimenzije.

Nakon mjerenja olovke na 9,7 cm, određujemo pokazatelje njegove pogreške. Ovo je razmak od 9,65 - 9,85 cm.

Formula koja mjeri takvu pogrešku je izračun:

A = a ± D (a)

A - u obliku veličine za mjerne procese;

a - vrijednost rezultata mjerenja;

D - oznaka apsolutne pogreške.

Prilikom oduzimanja ili dodavanja vrijednosti s pogreškom, rezultat će biti jednak je zbroju indikatori greške, što je svaka pojedinačna vrijednost.

Uvod u koncept

Ako uzmemo u obzir ovisno o načinu izražavanja, možemo razlikovati sljedeće sorte:

Apsolutno.
Relativni.
S obzirom.

Apsolutna greška mjerenja označena je velikim slovom "Delta". Ovaj koncept se definira kao razlika između izmjerene i stvarne vrijednosti fizikalne veličine koja se mjeri.

Izraz apsolutne pogreške mjerenja su jedinice veličine koju treba izmjeriti.

Pri mjerenju mase ona će se izražavati npr. u kilogramima. Ovo nije standard točnosti mjerenja.

Kako izračunati pogrešku izravnih mjerenja?

Postoje načini za predstavljanje grešaka mjerenja i njihovo izračunavanje. Da biste to učinili, važno je moći odrediti fizikalnu veličinu s potrebnom točnošću, znati kolika je apsolutna pogreška mjerenja, koju nitko nikada neće moći pronaći. Možete izračunati samo njegovu graničnu vrijednost.

Čak i ako je ovaj termin uvjetno korišten, on označava upravo granične podatke. Apsolutne i relativne pogreške mjerenja označene su istim slovima, razlika je u njihovom pisanju.

Pri mjerenju duljine apsolutna pogreška mjerit će se u onim jedinicama u kojima se duljina računa. A relativna pogreška izračunava se bez dimenzija, jer je to omjer apsolutne pogreške i rezultata mjerenja. Ta se vrijednost često izražava kao postotak ili razlomci.

Apsolutnih i relativnih grešaka mjerenja ima nekoliko različiti putevi proračuni ovisno o tome koje fizičke veličine.

Pojam izravnog mjerenja

Apsolutna i relativna pogreška izravnih mjerenja ovise o klasi točnosti uređaja i mogućnosti određivanja pogreške vaganja.

Prije nego što govorimo o tome kako se greška izračunava, potrebno je razjasniti definicije. Izravno mjerenje je mjerenje kod kojeg se rezultat izravno očitava sa skale instrumenta.

Kada koristimo termometar, ravnalo, voltmetar ili ampermetar, uvijek provodimo izravna mjerenja, budući da izravno koristimo uređaj s vagom.

Dva su čimbenika koja utječu na izvedbu:

Greška instrumenta.
Greška referentnog sustava.

Apsolutna granica pogreške za izravna mjerenja bit će jednaka zbroju pogreške koju uređaj pokazuje i pogreške koja se javlja tijekom procesa očitavanja.

D = D (pr.) + D (odsutan)

Primjer medicinskog termometra

Vrijednosti točnosti naznačene su na samom instrumentu. Na medicinskom toplomjeru zabilježena je pogreška od 0,1 stupnja Celzijusa. Pogreška čitanja je polovica vrijednosti dijeljenja.

D = C/2

Ako je vrijednost podjele 0,1 stupanj, tada se za medicinski termometar mogu napraviti izračuni:

D \u003d 0,1 o C + 0,1 o C / 2 \u003d 0,15 o C

Na stražnjoj strani skale drugog termometra nalazi se tehnička specifikacija i naznačeno je da je za točna mjerenja potrebno uroniti termometar cijelim stražnjim dijelom. nije specificirano. Jedina preostala greška je greška u brojanju.

Ako je podjela ljestvice ovog termometra 2 o C, tada možete mjeriti temperaturu s točnošću od 1 o C. To su granice dopuštene apsolutne pogreške mjerenja i izračuna apsolutne pogreške mjerenja.

U električnim mjernim instrumentima koristi se poseban sustav za izračunavanje točnosti.

Točnost električnih mjernih instrumenata

Za određivanje točnosti takvih uređaja koristi se vrijednost koja se naziva klasa točnosti. Za njegovu oznaku koristi se slovo "Gamma". Da biste točno odredili apsolutne i relativne pogreške mjerenja, morate znati klasu točnosti uređaja, koja je naznačena na ljestvici.

Uzmimo, na primjer, ampermetar. Njegova skala označava klasu točnosti, koja pokazuje broj 0,5. Pogodan je za mjerenja istosmjerne i izmjenične struje, odnosi se na uređaje elektromagnetskog sustava.

Ovo je prilično precizan uređaj. Ako ga usporedite sa školskim voltmetrom, možete vidjeti da ima klasu točnosti 4. Ova vrijednost mora biti poznata za daljnje izračune.

Primjena znanja

Dakle, D c \u003d c (max) X γ / 100

Ova formula će se koristiti za specifične primjere. Upotrijebimo voltmetar i pronađimo grešku u mjerenju napona koji daje baterija.

Spojimo bateriju izravno na voltmetar, prethodno provjerivši je li strelica na nuli. Kada je uređaj bio spojen, strelica je odstupila za 4,2 odjeljka. Ovo se stanje može opisati na sljedeći način:

Može se vidjeti da je najveća vrijednost U za ovu stavku 6.
Razred točnosti -(γ) = 4.
U(o) = 4,2 V.
C=0,2 V

Pomoću ovih podataka formule, apsolutne i relativne pogreške mjerenja izračunavaju se na sljedeći način:

D U \u003d DU (npr.) + C / 2

D U (pr.) \u003d U (maks.) X γ / 100

D U (pr.) \u003d 6 V X 4/100 \u003d 0,24 V

Ovo je greška uređaja.

Izračun apsolutne pogreške mjerenja u ovom slučaju će se izvesti na sljedeći način:

D U = 0,24 V + 0,1 V = 0,34 V

Koristeći razmatranu formulu, lako možete saznati kako izračunati apsolutnu pogrešku mjerenja.

Postoji pravilo za pogreške zaokruživanja. Omogućuje vam da pronađete prosjek između granice apsolutne pogreške i relativne pogreške.

Učenje određivanja pogreške vaganja

Ovo je jedan primjer izravnih mjerenja. Na posebnom mjestu je vaganje. Uostalom, polužne vage nemaju vagu. Naučimo kako odrediti pogrešku takvog procesa. Na točnost mjerenja mase utječe točnost utega i savršenost same vage.

Koristimo vagu s utezima koji moraju biti postavljeni točno na desnu stranu vage. Uzmite ravnalo za vaganje.

Prije početka eksperimenta potrebno je uravnotežiti vagu. Stavili smo ravnalo na lijevu posudu.

Masa će biti jednaka zbroju ugrađenih utega. Odredimo pogrešku mjerenja ove veličine.

D m = D m (težine) + D m (težine)

Pogreška mjerenja mase sastoji se od dva člana povezana s vagom i utezima. Da biste saznali svaku od ovih vrijednosti, u tvornicama za proizvodnju vaga i utega, proizvodi se isporučuju s posebnim dokumentima koji vam omogućuju izračunavanje točnosti.

Primjena tablica

Koristimo standardnu tablicu. Greška vage ovisi o tome kolika je masa stavljena na vagu. Što je veća, veća je i pogreška.

Čak i ako stavite vrlo lagano tijelo, doći će do pogreške. To je zbog procesa trenja koji se javlja u osovinama.

Druga tablica odnosi se na skup utega. To pokazuje da svaki od njih ima svoju grešku mase. 10-gramski ima pogrešku od 1 mg, kao i 20-gramski. Izračunavamo zbroj pogrešaka svakog od ovih utega, uzetih iz tablice.

Masu i pogrešku mase zgodno je napisati u dva retka, koji se nalaze jedan ispod drugog. Što je težina manja, mjerenje je točnije.

Rezultati

Tijekom razmatranog materijala utvrđeno je da je nemoguće utvrditi apsolutnu pogrešku. Možete postaviti samo njegove granične indikatore. Za to se koriste formule opisane gore u izračunima. Ovaj materijal predloženo za proučavanje u školi za učenike od 8-9 razreda. Na temelju stečenog znanja moguće je rješavati probleme određivanja apsolutne i relativne pogreške.

U ovoj ću temi napisati nešto poput kratke varalice o pogreškama. Ponavljam, ovaj tekst nipošto nije službeni i nedopustivo je pozivati se na njega. Bio bih zahvalan za ispravak svih grešaka i netočnosti koje mogu biti u ovom tekstu.
Što je greška?
Zapisivanje rezultata pokusa oblika () znači da ako provedemo puno identičnih pokusa, tada će u 70% rezultata biti u intervalu, a u 30% neće.
Ili, što je isto, ako ponovimo eksperiment, tada će novi rezultat pasti unutar intervala pouzdanosti s vjerojatnošću jednakom vjerojatnosti povjerenja.
Kako zaokružiti grešku i rezultat?
Greška je zaokružena do prve značajne znamenke ako nije jedinica. Ako jedan, onda do dva. pri čemu značajna brojka poziva se bilo koja znamenka rezultata osim vodećih nula.
Zaokruži na ili ili ali ni pod koju cijenu, ni u kom slučaju ili , budući da postoje 2 značajne znamenke - 2 i 0 nakon dvojke.
okrugli na ili
okrugli na ili ili
Rezultat se zaokružuje tako da posljednji značajna brojka rezultat je odgovarao posljednjoj značajnoj brojki pogreške.
Primjeri ispravan zapis:
mm
Mm Ovdje u pogrešci držimo 2 značajne znamenke jer je prva značajna znamenka u pogrešci jedan.
mm
Primjeri pogrešan unos:
Mm. Ovdje dodatni znak u rezultatu. mm bilo bi točno.
mm. Ovdje dodatni znak i u pogrešci i kao rezultat. mm bilo bi točno.
U svom radu koristim vrijednost koja mi je dana jednostavno kao broj. Na primjer, masa utega. Koja je njena greška?

Ako pogreška nije izričito naznačena, možete uzeti jedinicu u zadnjoj znamenki. Odnosno, ako je napisano m = 1,35 g, tada se kao greška treba uzeti 0,01 g.
Postoji funkcija od nekoliko vrijednosti. Svaka od tih vrijednosti ima svoju grešku. Da biste pronašli pogrešku funkcije, učinite sljedeće:
Simbol označava parcijalnu derivaciju f u odnosu na x. Pročitajte više o parcijalnim izvedenicama.
Pretpostavimo da ste izmjerili istu vrijednost x nekoliko (n) puta. Dobio skup vrijednosti. . Morate izračunati pogrešku širenja, izračunati instrumentalnu pogrešku i zbrojiti ih.
Bodovi.
1. Izračunajte pogrešku širenja
Ako se sve vrijednosti poklapaju, nema rasipanja. U suprotnom, postoji pogreška raspršenja koja se mora izračunati. Za početak, izračunava se korijen srednje kvadratne pogreške srednje vrijednosti:
Ovdje znači prosjek u odnosu na sve.
Pogreška raspršenja dobiva se množenjem efektivne pogreške srednje vrijednosti sa Studentovim koeficijentom, koji ovisi o razini pouzdanosti koju odaberete i broju mjerenja n:
Studentski koeficijenti preuzeti su iz donje tablice. Razina pouzdanosti je slučajno odabrana, broj mjerenja n također znamo.
2. Razmatramo instrumentalnu pogrešku srednje vrijednosti
Ako su pogreške različitih točaka različite, onda prema formuli
U ovom slučaju, naravno, sva vjerojatnost povjerenja trebala bi biti ista.
3. Zbrojite prosjek s namazom
Pogreške se uvijek zbrajaju kao korijen iz kvadrata:
U tom slučaju morate biti sigurni da se vjerojatnosti pouzdanosti s kojima su izračunate i podudaraju.

Kako odrediti instrumentalnu pogrešku sredine s grafa? Pa, to jest, koristeći metodu uparenih točaka ili metodu najmanjih kvadrata, nalazimo pogrešku u širenju prosječnog otpora. Kako pronaći instrumentalnu pogrešku prosječnog otpora?
I u LSM-u iu metodi uparenih točaka moguće je dati rigorozan odgovor na ovo pitanje. Za MNC forum u Svetozarovu postoji ("Osnove ...", odjeljak o metodi najmanjih kvadrata), a za uparene točke prvo što pada na pamet (na čelo, što se kaže) je izračunati instrumentalna greška svakog nagiba. Pa, na sve točke...
Ako ne želite patiti, onda u Labsu postoji jednostavan način za to procjene instrumentalna pogreška kutnog koeficijenta, naime iz LSM-a sljedeće (na primjer, prije rada 1 u laboratoriju "Električni mjerni instrumenti. ..." zadnja stranica Metoda.preporuke).
Gdje je vrijednost najvećeg odstupanja po osi Y točke s pogreškom od nacrtane ravne linije, a nazivnik je širina površine našeg grafikona po osi Y. Slično i po osi X.

Na spremniku otpora klasa točnosti je napisana: 0,05 / 4 * 10 ^-6? Kako pronaći grešku uređaja iz ovoga?
To znači da granična relativna pogreška uređaja (u postocima) ima oblik:
, Gdje
- najveća vrijednost otpor pohranjivanja, i - nominalna vrijednost uključenog otpora.
Lako je vidjeti da je drugi član važan kada radimo na vrlo niskim otporima.
Više detalja uvijek možete pronaći u putovnici uređaja. Putovnicu možete pronaći na internetu tako da u Google unesete marku uređaja.
Literatura o pogreškama
Puno više informacija o ovoj temi možete pronaći u knjizi preporučenoj za studente prve godine:
V.V. Svetozarov "Elementarna obrada rezultata mjerenja"
Kao dodatnu (za studente prve godine dodatnu) literaturu možemo preporučiti:
V.V. Svetozarov "Osnove statističke obrade rezultata mjerenja"
A za one koji žele konačno sve shvatiti, svakako pogledajte ovdje:
J. Taylor. "Uvod u teoriju pogrešaka"
Hvala vam što ste pronašli i objavili ove prekrasne knjige na svojoj stranici.

Pri mjerenju bilo koje količine uvijek postoji neko odstupanje od prave vrijednosti, od činjenice da nijedan instrument ne može dati točan rezultat. Kako bi se utvrdilo tolerancije dobivenih podataka iz točne vrijednosti koriste se prikazi relativne i bezuvjetne pogreške.

Trebat će vam

– rezultate mjerenja;
- kalkulator.

Uputa

1. Prije svega napravite nekoliko mjerenja uređajem iste vrijednosti kako biste mogli izračunati stvarnu vrijednost. Što su veća mjerenja, rezultat će biti točniji. Recimo, izvažite jabuku na elektronskoj vagi. Moguće je da ste dobili ukupno 0,106, 0,111, 0,098 kg.

2. Sada izračunajte stvarnu vrijednost vrijednosti (važeću, iz činjenice da je nerealno otkriti istinu). Da biste to učinili, zbrojite rezultate i podijelite ih s brojem mjerenja, odnosno pronađite aritmetičku sredinu. U primjeru bi stvarna vrijednost bila (0,106+0,111+0,098)/3=0,105.

3. Za izračun bezuvjetne pogreške prvog mjerenja oduzmite stvarnu vrijednost od ukupne vrijednosti: 0,106-0,105=0,001. Na isti način izračunajte bezuvjetne pogreške preostalih mjerenja. Imajte na umu da bez obzira na to je li rezultat minus ili plus, predznak pogreške uvijek je pozitivan (to jest, uzimate modul vrijednosti).

4. Da biste dobili relativnu pogrešku prvog mjerenja, podijelite bezuvjetnu pogrešku sa stvarnom vrijednošću: 0,001/0,105=0,0095. Imajte na umu da se relativna pogreška obično mjeri kao postotak, stoga pomnožite dobiveni broj sa 100%: 0,0095x100% \u003d 0,95%. Na isti način razmotrite relativne pogreške preostalih mjerenja.

5. Ako je prava vrijednost bolje poznata, odmah prijeđite na izračun pogrešaka, isključujući traženje aritmetičke sredine rezultata mjerenja. Odmah oduzmite ukupni iznos od prave vrijednosti i pronaći ćete bezuvjetnu pogrešku.

6. Nakon toga podijelite bezuvjetnu pogrešku sa stvarnom vrijednošću i pomnožite sa 100% - to će biti relativna pogreška. Recimo da je broj učenika 197, ali je zaokružen na 200. U ovom slučaju izračunajte pogrešku zaokruživanja: 197-200=3, relativnu pogrešku: 3/197x100%=1,5%.

Greška je vrijednost koja određuje dopuštena odstupanja primljenih podataka od točne vrijednosti. Postoje prikazi relativnih i bezuvjetnih pogrešaka. Njihovo pronalaženje jedan je od zadataka matematičke smotre. Međutim, u praksi je značajnije izračunati pogrešku širenja nekog mjerenog pokazatelja. Fizički instrumenti imaju vlastitu moguću grešku. Ali ne samo da se to mora uzeti u obzir pri određivanju pokazatelja. Da bi se izračunala pogreška širenja σ, potrebno je provesti nekoliko mjerenja ove veličine.

Trebat će vam

Uređaj za mjerenje tražene vrijednosti

Uputa

1. Izmjerite uređajem ili drugim mjernim alatom vrijednost koja vam je potrebna. Ponovite mjerenja nekoliko puta. Što su veće dobivene vrijednosti, veća je točnost određivanja pogreške širenja. Tradicionalno se provodi 6-10 mjerenja. Zapišite dobiveni skup vrijednosti izmjerene veličine.

2. Ako su sve dobivene vrijednosti jednake, pogreška širenja je nula. Ako postoje različite vrijednosti u seriji, izračunajte pogrešku širenja. Da biste ga odredili, postoji posebna formula.

3. Prema formuli prvo izračunajte prosječnu vrijednost<х>od primljenih vrijednosti. Da biste to učinili, zbrojite sve vrijednosti i podijelite njihov zbroj s brojem mjerenja n.

4. Redom odredite razliku između ukupne dobivene vrijednosti i prosječne vrijednosti<х>. Zapišite zbrojeve dobivenih razlika. Zatim kvadrirajte sve razlike. Nađi zbroj zadanih kvadrata. Sačuvajte konačni primljeni iznos.

5. Izračunajte izraz n(n-1), gdje je n broj mjerenja koja ste izvršili. Zbroj zbroja iz prethodnog izračuna podijelite s dobivenom vrijednošću.

6. Izvadite kvadratni korijen dijeljenja. To će biti pogreška u širenju σ, vrijednosti koju ste izmjerili.

Prilikom izvođenja mjerenja nemoguće je jamčiti njihovu točnost, svaki uređaj daje određeno greška. Da bi se saznala točnost mjerenja ili klasa točnosti uređaja, potrebno je odrediti bezuvjetnu i relativnu greška .

Trebat će vam

– više rezultata mjerenja ili drugi uzorak;
- kalkulator.

Uputa

1. Izvršite mjerenja najmanje 3-5 puta kako biste mogli izračunati stvarnu vrijednost parametra. Rezultate zbrojite i podijelite s brojem mjerenja, dobijete stvarnu vrijednost, koja se koristi u zadacima umjesto istinite (nerealno ju je odrediti). Recimo ako su mjerenja dala ukupno 8, 9, 8, 7, 10, tada će stvarna vrijednost biti (8+9+8+7+10)/5=8,4.

2. Otkrij bezuvjetno greška cijelo mjerenje. Da biste to učinili, oduzmite stvarnu vrijednost od rezultata mjerenja, zanemarite znakove. Dobit ćete 5 bezuvjetnih pogrešaka, jednu za svako mjerenje. U primjeru će biti jednaki 8-8,4 = 0,4, 9-8,4 = 0,6, 8-8,4 = 0,4, 7-8,4 = 1,4, 10-8,4 = 1,6 (uzimaju se moduli rezultata).

3. Da saznam rodbinu greška bilo koje dimenzije, podijelite bezuvjetno greška na stvarnu (pravu) vrijednost. Nakon toga pomnožite rezultat sa 100%, tradicionalno se ova vrijednost mjeri u postocima. U primjeru otkrijte relativnu greška prema tome: ?1=0,4/8,4=0,048 (ili 4,8%), ?2=0,6/8,4=0,071 (ili 7,1%), ?3=0,4/ 8,4=0,048 (ili 4,8%), ?4=1,4/8,4 =0,167 (ili 16,7%), ?5=1,6/8,4=0,19 (ili 19%).

4. U praksi se za posebno točan prikaz pogreške koristi standardna devijacija. Da biste ga pronašli, kvadrirajte sve bezuvjetne pogreške mjerenja i zbrojite ih. Zatim podijelite ovaj broj s (N-1), gdje je N broj mjerenja. Izračunavanjem korijena dobivenog ukupnog iznosa dobit ćete karakteristiku standardne devijacije greška mjerenja.

5. Kako bismo otkrili krajnje bezuvjetno greška, pronađite najmanji broj za koji se zna da je veći od bezuvjetnog greška ili njemu jednaka. U razmatranom primjeru primitivno odabrati najveću vrijednost - 1,6. Također je povremeno potrebno pronaći ograničavajući relativ greška, zatim pronađite broj koji je veći ili jednak relativnoj pogrešci, u primjeru je to 19%.

Neodvojivi dio svakog mjerenja je neki greška. Predstavlja dobru ocjenu točnosti ankete. Prema obliku prikazivanja može biti bezuvjetna i relativna.

Trebat će vam

- kalkulator.

Uputa

1. Greške fizička mjerenja dijele se na sustavne, nasumične i odvažne. Prvi su uzrokovani čimbenicima koji djeluju identično kada se mjerenja ponavljaju mnogo puta. Oni su kontinuirani ili se zakonito mijenjaju. Mogu biti uzrokovani nepravilnom ugradnjom uređaja ili nesavršenošću odabrane metode mjerenja.

2. Drugi proizlaze iz moći uzroka i bezuzročne dispozicije. To uključuje netočno zaokruživanje pri brojanju iskaza i moći okoliš. Ako su takve pogreške mnogo manje od podjeljaka ljestvice ovog mjernog instrumenta, tada je prikladno kao bezuvjetnu pogrešku uzeti pola podjeljka.

3. Miss ili odvažnost greška predstavlja rezultat praćenja, koji se bitno razlikuje od svih ostalih.

4. Bezuvjetno greška približan brojčana vrijednost je razlika između rezultata dobivenog tijekom mjerenja i prave vrijednosti mjerene veličine. Prava ili stvarna vrijednost posebno točno odražava fizičku veličinu koja se proučava. Ovaj greška je najlakša kvantitativna mjera pogreške. Može se izračunati pomoću sljedeće formule: ?X = Hisl - Hist. Može imati pozitivno i negativno značenje. Za bolje razumijevanje, pogledajmo primjer. Škola ima 1205 učenika, kada se zaokruži na 1200 bezuvjetnih greška jednako: ? = 1200 - 1205 = 5.

5. postojati određena pravila izračun pogreške vrijednosti. Prvo, bezuvjetno greška zbroj 2 neovisne vrijednosti jednak je zbroju njihovih bezuvjetnih pogrešaka: ?(X+Y) = ?X+?Y. Sličan pristup primjenjiv je za razliku od 2 pogreške. Dopušteno je koristiti formulu: ?(X-Y) = ?X+?Y.

6. Amandman je bezuvjetan greška, uzet sa suprotnim predznakom: ?p = -?. Koristi se za uklanjanje sustavne pogreške.

mjerenja fizičke veličine uvijek prate jedno ili drugo greška. Predstavlja odstupanje rezultata mjerenja od prave vrijednosti izmjerene vrijednosti.

Trebat će vam

- mjerni uređaj:
-kalkulator.

Uputa

1. Pogreške se mogu pojaviti kao rezultat snage različitih čimbenika. Među njima je dopušteno istaknuti nesavršenost sredstava ili metoda mjerenja, netočnosti u njihovoj proizvodnji, nepoštivanje posebnih uvjeta tijekom istraživanja.

2. Postoji nekoliko klasifikacija grešaka. Prema obliku prikazivanja mogu biti bezuvjetni, relativni i reducirani. Prvi su razlika između izračunate i stvarne vrijednosti količine. Izražavaju se u jedinicama mjerene pojave i nalaze se formulom: x = hisl-hist. Potonji se određuju omjerom bezuvjetnih pogrešaka prema vrijednosti stvarne vrijednosti pokazatelja. Formula za izračun izgleda ovako:? = ?h/pov. Mjeri se u postocima ili udjelima.

3. Smanjena pogreška mjernog uređaja nalazi se kao omjer ?x prema normalizirajućoj vrijednosti xn. Ovisno o vrsti uređaja, uzima se ili jednako granici mjerenja ili se odnosi na njihov specifični raspon.

4. Prema uvjetima nastanka razlikuju se osnovni i dopunski. Ako su mjerenja provedena u tipičnim uvjetima, tada se pojavljuje 1. tip. Dodatna su odstupanja zbog izlaza vrijednosti izvan tipičnih granica. Da bi se to ocijenilo, dokumentacija obično utvrđuje norme unutar kojih se vrijednost može promijeniti ako se krše uvjeti mjerenja.

5. Također, pogreške fizičkih mjerenja dijele se na sustavne, slučajne i smjele. Prvi su uzrokovani čimbenicima koji djeluju nakon opetovanog ponavljanja mjerenja. Drugi proizlaze iz moći uzroka i bezuzročne dispozicije. Promašaj je rezultat praćenja, koji se drastično razlikuje od svih ostalih.

6. Ovisno o prirodi mjerene veličine, različite metode greška mjerenja. Prva od njih je Kornfeldova metoda. Temelji se na izračunu intervala pouzdanosti u rasponu od najmanjeg do najvećeg ukupnog iznosa. Pogreška će u ovom slučaju biti polovica razlike između ovih ukupnih zbrojeva: ?x = (xmax-xmin)/2. Druga metoda je izračun srednje kvadratne pogreške.

Mjerenja se mogu provesti s različitim stupnjevima točnosti. U isto vrijeme, čak ni precizni instrumenti sigurno nisu točni. Bezuvjetne i relativne pogreške mogu biti male, ali u stvarnosti su gotovo nepromijenjene. Razlika između približnih i točne vrijednosti određena vrijednost naziva se bezuvjetna greška. U ovom slučaju odstupanje može biti i veliko i malo.

Trebat će vam

– podaci mjerenja;
- kalkulator.

Uputa

1. Prije izračuna bezuvjetne pogreške uzmite nekoliko postulata kao početne podatke. Uklonite odvažne pogreške. Prihvatite da su potrebne korekcije već izračunate i dodane ukupnom iznosu. Takva korekcija može biti, recimo, prijenos početne točke mjerenja.

2. Uzmite kao početnu lokaciju ono što je poznato i slučajne pogreške se uzimaju u obzir. To implicira da su oni manje sustavni, odnosno bezuvjetni i relativni, karakteristični za ovaj uređaj.

3. Slučajne pogreške utječu na rezultat čak i vrlo preciznih mjerenja. Posljedično, svaki će rezultat biti više-manje blizak bezuvjetnom, ali će uvijek postojati odstupanja. Definirajte ovaj interval. Može se izraziti formulom (Xism-?X)?Chism? (Hizm+?X).

4. Odredite vrijednost koja je najbliža pravoj vrijednosti. U stvarnim mjerenjima uzima se aritmetička sredina koja se može pronaći pomoću formule prikazane na slici. Ukupno uzmite kao pravu vrijednost. U mnogim slučajevima očitanje referentnog instrumenta smatra se točnim.

5. Znajući pravu vrijednost mjerenja, možete pronaći apsolutnu pogrešku, koja se mora uzeti u obzir u svim sljedećim mjerenjima. Otkrij x1 vrijednost - podatak određena dimenzija. Odredite razliku?X, oduzimajući od više manji. Pri određivanju pogreške uzima se u obzir samo modul te razlike.

Bilješka!
Kao i obično, u praksi je nemoguće provesti bezuvjetno točno mjerenje. Posljedično, granična pogreška se uzima kao referentna vrijednost. Ona predstavlja najveća vrijednost modul bezuvjetne pogreške.

Koristan savjet
U utilitarističkim mjerenjima vrijednost bezuvjetne pogreške obično se uzima kao polovica najniža cijena podjela. Kod rada s brojevima, bezuvjetna pogreška se uzima kao polovica vrijednosti znamenke, koja je u sljedećoj kategoriji iza točnih znamenki. Za određivanje klase točnosti uređaja glavna stvar je omjer bezuvjetne pogreške prema rezultatu mjerenja ili prema duljini ljestvice.

Pogreške mjerenja povezane su s nesavršenošću instrumenata, alata, metodologije. Točnost također ovisi o promatranju i stanju eksperimentatora. Pogreške se dijele na bezuvjetne, relativne i reducirane.

Uputa

1. Neka jedno mjerenje vrijednosti da ukupni x. Prava vrijednost je označena sa x0. Zatim bezuvjetno greška?x=|x-x0|. Procjenjuje bezuvjetnu grešku mjerenja. Bezuvjetno greška sastoji se od 3 komponente: slučajne pogreške, sustavne pogreške i promašaji. Obično se kod mjerenja instrumentom kao pogreška uzima polovica vrijednosti podjele. Za milimetarsko ravnalo to bi bilo 0,5 mm.

2. Prava vrijednost izmjerene vrijednosti je u intervalu (x-?x; x+?x). Ukratko, ovo se piše kao x0=x±?x. Glavno je mjeriti x i ?x u istim mjernim jedinicama i pisati brojeve u istom formatu, recimo, cijeli broj i tri znamenke iza decimalne točke. Ispada, bezuvjetno greška daje granice intervala u kojem se s nekom vjerojatnošću nalazi prava vrijednost.

3. Relativni greška izražava omjer bezuvjetne pogreške prema stvarnoj vrijednosti veličine: ?(x)=?x/x0. Ovo je bezdimenzijska veličina, može se napisati i kao postotak.

4. Mjerenja su izravna ili neizravna. Kod izravnih mjerenja željena vrijednost se odmah mjeri odgovarajućim instrumentom. Recimo, duljina tijela mjeri se ravnalom, napon se mjeri voltmetrom. Kod neizravnih mjerenja vrijednost se nalazi prema formuli odnosa između nje i izmjerenih vrijednosti.

5. Ako je rezultat veza 3 lako mjerljive veličine s pogreškama ?x1, ?x2, ?x3, tada greška neizravno mjerenje?F=?[(?x1 ?F/?x1)?+(?x2 ?F/?x2)?+(?x3 ?F/?x3)?]. Ovdje?F/?x(i) su parcijalne derivacije funkcije u odnosu na bilo koju od slobodno mjerljivih veličina.

Koristan savjet
Promašaji su drske netočnosti mjerenja koje nastaju neispravnim radom instrumenata, nepažnjom eksperimentatora i kršenjem eksperimentalne metodologije. Kako biste smanjili vjerojatnost takvih promašaja, budite oprezni prilikom mjerenja i detaljno opišite rezultat.

Rezultat svakog mjerenja neizbježno prati odstupanje od prave vrijednosti. Pogrešku mjerenja moguće je izračunati na više metoda, ovisno o njezinoj vrsti, npr. statističkim metodama za određivanje intervala pouzdanosti, standardne devijacije itd.

Uputa

1. Nekoliko je razloga za to pogreške mjerenja. To su instrumentalne netočnosti, nesavršenost metodologije, kao i pogreške uzrokovane nepažnjom operatera koji provodi mjerenja. Osim toga, često se kao stvarna vrijednost parametra uzima njegova stvarna vrijednost, što je zapravo jedino moguće na temelju pregleda statističkog uzorka rezultata niza eksperimenata.

2. Pogreška je mjera odstupanja mjerenog parametra od njegove prave vrijednosti. Kornfeldovom metodom određuje se interval povjerenja koji jamči određeni stupanj sigurnosti. Istodobno se pronalaze takozvane granice pouzdanosti, u kojima vrijednost varira, a pogreška se izračunava kao poluzbroj tih vrijednosti:? = (xmax – xmin)/2.

3. Ovo je procjena intervala. pogreške, što ima smisla provesti s malom količinom statističkog uzorkovanja. Točkasta procjena sastoji se od izračuna matematičkog očekivanja i standardne devijacije.

4. Očekivana vrijednost je integralni zbroj niza proizvoda 2 parametra praćenja. To su zapravo vrijednosti mjerene veličine i njezine vjerojatnosti u ovim točkama: M = ?xi pi.

5. Klasična formula za izračunavanje standardne devijacije pretpostavlja izračun prosječne vrijednosti analiziranog niza vrijednosti izmjerene vrijednosti, a također uzima u obzir volumen niza izvedenih eksperimenata: = ?(?(xi – xav)?/(n – 1)).

6. Prema načinu izražavanja razlikuju se i bezuvjetne, relativne i reducirane pogreške. Bezuvjetna pogreška izražava se u istim jedinicama kao i izmjerena vrijednost, a jednaka je razlici između njezine izračunate i prave vrijednosti: x = x1 - x0.

7. Relativna mjerna pogreška povezana je s bezuvjetnom, ali je učinkovitija. Nema dimenziju, ponekad se izražava u postotku. Njegova vrijednost jednaka je omjeru bezuvjetnog pogreške na pravu ili izračunatu vrijednost mjerenog parametra:?x = ?x/x0 ili?x = ?x/x1.

8. Smanjena pogreška se izražava kao omjer između bezuvjetne pogreške i neke konvencionalno prihvaćene vrijednosti x, koja je konstantna za sve mjerenja a određuje se stupnjevanjem skale instrumenta. Ako ljestvica počinje od nule (jednostrana), tada je ta normalizirajuća vrijednost jednaka njezinoj gornjoj granici, a ako je dvostrana, širina svakog od njezinih raspona:? = ?x/xn.

Samoupravljanje dijabetesom smatra se važnom komponentom liječenja. Glukometar se koristi za mjerenje šećera u krvi kod kuće. Moguća pogreška ovog uređaja je veća nego kod laboratorijskih analizatora glikemije.

Mjerenje šećera u krvi potrebno je za procjenu učinkovitosti liječenja dijabetesa i prilagođavanje doze lijekova. O propisanoj terapiji ovisi koliko puta mjesečno trebate mjeriti šećer. Povremeno je potrebno više puta tijekom dana uzeti uzorke krvi za pregled, povremeno 1-2 puta tjedno. Samokontrola je potrebna isključivo trudnicama i oboljelima od dijabetesa tipa 1.

Dopuštena pogreška za glukometar prema međunarodnim standardima

Glukometar se ne smatra preciznim instrumentom. Priprema se samo za približno određivanje koncentracije šećera u krvi. Moguća pogreška glukometra prema svjetskim standardima je 20% s glikemijom većom od 4,2 mmol / l. Na primjer, ako je tijekom samokontrole fiksirana razina šećera od 5 mmol/l, tada je stvarna vrijednost koncentracije u rasponu od 4 do 6 mmol/l. Moguća pogreška glukometra u standardnim uvjetima mjeri se u postotku, a ne u mmol / l. Što su pokazatelji veći, to je veća pogreška u bezuvjetnim brojevima. Recimo, ako šećer u krvi dosegne oko 10 mmol/l, tada pogreška ne prelazi 2 mmol/l, a ako je šećer oko 20 mmol/l, tada je razlika s ukupnim laboratorijsko mjerenje može biti do 4 mmol / l. U većini slučajeva glukometar precjenjuje glikemiju.Standardi dopuštaju prekoračenje navedene pogreške mjerenja u 5% slučajeva. To znači da svako dvadeseto istraživanje može značajno iskriviti rezultate.

Dopuštena pogreška za glucometre različitih tvrtki

Glukometri podliježu obveznom certificiranju. Dokumenti koji prate uređaj obično pokazuju brojke za moguću grešku mjerenja. Ako ove stavke nema u uputama, tada pogreška odgovara 20%. Neki proizvođači brojila poseban naglasak stavljaju na točnost mjerenja. Postoje uređaji europskih tvrtki koji imaju moguću grešku manju od 20%. Najbolji pokazatelj danas je 10-15%.

Pogreška glukometra tijekom samokontrole

Dopuštena pogreška mjerenja karakterizira rad uređaja. Nekoliko drugih čimbenika također utječe na točnost ankete. Nenormalno pripremljena koža, premala ili prevelika primljena kap krvi, neprihvatljivo temperaturni režim- sve to može dovesti do grešaka. Samo ako se poštuju sva pravila samokontrole, dopušteno je osloniti se na deklariranu moguću pogrešku ankete. Pravila samokontrole uz pomoć glukometra možete dobiti od ordinirajućeg liječnika, a točnost glukometra možete provjeriti u servisni centar. Jamstva proizvođača uključuju besplatne konzultacije i rješavanje problema.