Propagation of vibrations in a medium. Waves
OK-9 Propagation of vibrations in an elastic medium
Wave motion- mechanical waves, i.e. waves that propagate only in matter (sea, sound, waves in a string, earthquake waves). The sources of the waves are vibrations of the vibrator.
Vibrator- oscillating body. Creates vibrations in an elastic medium.
Wave are called vibrations that propagate in space over time.
wave surface- geometric locus of points in the medium oscillating in the same phases
L  uch- a line whose tangent at each point coincides with the direction of propagation of the wave.
uch- a line whose tangent at each point coincides with the direction of propagation of the wave.
The reason for the occurrence of waves in an elastic medium
If a vibrator vibrates in an elastic medium, then it acts on the particles of the medium, causing them to perform forced vibrations. Due to the interaction forces between particles of the medium, vibrations are transmitted from one particle to another.
T  wave types
wave types
Transverse waves
Waves in which vibrations of particles of the medium occur in a plane perpendicular to the direction of propagation of the wave. Occur in solids and on the surface of the hearth.
P  maternity waves
maternity waves
Oscillations occur along the propagation of the wave. Can occur in gases, liquids and solids.
Surface waves
IN  waves that propagate at the interface between two media. Waves at the boundary between water and air. If λ
is less than the depth of the reservoir, then each particle of water on the surface and near it moves along an ellipse, i.e. is a combination of vibrations in the longitudinal and transverse directions. At the bottom, purely longitudinal movement is observed.
waves that propagate at the interface between two media. Waves at the boundary between water and air. If λ
is less than the depth of the reservoir, then each particle of water on the surface and near it moves along an ellipse, i.e. is a combination of vibrations in the longitudinal and transverse directions. At the bottom, purely longitudinal movement is observed.
Plane waves
Waves in which the wave surfaces are planes perpendicular to the direction of wave propagation.
WITH  spherical waves
spherical waves
Waves whose wave surfaces are spheres. The spheres of the wave surfaces are concentric.
Characteristics of wave motion


Wavelength
The shortest distance between two races oscillating in the same phase is called wavelength. Depends only on the medium in which the wave propagates, at equal vibrator frequencies.
Frequency
Frequency ν wave motion depends only on the frequency of the vibrator.
Wave propagation speed
Speed v= λν
. Because  , That
, That  . However, the speed of wave propagation depends on the type of substance and its state; from ν
And λ
, does not depend.
. However, the speed of wave propagation depends on the type of substance and its state; from ν
And λ
, does not depend.
In an ideal gas  , Where R- gas constant; M- molar mass; T- absolute temperature; γ
- constant for a given gas; ρ
- density of the substance.
, Where R- gas constant; M- molar mass; T- absolute temperature; γ
- constant for a given gas; ρ
- density of the substance.
Transverse waves in solids  , Where N- shear modulus; longitudinal waves
, Where N- shear modulus; longitudinal waves  , Where Q- all-round compression module. In solid rods
, Where Q- all-round compression module. In solid rods  Where E- Young's modulus.
Where E- Young's modulus.
In solids, both transverse and longitudinal waves propagate at different speeds. This is the basis for determining the epicenter of an earthquake.
Plane wave equation
His appearance x=x 0 sin ωt(t−l/v) = x 0 sin( ωt−kl), Where k= 2π /λ - wave number; l- the distance traveled by the wave from the vibrator to the point in question A.
Time delay of oscillations of points in the medium:  .
.
Phase delay of oscillations of points in the medium:  .
.
Phase difference between two oscillating points: ∆ φ =φ 2 −φ 1 = 2π (l 2 −l 1)/λ .
Wave energy
Waves transfer energy from one vibrating particle to another. The particles perform only oscillatory movements, but do not move with the wave: E=E k + E P,
Where E k is the kinetic energy of an oscillating particle; E n is the potential energy of elastic deformation of the medium.
To some extent V elastic medium in which a wave with amplitude propagates X 0 and cyclic frequency ω
, there is an average energy W, equal  , Where m- mass of the allocated volume of the medium.
, Where m- mass of the allocated volume of the medium.
Wave intensity
A physical quantity that is equal to the energy transferred by a wave per unit time through a unit surface area perpendicular to the direction of propagation of the wave is called wave intensity:  . It is known that W And j~
. It is known that W And j~ .
.
Wave power
If S is the transverse surface area through which energy is transferred by the wave, and j- wave intensity, then the wave power is equal to: p=jS.
OK-10 Sound waves
U  Spring waves that cause a person to experience sound are called sound waves.
Spring waves that cause a person to experience sound are called sound waves.
16 –2∙10 4 Hz - audible sounds;
less than 16 Hz - infrasounds;
more than 2∙10 4 Hz - ultrasounds.
ABOUT  A prerequisite for the occurrence of a sound wave is the presence of an elastic medium.
A prerequisite for the occurrence of a sound wave is the presence of an elastic medium.
M  The mechanism for the generation of a sound wave is similar to the generation of a mechanical wave in an elastic medium. Vibrating in an elastic medium, the vibrator affects the particles of the medium.
The mechanism for the generation of a sound wave is similar to the generation of a mechanical wave in an elastic medium. Vibrating in an elastic medium, the vibrator affects the particles of the medium.
Sound is created by long-term periodic sound sources. For example, musical: string, tuning fork, whistling, singing.
Noise is created by long-term, but not periodic sound sources: rain, sea, crowd.
Sound speed
Depends on the medium and its state, as for any mechanical wave:
 .
.
At t= 0°C water v = 1430 m/s, steel v = 5000 m/s, air v = 331 m/s.
Sound wave receivers
1. Artificial: the microphone converts mechanical sound vibrations into electrical ones. Characterized by sensitivity σ
: ,σ
depends on ν
z.v. .
,σ
depends on ν
z.v. .
2. Natural: ear.
Its sensitivity perceives sound at ∆ p= 10 −6 Pa.
The lower the frequency ν sound wave, the less sensitivity σ ear. If ν z.v. decreases from 1000 to 100 Hz, then σ ear is reduced by 1000 times.
Exceptional selectivity: the conductor captures the sounds of individual instruments.
Physical characteristics of sound
Objective
1. Sound pressure is the pressure exerted by a sound wave on an obstacle in front of it.
2. The sound spectrum is the decomposition of a complex sound wave into its component frequencies.

3.
Intensity sound wave:  , Where S- surface area; W- sound wave energy; t- time;
, Where S- surface area; W- sound wave energy; t- time;  .
.
Subjective
Volume, like height, sound is associated with the sensation that arises in the human mind, as well as with the intensity of the wave.
The human ear is capable of perceiving sounds with intensities from 10 −12 (audibility threshold) to 1  (pain threshold).
(pain threshold).
G 
 Loudness is not directly proportional to intensity. To get a sound 2 times louder, you need to increase the intensity 10 times. A wave with an intensity of 10 −2 W/m 2 sounds 4 times louder than a wave with an intensity of 10 −4 W/m 2 . Because of this relationship between the objective sensation of loudness and sound intensity, a logarithmic scale is used.
Loudness is not directly proportional to intensity. To get a sound 2 times louder, you need to increase the intensity 10 times. A wave with an intensity of 10 −2 W/m 2 sounds 4 times louder than a wave with an intensity of 10 −4 W/m 2 . Because of this relationship between the objective sensation of loudness and sound intensity, a logarithmic scale is used.
The unit of this scale is the bel (B) or decibel (dB), (1 dB = 0.1 B), named after the physicist Heinrich Behl. The volume level is expressed in bels:  , Where I 0 = 10 −12
, Where I 0 = 10 −12  hearing threshold (average).
hearing threshold (average).
E  if I= 10 −2
if I= 10 −2  , That
, That  .
.
Loud sounds are harmful to our body. The sanitary standard is 30–40 dB. This is the volume of a calm, quiet conversation.
Noise disease: high blood pressure, nervous excitability, hearing loss, fatigue, poor sleep.
Intensity and volume of sound from various sources: jet aircraft - 140 dB, 100 W/m2; rock music indoors - 120 dB, 1 W/m2; normal conversation (50 cm from it) - 65 dB, 3.2∙10 −6 W/m 2.
Pitch depends on the oscillation frequency: than > ν , the higher the sound.
T  sound timbre allows you to distinguish between two sounds of the same pitch and volume produced by different instruments. It depends on the spectral composition.
sound timbre allows you to distinguish between two sounds of the same pitch and volume produced by different instruments. It depends on the spectral composition.
Ultrasound
Applicable: echo sounder for determining the depth of the sea, preparing emulsions (water, oil), washing parts, tanning leather, detecting defects in metal products, in medicine, etc.
Distributes over considerable distances in solids and liquids. Transfers energy much greater than a sound wave.
Let the oscillating body be in a medium in which all the particles are interconnected. The particles of the medium in contact with it will begin to vibrate, as a result of which periodic deformations (for example, compression and tension) occur in the areas of the medium adjacent to this body. During deformations, elastic forces appear in the medium, which tend to return the particles of the medium to their original state of equilibrium.
Thus, periodic deformations that appear in some place in an elastic medium will propagate at a certain speed, depending on the properties of the medium. In this case, the particles of the medium are not drawn into translational motion by the wave, but perform oscillatory movements around their equilibrium positions; only elastic deformation is transferred from one part of the medium to another.
The process of propagation of oscillatory motion in a medium is called wave process or simply wave. Sometimes this wave is called elastic, because it is caused by the elastic properties of the medium.
Depending on the direction of particle oscillations relative to the direction of wave propagation, longitudinal and transverse waves are distinguished.Interactive demonstration of transverse and longitudinal waves

Longitudinal wave –
This is a wave in which particles of the medium oscillate along the direction of propagation of the wave.

A longitudinal wave can be observed on a long soft spring large diameter. By hitting one of the ends of the spring, you can notice how successive condensations and rarefactions of its turns will spread throughout the spring, running one after another. In the figure, the dots show the position of the spring coils at rest, and then the positions of the spring coils at successive time intervals equal to a quarter of the period.

Demonstration of longitudinal wave propagation
Transverse wave -
This is a wave in which the particles of the medium oscillate in directions perpendicular to the direction of propagation of the wave.

Let us consider in more detail the process of formation of transverse waves. Let us take as a model of a real cord a chain of balls (material points) connected to each other by elastic forces. The figure depicts the process of propagation of a transverse wave and shows the positions of the balls at successive time intervals equal to a quarter of the period.

At the initial moment of time (t 0 = 0) all points are in a state of equilibrium. Then we cause a disturbance by deviating point 1 from the equilibrium position by an amount A and the 1st point begins to oscillate, the 2nd point, elastically connected to the 1st, comes into oscillatory motion a little later, the 3rd even later, etc. . After a quarter of the oscillation period ( t 2 = T 4 ) will spread to the 4th point, the 1st point will have time to deviate from its equilibrium position by maximum distance, equal to the amplitude of oscillations A. After half a period, the 1st point, moving downwards, will return to the equilibrium position, the 4th deviated from the equilibrium position by a distance equal to the amplitude of oscillations A, the wave has spread to the 7th point, etc.
By the time t 5 = T The 1st point, having completed a complete oscillation, passes through the equilibrium position, and the oscillatory movement will spread to the 13th point. All points from the 1st to the 13th are located so that they form a complete wave consisting of depressions And ridge
Demonstration of shear wave propagation
The type of wave depends on the type of deformation of the medium. Longitudinal waves are caused by compression-tension deformation, transverse waves are caused by shear deformation. Therefore, in gases and liquids, in which elastic forces arise only during compression, the propagation of transverse waves is impossible. In solids, elastic forces arise both during compression (tension) and shear, therefore, both longitudinal and transverse waves can propagate in them.
As the figures show, in both transverse and longitudinal waves, each point of the medium oscillates around its equilibrium position and shifts from it by no more than an amplitude, and the state of deformation of the medium is transferred from one point of the medium to another. An important difference between elastic waves in a medium and any other ordered movement of its particles is that the propagation of waves is not associated with the transfer of matter in the medium.
Consequently, when waves propagate, energy of elastic deformation and momentum are transferred without transfer of matter. The energy of a wave in an elastic medium consists of the kinetic energy of oscillating particles and the potential energy of elastic deformation of the medium.

Repeated movements or changes in state are called oscillations (alternating electric current, the movement of a pendulum, the work of the heart, etc.). All vibrations, regardless of their nature, have some general principles. Oscillations propagate in the medium in the form of waves. This chapter discusses mechanical vibrations and waves.
7.1. HARMONIC VIBRATIONS
Among various types vibrations the simplest form is harmonic oscillation those. one in which the oscillating quantity changes depending on time according to the law of sine or cosine.
Let, for example, a material point with mass T suspended on a spring (Fig. 7.1, a). In this position, the elastic force F 1 balances the force of gravity mg. If you pull the spring a distance X(Fig. 7.1, b), then a large elastic force will act on the material point. The change in elastic force, according to Hooke's law, is proportional to the change in spring length or displacement X points:
F = -kh,(7.1)
Where To- spring stiffness; The minus sign shows that the force is always directed towards the equilibrium position: F< 0 at X> 0, F> 0 at X< 0.
Another example.
A mathematical pendulum is tilted from its equilibrium position by a small angle α (Fig. 7.2). Then the trajectory of the pendulum can be considered a straight line coinciding with the axis OH. In this case, the approximate equality
Where X- displacement of a material point relative to the equilibrium position; l- length of the pendulum thread.
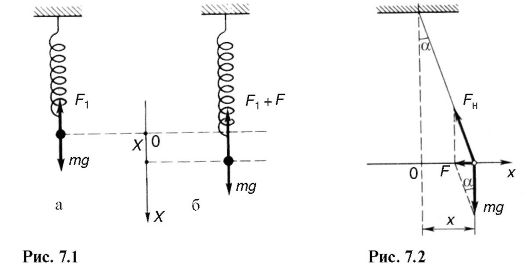
The material point (see Fig. 7.2) is acted upon by the tension force F H of the thread and the force of gravity mg. Their resultant is equal to:
Comparing (7.2) and (7.1), we see that in this example the resultant force is similar to elastic, since it is proportional to the displacement of the material point and is directed towards the equilibrium position. Such forces, inelastic in nature, but similar in properties to the forces that arise during minor deformations of elastic bodies, are called quasi-elastic.

Thus, a material point suspended on a spring (spring pendulum) or thread (mathematical pendulum) performs harmonic oscillations.


7.2. KINETIC AND POTENTIAL ENERGY OF VIBRATIONAL MOTION
The kinetic energy of an oscillating material point can be calculated by known formula, using expression (7.10):


7.3. ADDITION OF HARMONIC VIBRATIONS
A material point can simultaneously participate in several oscillations. In this case, in order to find the equation and trajectory of the resulting movement, one should add the oscillations. The easiest way to do this is to add harmonic vibrations.
Let's consider two such problems.
Addition of harmonic oscillations directed along one straight line.
Let a material point simultaneously participate in two oscillations occurring along one line. Analytically, such fluctuations are expressed by the following equations:


those. the amplitude of the resulting oscillation is equal to the sum of the amplitudes of the component oscillations if the difference in the initial phases is equal to an even number π (Fig. 7.8, a);
those. the amplitude of the resulting oscillation is equal to the difference in the amplitudes of the component oscillations if the difference in the initial phases is equal to an odd number π (Fig. 7.8, b). In particular, for A 1 = A 2 we have A = 0, i.e. there is no vibration (Fig. 7.8, c).
This is quite obvious: if a material point participates simultaneously in two oscillations that have the same amplitude and occur in antiphase, the point is motionless. If the frequencies of the added oscillations are not the same, then the complex oscillation will no longer be harmonic.
An interesting case is when the frequencies of the components of the oscillations differ little from each other: ω 01 and ω 02
The resulting oscillation is similar to a harmonic one, but with a slowly changing amplitude (amplitude modulation). Such oscillations are called beats(Fig. 7.9).
Addition of mutually perpendicular harmonic oscillations. Let a material point simultaneously participate in two oscillations: one is directed along the axis OH, the other - along the axis OY. The oscillations are given by the following equations:
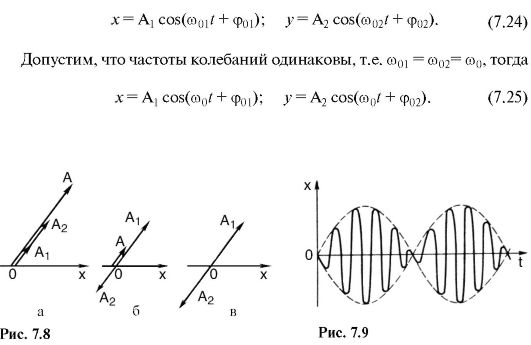
Equations (7.25) specify the trajectory of a material point in parametric form. If we substitute into these equations different meanings t, you can determine the coordinates X And y, and the set of coordinates is the trajectory.

Thus, with simultaneous participation in two mutually perpendicular harmonic oscillations of the same frequency, a material point moves along an elliptical path (Fig. 7.10).
Some special cases follow from expression (7.26):
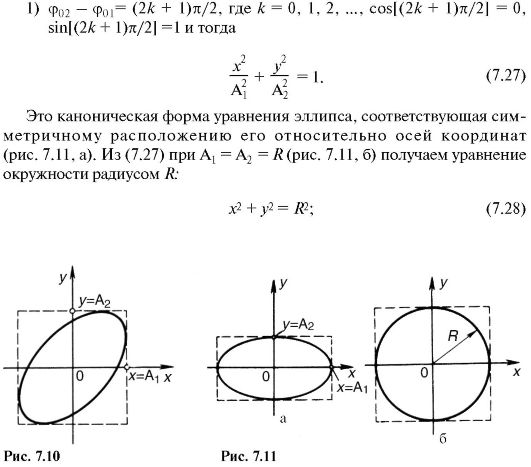

7.4. COMPLEX OSCILLATION. HARMONIC SPECTRUM OF COMPLEX VIBRATION
As can be seen from 7.3, the addition of vibrations leads to more complex modes of vibration. For practical purposes, the opposite operation is necessary: the decomposition of a complex vibration into simple, usually harmonic, vibrations.
Fourier showed that a periodic function of any complexity can be represented as a sum of harmonic functions, the frequencies of which are multiples of the frequency of the complex periodic function. This decomposition of a periodic function into harmonic ones and, consequently, the decomposition of various periodic processes (mechanical, electrical, etc.) into harmonic vibrations is called harmonic analysis. There are mathematical expressions that allow you to find the components of harmonic functions. Automatic harmonic analysis of vibrations, including for medical purposes, is carried out with special devices - analyzers.
The set of harmonic oscillations into which a complex oscillation is decomposed is called harmonic spectrum of a complex vibration.
It is convenient to imagine the harmonic spectrum as a set of frequencies (or circular frequencies) of individual harmonics together with their corresponding amplitudes. This representation is most clearly done graphically. As an example in Fig. 7.14, and the graphs of a complex oscillation are shown (curve 4) and its constituent harmonic vibrations (curves 1, 2 and 3); in Fig. Figure 7.14b shows the harmonic spectrum corresponding to this example.


Rice. 7.14, b
Harmonic analysis allows you to describe and analyze in sufficient detail any complex oscillatory process. It finds application in acoustics, radio engineering, electronics and other fields of science and technology.
7.5. DAMPED OSCILLATIONS
When studying harmonic vibrations, the forces of friction and resistance that exist in real systems were not taken into account. The action of these forces significantly changes the nature of the movement, the oscillation becomes fading.
If in the system, in addition to the quasi-elastic force, there are resistance forces of the medium (friction forces), then Newton’s second law can be written as follows:


The rate of decrease in the amplitude of oscillations is determined attenuation coefficient: the larger β, the stronger the inhibitory effect of the medium and the faster the amplitude decreases. In practice, however, the degree of attenuation is often characterized logarithmic attenuation decrement, meaning by this a value equal to natural logarithm the ratio of two successive oscillation amplitudes separated by a time interval equal to the oscillation period:

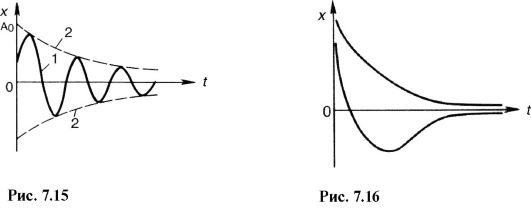
With strong damping (β 2 >>ω 2 0), formula (7.36) shows that the period of oscillation is an imaginary quantity. The movement in this case is already called aperiodic 1. Possible aperiodic movements are presented in the form of graphs in Fig. 7.16. This case, as applied to electrical phenomena, is discussed in more detail in Chap. 18.
Continuous (see 7.1) and damped oscillations called own or free They arise as a result of the initial displacement or initial velocity and occur in the absence of external influence due to the initially accumulated energy.
7.6. FORCED VIBRATIONS. RESONANCE
Forced vibrations are called oscillations that occur in a system with the participation of an external force that changes according to a periodic law.
Let us assume that the material point, in addition to the quasi-elastic force and the friction force, is acted upon by an external driving force:

1 Note that if some physical quantity takes on imaginary meanings, then this means some kind of unusualness, extraordinaryness of the corresponding phenomenon. In the example considered, the extraordinary thing is that the process ceases to be periodic.

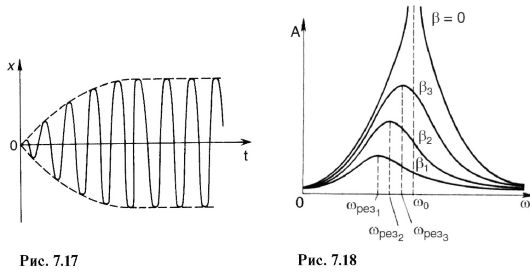
From (7.43) it is clear that in the absence of resistance (β=0) the amplitude of forced oscillations at resonance is infinitely large. Moreover, from (7.42) it follows that ω res = ω 0 - resonance in a system without damping occurs when the frequency of the driving force coincides with the frequency of natural oscillations. The graphical dependence of the amplitude of forced oscillations on the circular frequency of the driving force for different values of the damping coefficient is shown in Fig. 7.18.
Mechanical resonance can be both beneficial and harmful. The harmful effects of resonance are mainly due to the destruction it can cause. Thus, in technology, taking into account various vibrations, it is necessary to provide for the possible occurrence of resonant conditions, otherwise there may be destruction and disasters. Bodies usually have several natural vibration frequencies and, accordingly, several resonant frequencies.
If the attenuation coefficient of the internal organs of a person were small, then the resonance phenomena that arose in these organs under the influence of external vibrations or sound waves could lead to tragic consequences: rupture of organs, damage to ligaments, etc. However, such phenomena are practically not observed under moderate external influences, since the attenuation coefficient of biological systems is quite large. Nevertheless, resonance phenomena under the action of external mechanical vibrations occur in internal organs. This is apparently one of the reasons for the negative impact of infrasonic vibrations and vibrations on the human body (see 8.7 and 8.8).
7.7. SELF-OSCILLATIONS
As was shown in 7.6, oscillations can be maintained in a system even in the presence of resistance forces, if the system is periodically subjected to external influences (forced oscillations). This external influence does not depend on the oscillating system itself, while the amplitude and frequency of forced oscillations depend on this external influence.
However, there are also oscillatory systems that themselves regulate the periodic replenishment of wasted energy and therefore can oscillate for a long time.
Undamped oscillations that exist in any system in the absence of a variable external influence are called self-oscillations, and the systems themselves are called self-oscillatory.
The amplitude and frequency of self-oscillations depend on the properties of the self-oscillating system itself; unlike forced oscillations, they are not determined by external influences.
In many cases, self-oscillating systems can be represented by three main elements:
1) the oscillatory system itself;
2) source of energy;
3) regulator of energy supply to the oscillatory system itself.
Oscillatory system by channel feedback(Fig. 7.19) influences the regulator, informing the regulator about the state of this system.
A classic example of a mechanical self-oscillating system is a clock in which a pendulum or balance is an oscillatory system, a spring or a raised weight is a source of energy, and an anchor is a regulator of the flow of energy from the source into the oscillatory system.
Many biological systems (heart, lungs, etc.) are self-oscillating. A typical example of an electromagnetic self-oscillating system is generators of electromagnetic oscillations (see Chapter 23).

7.8. EQUATION OF MECHANICAL WAVES
A mechanical wave is a mechanical disturbance that propagates in space and carries energy.
There are two main types mechanical waves: elastic waves - propagation of elastic deformations - and waves on the surface of a liquid.
Elastic waves arise due to the connections that exist between particles of the medium: the movement of one particle from the equilibrium position leads to the movement of neighboring particles. This process propagates in space at a finite speed.
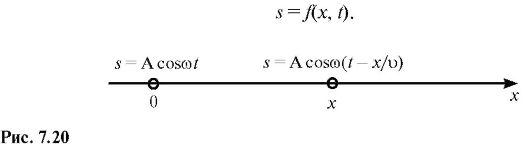
The wave equation expresses the displacement dependence s of an oscillating point participating in the wave process, from the coordinates of its equilibrium position and time.
For a wave propagating along a certain direction OX, this dependence is written in general form:
If s And X directed along one straight line, then the wave longitudinal, if they are mutually perpendicular, then the wave transverse
Let us derive the plane wave equation. Let the wave propagate along the axis X(Fig. 7.20) without damping so that the amplitudes of oscillations of all points are the same and equal to A. Let us set the oscillation of a point with the coordinate X= 0 (oscillation source) by the equation


Solving partial differential equations is beyond the scope of this course. One of the solutions (7.45) is known. However, it is important to note the following. If a change in any physical quantity: mechanical, thermal, electrical, magnetic, etc., corresponds to equation (7.49), then this means that the corresponding physical quantity propagates in the form of a wave with speed υ.
7.9. WAVE ENERGY FLOW. VECTOR UMOVA
The wave process is associated with energy transfer. A quantitative characteristic of transferred energy is energy flow.
The wave energy flux is equal to the ratio of the energy transferred by the waves through a certain surface to the time during which this energy is transferred:

The unit of wave energy flux is watt(W). Let us find the connection between the flow of wave energy and the energy of oscillating points and the speed of wave propagation.
Let us select the volume of the medium in which the wave propagates in the form of a rectangular parallelepiped (Fig. 7.21), the cross-sectional area of which is S, and the length of the edge is numerically equal to the speed v and coincides with the direction of propagation of the wave. In accordance with this, in 1 s through the platform S the energy possessed by the oscillating particles in the volume of the parallelepiped will pass through Sυ. This is the flow of wave energy:



7.10. SHOCK WAVES
One common example of a mechanical wave is sound wave(see Chapter 8). In this case, the maximum vibration speed of an individual air molecule is several centimeters per second, even for a sufficiently high intensity, i.e. it is significantly less than the speed of the wave (the speed of sound in air is about 300 m/s). This corresponds, as they say, to small disturbances of the environment.
However, with large disturbances (explosion, supersonic movement of bodies, powerful electric discharge, etc.), the speed of oscillating particles of the medium can already become comparable to the speed of sound, and a shock wave arises.
During an explosion, highly heated products with high density expand and compress layers of surrounding air. Over time, the volume of compressed air increases. The surface that separates compressed air from the unperturbed, in physics they call shock wave. The jump in gas density as a shock wave propagates through it is shown schematically in Fig. 7.22, a. For comparison, the same figure shows the change in the density of the medium during the passage of a sound wave (Fig. 7.22, b).
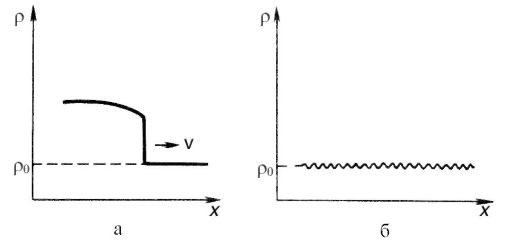
Rice. 7.22
The shock wave can have significant energy, so when nuclear explosion for the formation of a shock wave in environment about 50% of the explosion energy is consumed. Therefore, a shock wave, reaching biological and technical objects, can cause death, injury and destruction.
7.11. DOPPLER EFFECT
The Doppler effect is a change in the frequency of waves perceived by an observer (wave receiver) due to the relative movement of the wave source and the observer.



Mechanical vibrations propagating in an elastic medium (solid, liquid or gaseous) are called mechanical or elastic waves.
The process of propagation of vibrations in a continuous medium is called a wave process or wave. Particles of the medium in which the wave propagates are not drawn into translational motion by the wave. They only oscillate around their equilibrium positions. Together with the wave, only the state of oscillatory motion and its energy are transferred from particle to particle of the medium. That's why the main property of all waves, regardless of their nature, is the transfer of energy without transfer of matter.
Depending on the direction of particle vibrations relative to
to the direction in which the wave propagates, there are pro-
lobar And transverse waves.
Elastic wave called longitudinal, if the vibrations of the particles of the medium occur in the direction of wave propagation. Longitudinal waves are associated with volumetric tensile-compression deformation of the medium, therefore they can propagate both in solids and
in liquids and gaseous media.
x subject to shear deformation. Only solid bodies have this property.
λ In Fig. 6.1.1 presents the harmonic
dependence of the displacement of all particles of the medium on the distance to the source of oscillations at a given time. The distance between nearby particles vibrating in the same phase is called wavelength. The wavelength is also equal to the distance over which a certain phase of oscillation extends during the oscillation period
Not only particles located along the 0 axis oscillate X, but a collection of particles contained in a certain volume. The geometric location of the points to which the oscillations reach at the moment of time t, called wave front. The wave front is the surface that separates the part of space already involved in the wave process from the area in which oscillations have not yet arisen. The geometric location of points oscillating in the same phase is called wave surface. The wave surface can be drawn through any point in space covered by the wave process. Wave surfaces can be of any shape. In the simplest cases, they have the shape of a plane or sphere. Accordingly, the wave in these cases is called flat or spherical. In a plane wave, the wave surfaces are a set of planes parallel to each other, and in a spherical wave they are a set of concentric spheres.
Plane wave equation
The plane wave equation is an expression that gives the displacement of an oscillating particle as a function of its coordinates x, y, z and time t
| S=S(x,y,z,t). | (6.2.1) |
This function must be periodic both with respect to time t, and relative to the coordinates x, y, z. Periodicity in time follows from the fact that the displacement S describes the vibrations of a particle with coordinates x, y, z, and periodicity in coordinates follows from the fact that points spaced from each other at a distance equal to the wavelength vibrate in the same way.
Let us assume that the oscillations are harmonic in nature, and the axis 0 X coincides with the direction of wave propagation. Then the wave surfaces will be perpendicular to the 0 axis X and since everything
points of the wave surface oscillate equally, displacement S will depend only on the coordinate X and time t
Let us find the type of oscillation of points in the plane corresponding to an arbitrary value X. In order to travel the path from the plane X= 0 to plane X, the wave requires time τ = x/v. Consequently, vibrations of particles lying in the plane X, will lag in time by τ from particle oscillations in the plane X= 0 and described by the equation
| S(x;t)=A cosω( t− τ)+ϕ | = A cos | ω t − | x | +ϕ | . (6.2.4) | |||||
| υ |
Where A− wave amplitude; ϕ 0 – initial phase of the wave (determined by the choice of reference points X And t).
Let us fix some phase value ω( t − xυ) +ϕ 0 = const.
This expression defines the relationship between time t and that place X, in which the phase has a fixed value. Differentiating this expression, we get
Let us give the plane wave equation a symmetrical relative
strictly X And t view. To do this, we introduce the quantity k= 2 λ π, which is called
yes wave number, which can be represented in the form
We assumed that the amplitude of oscillations does not depend on X. For a plane wave, this is observed in the case when the wave energy is not absorbed by the medium. When propagating in an energy-absorbing medium, the intensity of the wave gradually decreases with distance from the source of oscillations, i.e., wave attenuation is observed. In a homogeneous medium, such attenuation occurs exponentially
law A = A 0 e −β x. Then the plane wave equation for the absorbing medium has the form
Where r r – radius vector, wave points; k = k ⋅n r − wave vector ; n r is the unit vector of the normal to the wave surface.
Wave vector− is a vector equal in magnitude to the wave number k and having the direction of the normal to the wave surface on-
| called. | |||
| Let's move from the radius vector of a point to its coordinates x, y, z | |||
| r | r | (6.3.2) | |
| k | ⋅r=k x x+k y y+k z z. | ||
| Then equation (6.3.1) will take the form | |||
| S(x,y,z;t)=A cos(ω t−k x x−k y y−k z z+ϕ 0). | (6.3.3) |
Let us establish the form of the wave equation. To do this, we find the second partial derivatives with respect to coordinates and time, expression (6.3.3)
| ∂ 2 S | r | r | |||||||||||||||||||||||||||||||||||
| ∂t | = −ω A cos | (ω t − k ⋅ r | +ϕ 0) = −ω S; | ||||||||||||||||||||||||||||||||||
| ∂ 2 S | r | r | |||||||||||||||||||||||||||||||||||
| ∂x | = − k x A cos(ω t − k | ⋅r | +ϕ 0) = − k x S | ||||||||||||||||||||||||||||||||||
| . | (6.3.4) | ||||||||||||||||||||||||||||||||||||
| ∂ 2 S | r | r | |||||||||||||||||||||||||||||||||||
| ∂y | = − k y A cos | (ω t − k ⋅ r | +ϕ 0) = − k y S; | ||||||||||||||||||||||||||||||||||
| ∂ 2 S | r | r | |||||||||||||||||||||||||||||||||||
| ∂z | = − k z A cos(ω t − k | ⋅r | +ϕ 0) = − k z S | ||||||||||||||||||||||||||||||||||
| Adding derivatives with respect to coordinates, and taking into account the derivative | |||||||||||||||||||||||||||||||||||||
| in time, we get | |||||||||||||||||||||||||||||||||||||
| ∂ | 2 | 2 | ∂ | 2 | ∂ | 2 | |||||||||||||||||||||||||||||||
| S 2 | + ∂ | S 2 | + | S 2 | = − (k x 2 + k y 2 + k z 2)S | = − k 2 S = | k | S 2 . | (6.3.5) | ||||||||||||||||||||||||||||
| ∂t | |||||||||||||||||||||||||||||||||||||
| ∂x | ∂y | ∂z | ω | ||||||||||||||||||||||||||||||||||
| 2 | |||||||||||||||||||||||||||||||||||||
| We will make a replacement | k | = | ω 2 | = | and we get the wave equation | ||||||||||||||||||||||||||||||||
| ω | υ | ω | υ | ||||||||||||||||||||||||||||||||||
| ∂ 2 S | + | ∂ 2 S | + | ∂ 2 S | = | 1 ∂ 2 S | or | S= | 1 ∂ 2 S | , | (6.3.6) | ||||||||||||||||||||||||||
| ∂x 2 | ∂y 2 | ∂z 2 | υ 2 ∂ t 2 | υ 2 ∂ t 2 | |||||||||||||||||||||||||||||||||
| where = | ∂ 2 | + | ∂ 2 | + | ∂ 2 | − Laplace operator. | |||||||||||||||||||||||||||||||
| ∂x 2 | ∂y 2 | ∂z 2 |




