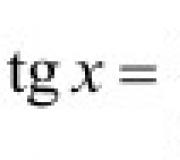Trigonometrija je jednostavna i jasna. Trigonometrija Objašnjene trigonometrijske funkcije

Kada izvodite trigonometrijske konverzije, slijedite ove savjete:

1. Nemojte odmah pokušavati smisliti shemu za rješavanje primjera od početka do kraja.
2. Ne pokušavajte odjednom pretvoriti cijeli primjer. Idite malim koracima naprijed.
3. Zapamtite da pored trigonometrijskih formula u trigonometriji, još uvijek možete koristiti sve poštene algebarske transformacije (zagrade, skraćivanje razlomaka, skraćene formule za množenje, itd.).
4. Vjerujte da će sve biti u redu.

Osnovne trigonometrijske formule

Većina formula u trigonometriji se često koristi i s desna na lijevo i s lijeva na desno, tako da morate naučiti ove formule tako dobro da možete lako primijeniti neku formulu u oba smjera. Zapišimo prvo definicije trigonometrijskih funkcija. Neka postoji pravougli trougao:

Zatim, definicija sinusa:

Definicija kosinusa:

Definicija tangente:

Definicija kotangensa:

Osnovni trigonometrijski identitet:

Najjednostavniji rezultati osnovnog trigonometrijskog identiteta:

Formule dvostrukog ugla. Sinus dvostrukog ugla:

Kosinus dvostrukog ugla:

Tangenta dvostrukog ugla:

Kotangens dvostrukog ugla:

Dodatne trigonometrijske formule

Trigonometrijske formule sabiranja. Sinus sume:

Sinus razlike:

Kosinus sume:

Kosinus razlike:

Tangent sume:

Tangenta razlike:

Kotangens iznosa:

Kotangens razlike:

Trigonometrijske formule za pretvaranje sume u proizvod. Zbir sinusa:

Sinusna razlika:

Zbir kosinusa:

Razlika kosinusa:

Zbir tangenti:

Tangentna razlika:

Zbir kotangensa:

Kotangens razlika:

Trigonometrijske formule za pretvaranje proizvoda u zbir. Proizvod sinusa:

Umnožak sinusa i kosinusa:

Umnožak kosinusa:

Formule za smanjenje stepena.

Formule poluugla.

Formule trigonometrijske redukcije

Poziva se kosinusna funkcija kofunkcija sinusne funkcije i obrnuto. Slično, tangentne i kotangensne funkcije su kofunkcije. Formule redukcije mogu se formulirati prema sljedećem pravilu:

• Ako se u formuli redukcije ugao oduzme (doda) od 90 stepeni ili 270 stepeni, onda se redukovana funkcija menja u kofunkciju;
• Ako se u formuli redukcije ugao oduzme (doda) od 180 stepeni ili 360 stepeni, tada se zadržava naziv redukovane funkcije;
• U ovom slučaju, znak koji redukovana (tj. originalna) funkcija ima u odgovarajućem kvadrantu stavlja se ispred redukovane funkcije, ako smatramo da je oduzeti (dodati) ugao oštar.

Formule redukcije date su u obliku tabele:

By trigonometrijski krug lako odrediti tabelarne vrijednosti trigonometrijskih funkcija:

Trigonometrijske jednadžbe

Da bi se riješila određena trigonometrijska jednačina, ona se mora svesti na jednu od najjednostavnijih trigonometrijskih jednadžbi, o kojoj će biti riječi u nastavku. Za ovo:

• Možete koristiti trigonometrijske formule date gore. U isto vrijeme, ne morate pokušavati transformirati cijeli primjer odjednom, već morate ići naprijed malim koracima.
• Ne smijemo zaboraviti na mogućnost transformacije nekog izraza algebarskim metodama, tj. na primjer, izvadite nešto iz zagrada ili, obrnuto, otvorite zagrade, smanjite razlomak, primijenite skraćenu formulu množenja, dovedite razlomke u zajednički nazivnik itd.
• Prilikom rješavanja trigonometrijskih jednadžbi možete koristiti metod grupisanja. Treba imati na umu da da bi proizvod nekoliko faktora bio jednak nuli, dovoljno je da bilo koji od njih bude jednak nuli, i ostalo je postojalo.
• Primjena varijabilna metoda zamjene, kao i obično, jednadžba nakon uvođenja zamjene treba da postane jednostavnija i da ne sadrži originalnu varijablu. Također morate zapamtiti da izvršite obrnutu zamjenu.
• Zapamtite da se homogene jednadžbe često pojavljuju u trigonometriji.
• Kada otvarate module ili rješavate iracionalne jednadžbe s trigonometrijskim funkcijama, morate zapamtiti i uzeti u obzir sve suptilnosti rješavanja odgovarajućih jednadžbi s običnim funkcijama.
• Zapamtite ODZ (u trigonometrijskim jednadžbama ograničenja na ODZ uglavnom se svode na to da ne možete dijeliti sa nulom, ali ne zaboravite na druga ograničenja, posebno na pozitivnost izraza u racionalnim potencijama i pod korijenima parnih potencija). Također zapamtite da vrijednosti sinusa i kosinusa mogu biti samo u rasponu od minus jedan do plus jedan, uključujući.

Glavna stvar je, ako ne znate što da radite, učinite barem nešto, a glavna stvar je da pravilno koristite trigonometrijske formule. Ako ono što dobijete postaje sve bolje i bolje, onda nastavite s rješenjem, a ako se pogorša, vratite se na početak i pokušajte primijeniti druge formule, činite to dok ne naiđete na ispravno rješenje.

Formule za rješenja najjednostavnijih trigonometrijskih jednadžbi. Za sinus postoje dva ekvivalentna oblika pisanja rješenja:

Za ostale trigonometrijske funkcije, notacija je nedvosmislena. za kosinus:

za tangentu:

za kotangens:

Rješavanje trigonometrijskih jednadžbi u nekim posebnim slučajevima:

Uspješna, marljiva i odgovorna implementacija ove tri tačke omogućit će vam da na CT-u pokažete odličan rezultat, maksimum onoga za što ste sposobni.

Našli ste grešku?

Ako mislite da ste pronašli grešku u materijalima za obuku, napišite o tome putem e-pošte. Također možete prijaviti grešku na društvenoj mreži (). U pismu naznačite predmet (fizika ili matematika), naziv ili broj teme ili testa, broj zadatka ili mjesto u tekstu (stranici) na kojem, po vašem mišljenju, postoji greška. Također opišite o čemu se sumnja na grešku. Vaše pismo neće proći nezapaženo, greška će biti ili ispravljena, ili će Vam biti objašnjeno zašto nije greška.

Očuvanje vaše privatnosti nam je važno. Iz tog razloga smo razvili Politiku privatnosti koja opisuje kako koristimo i pohranjujemo vaše podatke. Pregledajte našu praksu privatnosti i javite nam ako imate pitanja.

Prikupljanje i korištenje ličnih podataka

Lični podaci odnose se na podatke koji se mogu koristiti za identifikaciju ili kontaktiranje određene osobe.

Od vas se može tražiti da unesete svoje lične podatke u bilo koje vrijeme kada nas kontaktirate.

U nastavku su navedeni neki primjeri vrsta ličnih podataka koje možemo prikupljati i kako ih možemo koristiti.

Koje lične podatke prikupljamo:

• Kada podnesete prijavu na stranici, možemo prikupljati različite informacije, uključujući vaše ime, broj telefona, adresu e-pošte itd.

Kako koristimo vaše lične podatke:

• Lični podaci koje prikupljamo omogućavaju nam da vas kontaktiramo s jedinstvenim ponudama, promocijama i drugim događajima i nadolazećim događajima.
• S vremena na vrijeme možemo koristiti vaše lične podatke za slanje važnih obavijesti i komunikacija.
• Lične podatke možemo koristiti i za interne svrhe, kao što su provođenje revizija, analiza podataka i različita istraživanja kako bismo poboljšali usluge koje pružamo i dali vam preporuke u vezi s našim uslugama.
• Ako učestvujete u nagradnoj igri, natjecanju ili sličnoj promociji, možemo koristiti informacije koje nam date za upravljanje takvim programima.

Otkrivanje informacija trećim licima

Podatke koje dobijemo od vas ne otkrivamo trećim licima.

Izuzeci:

• Ako je potrebno - u skladu sa zakonom, sudskim postupkom, u sudskom postupku, i/ili na osnovu javnih zahtjeva ili zahtjeva državnih organa na teritoriji Ruske Federacije - otkriti vaše lične podatke. Takođe možemo otkriti informacije o vama ako utvrdimo da je takvo otkrivanje neophodno ili prikladno za sigurnosne, provođenje zakona ili druge svrhe od javnog značaja.
• U slučaju reorganizacije, spajanja ili prodaje, možemo prenijeti lične podatke koje prikupimo na odgovarajuću treću stranu.

Zaštita ličnih podataka

Poduzimamo mjere opreza - uključujući administrativne, tehničke i fizičke - da zaštitimo vaše osobne podatke od gubitka, krađe i zloupotrebe, kao i neovlaštenog pristupa, otkrivanja, izmjene i uništenja.

Poštivanje vaše privatnosti na nivou kompanije

Kako bismo osigurali da su vaši lični podaci sigurni, našim zaposlenima prenosimo standarde privatnosti i sigurnosti i striktno provodimo praksu privatnosti.

U ovoj lekciji ćemo naučiti definicije trigonometrijske funkcije i njihova osnovna svojstva, naučite kako raditi sa trigonometrijski krug, hajde da saznamo šta je to period funkcije i zapamtite razne načini mjerenja uglova. Osim toga, razumjet ćemo upotrebu formule redukcije.

Ova lekcija će vam pomoći da se pripremite za jednu od vrsta zadataka U 7.

Priprema za Jedinstveni državni ispit iz matematike

Eksperimentiraj

Lekcija 7.Uvod u trigonometriju.

Teorija

Sažetak lekcije

Danas započinjemo rubriku koja za mnoge nosi zastrašujući naziv „Trigonometrija“. Odmah da razjasnimo da ovo nije zaseban predmet po imenu sličan geometriji, kako neki misle. Iako prevedena s grčkog, riječ "trigonometrija" znači "mjera trouglova" i direktno je povezana sa geometrijom. Osim toga, trigonometrijski proračuni se široko koriste u fizici i tehnologiji. Ali počet ćemo s razmatranjem kako se osnovne trigonometrijske funkcije uvode u geometriju koristeći pravokutni trokut.

Upravo smo upotrijebili izraz “trigonometrijska funkcija” - to znači da ćemo uvesti čitavu klasu određenih zakona korespondencije između jedne i druge varijable.

Da biste to učinili, uzmite u obzir pravokutni trokut, u kojem se, radi praktičnosti, koriste standardne oznake za stranice i kutove, što možete vidjeti na slici:

Razmotrite, na primjer, ugaoi za to unesite sljedeće radnje:

Nazovimo odnos suprotne strane prema sinusu hipotenuze, tj.

Nazovimo omjer susjednog kraka i kosinusa hipotenuze, tj. ;

Omjer suprotne i susjedne strane nazivat ćemo tangentom, tj. ;

Odnos susedne i suprotne strane nazivaćemo kotangensom, tj. .

Sve ove radnje sa uglom se nazivaju trigonometrijske funkcije. Sam ugao se obično naziva argument trigonometrijske funkcije i može se označiti, na primjer, sa X, kao što je uobičajeno u algebri.

Važno je odmah shvatiti da trigonometrijske funkcije ovise posebno o kutu u pravokutnom trokutu, a ne o njegovim stranicama. To je lako dokazati ako uzmemo u obzir trokut sličan ovome, u kojem će dužine stranica biti različite, ali se svi uglovi i omjeri stranica neće mijenjati, tj. Trigonometrijske funkcije uglova će također ostati nepromijenjene.

Nakon ove definicije trigonometrijskih funkcija, može se postaviti pitanje: “Da li postoji npr.? Uostalom, ugaone može biti u pravouglom trouglu» . Čudno je da je odgovor na ovo pitanje potvrdan, a vrijednost ovog izraza je jednaka , a to je još više iznenađujuće, jer su sve trigonometrijske funkcije omjer stranica pravokutnog trokuta, a dužine stranica su pozitivni brojevi.

Ali u tome nema paradoksa. Činjenica je da je, na primjer, u fizici, pri opisivanju nekih procesa, potrebno koristiti trigonometrijske funkcije uglova ne samo velikih, već i velikih i ravnomjernih. Za to je potrebno uvesti općenitije pravilo za izračunavanje trigonometrijskih funkcija pomoću tzv. "jedinični trigonometrijski krug".

To je kružnica jediničnog polumjera, nacrtana tako da mu je centar u početku kartezijanske ravni.

Da biste prikazali uglove u ovom krugu, morate se dogovoriti odakle ih postaviti. Prihvaćeno je uzeti pozitivan smjer ose apscise kao referentnu zraku kuta, tj. x-osa. Smatra se da je smjer taloženja uglova u smjeru suprotnom od kazaljke na satu. Na osnovu ovih sporazuma, prvo ostavimo po strani oštar ugao. Za takve oštre kutove već znamo kako izračunati vrijednosti trigonometrijskih funkcija u pravokutnom trokutu. Ispostavilo se da pomoću prikazanog kruga možete izračunati i trigonometrijske funkcije, samo što je pogodnije.

Vrijednosti sinusa i kosinusa oštrog ugla su koordinate točke presjeka stranice ovog kuta s jediničnim krugom:

Ovo se može napisati ovako:

:

Na osnovu činjenice da koordinate duž x-ose pokazuju vrijednost kosinusa, a koordinate duž y-ose pokazuju vrijednost sinusa ugla, zgodno je preimenovati nazive osi u koordinatnom sistemu sa jediničnim krugom kao što vidite na slici:

Os apscisa je preimenovana u os kosinusa, a osa ordinata u os sinusa.

Specificirano pravilo za određivanje sinusa i kosinusa generalizirano je i na tupe uglove i na uglove koji se nalaze u rasponu od do. U ovom slučaju, sinusi i kosinusi mogu poprimiti i pozitivne i negativne vrijednosti. Razno znakove vrijednosti ovih trigonometrijskih funkcija u zavisnosti od toga u koju četvrtinu pada dotični ugao, uobičajeno je da se prikaže na sledeći način:

Kao što možete vidjeti, predznaci trigonometrijskih funkcija određeni su pozitivnim i negativnim smjerovima njihovih odgovarajućih osa.

Osim toga, vrijedi obratiti pažnju na činjenicu da budući da je najveća koordinata točke na jediničnom krugu i duž apscise i ordinatne ose jednaka jedan, a najmanja je minus jedan, tada vrijednosti sinusa i kosinusa ograničeno na ove brojeve:

Ovi zapisi se takođe obično pišu u ovom obliku:

Da bi se uvele funkcije tangente i kotangensa na trigonometrijsku kružnicu, potrebno je nacrtati dodatne elemente: tangentu na kružnicu u tački A - iz nje se određuje vrijednost tangente kuta, a tangentu na u tačka B - iz nje se određuje vrijednost kotangensa ugla.

Međutim, nećemo se upuštati u definiciju tangenta i kotangensa na trigonometrijskom krugu, jer lako se mogu izračunati poznavanjem vrijednosti sinusa i kosinusa datog ugla, što već znamo kako da radimo. Ako ste zainteresovani da naučite kako da izračunate tangentu i kotangens na trigonometrijskom krugu, pregledajte nastavni plan i program predmeta algebra za 10. razred.

Označavamo samo sliku na krugu znaci tangenti i kotangensi zavisno od ugla:

Imajte na umu da, slično rasponima vrijednosti sinusa i kosinusa, možete specificirati raspon vrijednosti tangenta i kotangensa. Na osnovu njihove definicije o trigonometrijskom krugu, značenja ovih funkcija nisu ograničena:

Šta se još može ovako napisati:

Pored uglova u rasponu od do, trigonometrijski krug vam omogućava da radite sa uglovima koji su veći, pa čak i sa negativnim uglovima. Takve vrijednosti uglova, iako se čine besmislenim za geometriju, koriste se za opisivanje nekih fizičkih procesa. Na primjer, kako odgovarate na pitanje: "Za koji će se ugao kazaljka na satu okrenuti za jedan dan?" Za to vrijeme obaviće dva puna obrtaja, a u jednoj revoluciji će proći, tj. u roku od jednog dana će se pretvoriti u . Kao što vidite, takve vrijednosti imaju vrlo praktično značenje. Znakovi uglova se koriste za označavanje smjera rotacije - jedan od smjerova je dogovoreno da se mjeri pozitivnim uglovima, a drugi negativnim. Kako se to može uzeti u obzir u trigonometrijskom krugu?

Na krugu s takvim uglovima rade na sljedeći način:

1) Uglovi koji su veći od , iscrtani su u smjeru suprotnom od kazaljke na satu, prolazeći kroz ishodište onoliko puta koliko je potrebno. Na primjer, da biste konstruirali ugao, morate proći kroz dva puna okretaja i još jedan. Sve trigonometrijske funkcije se izračunavaju za konačnu poziciju. Lako je vidjeti da će vrijednosti svih trigonometrijskih funkcija za i za biti iste.

2) Negativni uglovi su postavljeni potpuno po istom principu kao i pozitivni, samo u smeru kazaljke na satu.

Samo metodom konstruisanja velikih uglova možemo zaključiti da su vrednosti sinusa i kosinusa uglova koji se razlikuju po iste. Ako analiziramo vrijednosti tangenta i kotangensa, one će biti iste za uglove koji se razlikuju za .

Takvi minimalni brojevi različiti od nule, kada se dodaju argumentu, ne mijenjaju vrijednost funkcije, se pozivaju period ovu funkciju.

dakle, periodsinus i kosinus su jednaki, te tangenta i kotangensa. To znači da bez obzira koliko dodajete ili oduzimate ove periode od uglova koji se razmatraju, vrijednosti trigonometrijskih funkcija se neće promijeniti.

Na primjer, , i sl.

Kasnije ćemo se vratiti na detaljnije objašnjenje i primjenu ovog svojstva trigonometrijskih funkcija.

Postoje određene veze između trigonometrijskih funkcija istog argumenta koje se vrlo često koriste i nazivaju osnovni trigonometrijski identiteti.

izgledaju ovako:

1) , takozvana "trigonometrijska jedinica"

3)

4)

5)

Imajte na umu da, na primjer, notacija znači da je cijela trigonometrijska funkcija na kvadratu. One. može se predstaviti u ovom obliku: . Važno je shvatiti da to nije jednako notaciji kao što je , u ovom slučaju je samo argument na kvadrat, a ne cijela funkcija, a osim toga, izrazi ovog tipa su izuzetno rijetki.

Postoje dvije vrlo korisne posljedice iz prvog identiteta koje mogu biti korisne u rješavanju mnogih vrsta problema. Nakon jednostavnih transformacija, možete izraziti sinus kroz kosinus istog ugla i obrnuto:

Pojavljuju se dva moguća znaka izraza jer uzimanje aritmetičkog kvadratnog korijena daje samo nenegativne vrijednosti, a sinus i kosinus, kao što smo već vidjeli, mogu imati negativne vrijednosti. Štoviše, najprikladnije je odrediti znakove ovih funkcija pomoću trigonometrijskog kruga, ovisno o tome koji kutovi su prisutni u njima.

Sada se prisjetimo da se uglovi mogu mjeriti na dva načina: u stepenima i u radijanima. Hajde da navedemo definicije jednog stepena i jednog radijana.

Jedan stepen- ovo je ugao formiran od dva poluprečnika koji savijaju luk jednak krugu.

Jedan radijan- ovo je ugao koji čine dva poluprečnika savijena lukom jednakim po dužini poluprečniku.

One. oni su jednostavno dva različita načina mjerenja uglova koji su apsolutno jednaki. U opisivanju fizičkih procesa koje karakteriziraju trigonometrijske funkcije, uobičajeno je koristiti radijansku mjeru uglova, pa ćemo se i na nju morati naviknuti.

Uobičajeno je mjeriti uglove u radijanima u ulomcima pi, na primjer, ili. U ovom slučaju, vrijednost broja "pi", koji je jednak 3,14, može se zamijeniti, ali se to rijetko radi.

Za pretvaranje stepena mjere uglova u radijane iskoristiti činjenicu da je kut , iz kojeg je lako dobiti opću formulu za prevođenje:

Na primjer, pretvorimo u radijane: .

Postoji i suprotno formulakonverzija iz radijana u stepene:

Na primjer, pretvorimo u stupnjeve: .

U ovoj temi ćemo često koristiti radijansku mjeru ugla.

Sada je vrijeme da se prisjetimo koje specifične vrijednosti mogu dati trigonometrijske funkcije različitih uglova. Za neke uglove koji su višestruki od , postoji tablica vrijednosti trigonometrijskih funkcija. Radi praktičnosti, uglovi su dati u stepenu i radijanskim mjerama.

Ovi uglovi se često susreću u mnogim problemima i preporučljivo je da se možete pouzdano kretati u ovoj tabeli. Vrijednosti tangenta i kotangensa nekih uglova nemaju smisla, što je u tabeli označeno crticama. Razmislite sami zašto je to tako ili pročitajte o tome detaljnije u prilogu za lekciju.

Posljednja stvar s kojom se trebamo upoznati na našoj prvoj lekciji trigonometrije je transformacija trigonometrijskih funkcija korištenjem tzv. redukcijskih formula.

Ispostavilo se da postoji određena vrsta izraza za trigonometrijske funkcije koja je prilično uobičajena i zgodno pojednostavljena. Na primjer, ovo su izrazi: itd.

One. Govorit ćemo o funkcijama koje kao argument uzimaju proizvoljan ugao, promijenjen na cijeli ili polovični dio. Takve funkcije su pojednostavljene na argument koji je jednak proizvoljnom kutu sabiranja ili oduzimanja dijelova. Na primjer, , A . Kao što vidite, rezultat može biti suprotna funkcija, a funkcija može promijeniti predznak.

Stoga se pravila za transformaciju takvih funkcija mogu podijeliti u dvije faze. Prvo morate odrediti koju funkciju ćete dobiti nakon transformacije:

1) Ako se proizvoljni argument promijeni u cijeli broj, tada se funkcija ne mijenja. Ovo vrijedi za funkcije tipa , gdje je bilo koji cijeli broj;

Nekada je u školi postojao poseban kurs za izučavanje trigonometrije. Certifikat je sadržavao ocjene iz tri matematičke discipline: algebra, geometrija i trigonometrija.

Zatim, kao dio reforme školskog obrazovanja, trigonometrija je prestala postojati kao poseban predmet. U modernoj školi, prvo upoznavanje sa trigonometrijom dešava se u predmetu geometrije 8. razreda. Detaljnije proučavanje ovog predmeta nastavlja se u kursu algebre 10. razreda.

Definicije sinusa, kosinusa, tangente i kotangensa prvo su date u geometriji kroz odnos stranica pravokutnog trokuta.

Oštar ugao u pravokutnom trokutu je omjer suprotne strane i hipotenuze.

Kosinus Oštar ugao u pravokutnom trokutu je omjer susjednog kraka i hipotenuze.

Tangenta Oštar ugao u pravokutnom trokutu je omjer suprotne i susjedne strane.

Kotangens Oštar ugao u pravokutnom trokutu je omjer susjedne i suprotne strane.

Ove definicije važe samo za oštre uglove (0º do 90°).

Na primjer,

u trouglu ABC, gde je ∠C=90°, BC je krak suprotan uglu A, AC je krak susedan uglu A, AB je hipotenuza.

Predmet algebre 10. razreda uvodi definicije sinusa, kosinusa, tangenta i kotangensa za bilo koji ugao (uključujući negativan).

Posmatrajmo kružnicu poluprečnika R sa centrom u početku - tačkom O(0;0). Označimo točku presjeka kružnice sa pozitivnim smjerom ose apscise kao P 0 .

U geometriji se ugao smatra dijelom ravnine ograničene s dvije zrake. Sa ovom definicijom, ugao varira od 0° do 180°.

U trigonometriji se ugao smatra rezultatom rotacije zraka OP 0 oko početne tačke O.

Istovremeno, složili su se da smatraju okretanje snopa suprotno od kazaljke na satu kao pozitivan smjer kretanja, a u smjeru kazaljke na satu kao negativan (ovaj dogovor je povezan sa pravim kretanjem Sunca oko Zemlje).

Na primjer, kada je zraka OP 0 rotirana oko tačke O za ugao α suprotno od kazaljke na satu, tačka P 0 će ići u tačku P α,

pri skretanju za ugao α u smjeru kazaljke na satu - do tačke F.

Sa ovom definicijom, ugao može poprimiti bilo koju vrijednost.

Ako nastavimo rotirati snop OP 0 u smjeru suprotnom od kazaljke na satu, pri okretanju kroz ugao α°+360°, α°+360°·2,...,α°+360°·n, gdje je n cijeli broj (n∈ Ζ), opet idemo do tačke P α:

Uglovi se mjere u stepenima i radijanima.

1° je ugao jednak 1/180 stepena mere razvijenog ugla.

1 radijan je centralni ugao čija je dužina luka jednaka poluprečniku kružnice:

∠AOB=1 rad.

Radijanski simboli se obično ne pišu. Oznaka stepena se ne može izostaviti iz evidencije.

Na primjer,

Tačka P α , dobijena iz tačke P 0 rotacijom zraka OP 0 oko tačke O za ugao α suprotno od kazaljke na satu, ima koordinate P α (x;y).

Ispustimo okomitu P α A iz tačke P α na osu apscise.

U pravokutnom trokutu OP α A:

P α A - noga suprotna od ugla α,

OA - krak uz ugao α,

OP α je hipotenuza.

P α A=y, OA=x, OP α =R.

Po definiciji sinusa, kosinusa, tangente i kotangensa u pravokutnom trokutu imamo:

Dakle, u slučaju kružnice sa centrom u početku proizvoljnog radijusa sine ugao α je odnos ordinate tačke P α i dužine poluprečnika.

Kosinus ugao α je odnos apscise tačke P α i dužine poluprečnika.

Tangenta ugao α je omjer ordinate tačke P α prema njenoj apscisi.

Kotangens ugao α je odnos apscise tačke P α i njene ordinate.

Vrijednosti sinusa, kosinusa, tangenta i kotangensa ovise samo o vrijednosti α i ne ovise o dužini polumjera R (ovo slijedi iz sličnosti krugova).

Stoga je pogodno odabrati R=1.

Krug sa centrom u početku i poluprečnikom R=1 naziva se jedinični krug.

Definicije

1) Sinus ugao α naziva se ordinata tačke P α (x;y) jedinične kružnice:

2) Kosinus ugao α naziva se apscisa tačke P α (x;y) jedinične kružnice:

3) Tangenta ugao α je omjer ordinate tačke P α (x;y) i njene apscise, odnosno omjer sinα prema cosα (gdje je cosα≠0):

4) Kotangens ugao α je odnos apscise tačke P α (x;y) i njene ordinate, odnosno odnos cosα i sinα (gde je sinα≠0):

Ovako uvedene definicije nam omogućavaju da razmotrimo ne samo trigonometrijske funkcije uglova, već i trigonometrijske funkcije numeričkih argumenata (ako smatramo sinα, cosα, tanα i ctgα kao odgovarajuće trigonometrijske funkcije ugla u α radijanima, tj. sinus broja α je sinus ugla u α radijanima, kosinus broja α je kosinus ugla u α radijanima, itd.).

Svojstva trigonometrijskih funkcija izučavaju se kao posebna tema u predmetu algebra u 10. ili 11. razredu. Trigonometrijske funkcije se široko koriste u fizici.

Sinus, kosinus, tangenta - kada izgovarate ove riječi u prisustvu srednjoškolaca, možete biti sigurni da će dvije trećine njih izgubiti interes za dalji razgovor. Razlog leži u činjenici da se osnove trigonometrije u školi uče u potpunoj izolaciji od stvarnosti, te stoga učenici ne vide smisao u proučavanju formula i teorema.

Zapravo, pomnijim ispitivanjem, ova oblast znanja pokazuje se vrlo zanimljivom, ali i primijenjenom - trigonometrija se koristi u astronomiji, građevinarstvu, fizici, muzici i mnogim drugim oblastima.

Hajde da se upoznamo sa osnovnim pojmovima i navedemo nekoliko razloga za proučavanje ove grane matematičke nauke.

Priča

Nepoznato je u kom trenutku je čovečanstvo počelo da stvara buduću trigonometriju od nule. Međutim, dokumentirano je da su Egipćani već u drugom mileniju prije Krista bili upoznati s osnovama ove nauke: arheolozi su pronašli papirus sa zadatkom u kojem je bilo potrebno pronaći ugao nagiba piramide na dvije poznate strane.

Naučnici Drevnog Babilona postigli su ozbiljnije uspjehe. Tokom vekova, proučavajući astronomiju, savladali su niz teorema, uveli posebne metode za merenje uglova, koje, inače, koristimo i danas: stepene, minute i sekunde posudila je evropska nauka u grčko-rimskoj kulturi, u koju ove jedinice potiču od Babilonaca.

Pretpostavlja se da je poznata Pitagorina teorema, koja se odnosi na osnove trigonometrije, bila poznata Vaviloncima prije skoro četiri hiljade godina.

Ime

Doslovno, pojam "trigonometrija" može se prevesti kao "mjerenje trouglova". Glavni predmet proučavanja u ovom dijelu nauke dugi niz stoljeća bio je pravokutni trokut, tačnije, odnos između veličina uglova i dužina njegovih stranica (danas proučavanje trigonometrije od nule počinje ovim dijelom) . U životu se često dešavaju situacije kada je praktički nemoguće izmjeriti sve potrebne parametre nekog objekta (ili udaljenost do objekta), a tada je potrebno proračunima dobiti podatke koji nedostaju.

Na primjer, u prošlosti ljudi nisu mogli mjeriti udaljenost do svemirskih objekata, ali pokušaji izračunavanja ovih udaljenosti dogodili su se mnogo prije dolaska naše ere. Trigonometrija je također igrala ključnu ulogu u navigaciji: uz određeno znanje, kapetan je uvijek mogao noću navigirati po zvijezdama i prilagoditi kurs.

Osnovni koncepti

Savladavanje trigonometrije od nule zahtijeva razumijevanje i pamćenje nekoliko osnovnih pojmova.

Sinus određenog ugla je omjer suprotne strane prema hipotenuzi. Pojasnimo da je suprotna noga strana koja leži nasuprot ugla koji razmatramo. Dakle, ako je ugao 30 stepeni, sinus ovog ugla će uvek, za bilo koju veličinu trougla, biti jednak ½. Kosinus ugla je omjer susjednog kraka i hipotenuze.

Tangenta je omjer suprotne i susjedne strane (ili, što je isto, omjer sinusa i kosinusa). Kotangens je jedinica podijeljena tangentom.

Vrijedi spomenuti poznati broj Pi (3,14...), koji je polovina dužine kruga poluprečnika jedne jedinice.

Popularne greške

Ljudi koji uče trigonometriju od nule prave brojne greške – uglavnom zbog nepažnje.

Prvo, kada rješavate probleme geometrije, morate zapamtiti da je upotreba sinusa i kosinusa moguća samo u pravokutnom trokutu. Dešava se da učenik „automatski“ uzme najdužu stranu trougla kao hipotenuzu i dobije netačne rezultate proračuna.

Drugo, u početku je lako pobrkati vrijednosti sinusa i kosinusa za odabrani kut: podsjetite da je sinus od 30 stupnjeva numerički jednak kosinusu od 60, i obrnuto. Ako zamenite netačan broj, svi dalji proračuni će biti netačni.

Treće, dok se problem u potpunosti ne riješi, ne biste trebali zaokružiti nijednu vrijednost, izdvojiti korijene ili pisati običan razlomak kao decimalu. Često učenici nastoje da dobiju "lijep" broj u trigonometrijskom zadatku i odmah izvuku korijen od tri, iako se nakon tačno jedne radnje ovaj korijen može smanjiti.

Etimologija riječi "sinus"

Istorija riječi "sinus" je zaista neobična. Činjenica je da bukvalni prijevod ove riječi sa latinskog znači "šuplji". To je zato što se pravilno razumijevanje riječi izgubilo tokom prijevoda s jednog jezika na drugi.

Nazivi osnovnih trigonometrijskih funkcija potječu iz Indije, gdje je pojam sinusa na sanskrtu označavan riječju "žica" - činjenica je da je segment, zajedno sa lukom kruga na kojem je počivao, izgledao kao luk . Za vrijeme procvata arapske civilizacije posuđena su indijska dostignuća u oblasti trigonometrije, a termin je prešao u arapski kao transkripcija. Dogodilo se da je ovaj jezik već imao sličnu riječ koja označava depresiju, a ako su Arapi razumjeli fonetsku razliku između domaće i posuđene riječi, onda su Evropljani, prevodeći naučne rasprave na latinski, greškom doslovno preveli arapsku riječ, koja nije imala ništa. u vezi sa konceptom sinusa. I danas ga koristimo.

Tabele vrijednosti

Postoje tablice koje sadrže numeričke vrijednosti za sinuse, kosinuse i tangente svih mogućih uglova. U nastavku predstavljamo podatke za uglove od 0, 30, 45, 60 i 90 stepeni, koji se moraju naučiti kao obavezni dio trigonometrije za "lutke", na sreću, prilično ih je lako zapamtiti.

Ako vam se desi da vam brojčana vrijednost sinusa ili kosinusa nekog ugla "izleti iz glave", postoji način da to sami izvedete.

Geometrijski prikaz

Nacrtajmo kružnicu i povučemo apscisu i ordinatnu os kroz njegovo središte. Os apscisa je horizontalna, a osa ordinata okomita. Obično se potpisuju kao "X" i "Y" respektivno. Sada ćemo povući ravnu liniju iz središta kruga tako da se dobije ugao koji nam je potreban između nje i X ose. Konačno, iz tačke u kojoj prava linija seče kružnicu, ispuštamo okomitu na osu X, dužina rezultujućeg segmenta će biti jednaka brojčanoj vrednosti sinusa našeg ugla.

Ova metoda je vrlo relevantna ako ste zaboravili traženu vrijednost, na primjer, tokom ispita, a nemate udžbenik trigonometrije pri ruci. Na ovaj način nećete dobiti tačan broj, ali ćete sigurno vidjeti razliku između ½ i 1,73/2 (sinus i kosinus ugla od 30 stepeni).

Aplikacija

Neki od prvih stručnjaka koji su koristili trigonometriju bili su mornari koji nisu imali drugu referentnu tačku na otvorenom moru osim neba iznad svojih glava. Danas, kapetani brodova (aviona i drugih vidova transporta) ne traže najkraći put koristeći zvijezde, već aktivno pribjegavaju GPS navigaciji, što bi bilo nemoguće bez upotrebe trigonometrije.

U gotovo svakom dijelu fizike naći ćete proračune pomoću sinusa i kosinusa: bilo da se radi o primjeni sile u mehanici, proračunima putanje objekata u kinematici, vibracijama, širenju valova, prelamanju svjetlosti - jednostavno ne možete bez osnovne trigonometrije u formule.

Još jedna profesija koja je nezamisliva bez trigonometrije je geodet. Koristeći teodolit i libelu ili složeniji uređaj - tahometar, ovi ljudi mjere visinsku razliku između različitih tačaka na površini zemlje.

Ponovljivost

Trigonometrija se ne bavi samo uglovima i stranicama trougla, iako je tu počela svoje postojanje. U svim oblastima u kojima je prisutna cikličnost (biologija, medicina, fizika, muzika, itd.) naići ćete na graf čije ime vam je vjerovatno poznato - ovo je sinusni talas.

Takav graf je krug koji se odvija duž vremenske ose i izgleda kao val. Ako ste ikada radili sa osciloskopom na času fizike, znate o čemu govorimo. I muzički ekvilajzer i mjerač otkucaja srca koriste trigonometrijske formule u svom radu.

Konačno

Kada razmišljaju o tome kako naučiti trigonometriju, većina učenika srednjih i srednjih škola to počinje smatrati teškom i nepraktičnom naukom, jer se upoznaju samo sa dosadnim informacijama iz udžbenika.

Što se tiče nepraktičnosti, već smo vidjeli da je, u jednom ili drugom stepenu, sposobnost rukovanja sinusima i tangentima potrebna u gotovo svakom području aktivnosti. Što se tiče kompleksnosti... Razmislite: ako su ljudi koristili ovo znanje prije više od dvije hiljade godina, kada je odrasla osoba imala manje znanja od današnjeg srednjoškolca, da li je za vas lično realno da ovu oblast nauke izučavate na osnovnom nivou? Nekoliko sati promišljene vježbe rješavanja problema - i postići ćete svoj cilj proučavanjem osnovnog kursa, takozvane trigonometrije za lutke.