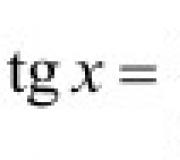Triqonometriya sadə və aydındır. Triqonometriya Triqonometrik funksiyalar izah olunur

Triqonometrik çevirmələri həyata keçirərkən bu ipuçlarına əməl edin:

1. Məsələnin başdan sona həllini dərhal tapmağa çalışmayın.
2. Bütün nümunəni bir anda çevirməyə çalışmayın. İrəli kiçik addımlar atın.
3. Unutmayın ki, triqonometriyada triqonometrik düsturlara əlavə olaraq, siz hələ də bütün ədalətli cəbri çevrilmələrdən (mötərizə, kəsrlərin qısaldılması, qısaldılmış vurma düsturları və s.) istifadə edə bilərsiniz.
4. Hər şeyin yaxşı olacağına inanın.

Əsas triqonometrik düsturlar

Triqonometriyada əksər düsturlar tez-tez həm sağdan sola, həm də soldan sağa istifadə olunur, ona görə də siz bu düsturları o qədər yaxşı öyrənməlisiniz ki, bəzi düsturları hər iki istiqamətdə asanlıqla tətbiq edə biləsiniz. Əvvəlcə triqonometrik funksiyaların təriflərini yazaq. Düzgün üçbucaq olsun:

Sonra sinusun tərifi:

Kosinusun tərifi:

Tangens tərifi:

Kotangensin tərifi:

Əsas triqonometrik eynilik:

Əsas triqonometrik eynilikdən ən sadə nəticələr:

İkiqat bucaq düsturları.İkiqat bucaq sinüsü:

İkiqat bucağın kosinusu:

İkiqat bucağın tangensi:

İkiqat bucağın kotangensi:

Əlavə triqonometrik düsturlar

Triqonometrik əlavə düsturları. Cəminin sinusu:

Fərqin sinusu:

Cəminin kosinusu:

Fərqin kosinusu:

Cəmin tangensi:

Fərq tangensi:

Məbləğin kotangenti:

Fərqin kotangensi:

Cəmi məhsula çevirmək üçün triqonometrik düsturlar. Sinusların cəmi:

Sinus fərqi:

Kosinusların cəmi:

Kosinusların fərqi:

Tangenslərin cəmi:

Tangens fərqi:

Kotangentlərin cəmi:

Kotangent fərqi:

Məhsulu cəmiyə çevirmək üçün triqonometrik düsturlar. Sinusların məhsulu:

Sinus və kosinusun hasilatı:

Kosinusların məhsulu:

Dərəcə azaldılması düsturları.

Yarım bucaq düsturları.

Triqonometrik azalma düsturları

Kosinus funksiyası deyilir kofunksiya sinus funksiyaları və əksinə. Eynilə, tangens və kotangent funksiyalar kofunksiyalardır. Azaltma düsturları aşağıdakı qaydada tərtib edilə bilər:

• Əgər kiçilmə düsturunda 90 dərəcədən və ya 270 dərəcədən bucaq çıxılırsa (əlavə olunur), onda azaldılmış funksiya kofunksiyaya çevrilir;
• Əgər kiçilmə düsturunda bucaq 180 dərəcədən və ya 360 dərəcədən çıxılırsa (əlavə olunur), onda azaldılmış funksiyanın adı saxlanılır;
• Bu halda, çıxarılan (əlavə edilmiş) bucağı iti hesab etsək, azaldılmış (yəni orijinal) funksiyanın müvafiq kvadrantda olması işarəsi azaldılmış funksiyanın qarşısında qoyulur.

Azaltma düsturları cədvəl şəklində verilmişdir:

By triqonometrik dairə triqonometrik funksiyaların cədvəl qiymətlərini təyin etmək asandır:

Triqonometrik tənliklər

Müəyyən bir triqonometrik tənliyi həll etmək üçün onu aşağıda müzakirə ediləcək ən sadə triqonometrik tənliklərdən birinə endirmək lazımdır. Bunun üçün:

• Yuxarıda verilmiş triqonometrik düsturlardan istifadə edə bilərsiniz. Eyni zamanda, bütün nümunəni bir anda dəyişdirməyə çalışmaq lazım deyil, ancaq kiçik addımlarla irəliləmək lazımdır.
• Cəbri üsullardan istifadə edərək bəzi ifadələrin çevrilməsinin mümkünlüyünü unutmamalıyıq, yəni. məsələn, mötərizədə nəyisə çıxarmaq və ya əksinə, mötərizələri açmaq, kəsri azaltmaq, qısaldılmış vurma düsturu tətbiq etmək, kəsrləri ortaq məxrəcə gətirmək və s.
• Triqonometrik tənlikləri həll edərkən istifadə edə bilərsiniz qruplaşdırma üsulu. Yadda saxlamaq lazımdır ki, bir neçə amilin hasilinin sıfıra bərabər olması üçün onlardan hər hansı birinin sıfıra bərabər olması kifayətdir və qalanları var idi.
• Müraciət edir dəyişən əvəzetmə üsulu, həmişə olduğu kimi, dəyişdirmə tətbiq edildikdən sonra tənlik daha sadə olmalıdır və orijinal dəyişəni ehtiva etməməlidir. Siz həmçinin tərs dəyişdirmə həyata keçirməyi unutmayın.
• Unutmayın ki, homojen tənliklər tez-tez triqonometriyada görünür.
• Modulları açarkən və ya triqonometrik funksiyaları olan irrasional tənlikləri həll edərkən, adi funksiyalarla uyğun tənliklərin həllinin bütün incəliklərini xatırlamalı və nəzərə almalısınız.
• ODZ-ni xatırlayın (triqonometrik tənliklərdə ODZ-də məhdudiyyətlər əsasən sıfıra bölünə bilməyəcəyinizdən irəli gəlir, lakin digər məhdudiyyətləri, xüsusən də rasional güclərdə və hətta güclərin kökləri altındakı ifadələrin müsbətliyini unutma). Həm də unutmayın ki, sinus və kosinus dəyərləri yalnız mənfi birdən artı birə qədər olan diapazonda ola bilər.

Əsas odur ki, nə edəcəyinizi bilmirsinizsə, heç olmasa bir şey edin və əsas odur ki, triqonometrik düsturlardan düzgün istifadə edin. Əldə etdiyiniz şey getdikcə yaxşılaşırsa, həll yoluna davam edin və daha da pisləşirsə, əvvələ qayıdın və başqa düsturları tətbiq etməyə çalışın, düzgün həll tapana qədər bunu edin.

Ən sadə triqonometrik tənliklərin həlli üçün düsturlar. Sinus üçün həlli yazmağın iki ekvivalent forması var:

Digər triqonometrik funksiyalar üçün qeyd birmənalı deyil. Kosinus üçün:

Tangens üçün:

Kotangent üçün:

Bəzi xüsusi hallarda triqonometrik tənliklərin həlli:

Bu üç nöqtənin müvəffəqiyyətli, çalışqan və məsuliyyətli şəkildə həyata keçirilməsi sizə KT-də mükəmməl nəticə göstərməyə imkan verəcək, maksimum bacardıqlarınızdır.

Səhv tapdınız?

Təlim materiallarında səhv tapdığınızı düşünürsünüzsə, bu barədə e-poçt vasitəsilə yazın. Siz həmçinin sosial şəbəkədə xəta barədə məlumat verə bilərsiniz (). Məktubda mövzunu (fizika və ya riyaziyyat), mövzunun və ya testin adını və ya nömrəsini, problemin nömrəsini və ya mətndə (səhifədə) sizin fikrinizcə səhv olan yeri göstərin. Həmçinin şübhəli səhvin nə olduğunu təsvir edin. Məktubunuz diqqətdən kənarda qalmayacaq, səhv ya düzəldiləcək, ya da niyə səhv olmadığı sizə izah ediləcək.

Məxfiliyinizi qorumaq bizim üçün vacibdir. Bu səbəbdən biz sizin məlumatlarınızı necə istifadə etdiyimizi və saxladığımızı təsvir edən Məxfilik Siyasəti hazırlamışıq. Zəhmət olmasa məxfilik təcrübələrimizi nəzərdən keçirin və hər hansı sualınız olarsa, bizə bildirin.

Şəxsi məlumatların toplanması və istifadəsi

Şəxsi məlumat müəyyən bir şəxsi müəyyən etmək və ya əlaqə saxlamaq üçün istifadə edilə bilən məlumatlara aiddir.

İstənilən vaxt bizimlə əlaqə saxladığınız zaman sizdən şəxsi məlumatlarınızı təqdim etməyiniz tələb oluna bilər.

Aşağıda toplaya biləcəyimiz şəxsi məlumat növlərinə və bu cür məlumatlardan necə istifadə edə biləcəyimizə dair bəzi nümunələr verilmişdir.

Hansı şəxsi məlumatları toplayırıq:

• Saytda ərizə təqdim etdiyiniz zaman biz müxtəlif məlumatlar, o cümlədən adınız, telefon nömrəniz, e-poçt ünvanınız və s.

Şəxsi məlumatlarınızı necə istifadə edirik:

• Topladığımız şəxsi məlumatlar bizə unikal təkliflər, promosyonlar və digər tədbirlər və qarşıdan gələn tədbirlərlə bağlı sizinlə əlaqə saxlamağa imkan verir.
• Zaman-zaman biz sizin şəxsi məlumatlarınızdan vacib bildirişlər və kommunikasiyalar göndərmək üçün istifadə edə bilərik.
• Təqdim etdiyimiz xidmətləri təkmilləşdirmək və sizə xidmətlərimizlə bağlı tövsiyələr vermək üçün auditlərin aparılması, məlumatların təhlili və müxtəlif tədqiqatların aparılması kimi şəxsi məlumatlardan daxili məqsədlər üçün də istifadə edə bilərik.
• Əgər siz uduş tirajında, müsabiqədə və ya oxşar təşviqatda iştirak edirsinizsə, biz bu cür proqramları idarə etmək üçün təqdim etdiyiniz məlumatdan istifadə edə bilərik.

Üçüncü tərəflərə məlumatların açıqlanması

Sizdən alınan məlumatları üçüncü şəxslərə açıqlamırıq.

İstisnalar:

• Zəruri hallarda - qanuna uyğun olaraq, məhkəmə qaydasında, məhkəmə prosesində və/və ya ictimai sorğular və ya Rusiya Federasiyasının dövlət orqanlarının sorğuları əsasında - şəxsi məlumatlarınızı açıqlamaq. Bu cür açıqlamanın təhlükəsizlik, hüquq-mühafizə və ya digər ictimai əhəmiyyətli məqsədlər üçün zəruri və ya uyğun olduğunu müəyyən etsək, sizinlə bağlı məlumatları da açıqlaya bilərik.
• Yenidən təşkil etmə, birləşmə və ya satış halında, biz topladığımız şəxsi məlumatları müvafiq varis üçüncü tərəfə ötürə bilərik.

Şəxsi məlumatların qorunması

Biz şəxsi məlumatlarınızı itkidən, oğurluqdan və sui-istifadədən, habelə icazəsiz daxil olmaqdan, açıqlamadan, dəyişdirilməkdən və məhv olmaqdan qorumaq üçün inzibati, texniki və fiziki tədbirləri görürük.

Şirkət səviyyəsində məxfiliyinizə hörmət etmək

Şəxsi məlumatlarınızın təhlükəsiz olmasını təmin etmək üçün biz əməkdaşlarımıza məxfilik və təhlükəsizlik standartlarını çatdırırıq və məxfilik təcrübələrini ciddi şəkildə tətbiq edirik.

Bu dərsdə biz tərifləri öyrənəcəyik triqonometrik funksiyalar və onların əsas xassələri, ilə işləməyi öyrənin triqonometrik dairə, gəlin bunun nə olduğunu öyrənək funksiyanın müddəti və müxtəlifləri xatırlayın bucaqların ölçülməsi üsulları. Bundan əlavə, istifadəni başa düşəcəyik azaldılması düsturları.

Bu dərs sizə tapşırıq növlərindən birinə hazırlaşmağa kömək edəcək AT 7.

Riyaziyyatdan Vahid Dövlət İmtahanına hazırlıq

Təcrübə

Dərs 7.Triqonometriyaya giriş.

Nəzəriyyə

Dərsin xülasəsi

Bu gün biz çoxları üçün qorxulu adı olan “Triqonometriya” bölməsinə başlayırıq. Dərhal aydınlaşdıraq ki, bu, bəzilərinin düşündüyü kimi, adı ilə həndəsəyə oxşar ayrıca bir mövzu deyil. Yunan dilindən tərcümə edilmiş "triqonometriya" sözü "üçbucaqların ölçülməsi" deməkdir və həndəsə ilə birbaşa bağlıdır. Bundan əlavə, triqonometrik hesablamalar fizika və texnologiyada geniş istifadə olunur. Ancaq biz əsas triqonometrik funksiyaların düzbucaqlı üçbucaqdan istifadə edərək həndəsəyə necə daxil edildiyini nəzərdən keçirəcəyik.

Biz indicə "triqonometrik funksiya" terminindən istifadə etdik - bu o deməkdir ki, biz bir dəyişən ilə digəri arasında müəyyən uyğunluq qanunlarının bütün sinfini təqdim edəcəyik.

Bunu etmək üçün, şəkildə görə biləcəyiniz rahatlıq üçün tərəflər və bucaqlar üçün standart qeydlərdən istifadə olunan düzbucaqlı üçbucağı nəzərdən keçirin:

Məsələn, bucağı nəzərdən keçirəkvə bunun üçün aşağıdakı hərəkətləri daxil edin:

Qarşı tərəfin hipotenuz sinusuna nisbətini adlandıraq, yəni.

Qonşu ayağın hipotenuz kosinusuna nisbətini adlandıraq, yəni. ;

Qarşı tərəfin bitişik tərəfə nisbəti tangens adlanacaq, yəni. ;

Qonşu tərəfin qarşı tərəfə nisbəti kotangent adlanacaq, yəni. .

Bucaq ilə bütün bu hərəkətlər deyilir triqonometrik funksiyalar. Bucağın özü adətən adlanır triqonometrik funksiyanın arqumenti və o, məsələn, cəbrdə adət olduğu kimi, X ilə işarələnə bilər.

Dərhal başa düşmək lazımdır ki, triqonometrik funksiyalar xüsusi olaraq düzbucaqlı üçbucağın tərəflərindən deyil, bucaqdan asılıdır. Tərəflərin uzunluqları fərqli olacaq, lakin tərəflərin bütün bucaqları və nisbətləri dəyişməyəcək, buna bənzər bir üçbucağı nəzərdən keçirsək, bunu sübut etmək asandır, yəni. Bucaqların triqonometrik funksiyaları da dəyişməz qalacaq.

Triqonometrik funksiyaların bu tərifindən sonra sual yarana bilər: “Orada, məsələn,? Axı, küncdüzbucaqlı üçbucaqda ola bilməz» . Qəribədir ki, bu sualın cavabı müsbətdir və bu ifadənin dəyəri bərabərdir və bu daha da təəccüblüdür, çünki bütün triqonometrik funksiyalar düzbucaqlı üçbucağın tərəflərinin nisbətidir və tərəflərin uzunluqları müsbət ədədlər.

Amma bunda heç bir paradoks yoxdur. Məsələ burasındadır ki, məsələn, fizikada bəzi prosesləri təsvir edərkən bucaqların təkcə böyük deyil, həm də böyük və hətta triqonometrik funksiyalarından istifadə etmək lazımdır. Bunu etmək üçün, sözdə istifadə edərək triqonometrik funksiyaların hesablanması üçün daha ümumi bir qayda tətbiq etmək lazımdır. "vahid triqonometrik dairə".

Bu, mərkəzi Kartezyen müstəvisinin başlanğıcında olması üçün çəkilmiş vahid radiuslu bir dairədir.

Bu dairədə bucaqları təsvir etmək üçün onları haradan yerləşdirmək barədə razılaşmaq lazımdır. Bucaq istinad şüası kimi absis oxunun müsbət istiqamətini qəbul etmək qəbul edilir, yəni. x oxu. Bucaqların çökmə istiqaməti saat yönünün əksinə hesab olunur. Bu razılaşmalara əsaslanaraq, əvvəlcə iti bucağı bir kənara qoyaq. Məhz belə kəskin bucaqlar üçün düz üçbucaqda triqonometrik funksiyaların qiymətlərini necə hesablayacağımızı artıq bilirik. Belə çıxır ki, təsvir edilmiş dairədən istifadə edərək triqonometrik funksiyaları da hesablaya bilərsiniz, yalnız daha rahatdır.

Kəskin bucağın sinusunun və kosinusunun dəyərləri bu bucağın tərəfinin vahid dairə ilə kəsişmə nöqtəsinin koordinatlarıdır:

Bunu belə yazmaq olar:

:

Buna əsaslanaraq x oxu boyunca koordinatlar kosinusun qiymətini, y oxu boyunca koordinatlar isə bucağın sinusunun qiymətini göstərir., şəkildə gördüyünüz kimi vahid dairə ilə koordinat sistemindəki oxların adlarını dəyişdirmək rahatdır:

Absis oxunun adı kosinus oxuna, ordinat oxunun isə sinus oxuna dəyişdirilir.

Sinus və kosinusu təyin etmək üçün göstərilən qayda həm küt bucaqlar, həm də ilə arasında olan bucaqlar üçün ümumiləşdirilmişdir. Bu halda sinuslar və kosinuslar həm müsbət, həm də mənfi dəyərləri qəbul edə bilər. Müxtəlif bu triqonometrik funksiyaların qiymətlərinin əlamətləri Sözügedən bucağın hansı dörddəbirə düşdüyündən asılı olaraq, onu aşağıdakı kimi təsvir etmək adətdir:

Gördüyünüz kimi, triqonometrik funksiyaların əlamətləri onlara uyğun oxların müsbət və mənfi istiqamətləri ilə müəyyən edilir.

Bundan əlavə, bir məqama diqqət yetirmək lazımdır ki, vahid çevrədəki nöqtənin həm absis, həm də ordinat oxu boyunca ən böyük koordinatı birə bərabərdir, ən kiçik isə mənfi birdir, onda sinus və kosinus dəyərləri bu nömrələrlə məhdudlaşır:

Bu qeydlər də adətən bu formada yazılır:

Triqonometrik çevrəyə tangens və kotangens funksiyalarını təqdim etmək üçün əlavə elementlər çəkmək lazımdır: A nöqtəsində çevrəyə toxunan - ondan bucağın tangensinin qiyməti müəyyən edilir, atına olan tangens. B nöqtəsi - ondan bucağın kotangentinin qiyməti müəyyən edilir.

Bununla belə, biz triqonometrik çevrədəki tangens və kotangenslərin tərifini araşdırmayacağıq, çünki Onları necə edəcəyimizi bildiyimiz bir bucağın sinus və kosinusunun dəyərlərini bilməklə asanlıqla hesablamaq olar. Əgər siz triqonometrik dairədə tangens və kotangensin hesablanmasını öyrənməklə maraqlanırsınızsa, 10-cu sinif cəbr kursunun proqramı ilə tanış olun.

Biz yalnız dairədəki şəkli göstəririk tangens və kotangens əlamətləri bucaqdan asılı olaraq:

Qeyd edək ki, sinus və kosinus dəyərlərinin diapazonlarına bənzər olaraq, siz tangens və kotangens dəyərlərinin diapazonlarını təyin edə bilərsiniz. Onların triqonometrik dairədəki təriflərinə əsaslanaraq, bu funksiyaların mənaları məhdud deyil:

Bu kimi başqa nə yazmaq olar:

-dən aralığında olan bucaqlara əlavə olaraq, triqonometrik dairə daha böyük və hətta mənfi bucaqlarla işləməyə imkan verir. Belə bucaq qiymətləri həndəsə üçün mənasız görünsə də, müəyyən fiziki prosesləri təsvir etmək üçün istifadə olunur. Məsələn, suala necə cavab verirsiniz: "Saat əqrəbi bir gündə hansı bucaqla dönəcək?" Bu müddət ərzində o, iki tam inqilabı tamamlayacaq və bir inqilabda keçəcək, yəni. bir gün ərzində çevriləcək. Gördüyünüz kimi, bu cür dəyərlər çox praktik məna daşıyır. Bucaq işarələri fırlanma istiqamətini göstərmək üçün istifadə olunur - istiqamətlərdən birinin müsbət açılarla, digəri isə mənfi olanlarla ölçülməsi razılaşdırılır. Bunu triqonometrik dairədə necə nəzərə almaq olar?

Belə bucaqları olan bir dairədə onlar aşağıdakı kimi işləyirlər:

1) -dən böyük olan bucaqlar saat əqrəbinin əksi istiqamətində çəkilir, başlanğıcdan lazım olan qədər çox dəfə keçir. Məsələn, bir bucaq qurmaq üçün iki tam inqilabdan və digərindən keçmək lazımdır. Bütün triqonometrik funksiyalar son mövqe üçün hesablanır. Üçün və üçün bütün triqonometrik funksiyaların qiymətlərinin eyni olacağını görmək asandır.

2) Mənfi bucaqlar müsbət olanlarla eyni prinsipə uyğun olaraq, yalnız saat yönünün əksinə yerləşdirilir.

Yalnız böyük bucaqların qurulması üsulu ilə, bir-birindən fərqlənən bucaqların sinuslarının və kosinuslarının qiymətlərinin eyni olduğu qənaətinə gələ bilərik. Tangens və kotangenslərin qiymətlərini təhlil etsək, onlar ilə fərqlənən bucaqlar üçün eyni olacaqdır.

Arqumentə əlavə olunduqda funksiyanın dəyərini dəyişməyən belə minimal sıfırdan fərqli ədədlər adlanır. dövr bu funksiya.

Beləliklə, dövrsinus və kosinus bərabərdir, və tangens və kotangens. Bu o deməkdir ki, bu dövrləri nəzərdən keçirilən bucaqlardan nə qədər əlavə və ya çıxarsanız da, triqonometrik funksiyaların qiymətləri dəyişməyəcək.

Misal üçün, , və s.

Triqonometrik funksiyaların bu xassəsinin daha ətraflı izahına və tətbiqinə daha sonra qayıdacağıq.

Eyni arqumentin triqonometrik funksiyaları arasında çox tez-tez istifadə olunan və çağırılan müəyyən əlaqələr var əsas triqonometrik eyniliklər.

Onlar belə görünür:

1) , sözdə "triqonometrik vahid"

3)

4)

5)

Qeyd edək ki, məsələn, qeyd bütün triqonometrik funksiyanın kvadrat olduğunu bildirir. Bunlar. bu formada təmsil oluna bilər: . Bunun kimi qeydlərə bərabər olmadığını başa düşmək vacibdir, bu halda bütün funksiya deyil, yalnız arqument kvadratlaşdırılır və bundan əlavə, bu tip ifadələr olduqca nadirdir.

Bir çox növ problemlərin həllində faydalı ola biləcək birinci şəxsiyyətdən iki çox faydalı nəticə var. Sadə çevrilmələrdən sonra sinusu eyni bucağın kosinusu ilə və əksinə ifadə edə bilərsiniz:

İki mümkün ifadə işarəsi görünür, çünki arifmetik kvadrat kökün götürülməsi yalnız mənfi olmayan qiymətlər verir, sinus və kosinus isə artıq gördüyümüz kimi mənfi qiymətlərə malik ola bilər. Üstəlik, bu funksiyaların əlamətlərini triqonometrik dairədən istifadə edərək, onlarda hansı açıların mövcudluğundan asılı olaraq təyin etmək ən əlverişlidir.

İndi xatırlayaq ki, bucaqlar iki şəkildə ölçülə bilər: dərəcə və radyan. Bir dərəcə və bir radanın təriflərini göstərək.

Bir dərəcə- dairəyə bərabər bir qövsdən keçən iki radiusun yaratdığı bucaqdır.

Bir radian- bu, uzunluğu radiuslara bərabər olan bir qövsün altındakı iki radiusun yaratdığı bucaqdır.

Bunlar. onlar tamamilə bərabər olan bucaqların ölçülməsinin iki fərqli üsuludur. Triqonometrik funksiyalarla xarakterizə olunan fiziki prosesləri təsvir edərkən, bucaqların radian ölçüsündən istifadə etmək adətdir, buna görə də buna öyrəşməli olacağıq.

Radianlarda bucaqları pi fraksiyalarında ölçmək adətdir, məsələn, və ya. Bu halda, 3.14-ə bərabər olan "pi" rəqəminin dəyəri əvəz edilə bilər, lakin bu nadir hallarda edilir.

Bucaqların dərəcə ölçüsünü radana çevirmək üçün bucağın olması faktından istifadə edin, ondan ümumi tərcümə düsturu əldə etmək asandır:

Məsələn, radianlara çevirək: .

Bunun əksi də var düsturradyandan dərəcəyə çevrilmə:

Məsələn, dərəcələrə çevirək: .

Bu mövzuda radian bucağın ölçüsündən tez-tez istifadə edəcəyik.

İndi müxtəlif bucaqların triqonometrik funksiyaları ilə hansı xüsusi dəyərlərin verilə biləcəyini xatırlamaq vaxtıdır. -nin çoxluğu olan bəzi bucaqlar üçün var triqonometrik funksiyaların qiymətləri cədvəli. Rahatlıq üçün bucaqlar dərəcə və radian ölçüləri ilə verilir.

Bu açılar bir çox problemlərdə tez-tez rast gəlinir və bu cədvəldə inamla hərəkət edə bilmək məsləhətdir. Bəzi bucaqların tangens və kotangens dəyərlərinin mənası yoxdur, bu da cədvəldə tire kimi göstərilir. Bunun niyə belə olduğunu özünüz düşünün və ya bunu dərs üçün əlavədə daha ətraflı oxuyun.

İlk triqonometriya dərsimizdə tanış olmağımız lazım olan son şeydir azalma düsturlarından istifadə edərək triqonometrik funksiyaların çevrilməsi.

Belə çıxır ki, triqonometrik funksiyalar üçün kifayət qədər ümumi və rahat şəkildə sadələşdirilmiş müəyyən bir ifadə növü var. Məsələn, bunlar ifadələrdir: və s.

Bunlar. Arqument kimi ixtiyari bucağı götürən, tam və ya yarım hissəyə dəyişdirilən funksiyalar haqqında danışacağıq. Bu cür funksiyalar hissələrin ixtiyari əlavə və ya çıxma bucağına bərabər olan arqumentə qədər sadələşdirilir. Misal üçün, , A . Göründüyü kimi, nəticə əks funksiya ola bilər və funksiya işarəni dəyişə bilər.

Buna görə də bu cür funksiyaların transformasiyası qaydalarını iki mərhələyə bölmək olar. Əvvəlcə transformasiyadan sonra hansı funksiyanı əldə edəcəyinizi müəyyənləşdirməlisiniz:

1) Əgər ixtiyari arqument tam ədədə dəyişdirilirsə, funksiya dəyişmir. Bu, tipli funksiyalar üçün doğrudur, burada istənilən tam ədəd;

Bir vaxtlar məktəbdə triqonometriyanın öyrənilməsi üçün ayrıca kurs var idi. Sertifikat üç riyaziyyat fənni üzrə qiymətləri ehtiva edirdi: cəbr, həndəsə və triqonometriya.

Sonra məktəb təhsili islahatının bir hissəsi olaraq triqonometriya ayrıca bir fənn kimi mövcud olmağı dayandırdı. Müasir məktəbdə triqonometriya ilə ilk tanışlıq 8-ci sinif həndəsə kursunda baş verir. 10-cu sinif cəbr kursunda fənnin daha dərindən öyrənilməsi davam edir.

Sinus, kosinus, tangens və kotangensin tərifləri əvvəlcə düzbucaqlı üçbucağın tərəflərinin əlaqəsi vasitəsilə həndəsədə verilir.

Düzbucaqlı üçbucaqdakı iti bucaq qarşı tərəfin hipotenuzaya nisbətidir.

Kosinus Düzbucaqlı üçbucaqda kəskin bucaq qonşu ayağın hipotenuzaya nisbətidir.

Tangens Düzbucaqlı üçbucaqda kəskin bucaq qarşı tərəfin bitişik tərəfə nisbətidir.

Kotangent Düzbucaqlı üçbucaqda iti bucaq qonşu tərəfin qarşı tərəfə nisbətidir.

Bu təriflər yalnız kəskin açılara aiddir (0º - 90°).

Misal üçün,

ABC üçbucağında, burada ∠C=90°, BC A bucağına əks ayaq, AC A bucağına bitişik ayaq, AB hipotenuzdur.

10-cu sinif cəbr kursu istənilən bucaq (o cümlədən mənfi) üçün sinus, kosinus, tangens və kotangensin təriflərini təqdim edir.

Mərkəzi başlanğıcda - O(0;0) nöqtəsində olan R radiuslu dairəni nəzərdən keçirək. Dairənin absis oxunun müsbət istiqaməti ilə kəsişmə nöqtəsini P 0 kimi qeyd edək.

Həndəsədə bucaq iki şüa ilə məhdudlaşan müstəvi hissəsi kimi qəbul edilir. Bu təriflə bucaq 0° ilə 180° arasında dəyişir.

Triqonometriyada bucaq OP 0 şüasının başlanğıc O nöqtəsi ətrafında fırlanmasının nəticəsi hesab edilir.

Eyni zamanda, onlar şüanın müsbət hərəkət istiqaməti kimi saat əqrəbinin əksi istiqamətində, mənfi isə saat əqrəbinin əksinə (bu razılaşma Günəşin Yer ətrafında həqiqi hərəkəti ilə bağlıdır) hesab etmək barədə razılığa gəliblər.

Məsələn, OP 0 şüası O nöqtəsi ətrafında saat əqrəbinin əksinə α bucağı ilə fırlananda P 0 nöqtəsi P α nöqtəsinə gedəcək,

saat əqrəbi istiqamətində α bucağı ilə dönərkən - F nöqtəsinə.

Bu təriflə bucaq istənilən qiymət ala bilər.

OP 0 şüasını saat əqrəbinin əksinə döndərməyə davam etsək, α°+360°, α°+360°·2,...,α°+360°·n bucağından dönərkən, burada n tam ədəddir (n∈). Ζ), yenə P α nöqtəsinə keçək:

Bucaqlar dərəcə və radyanla ölçülür.

1°, işlənmiş bucağın dərəcə ölçüsünün 1/180-ə bərabər olan bir açıdır.

1 radian, qövs uzunluğu dairənin radiusuna bərabər olan mərkəzi bucaqdır:

∠AOB=1 rad.

Radian simvolları adətən yazılmır. Dərəcə təyinatı qeyddən çıxarıla bilməz.

Misal üçün,

OP 0 şüasının O nöqtəsi ətrafında saat əqrəbinin əksinə α bucağı ilə fırlanması ilə P 0 nöqtəsindən alınan P α nöqtəsi P α (x;y) koordinatlarına malikdir.

P α nöqtəsindən absis oxuna perpendikulyar P α A salaq.

OP α A düzbucaqlı üçbucağında:

P α A - α bucağına qarşı ayaq,

OA - α bucağına bitişik ayaq,

OP α hipotenuzdur.

P α A=y, OA=x, OP α =R.

Düzbucaqlı üçbucaqda sinus, kosinus, tangens və kotangensin tərifinə görə:

Beləliklə, ixtiyari radiusun başlanğıcında mərkəzi olan bir dairə vəziyyətində sinusα bucağı P α nöqtəsinin ordinatının radiusun uzunluğuna nisbətidir.

Kosinus bucaq α P α nöqtəsinin absisinin radiusun uzunluğuna nisbətidir.

Tangensα bucağı P α nöqtəsinin ordinatının onun absissinə nisbətidir.

Kotangentα bucağı P α nöqtəsinin absissinin onun ordinatına nisbətidir.

Sinus, kosinus, tangens və kotangensin dəyərləri yalnız α dəyərindən asılıdır və R radiusunun uzunluğundan asılı deyildir (bu, dairələrin oxşarlığından irəli gəlir).

Buna görə də R=1 seçmək rahatdır.

Başında mərkəzi və radiusu R=1 olan çevrə vahid çevrə adlanır.

Təriflər

1) Sinusα bucağı vahid dairənin P α (x;y) nöqtəsinin ordinatı adlanır:

2) Kosinusα bucağı vahid çevrənin P α (x;y) nöqtəsinin absisi adlanır:

3) Tangensα bucağı P α (x;y) nöqtəsinin ordinatının onun absissinə nisbətidir, yəni sinα ilə kosα nisbətidir (burada cosα≠0):

4) Kotangentα bucağı P α (x;y) nöqtəsinin absissinin onun ordinatına nisbəti, yəni kosα ilə sinα nisbətidir (burada sinα≠0):

Bu şəkildə təqdim edilən təriflər bizə yalnız bucaqların triqonometrik funksiyalarını deyil, həm də ədədi arqumentlərin triqonometrik funksiyalarını da nəzərdən keçirməyə imkan verir (əgər sinα, cosα, tanα və ctgα-nı α radyanlarında bir bucağın müvafiq triqonometrik funksiyaları kimi nəzərə alsaq, yəni α ədədinin sinusu α radyanla bucağın sinusu, α ədədinin kosinusu α radyanla bucağın kosinusudur və s.).

Triqonometrik funksiyaların xassələri 10 və ya 11-ci siniflərdə cəbr kursunda ayrıca mövzu kimi öyrənilir. Triqonometrik funksiyalar fizikada geniş istifadə olunur.

Sinus, kosinus, tangens - bu sözləri orta məktəb şagirdlərinin yanında tələffüz edərkən əmin ola bilərsiniz ki, onların üçdə ikisi sonrakı söhbətə marağını itirəcək. Səbəb ondan ibarətdir ki, məktəbdə triqonometriyanın əsasları reallıqdan tam təcrid olunmuş şəkildə öyrədilir və buna görə də şagirdlər düstur və teoremləri öyrənməyin mənasını görmürlər.

Əslində, daha yaxından araşdırıldıqda, bu bilik sahəsi çox maraqlıdır, həm də tətbiq olunur - triqonometriya astronomiya, tikinti, fizika, musiqi və bir çox başqa sahələrdə istifadə olunur.

Gəlin əsas anlayışlarla tanış olaq və riyaziyyat elminin bu sahəsini öyrənmək üçün bir neçə səbəbi sadalayaq.

Hekayə

Bəşəriyyətin gələcək triqonometriyanı sıfırdan yaratmağa nə zaman başladığı məlum deyil. Bununla belə, sənədləşdirilmişdir ki, artıq eramızdan əvvəl ikinci minillikdə misirlilər bu elmin əsasları ilə tanış idilər: arxeoloqlar bir tapşırığı olan bir papirus tapdılar, burada piramidanın iki məlum tərəfdəki meyl bucağını tapmaq tələb olunurdu.

Qədim Babil alimləri daha ciddi uğurlara imza atdılar. Əsrlər boyu astronomiyanı öyrənərək bir sıra teoremləri mənimsədilər, bucaqların ölçülməsi üçün xüsusi üsullar tətbiq etdilər, yeri gəlmişkən, bu gün istifadə edirik: dərəcələr, dəqiqələr və saniyələr Yunan-Roma mədəniyyətində Avropa elmi tərəfindən götürülmüşdür. bu birliklər babillilərdən gəldi.

Güman edilir ki, triqonometriyanın əsaslarına aid olan məşhur Pifaqor teoremi babillilərə təxminən dörd min il əvvəl məlum olub.

ad

Hərfi mənada "triqonometriya" termini "üçbucaqların ölçülməsi" kimi tərcümə edilə bilər. Uzun əsrlər boyu elmin bu bölməsində əsas tədqiqat obyekti düz üçbucaq, daha dəqiq desək, bucaqların böyüklükləri ilə onun tərəflərinin uzunluqları arasındakı əlaqə olmuşdur (bu gün triqonometriyanın sıfırdan öyrənilməsi bu bölmədən başlayır) . Həyatda tez-tez bir obyektin bütün tələb olunan parametrlərini (və ya obyektə olan məsafəni) ölçmək praktiki olaraq qeyri-mümkün olduqda və sonra hesablamalar vasitəsilə çatışmayan məlumatları əldə etmək zərurəti yarandıqda tez-tez vəziyyətlər olur.

Məsələn, keçmişdə insanlar kosmik obyektlərə olan məsafəni ölçə bilmirdilər, lakin bu məsafələri hesablamaq cəhdləri eramızın gəlişindən çox əvvəl baş verdi. Triqonometriya naviqasiyada da həlledici rol oynadı: bəzi biliklərə malik olan kapitan həmişə gecələr ulduzların yanında hərəkət edə və kursu tənzimləyə bilərdi.

Əsas anlayışlar

Triqonometriyanı sıfırdan mənimsəmək bir neçə əsas termini başa düşməyi və yadda saxlamağı tələb edir.

Müəyyən bir bucağın sinusu qarşı tərəfin hipotenuzaya nisbətidir. Aydınlaşdıraq ki, əks ayaq nəzərdə tutduğumuz bucağa qarşı uzanan tərəfdir. Beləliklə, əgər bucaq 30 dərəcədirsə, bu bucağın sinusu üçbucağın istənilən ölçüsü üçün həmişə ½-ə bərabər olacaqdır. Bucağın kosinusu bitişik ayağın hipotenuzaya nisbətidir.

Tangens qarşı tərəfin bitişik tərəfə nisbətidir (və ya eyni olan sinusun kosinusa nisbəti). Kotangent, tangensə bölünən vahiddir.

Bir vahid radiuslu dairənin uzunluğunun yarısı qədər olan məşhur Pi rəqəmini (3.14...) qeyd etmək lazımdır.

Populyar səhvlər

Triqonometriyanı sıfırdan öyrənən insanlar bir sıra səhvlərə yol verirlər - əsasən diqqətsizlik ucbatından.

Birincisi, həndəsə məsələlərini həll edərkən, sinusların və kosinusların istifadəsinin yalnız düz üçbucaqda mümkün olduğunu xatırlamalısınız. Belə olur ki, tələbə “avtomatik olaraq” üçbucağın ən uzun tərəfini hipotenuz kimi götürür və səhv hesablama nəticələri alır.

İkincisi, əvvəlcə seçilmiş bucaq üçün sinus və kosinus dəyərlərini qarışdırmaq asandır: xatırlayın ki, 30 dərəcə sinus ədədi olaraq 60 kosinusuna bərabərdir və əksinə. Yanlış rəqəmi əvəz etsəniz, bütün sonrakı hesablamalar səhv olacaq.

Üçüncüsü, problem tamamilə həll olunana qədər heç bir dəyəri yuvarlaqlaşdırmamalı, kökləri çıxarmamalı və ya ümumi kəsri onluq kimi yazmamalısınız. Çox vaxt tələbələr triqonometriya məsələsində "gözəl" rəqəm əldə etməyə çalışırlar və dərhal üçünün kökünü çıxarırlar, baxmayaraq ki, bir hərəkətdən sonra bu kök azaldıla bilər.

"Sine" sözünün etimologiyası

“Sine” sözünün tarixi həqiqətən qeyri-adidir. Fakt budur ki, bu sözün latın dilindən hərfi tərcüməsi "boş" deməkdir. Bunun səbəbi bir dildən digər dilə tərcümə zamanı sözün düzgün başa düşülməsinin itirilməsidir.

Əsas triqonometrik funksiyaların adları Hindistandan gəlir, burada sinus anlayışı Sanskrit dilində "simli" sözü ilə işarələnirdi - fakt budur ki, seqment dayandığı dairənin qövsü ilə birlikdə yay kimi görünürdü. . Ərəb sivilizasiyasının çiçəklənmə dövründə triqonometriya sahəsində Hindistan nailiyyətləri götürüldü və bu termin transkripsiya kimi ərəb dilinə keçdi. Elə oldu ki, bu dildə artıq depressiyanı bildirən oxşar söz var idi və ərəblər yerli sözlə alınma söz arasındakı fonetik fərqi başa düşdülərsə, elmi traktatları latın dilinə çevirən avropalılar səhvən heç bir mənası olmayan ərəb sözünü hərfi tərcümə etdilər. sinus anlayışı ilə etmək. Biz bu günə kimi istifadə edirik.

Dəyərlər cədvəli

Bütün mümkün bucaqların sinusları, kosinusları və tangensləri üçün ədədi dəyərləri ehtiva edən cədvəllər var. Aşağıda 0, 30, 45, 60 və 90 dərəcə bucaqlar üçün məlumatları təqdim edirik, xoşbəxtlikdən, onları xatırlamaq çox asandır.

Əgər bucağın sinusunun və ya kosinusunun ədədi dəyəri “başınızdan çıxıb”sa, onu özünüz çıxarmağın bir yolu var.

Həndəsi təmsil

Bir dairə çəkək və onun mərkəzindən absis və ordinat oxlarını çəkək. Absis oxu üfüqi, ordinat oxu şaqulidir. Onlar adətən müvafiq olaraq "X" və "Y" kimi imzalanır. İndi dairənin mərkəzindən elə bir düz xətt çəkəcəyik ki, onunla X oxu arasında bizə lazım olan bucaq alınsın. Nəhayət, düz xəttin dairəni kəsdiyi nöqtədən, X oxuna bir perpendikulyar düşürük, yaranan seqmentin uzunluğu bucağının sinusunun ədədi dəyərinə bərabər olacaqdır.

Tələb olunan dəyəri, məsələn, imtahan zamanı unutmusunuzsa və triqonometriya dərsliyiniz yoxdursa, bu üsul çox aktualdır. Bu şəkildə dəqiq bir rəqəm əldə etməyəcəksiniz, ancaq ½ və 1.73/2 (30 dərəcə bucaq sinus və kosinusu) arasındakı fərqi mütləq görəcəksiniz.

Ərizə

Triqonometriyadan istifadə edən ilk mütəxəssislərdən bəziləri açıq dənizdə başlarının üstündəki səmadan başqa istinad nöqtəsi olmayan dənizçilər idi. Bu gün gəmi kapitanları (təyyarələr və digər nəqliyyat növləri) ulduzlardan istifadə edərək ən qısa yolu axtarmırlar, lakin triqonometriyadan istifadə etmədən mümkün olmayan GPS naviqasiyasına fəal şəkildə müraciət edirlər.

Fizikanın demək olar ki, hər bir bölməsində sinus və kosinuslardan istifadə edərək hesablamalar tapa bilərsiniz: istər mexanikada gücün tətbiqi, kinematikada cisimlərin yolunun hesablanması, vibrasiya, dalğaların yayılması, işığın sınması - sadə triqonometriya olmadan edə bilməzsiniz. düsturlar.

Triqonometriyasız ağlasığmaz başqa bir peşə də yerölçəndir. Teodolit və səviyyə və ya daha mürəkkəb bir cihazdan - takometrdən istifadə edərək, bu insanlar yer səthinin müxtəlif nöqtələri arasındakı hündürlük fərqini ölçürlər.

Təkrarlanma qabiliyyəti

Triqonometriya yalnız üçbucağın bucaqları və tərəfləri ilə məşğul olmur, baxmayaraq ki, onun mövcudluğu burada başlamışdır. Tsiklliyin mövcud olduğu bütün sahələrdə (biologiya, tibb, fizika, musiqi və s.) Siz yəqin ki, adı sizə tanış olan qrafiklə qarşılaşacaqsınız - bu sinus dalğasıdır.

Belə bir qrafik zaman oxu boyunca açılmış dairədir və dalğaya bənzəyir. Əgər siz nə vaxtsa fizika dərsində osiloskopla işləmisinizsə, nədən danışdığımızı bilirsiniz. Həm musiqi ekvalayzeri, həm də ürək dərəcəsi monitoru öz işlərində triqonometriya düsturlarından istifadə edir.

Nəhayət

Triqonometriyanı necə öyrənmək barədə düşünərkən, orta və yuxarı sinif şagirdlərinin əksəriyyəti onu çətin və praktiki olmayan bir elm hesab etməyə başlayırlar, çünki onlar yalnız dərslikdən darıxdırıcı məlumatlarla tanış olurlar.

Praktikliyə gəlincə, biz artıq görmüşük ki, bu və ya digər dərəcədə, demək olar ki, istənilən fəaliyyət sahəsində sinus və tangensləri idarə etmək bacarığı tələb olunur. Mürəkkəbliyə gəlincə... Fikir verin: əgər insanlar iki min ildən çox əvvəl bu biliklərdən böyüklərin indiki orta məktəb şagirdindən daha az biliyə malik olduğu halda istifadə edirdilərsə, şəxsən sizin bu elm sahəsini baza səviyyədə öyrənmək realdırmı? Problemləri həll etmək üçün bir neçə saat düşünülmüş təcrübə - və siz dummies üçün triqonometriya deyilən əsas kursu öyrənməklə məqsədinizə çatacaqsınız.